GROUPWISE NON-RIGID IMAGE ALIGNMENT

Results of a Multiscale Iterative Best Edge Algorithm

Bernard Tiddeman

Department of Computer Science, Aberystwyth University, Aberystwyth, Wales, U.K.

David Hunter

School of Psychology, University of St Andrews, St Andrews, Scotland, U.K.

Keywords:

Groupwise image alignment, Congealing, Active appearance models.

Abstract:

In this paper we present an algorithm for groupwise image alignment using an iterative best edge point algo-

rithm. Neighbouring image edge points are matched for similarity in a two directional fashion. The matches

found are used to drive a regularised warp of the images into alignment. The algorithm works from low to

high resolution, with the matches calculated across the set ﬁrst at low resolution and towards progressively

ﬁner scales. The regularisation decreases across iterations, and the search area remains constant, so covers

larger effective area in the low resolution images. We also extend the method to 3D surfaces by combining the

2D image search with a 3D ICP algorithm. The results show that this gives a very efﬁcient algorithm that can

align many different sets of 2D images and 3D surfaces.

1 INTRODUCTION

Groupwise registration of images has received a great

deal of attention in recent years. Many applications

require the non-rigid alignment of different images

of the same class of object, such as medical images

or face images, for labelling of features or construc-

tion of morphable models such as active appearance

models (AAM) (Cootes et al., 2001). Models such

as AAM can be built using hand labelled examples,

but this is tedious and prone to error. Fully automatic

methods are therefore extremely valuable. Much of

the work performed in groupwise image alignment

thus far has followed the pattern:

• choose a suitable metric for image alignment,

• decide how to parameterise the non-rigid corre-

spondences, and

• use a non-linear optimisation routine to minimise

the chosen metric by altering the image parametri-

sations.

Where the database contains multiple object

classes this basic framework can be extended to in-

clude assignment of class labels (e.g. (Liu et al.,

2009)), although that is not the focus of this paper.

For the single class alignment problem various

metrics have been proposed. Rueckert et al (Rueck-

ert et al., 2003) used mutual information for pairwise

matching. Wang et al (Wang et al., 2010) used the

Jansen-Shannon divergence (JSD) of multi-scale im-

age information to estimate matches between 3D MRI

images. Z

ollei et al used a sum of voxel wise en-

tropies (Z

ollei et al., 2005). Davies originally pro-

posed the minimum description length (MDL) met-

ric for alignment of similar 2D outline shapes (Davies

et al., 2001), which has subsequently been extended to

3D surfaces and volumetric data (Davies et al., 2008)

and also images (Cootes et al., 2005) (Cootes et al.,

2010). The MDL approach, whilst theoretically ele-

gant is computationally expensive, requiring repeated

building of morphable models and the use of (usu-

ally relatively slow) non-linear optimisation routines.

Others have found good results can be achieved with

far simpler metrics, such as the error from the current

estimate of the mean (Cootes et al., 2010) (Sidorov

et al., 2009).

The image alignment metric often includes a

shape component. For MDL this is usually based on

the shape statistics of the training set. In other work

the shape constraints usually take the form of a reg-

ularisation term or restriction of the warps to sim-

ple smooth deformations. In practice these can of-

ten achieve better alignment than a statistical shape

model, which can become trapped in local minima

Tiddeman B. and Hunter D..

GROUPWISE NON-RIGID IMAGE ALIGNMENT - Results of a Multiscale Iterative Best Edge Algorithm.

DOI: 10.5220/0003326800220029

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 22-29

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b)

(e) (f)

Figure 1: Example output of our algorithm. (a), (c) and

(e) original blends without alignment, (b), (d) and (f) after

groupwise alignment on different images sets. (a-b) 434 im-

ages of men women and children of varying age and ethnic

origin, (c-d) 33 images of male faces from the IMM data set

and (e-f) 128 images from the FGNet Franck sequence.

(Cootes et al., 2010).

Parametrisation of the non-rigid registrations has

been achieved using a variety of methods, includ-

ing free form deformations (FFD) (e.g. (Rueckert

et al., 2003)) or piecewise afﬁne warps (e.g. (Cootes

et al., 2005) (Cootes et al., 2010) together with FFDs

for moving groups of control points). Sidorov et al

(Sidorov et al., 2009) showed how to combine multi-

ple piecewise afﬁne warps with arbitrary initial point

locations to create dense warping ﬁelds whilst keep-

ing the number of parameters to optimise over con-

stant across iterations.

Standard optimisation routines such as gradient

descent or the downhill simplex method can be

employed for minimising the error metric. Sev-

eral authors have elected to perform one-dimensional

searches along the current gradient direction (e.g.

(Cootes et al., 2005) (Wang et al., 2010). Sidorov et al

(Sidorov et al., 2009) used Simultaneous Perturbation

Stochastic Optimisation (SPSA) which can optimise

a function in approximately the same number of steps

as gradient descent, but using far fewer function eval-

uations (Spall, 1998). Their algorithm showed good

alignment but still required several hundred iterations

through the image set to achieve convergence.

An entirely different approach to non-rigid align-

ment is the iterative closest point algorithm which is

usually applied to 3D data sets. Both rigid and non-

rigid variation on the algorithm exist, it can be imple-

mented very efﬁciently and is guaranteed to converge

to a local minimum when one dataset is a subset of

another. Previous attempts have been made to com-

bine edge point matching into a groupwise alignment

algorithm. Hugnafel et al (Hufnagel et al., 2008) de-

veloped a groupwise expectation-maximisation ICP

algorithm for matching 3D surface shapes. Wang et

al (Wang et al., 2008) represented the points using

mixtures of Gaussians and iteratively minimised the

JSD. For image data Di et al (Di et al., 2007) devel-

oped a spatio-temporal generative model to automat-

ically align image sequences, but the algorithm was

not demonstrated on sets of independent images.

In this paper we develop a method for groupwise

image shape parametrisation and alignment based on

a multi-resolution ICP variant in which we ﬁnd the

best match of edge maxima in a local neighbour-

hood of the search point. The algorithm developed is

simple to implement, efﬁcient and shows promising

alignment results.

2 METHOD

In this section we ﬁrst give an overview of the group-

wise alignment algorithm and then describe parts of

the algorithm in more detail. Multi-resolution has

been used in previous work, but in this algorithm it

plays a crucial role in the matching. Very localised

searches are used for matching points in the low reso-

lution version of the problem, which brings the points

in higher resolutions sufﬁciently close for matching

using an equally localised search. All images are reg-

istered to the current estimate of the average at a low

resolution, then the average estimate is recalculated

and the process is repeated at the next higher resolu-

tion (Algorithm 1).

2.1 Point Selection and Matching

Starting at the lowest resolution, maxima of the local

image intensity are found (Mallet, 1989) (Canny,

GROUPWISE NON-RIGID IMAGE ALIGNMENT - Results of a Multiscale Iterative Best Edge Algorithm

Algorithm 1: Groupwise registration algorithm.

Require: Images {I

} = {I

,...,I

}

∀iΦ

= 1 {Initialise all warps to the identity}

r = 2

{initialise resolution parameter}

while r ≥ 1 do

A =

∑

i=1

(Φ

(x)) {Estimate average}

for i = 1 to N do

W = I

(Φ

(x)) {Warp current image}

φ = warpU pdate(A,W,r) {Get warp update,

Algorithm 2}

(x) = φ(Φ

(x)) {Compose warp update

with current warp}

end for

Φ =

∑

i=1

{Average warps}

∀iΦ

−1

(Φ

) {Normalise warps by removing

average warp}

r = r/2 {increase resolution}

end while

return Warps {Φ

}

1986). At each edge point found in the source image

a search is made in a small neighbourhood (currently

just the adjacent 9 pixels) in the target image (Figure

2). The most similar point (in terms of ﬁrst or ﬁrst and

second image derivatives) is selected as a potential

match (Algorithm 4). If a potential match is found

the same search is performed for matching edges in

the source image for the target point. If the points

in the source and target images agree the points are

added to the list of matches (Algorithm 3). Once the

search for matches is complete the estimated match-

ing points are used to drive a regularised warp from

the source to the target image. The process is repeated

until the number of matching edges doesn’t increase

(Algorithm 2).

2.2 Warping and Regularisation

Warping is performed using a multi-scale B-spline

based warping function (Lee et al., 1995) that in-

cludes an afﬁne term. We store the non-afﬁne part of

the warping function on a discrete grid. At the lower

scale the non-afﬁne part of the warping function is

regularised. In this work we regularise by ﬁltering

with a B-spline function whose width increases lin-

early with decreasing image resolution. This can be

achieved by repeated ﬁltering with dilated versions of

the same discrete ﬁlter. We ensure that all the par-

tial warps are one-to-one by scaling the warp update

based on the size of the Jacobean at each point in the

warp (Tiddeman et al., 2001). Partial warps are con-

catenated at each iteration, which preserves the one-

to-one property. Each image is warped using the cur-

(a) (b)

Figure 2: (a) For each edge point in the ﬁrst image (top) a

small neighbourhood is searched in the target image (bot-

tom). The most similar edge point (if any) is selected,

and an identical search is made of its neighbourhood in the

ﬁrst image. If the most similar point in this second search

matches the original point the point pair are added to the

warp constraints. (b) Example edges from two images dur-

ing two iteration of our algorithm at different resolutions.

The current estimate of the average is shown in magenta,

the subject in cyan and overlapping pixels in blue.

Algorithm 2: Warp update algorithm.

Require: Images A and B, resolution parameter r

(x,y) = f

∗ A(rx,ry) {Get low resolution ver-

sion}

(x,y) = f

∗ B(rx,ry) {Get low resolution ver-

sion}

old

= 0

new

= 0

Φ = 1 {Initialise warp to identity}

repeat

old

= N

new

(x) = B

(Φ(x)) {Warp image using current

estimate}

({p

},{q

}) = match(A

) {Get matching

edge maxima points, Algorithm 3}

new

= length({p

}) {store the number of

matches found}

φ = interpolate({p

},{q

}) {Interpolate con-

straints}

φ = f

∗ φ {Low pass ﬁlter non-afﬁne part of

warp}

φ = overlap(φ) {Ensure one-to-one property of

partial warp using (Tiddeman et al., 2001)}

Φ = φ · Φ {Compose warp update with current

warp}

until N

new

< N

old

Φ = Upsample( Φ) {Interpolate warp to current

resolution}

return Φ

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

rent estimate of the warp and then the image deriva-

tives are calculated before matching. At the end of

each iteration through the set the warps are upsampled

to match the current resolution. The partial warps are

also normalised by calculating the average warp and

removing the average warp from each partial warp.

We do this for each partial warp by calculating the

average shift and current shift for each point and in-

terpolating between them.

Algorithm 3: Edge matching algorithm.

Require: Images A and B

Calculate {A

} = {A

}

Calculate {B

} = {B

}

Calculate edge maxima E

and E

edgeList = {}

for all pixels x do

if E

(x) then

p = bestMatch({A

},{B

},E

,x) {Algorithm

if p 6=  then

q =bestMatch({B

},{A

},E

, p)

if q = x then

edgeList = append(edgeList, {x, p})

end if

end for

return edgeList

2.3 Application to 3D Surfaces

The method described above for 2D images can be ex-

tended to texture mapped surfaces where the surface

can be parameterised to a 2D rectangle. The facial

surface data we use (3dMD, 2011) is supplied with

a texture map in two halves and the size of the im-

ages and the position of the join line varies with dif-

ferent captures. Also the data contains various holes,

occasionally disconnected regions and sometimes in-

correct texture coordinates. To cope with this kind of

data we ﬂatten the texture map to a single texture im-

age using angle-based ﬂattening (Floater, 2003), al-

though more sophisticated area preserving methods

may improve the results. We only use the largest con-

nected region of the mesh, which usually contains the

face, or extraneous regions can be deleted to ensure

the face region is selected. We also assume approxi-

mate rigid alignment of the 3D models.

In order to produce an average we need to repa-

rameterise all the meshes to have a standard structure.

In this work we just pick one surface to act as the tem-

plate for the mesh (number of vertices, connectivity

etc.). The reparameterisation of the mesh to 2D pro-

duces texture maps that have no relationship to each

other. In order to get the 2D coordinates into approxi-

mate alignment and to initialise the algorithm we use

a non-rigid iterative closest point matching of the 3D

surfaces. Rays are traced from the ”standard” surface

until they intersect the study surface (within a maxi-

mum range). These matches are interpolated using a

multi-level free-form deformation (MFFD), initially

with the minimum grid spacing set to a large size,

to give a smooth warp. The process is repeated with

the grid resolution increasing up to the maximum. At

the ﬁnest scale the texture coordinates at the ray in-

tersection points are used to drive the texture map of

the study surface into approximate alignment with the

standard mesh’s texture map.

Algorithm 4: Point matching algorithm.

Require: Image derivatives {A

},{B

}, edge image

, location x

minerror = ∞, p = 

for all pixels y ∈ Ω

if E

(y) then

error =

∑

i={x,y,xx,yy,xy}

(x) −B

(y))

if error < minerror then

minerror = error

p = y

end if

end for

return p

When all surfaces have been approximately

aligned using the process described above, there are

still residual errors in the alignment of the textures.

We can use the algorithm described above for 2D im-

ages to improve the alignment of the surfaces. Appli-

cation of the algorithm to only the image data could

result in loss of good 3D alignment. In order to avoid

this we also use curvature information from the sur-

face. The surface is mapped to the 2D domain by

sampling the coordinates in the texture space. The

points of maximum concave and convex curvature in

the direction of the associated principal directions are

calculated. The curvature of a surface is independent

of the viewpoint, but is highly dependent on scaling

and regularisation of the surface. We adapt the 2D

algorithm to include the curvature maxima estimated

at the current matching scale. In addition to ﬁnding

matching points of the intensity images, bi-directional

matches are found in the curvature maxima, added to

the list of match points and interpolated. The process

is illustrated in Figure 3.

GROUPWISE NON-RIGID IMAGE ALIGNMENT - Results of a Multiscale Iterative Best Edge Algorithm

Figure 3: The 3D alignment process showing the 3D models and associated texture maps, from left to right: the “standard”

model, an example subject model, the subject after reparameterising using non-rigid ICP and after additional groupwise

alignment. Estimated landmark locations are shown as green dots on the reparameterised 3D models. The non-rigid ICP fails

to position the landmarks correctly (especially around the mouth), whereas the groupwise alignment accurately places the

landmarks.

3 TESTING AND RESULTS

3.1 Average Construction

We have tested the 2D algorithm described above on

a set of 33 front-facing neutral expression male faces

from the IMM database (Nordstrøm et al., 2004),

the ﬁrst 128 frames of the FGNET ”franck” dataset

(FGNET, 2004) and 434 of our own images contain-

ing approximately 13 images of individuals divided

into 4 age groups (child 10-12, teenager 13-19,

young adults 20-49, older adults 50+), 4 approxi-

mate ethnic groupings (white, black, Indian and Chi-

nese) and 2 gender groups. Figure 1 shows the mean

of these sets before and after application of our group-

wise alignment algorithm. Visual inspection of the

averages implies good alignment (on average), but

further tests were conducted to explore the quality of

the models constructed and the alignment speed. We

also tested the 3D algorithm on a set of 75 mixed age

and gender neutral 3D facial surfaces and 110 frames

from a 3D video sequence in the BU-4DFE set (Yin

et al., 2008). The results of blending using only pair-

wise shape alignment and using additional groupwise

alignment are shown in Figure 6.

3.2 Choice of Algorithm

We tested 3 versions of our algorithm using the speci-

ﬁcity measure described in (Cootes et al., 2005):

(a) (b)

Figure 4: Example faces generated from a combined shape-

appearance face model built from the IMM image set using

our algorithm. The models use (a) 5, (b) 10, (c) 15 and (d)

19 components of the combined face model.

1. Performing the alignment in the reference (aver-

age) frame using both 1st and 2nd derivative in-

formation to match edge points,

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

2. Performing the alignment in the target image

frame using ﬁrst and second image derivatives and

3. Performing the alignment in the target frame

using only ﬁrst derivative information (gradient

strength) to match edges.

In order to construct the combined appearance

model we manually delineated the mean image and

used the automatically generated warping functions

to map the points onto individual subjects. The shape

model was built from these points after removing vari-

ations due to rotation, translation and scaling. The

colour model was built from the images aligned using

the dense warping functions. The combined model

was then built using all the shape and colour PCA

weights from all images. The shape weights were

scaled by the square root of the ratio of the sum of

variances to balance their contribution to the model.

All the original images were rigid plus scale aligned

to the mean shape using the estimated points prior to

running the speciﬁcity tests as these parameters are

not constrained by the model.

The model was tested with 15 different numbers

of PCA parameters (from 5 to 19 inclusive). For each

set of parameters 1000 synthetic faces were gener-

ated. Example synthetic faces are shown in Figure

4. For each of these the difference from each original

face (average of absolute pixel differences) was cal-

culated, and the smallest added to the average error.

In previous work each pixel error was minimised over

a small neighbourhood by searching for the nearest

match, but in this work we just use the pixel at the

same location (i.e. the neighbourhood is just a single

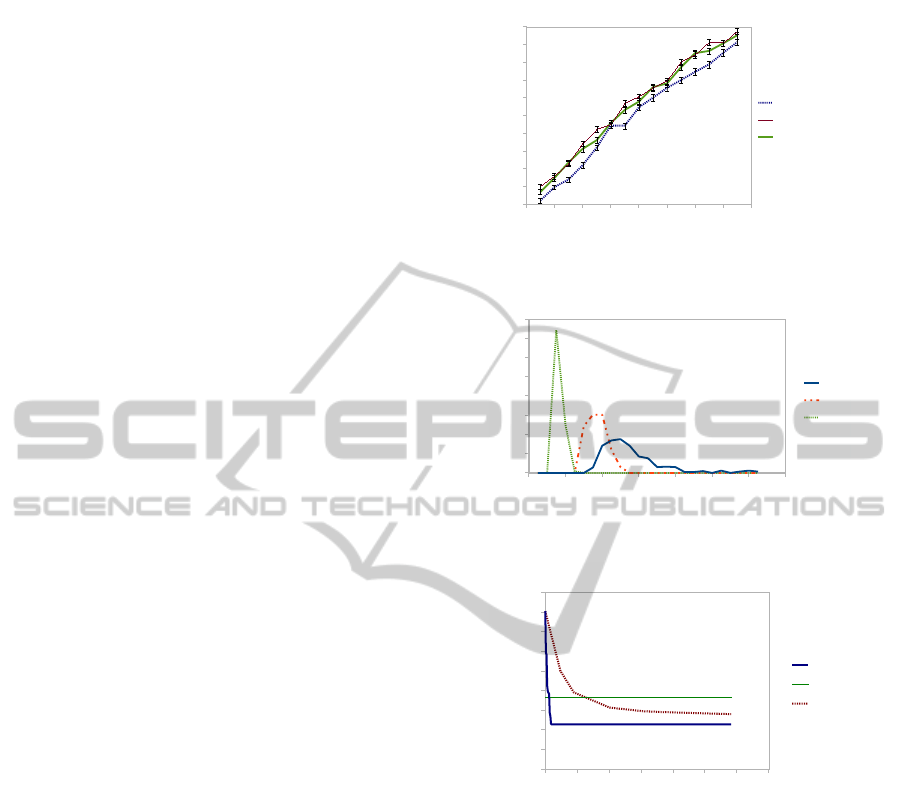
pixel). The results of the speciﬁcity tests are shown

in Figure 5(a). These indicate that (as in previous

work) performing the alignment in the target image

reference frame leads to improved alignment, at the

expense of a small increase in algorithm complexity.

In addition, in this work the inclusion of 2nd deriva-

tive information in the edge matching also leads to an

improvement in the performance.

3.3 Accuracy

In order to compare our algorithm with manual anno-

tations we also used the warping function to project

a delineation of the mean image onto each image in

each set of face images. These automatically gen-

erated points were compared to the manually spec-

iﬁed points by calculating the average distance of

each point from the manually speciﬁed location, di-

vided by the manually speciﬁed eye separation. For

the IMM and FGNET data we used the landmarkings

supplied with these data sets, for our own dataset we

used our own landmark data. The error was calcu-

4 6 8 10 12 14 16 18 20

Specificity comparison

target

reference

1st derivative

PCA Components

(a)

0 2 4 6 8 10 12 14

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Point Error Distribution

sci

imm

fgnet

Error (bin size = 0.5%)

(b)

0 50 100 150 200 250 300 350

0.000

0.005

0.010

0.015

0.020

0.025

0.030

0.035

0.040

0.045

Convergence comparison

IBE

Hand

SPSA

Iteration

(c)

Figure 5: (a) Speciﬁcity comparison demonstrates im-

proved performance for matching in the target image frame

vs reference image frame and for using both 1st and 2nd

derivative information vs only ﬁrst derivative. (b) The dis-

tribution of errors from manually placed landmarks on the 3

image sets shown in ﬁgure 1. (c) Comparison of the conver-

gence speed between the stochastic optimisation algorithm

(SPSA) and our algorithm and hand delineation data on the

ﬁrst 128 frames of the FGNET Franck sequence. (SPSA

and hand data taken from (Sidorov et al., 2009) Figure 6.)

lated as the average point distance as a percentage of

the eye manually speciﬁed eye separation (pupil cen-

tres on FGNET and our data, outer eye corners for

IMM). The results of this experiment are shown in

Figure 5(b) and indicate performance similar to pre-

vious work (e.g. (Cootes et al., 2010)). Unsurpris-

ingly, as the variation within each set increases the

alignment quality decreases.

GROUPWISE NON-RIGID IMAGE ALIGNMENT - Results of a Multiscale Iterative Best Edge Algorithm

(a)

(b)

(c)

(d)

Figure 6: Example output of our 3D algorithm. (a) and (c)

original blends after pairwise alignment with non-rigid ICP

(shape only), (b) and (d) after additional groupwise align-

ment on different images sets. (a-b) 75 3D captures of men,

women and children of varying age and ethnic origin. (c-d)

110 images from one of the BU 3D facial expression se-

quences.

0 2 4 6 8 10 12

0.05

0.1

0.15

0.2

0.25

0.3

0.35

3D Error Histogram

BU-IBE

BU-ICP

Error (bin size = 0.5%)

(a)

0 5 10 15 20 25

0.05

0.1

0.15

0.2

0.25

3D Error Histogram

EF-ICP

EF-IBE

Error (bin size = 0.5%)

(b)

Figure 7: Errors from hand landmarked data for the two

3D datasets shown in Figure 6. Errors are smaller for both

(a) the BU dataset and (b) our own data using the iterative

best edge algorithm (IBE) than using only pairwise iterative

closest point (ICP).

For the 3D surface data a similar experiment was

conducted. Landmarks speciﬁed in 2D on the average

texture map were projected onto each 3D surface us-

ing the estimated warping functions. These automati-

cally generated landmarks were compared with man-

ually speciﬁed 3D landmark locations, and the results

are measured as the average error over the points as a

percentage of the manually speciﬁed eye separation.

In both test sets the IBE algorithm demonstrates su-

perior alignment over pairwise shape only ICP align-

ment on both test data sets (Figure 7).

3.4 Speed

Direct comparison of convergence speed is extremely

difﬁcult, with the risk that differences in the imple-

mentation or tuning effort can dominate the results.

Also, many papers don’t supply precise timings on

standard hardware and image data. With that health

warning in place, we provide results here that are

indicative of performance. We compare the con-

vergence speed (in terms of iteration counts) of our

algorithm to the SPSA based method described in

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

(Sidorov et al., 2009). In the 10 iterations of our

algorithm we achieve a lower error than in approx.

300 iterations of the SPSA algorithm when using the

FGNET franck data (Figure 5(c)). Each iteration of

our algorithm is also fast as it only requires very lo-

cal searches and typically < 5 iterations of the edge

matching (in Algorithm 2) to converge at each scale.

4 CONCLUSIONS

In this paper we have developed a practical groupwise

alignment algorithm that demonstrates efﬁciency and

promising results. The algorithm uses a bottom up ap-

proach, combining many local estimates of the align-

ment using regularisation, rather then searching in a

large parameter space to optimise the alignment met-

ric. This makes the algorithm extremely efﬁcient

and the results seem encouraging, but futher work is

needed to develop a rigorous theoretical underpinning

for the approach and to provide further comparisons

with alternative approaches.

REFERENCES

3dMD (2011). 3dmd stereometric face capture system.

http://www.3dmd.com/.

Canny, J. (1986). A computational approach to edge de-

tection. IEEE Transactions Pattern Analysis and Ma-

chine Intelligence, 8:679–714.

Cootes, T., Twining, C., Petrovi

c, V., Babalola, K., and Tay-

lor, C. (2010). Computing accurate correspondences

across groups of images. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 32(11):1994

– 2005.

Cootes, T., Twining, C., V.Petrovi

c, R.Schestowitz, and

Taylor, C. (2005). Groupwise construction of appear-

ance models using piece-wise afﬁne deformations. In

Proceedings of British Machine Vision Conference

(BMVC), volume 2, pages 879–888.

Cootes, T. F., Edwards, G. J., and Taylor, C. J. (2001). Ac-

tive appearance models. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 23(6):681–

685.

Davies, R., Cootes, T., and Taylor, C. (2001). A minimum

description length approach to statistical shape mod-

elling. Information Processing in Medical Imaging,

2082:50–63.

Davies, R., Twining, C., and Taylor, C. (2008). Group-

wise surface correspondence by optimization: Repre-

sentation and regularization. Medical Image Analysis,

12:787–796.

Di, H., Iqbal, R. N., Xu, G., and Tao, L. (2007). Groupwise

shape registration on raw edge sequence via a spatio-

temporal generative model. In Proc. IEEE Computer

Vision and Pattern Recognition (CVPR), volume 0,

pages 1–8, Los Alamitos, CA, USA. IEEE Computer

Society.

FGNET (2004). Face and gesture network: talking face

database. http://www-prima.inrialpes.fr/FGnet/data/

01-TalkingFace/talking face.html.

Floater, M. (2003). Mean value coordinates. Computer

Aided Geometric Design, 20:19–27.

Hufnagel, H., Pennec, X., Ehrhardt, J., Ayache, N., and

Handels, H. (2008). Generation of a statistical shape

model with probabilistic point correspondences and

em-icp. International Journal for Computer Assisted

Radiology and Surgery (IJCARS), 2(5):265–273.

Lee, S.-Y., Chwa, K.-Y., Shin, S. Y., and Wolberg, G.

(1995). Image metamorphosis using snakes and free-

form deformations. Proc. ACM SIGGRAPH, pages

439–448.

Liu, X., Tong, Y., and Wheeler, F. (2009). Simultaneous

alignment and clustering for an image ensemble. In

Proc. IEEE International Conference on Computer Vi-

sion (ICCV), pages 1327 –1334.

Mallet, S. (1989). A theory for multiresolution signal de-

composition: the wavelet representation. IEEE Trans-

actions on Pattern Analalysis and Machine Intelli-

gence, 11:674693.

Nordstrøm, M. M., Larsen, M., Sierakowski, J., and

Stegmann, M. B. (2004). The imm face database -

an annotated dataset of 240 face images. Technical re-

port, Informatics and Mathematical Modelling, Tech-

nical University of Denmark, DTU.

Rueckert, D., Frangi, A. F., and Schnabel, J. A. (2003).

Automatic construction of 3d statistical deformation

models of the brain using non-rigid registration. IEEE

Transactions on Medical Imaging, 22(8):1014–1025.

Sidorov, K., Marshall, D., and Richmond, S. (2009). An

efﬁcient stochastic approach to groupwise non-rigid

image registration. In IEEE conference on Computer

Vision and Pattern Recognition, pages 2208–2213.

IEEE Computer Society.

Spall, J. (1998). Implementation of the simultaneous pertur-

bation method for efﬁcient optimization. IEEE Trans-

actions on Aerospace Electronic Systems, 34:817–

823.

Tiddeman, B., Duffy, N., and Rabey, G. (2001). A general

method for overlap control in image warping. Com-

puters and Graphics, 25(1):57–66.

Wang, F., Vemuri, B. C., Rangarajan, A., and Eisenschenk,

S. J. (2008). Simultaneous nonrigid registration of

multiple point sets and atlas construction. IEEE

Transactions on Pattern Analalysis and Machine In-

telligence, 30(11):2011–2022.

Wang, Q., Wu, G., Yap, P.-T., and Shen, D. (2010). At-

tribute vector guided groupwise registration. Neu-

roImage, 50:1485–1496.

Yin, L., Chen, X., Sun, Y., Worm, T., and Reale, M.

(2008). A high-resolution 3d dynamic facial expres-

sion database. In The 8th International Conference on

Automatic Face and Gesture Recognition (FGR08).

ollei, L., Learned-Miller, E., Grimson, E., and Wells, W.

(2005). Efﬁcient population registration of 3d data.

Computer Vision for Biomedical Image Applications,

3765:291–301.

GROUPWISE NON-RIGID IMAGE ALIGNMENT - Results of a Multiscale Iterative Best Edge Algorithm