REGION-BASED OBJECTIVE EVALUATION
OF POLYGONAL MESH SEGMENTATION METHODS
Amira Zguira, Narjes Doggaz and Ezzeddine Zagrouba
University La Manouba, Laboratory RIADI
Team of Research on Intelligent Imaging and Computational Visio, Manouba, Tunisia
Keywords: 3D mesh, Region type, Segmentation, Evaluation, Ground-truth.
Abstract: In this paper, we propose a new region-based objective evaluation approach of polygonal mesh
segmentation algorithms. This approach is derived from 2D-images segmentation similarity measures. We
quantify an evaluation criterion relatively to each type of segmented mesh-regions, based on a mesh
classification method into convex, concave and planar regions. We apply this approach on eight well-
selected existing algorithms conducted by a heterogeneous ground-truth. We present and discuss the
evaluation results of these techniques by taking into account the corresponding objects’ classes in every type
of region. This provides better understanding as to the strengths and weaknesses of each technique in
function of each mesh-regions type. That aims to make a better choice concerning the segmentation
algorithms for different applications.
1 INTRODUCTION
The evaluation of segmentation methods is an area
of recent research for 3D polygonal meshes
segmentation. Until now, few researchers have
addressed this problem. Recent works (Benhabiles et
al., 2009; Chen et al., 2009) proposed ground-truths
and quantitative 3D measures for an objective
evaluation drawing from 2D evaluation measures.
However, these measures evaluate only the obtained
results quality for the whole given image and they
cannot be adapted to assess the consistency of a
segmentation method in relation to each type of
segmented mesh region.
Adjudging objectively and quantitatively the
quality of segmentation for each type of segmented
region is the main inspiration of this paper. We
propose three quality measures that quantify the
similarity of each type of region of the ground-truth
relatively to the segmentation obtained by an
automatic algorithm. Section 2 synthesizes related
works. We present our evaluation approach in
section 3. In section 4, we describe the process of
segmented regions classification. Section 5 details
the three objective metrics for each type of region.
In section 6, we apply our three measures on eight
well-selected existing algorithms and then we
analyze their evaluation results. Finally, we
conclude.
2 RELATED WORK
Attene et al. (Attene et al., 2006a) emphasized the
difficulty of evaluating the segmentation quality
given the different contexts of use. They conducted a
comparative study of segmentation algorithms in
which they have proposed several evaluation
criteria, namely type of segmentation, complexity,
sensitivity to pose, etc. These criteria are very
important, but they are not sufficient to quantify the
evaluation of the segmentation towards the human
visual perception. Recently, Benhabiles et al.
(Benhabiles et al., 2009) have proposed an objective
evaluation approach of 3D mesh segmentation
algorithms which is based on two measures of
consistency error (local and global). They tested the
proposed measures on two recent 3D mesh
segmentation algorithms. These measures are based
on a ground truth corpus containing some various
3D objects models with their manual segmentations
produced by human observers. However, this corpus
contains a limited set of 3D models that are
manually segmented. In the same context, Chen et
al. (Chen et al., 2009) have proposed a benchmark
which contains a comparative study of seven 3D
mesh segmentation algorithms. They tested these
algorithms on a large base of 3D mesh models. They
introduced four quantitative evaluation criteria.
205
Zguira A., Doggaz N. and Zagrouba E..
REGION-BASED OBJECTIVE EVALUATION OF POLYGONAL MESH SEGMENTATION METHODS.
DOI: 10.5220/0003327702050209
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 205-209
ISBN: 978-989-8425-47-8
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

However, their proposed criteria reflect an overall
evaluation of the mesh segmentation. In fact, these
criteria evaluate only the quality of the obtained
results for a given image without taking into account
the evaluation against each type of segmented
region.
Our work offers an analysis of the quality of
segmentation in relation to each type of segmented
regions (convex, concave or planar). This evaluation
provides a better understanding of the use of certain
criteria during the mesh segmentation process. It
also measures the performance of a segmentation
method relatively to the type of segmented 3D
object regions.
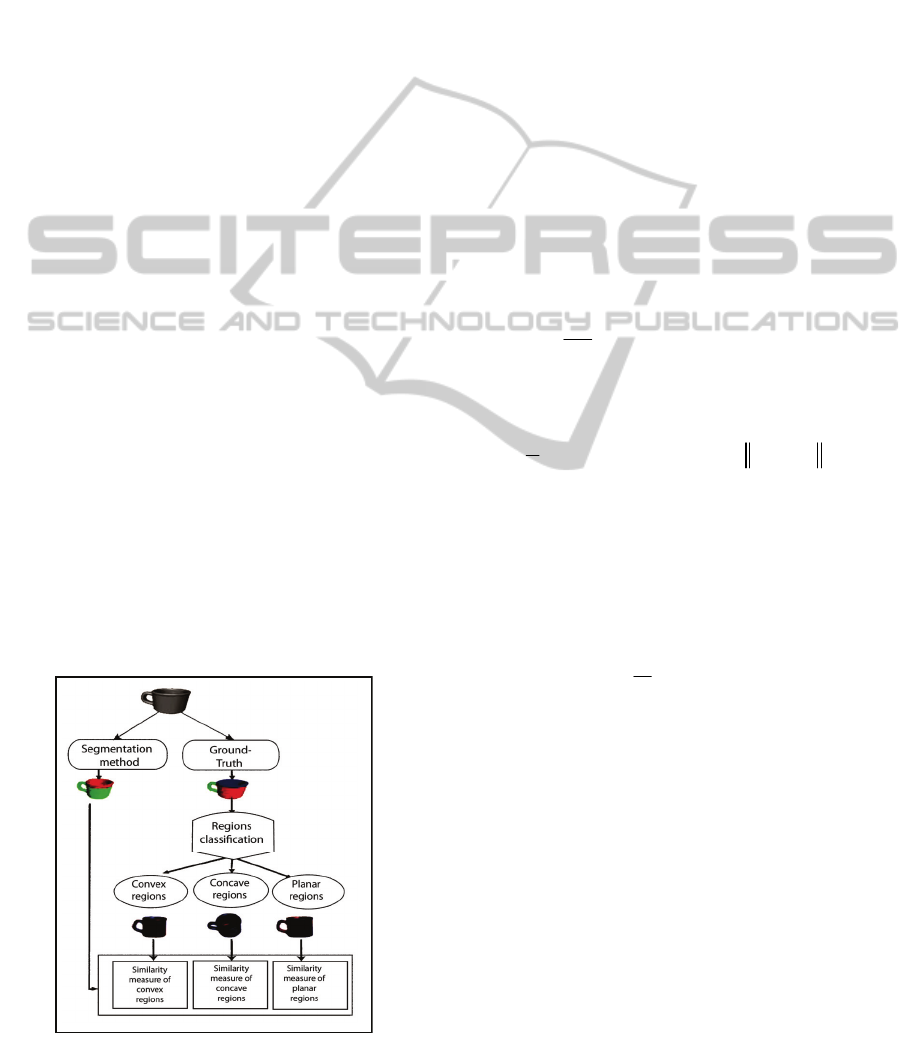
3 FRAMEWORK
OF OUR APPROACH
Our approach is inspired from 2D-images
segmentation evaluation method (Amri and
Zagrouba, 2006). In fact, Amri and Zagrouba (Amri
and Zagrouba, 2006) have defined two measures for
the evaluation of regions segmentation algorithms
which we have generalized for 3D-mesh
segmentation evaluation.
First of all, having the ground truth of an image,
our approach begins by classifying the regions
constituting the ground truth into three classes:
convex, concave and planar. This classification is
based on the computation of the principal curvatures
of each segmented mesh region. Then, the automatic
segmentation quality is objectively evaluated
relatively to the different region types. To do this,
three similarity measures are proposed which each
measure is relative to a region type (Figure1).
Figure 1: Framework of our approach.
4 CLASSIFICATION PROCESS
The aspect of convex, concave or planar regions
prove to be an important criterion to separate the
majority of the caracterisitc features of meshes.
Thus, we started our approach by a classification
process which allows identifying automatically the
type of each region of the 3D-image reference
(convex, concave or palnar). Indeed, they exist in the
literature several methods to classify the different
regions of a 3D mesh; these methods are based on
different topological and geometrical properties of
the mesh. We opted for the classification of regions
according to the values of mean and Gaussian
curvatures due to its accuracy, consistency and
simplicity of its implementation. For this goal, we
have applied the work of Meyer et al. (Meyer et al.,
2002), using averaging Voronoi cell and the mixed
Finite-Element/Finite-Volume method. We have
calculated the mean curvature (1) and the Gaussian
curvature (3) following the below equations.
1
()
1
() (cot cot )( )
2
m i ij ij i j
jN i
Cx x x
A
αβ
∈
=+−

(1)
Where A is the Voronoi area region in the vertex
i
x
:
1
2
()
1
(cot cot )
8
ij ij i j
jN i
A
xx αβ
∈
=+−

(2)
Where
ij
α
and
ij
β
are the angles of the side
(
i
x
,
j
x
) and
1
()Niis the 1-ring neighbours around
vertex
i
x
. Calculating the Gaussian curvature is
remanded to use equation (3):
1
1
() (2 )
f
g
ij
j
Cx
A
πθ
=
=−

(3)
Where f is the number of adjacent faces to the
vertex
i
x
and
j
θ is the angle of the face j in
i
x
.
After estimating the curvatures values for region
vertices, we deduced the curvature values for the
whole region of a segmented object. We repeat this
curvature calculation, in the same way, for all
regions of the same mesh and then for all ground-
truth segmented models. The mean and Gaussian
curvature values can be positive, negative or null.
Finally, according to the curvature estimation done
in the previous step, we can deduce which region is
convex and which is concave from which that is
planar. The first class presents the convex regions
with positive both mean curvature and Gaussian
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
206

curvature. The second is concave regions with
positive Gaussian curvature and negative mean
curvature. The last class is the class of planar
regions having almost null or negative Gaussian
curvature.
5 SIMILARITY METRICS
The next step of our approach is to develop a metric
of an objective quantitative evaluation relatively to
each region type.
Given a set of n images,
{
}
/1
k
I
Ikn=≤≤,
we associated relatively to each image
k
I
a set of
automatic segmented regions
k
Seg
= {
1
k
R
…
k
N
k
R
},
and a set of manual segmented regions
k
R
ef
=
{
1
k
r …
k
M
k
r }. Where N is the number of regions of
the automatically segmented mesh and
M
is the
number of regions of the manually segmented mesh.
After the classification step, we obtained three
regions classes
cnv
k
R
ef
={
j
k
r /
j
k
r convex},
ncc
k
Ref
={
j
k
r /
j
k
r concave}and
ln
p
k
Ref
={
j
k
r /
j
k
r planar},
where
k
R
ef
=
cnv
k
R
ef

ncc
k
R
ef

lnp
k
R
ef
.
For each image
k
I
, a similarity table
k
T is
calculated (4), where each element
(, )
k
Tij is
defined as:
()()
1
(, )
2() ()
ij ij
kk kk
k
ij
kk
card R r card R r
Tij
card R card r

=+



(4)
We define then three similarity measures associated
respectively to convex, concave and planar regions
(5). Each of these measures evaluates the faculty of
an algorithm to segment each type of zones
(
,,type convex concave planar= ).
1
1
1/
1
max( ( , )
k
jtype
k
kk
M
n
k
iN
k
jrRef
n
typ e
n
typ e
k
k
Tij
Z
M
≤≤
=
=∈
=




=


(5)
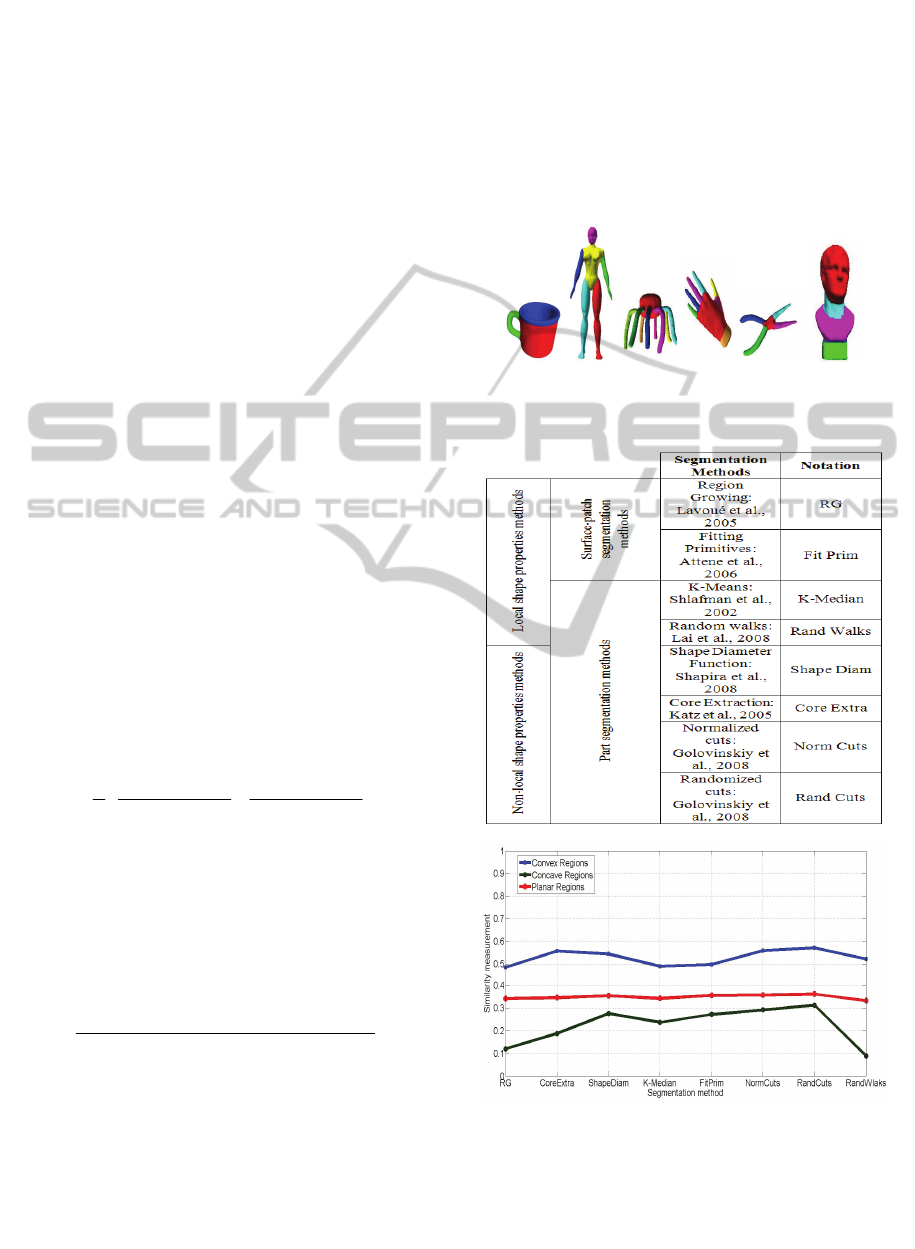
6 EXPERIMENTS
To validate our evaluation approach, we have firstly
selected a corpus of 3D mesh models. Indeed, our
data set contains globally 42 models, regrouped in
six classes (varied objects, Human, Animals, Hand,
CAD and Bust), containing each one seven models.
We selected this set of meshes and its corresponding
ground-truth (figure2) from the benchmark (Chen et
al., 2009). We have selected secondly eight 3D mesh
segmentation methods (Table1). To make our
choice, we have mainly focused on recent works.
Moreover, we favoured approaches that adopt a
semantic segmentation (part segmentation methods).
Figure 2: Some ground-truth segmented models.
Table 1: The selected regions segmentation methods.
Figure 3: Segmentation evaluation according to the three
similarity measurements.
Figure 3 illustrates the three proposed similarity
measures (eq. 5). For a given segmented method, a
high value of a similarity measure of convex regions
REGION-BASED OBJECTIVE EVALUATION OF POLYGONAL MESH SEGMENTATION METHODS
207

(respectively concave and planar) indicates a good
fit of the method in question for the segmentation of
convex regions (respectively concave and planar).
Our experimental results have shown that the
segmentation techniques adopting non-local shape
properties (Rand Cuts, Norm Cuts, Core Extra and
Shape Diameter) are better than those based on the
local shape properties. We note in particular that
Rand Cuts is the best method to segment convex,
concave and planar regions. Nevertheless,
segmentation by Rand Walks is the least suited for
the segmentation of planar and concave regions. The
RG method is however the less good for segmenting
convex regions.
The results concerning the evaluation of the
convex and concave regions segmentation present
the quality measures the most dispersed
(variance
cnv
= 0.00119277, variance
cnc
= 0.0087033).
This is explained by the variety of the convex and
the concave forms, which can be segmented in
different ways by methods using various criteria.
However, planar regions segmentation methods
evaluation present the similarity measures the most
closest (variance
pln
= 9.6161E-05). Indeed, the planar
regions have the same geometric shape to be
segmented in nearly the same way and it helps to
have very similar results.
Moreover, our results concerning planar regions
show the performance of some algorithms that are
frequently used in CAD (Computer Aided Design)
in the segmentation of such regions. For example,
the method Fit Prim, which is composed of
geometric primitives, such as CAD models, is the
best suited for the segmentation of this type of object
(Attene et al., 2006b).
Thus, the criteria used in each method in the
segmentation process have an influence on the
quality of segmented regions. Indeed, each method
uses some criteria to guide the segmentation process
where the type of extracted regions depends on the
adopted criteria. Therefore, through the
classification phase done before the application of
the evaluation metric, our approach provides better
understanding of the use of these criteria in the mesh
segmentation process. This allows providing a better
comparison of the strengths and the weaknesses of
each technique in the segmentation of each type of
the mesh regions. For that reason, we thought to
evaluate the performance of a segmentation method
on each regions type of the image and not on the
entire image. Furthermore, this approach may help
in making the better choice of the segmentation
algorithm that is the most adapted to each 3D image
zone and this can be in applications such as:
watermarking, compression, medical imaging, etc.
7 CONCLUSIONS
This paper proposes a new approach of objective
quantitative evaluation of 3D mesh segmentation.
For this purpose, we have firstly selected a corpus of
various 3D models and their ground-truth. We have
adopted secondly a method for the classification of
segmented regions of each ground-truth object
according to the values of its principal curvatures.
Then, we have proposed three similarity measures
for the evaluation of the segmentation quality for
every region type (convex, concave or planar). To
validate our approach, we have selected eight recent
segmentation algorithms on heterogeneous images.
In terms of improving our results, there are a
number of interesting directions to explore.
Currently, we are working to fusion the compared
methods permitting to combine the results of the best
selected algorithms for each type of region. We also
plan to perform experiments with larger corpus in
terms of number of images to establish a complete
comprehensive study for an objective evaluation of
the 3D meshes segmentation.
REFERENCES
Amri S. and Zagrouba E. (2006). Evaluation and fusion of
image segmentation methods. In ICTTA :
International Conference on Information &
Communication Technologies: From Theory to
Applications, vol. 1, 1524-1529.
Attene M., Katz S., Mortara M., Patan G., Spagnuolo M.
and Tal A. (2006). Mesh segmentation, a comparative
study. In SMI : Proceedings of the IEEE International
Conference on Shape Modeling and Applications
2006, IEEE Computer Society, Washington, DC,
USA, 7.
Attene, M., Falcidieno, B., and Spagnuolo, M. (2006).
Hierarchical mesh segmentation based on fitting
primitives. Vis. Comput., vol. 22(3), 181-193.
Benhabiles H., Vandeborre J., Lavoué G. and Daoudi M.
(2009). A framework for the objective evaluation of
segmentation algorithms using a ground-truth of
human segmented 3d models. In SMI : Proceedings of
the IEEE International Conference on Shape
Modeling and Applications, 36-43.
Chen X., Golovinskiy A. and Funkhouser T. (2009). A
Benchmark for 3D Mesh Segmentation. ACM
Transactions on Graphics (Proc. SIGGRAPH), vol.
28(3), 1.
Golovinskiy A. and Funkhouser T. (2008). Randomized
cuts for 3D mesh analysis. ACM Transactions on
Graphics (Proc. SIGGRAPH ASIA), vol. 27(5), 145-
157.
Katz S., Leifman G. and Tal A. (2005). Mesh
segmentation using feature point and core extraction.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
208

Vis. Comput., vol. 21(8), 649-658.
Lai Y.-K., Hu S.-M., Martin R. R. and Rosin P. L. (2008).
Fast mesh segmentation using random walks. In ACM
Symposium on Solid and Physical Modeling. 183-191.
Lavoué G., Dupont F. and Baskurt A. (2005). A new cad
mesh segmentation method, based on curvature tensor
analysis. Computer-Aided Design, vol. 37(10), 975-
987.
Meyer M., Desbrun M., Schröder P., and al. (2002).
Discrete Differential-Geometry Operators for
Triangulated 2-Manifolds. International Workshop on
Visualization and Mathematics, Berlin, Germany, 35-
57.
Shapira L., Shamir A. and Cohen-Or D. (2008). Consistent
mesh partitioning and skeletonisation using the shape
diameter function. Vis. Comput., vol. 24(4), 249–259.
Shlafman S., Tal A. and Katz S. (2002). Metamorphosis of
polyhedral surfaces using decomposition. Computer
Graphics forum, vol. 21(3), 219-228.
REGION-BASED OBJECTIVE EVALUATION OF POLYGONAL MESH SEGMENTATION METHODS
209