
LEARNING OBJECT DETECTION USING
MULTIPLE NEURAL NETWORKS
Ignazio Gallo and Angelo Nodari
University of Insubria, Dipartimento di Informatica e Comunicazione, Varese, Italy
Keywords:
Object detection, Neural networks, Multiple neural networks.
Abstract:
Multiple neural network systems have become popular techniques for tackling complex tasks, often giving
improved performance compared to a single network. In this study we propose an innovative detection al-
gorithm in image analysis using a multiple neural network approach where many neural networks are jointly
used to solve the object detection problem. We use a group of networks configured with different parameters
and features, then combines them in order to obtain new networks. The topology of the set of neural networks
is statically configured as a tree where the root node produces in output the detection map. This work repre-
sents a preliminary study through which we want to move from detection to segmentation and recognition of
objects of interest. We have compared our model with other detection algorithms using a standard dataset and
the results are encouraging. The results highlight the advantages and problems that will guide the evolution of
the proposed model.
1 INTRODUCTION
Object detection is an important task in computer vi-
sion, it is a critical part in many applications such
as content based image retrieval, understanding of a
scene, automatic annotations, etc. However it is still
an open problem due to the heterogeneity of some
classes of objects to be detect and the complexity of
the background in some images. Many works avail-
able in literature work well only on certain categories
of images and fall on others. In this paper we propose
a method capable of maintaining the same accuracy
on different types of data.
Usually the object of interest in a digital image is
detected finding the bounding box which surround the
object. The strength of this work consist in the detec-
tion of the object in a cognitive manner, locating the
object through the use of a segmentation process. De-
tection and segmentation of an object in a single step
is certainly a more complex and difficult operation in-
stead of detect an object and perform a segmentation
in a second step. In this work we use only the detec-
tion phase of our algorithm in order to compare the
results with other object detection techniques despite
the algorithm presented performs also a segmentation
of the object of interest.
In literature there are many object detection ap-
proaches which can be classified as bag of words
model (Csurka et al., 2004; Fei-fei, 2005; Schmid,
2006), parts and structure models (Fischler and
Elschlager, 1973; Fergus et al., 2003; Crandall et al.,
2005), discriminative methods (Bouchard and Triggs,
2005; Zhu and Yuille, 2006) and combined segmen-
tation and recognition methods (Leibe and Schiele,
2003; Todorovic and Ahuja, 2006). In this work,
choosing to work with neural networks that combine
the segmentation and recognition, we can classify our
algorithm in the latter object recognition approach.
The model proposed in this study, like other works
which propose biologically inspired systems (Riesen-
huber and Poggio, 1999; Serre et al., 2005), is in-
spired by the human visual perception system. In
fact, analyzing how the visual system works, a neu-
ron n of the visual cortex receives a bottom-up sig-
nal X from the retina (lower-level-input) and a signal
M from an object-model-concept m (top-down prim-
ing signal). The neuron n is activated if both signals
are strong enough. The visual perception uses many
levels in the transition from the retina to object per-
ception. By analogy, we propose a Multi-net system
(Sharkey, 1999) based on a tree-structure where leaf
nodes represent the bottom-up signal extracted from
the input image. The intermediate levels nodes repre-
sent the knowledge of the previous experience, going
in the direction of the root node.
In this paper, unlike for Perceptron Decision
131
Gallo I. and Nodari A..
LEARNING OBJECT DETECTION USING MULTIPLE NEURAL NETWORKS.
DOI: 10.5220/0003328301310136
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 131-136
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Tree (Utgoff, 1988) which has a similar structure to
the method presented here, the prediction of a trained
network can become an input feature of a second neu-
ral model. Starting from the root node of a tree of
neural networks, the training process is propagated to
the leaf nodes of the tree (networks that depend only
by simple features). During the detection phase, each
node gives its generated map to its parent node un-
til the map produced by the root node. Each node
reads its information through a sliding window that
receives all the input features. Neural networks are
trained on the same set of training images and the
prediction of each of them is combined in order to
improve their generalization attitude. The peculiarity
of the proposed model is that each level of the tree is
guided by the same rules: for each node the percep-
tion of small and particular features or the knowledge
of more abstract and complex concepts is performed
by the same mechanism described above, but using a
different node configuration.
2 THE PROPOSED METHOD
In this section we present our model called Multi-Net
for Object Detection (MNOD). The MNOD model
consists of a tree of single networks C
n
P
(F), where n
is the node identifier, P corresponds to all the param-
eters from which the network configuration depends
and F represents the set of input features.
Each neural network C
n
uses a particular set of
parameters P such as training epochs, number of neu-
rons in the input layer, number of neurons in the hid-
den layer, etc.. The set of features F can be directly
extracted from the input images (such as edges, color,
etc...) or they can be the result of other neural models
C
n
P
previously trained on the same training set. Fig-
ure 1 shows an example of a generic MNOD.
Each node C
n
P
produces in output a map where the
pixels containing higher values identify the objects of
interest. As said in (Sharkey, 1999) it is possible to
diversify a node C
n
P
changing network initialization
conditions, topologies, training algorithms and train-
ing data. Here, we investigate only in changing the
network topology considering the set of parameters
P. The main parameters associated which each node n
are P
n
= {I
S
,W
S
}, where I
S
represents the re-sized im-
age dimension and W
S
is the sliding window dimen-
sion. The structure of a single node used in this work,
is showed in Figure 2. It consist in a Multi-Layer Per-
ceptron (MLP) which receives the input values from a
sliding window for each feature configured. We cre-
ate an image for each feature and all these images
are re-sized to the pre-definite dimension. By using
different combinations of these two parameters it is
possible to construct models specialized in the recog-
nition of a specific element of interest in a particular
scale. This concept is typical of Multi-net systems
which use a “modular combination” of the neural net-
works (Sharkey, 1999). In this case the main prob-
lem is divided into sub-tasks and then it is possible to
obtain a solution by combining different modules, or
neural networks.
During the training phase all the input and output
images of a node n are re-sized to the same size I
S
∈
P
n
and from all the gray values in the sliding window
we construct the input and desired output (as showed
in Figure 2).
A single node in the proposed model can be
trained or used directly in generalization unless it re-
ceives in input the output of another neural model (see
for example the nodes C
1
P
1
e C
3
P
3
in the Figure 1).
Otherwise (see, for example nodes C
2
P
2
e C
4
P
4
in the
Figure 1) we first need to train and then to use the
networks of child nodes. For more details on the al-
gorithms used for training the model see the Algo-
rithm 1 and the Figure 2, while for generalization see
Algorithm 2 and Figure 2.
Algorithm 1: Creating the training set for a node C
n
P
(F).
Require: Let D = {(I
in
1
,I
out
1
),...,(I
in
T
,I
out
T
)} the set
of images pairs;
1: for all (I
in
t
,I
out
t
) ∈ D do
2: create images F
1
,...,F
N
from I
in
1
3: if ∃F
i
which is the output of a child node C
m
then
4: execute this algorithm for the node C
m
5: train the node C
m
6: use the trained model to create the image F
i
7: end if
8: Resize F
1
,...,F
N
and I
out
t
at dimension I
S
∈ P
9: Create an input and an output pattern for each
position of the sliding window W
S
∈ P (step s
depends by the image size I
S
)
10: end for
Figure 1: Generic structure of the proposed MNOD model.
The nodes C
n
P
represent the supervised neural models which
receive their input directly from the input features, the nodes
F
i
are the feature maps extracted from the input images.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
132

Figure 2: Generic structure of a node C
n
P
(F
1
,... ,F
N
). The
features F
1
,... ,F
N
are created from each input images I
in
t
.
All the features images are re-sized in according to the pa-
rameter I
S
∈ P in
¯
F
1
,... ,
¯
F
N
. The output image I
out
t
is hand-
segmented and contains higher values for the pixels belong-
ing to the objects of interest. The input patterns of the neural
model are generated using a sliding window of size W
S
∈ P
which reads from the re sized images
¯
F
1
,... ,
¯
F
N
, while the
desired output is derived from the re sized output image
¯
I
out
t
.
Algorithm 2: Generalization of a single node C
n
P
(F).
Require: an image I
in
to pass in input to the trained
model
1: create F = {F
1
,...,F
N
} from I
in
for the node C
n
2: if ∃F
i
which is the output of a child node C
m
then
3: apply this algorithm to the node C
m
4: end if
5: Resize F
1
,...,F
N
at dimension I
S
∈ P
6: Create an input pattern for each position of the
sliding window W
S
∈ P (step 1)
7: Store output predictions of node C
n
P
(F)
8: Compose the output image using the average ac-
tivation values for each pixel
3 EXPERIMENTS
In this study, two types of experiments were con-
ducted to analyze different aspects of the proposed
model. We first analyzed the main parameters of the
MNOD models and its generalization attitude. Fi-
nally, we tried to compare our model with the results
obtained by other methods using a standard dataset.
The two variables of interest to measure the ac-
curacy of an object detection system, are the num-
ber of correct detections that we want to maximize,
and the number of false detections that we want to
minimize. When an object detection system is really
used, we are interested to know how many objects
have been identified, and how often the items found
are false. This compromise can be captured by study-
ing the Precision-Recall curve (or PR-curves), where
P =
correct
actual
, R =
correct
possible
(1)
stating that correct is the number of objects correctly
detected by the system, actual is the total number of
objects recognized by the system, possible is the total
number of objects we expected from system. A Pre-
cision equals to 1.0 means that each detected object is
correct, but tells us nothing about the objects that have
not been found. A high Precision value ensures that
there are few false positives. A Recall measure equals
to 1.0 tells us that each object was correctly identi-
fied, but tells us nothing about how many other items
were incorrectly matched. A measure that usually is
used to summarize Precision and Recall values is the
F-measure F1 = 1/(λP + (1 − λ)R) setting λ = 0.5.
Average Precision (AP) is another measure that ap-
proximates the area under the PR-curve and that, for
its readability, is usually used to compare different ob-
ject detection algorithms. For more details on these
measures and how an object is considered correctly
detected see (Everingham et al., 2005).
3.1 Analysis of Key Parameters
In this experiment we analyzed the behavior of the
MNOD model varying its key parameters. In partic-
ular, we analyzed the influence of the image size I
S
and the sliding window size W
S
parameters, applied
to nodes (or networks) configured with different fea-
tures.
The dataset used here contains real images of cars
viewed from different viewpoint: side, rear, top, front,
partial (see some examples in Figure 4). In particular,
we used the dataset called TU-Graz cars contained in
VOC2005 (Everingham et al., 2005).
For this experiment we used a limited set of fea-
tures that highlight some information on color and
high frequencies available in the images. In partic-
ular, we used the features Saturation (Sa), Hue (Hu),
Sobel (So) and Horizontal Edges (EH).
The MNOD topology is shown in figure 3 and
was fixed before starting the training phase. Nodes
were configured randomly by tying the window size
W
S
< I
S
and trying some combinations of parame-
ters (W
S
,I
S
) leading to an increase in detection ac-
curacy. The size of the sliding window ranges from
1 × 1 to 9 × 9, while the images were scaled propor-
tionally so that the smaller side is in the range [3,24].
LEARNING OBJECT DETECTION USING MULTIPLE NEURAL NETWORKS
133

The plots in Figure 5 show the behavior of the F-
measure in the space (W
S
,I
S
). It is evident that the
range [F1
min
,F1
max
] and the activation area of the F1
measure increases, moving from leaf nodes towards
the root node C
5
.
Based on the results obtained with this first anal-
ysis we chosen a configuration for each node of the
model shown in Figure 3. Each node C
n
was trained
with the following parameters: C
3
20,6
(Sa,Hu, So),
C
1
20,8
(Hu), C
2
23,2
(EH,C
1
), C
4
18,7
(C
3
,C
2
,EH) and
C
5
23,8
(Hu,C
4
).
From Table 1, we may observe that each node of
the selected configuration, if it receives in input the
output of one or more nodes, increases the generaliza-
tion capability. In fact, the Table 1 shows an increase
in P, R and F1, comparing a node with its child nodes.
For example, the last row of the table shows the net-
work C
5
23,8
(Hue,C
4
) that takes advantage of the map
generated by the network C
4
.
Table 1: Results obtained using some different random con-
figurations. C
x,y
(M
1
,M
2
,... ) is a neural network that uses
an image size x × x, a sliding window size y×y, reading the
input values from all the feature M
i
.
Configuration P R F1
C
3
20,6
(Sa,Hu, So) 0,11 0,11 0,11
C
1
20,8
(Hu) 0,02 0,02 0,02
C
2
23,2
(EH,C
1
) 0,05 0,10 0,07
C
4
18,7
(C
3
,C
2
,EH) 0,24 0,19 0,21
C
5
23,8
(Hu,C
4
) 0,33 0,26 0,29
Figure 3: A configuration example where each node in-
creases the accuracy measures (see Table 1 for details) using
the output of child nodes.
All the nodes in Table 1 were trained using 108
training images while results shown in same table are
taken from the test set consisting of 128 never seen
images. The train and test sets are the same of the
VOC2005 dataset 1. Each network was trained using
the learning algorithm Rprop (Resilient Backpropaga-
tion) proposed by Riedmiller and Braun (Riedmiller
and Braun, 1993).
Figure 4: Some examples of images belonging to the dataset
TU-Graz cars.
Figure 5: Each image shows how the F-measure varies in
the parameter space (I
S
,W
S
) for each node C
1
I
S
,W
S
- C
5
I
S
,W
S
shown in Figure 3. A white pixel represents a F-measure
equals to the maximum value. Each network was trained on
10 images of the training set and the F-measure was com-
puted on the first 10 images of the testing set TU-Graz cars.
3.2 Comparisons
In (Everingham et al., 2005) several innovative meth-
ods for object detection were evaluated on a dataset
containing four classes of objects: motorbikes, bi-
cycles, people and cars. The training and test sets
contain objects having substantial variations in terms
of scale, occlusion, and variability within the class.
These aspect of the dataset allow to better assess an
algorithm and to highlight the benefits and drawbacks
of the same algorithm. Another advantage of this
dataset is the possibility to compare an algorithm with
the whole community that used it.
Our algorithm requires the presence of a GT-Mask
for each training image, and not all the four classes
of objects have that information associated with each
training image. For this reason we used only three
classes of objects bicycles, people and cars and for
each class we use only the training image having a
GT-Mask.
The metrics used here are the same as that used
in (Everingham et al., 2005): the PR-curve and the
Average Precision (AP).
The network showed in Figure 6 represents the
structure used in all the three classes of objects. The
structure of the model used in this experiment was
built with the following rule: we build some of the
nodes which receive in input some features and are
configured with a small I
S
value, the maps generated
by these nodes are passed in input to other nodes that
increase the I
S
value, and so on. In this way we can
see a refinement of the segmentation result through
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
134
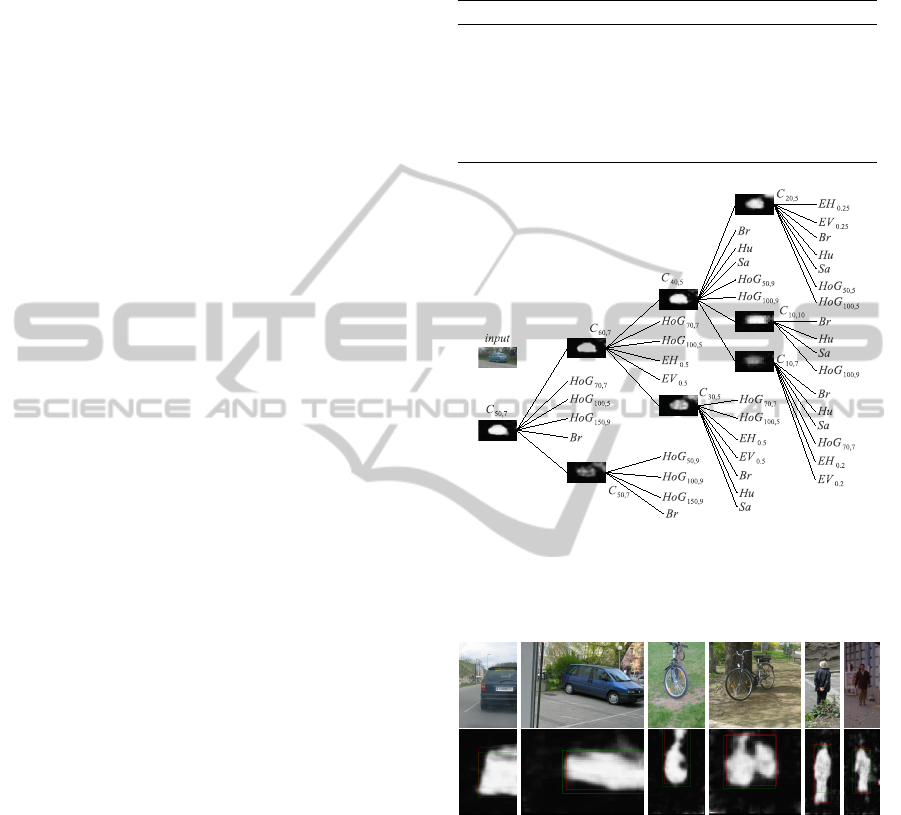
every level of the tree towards the root node.
From this experiment we found that the main
problem of our algorithm lies in the dataset with large
differences of scale. Then, trying to force in input
only the area containing the object (see some exam-
ples showed in the first row of the Figure 7), we note
that the results increase significantly (see MNOD-SI
in Table 2). The model so trained and tested was re-
named MNOD-SI.
In this work a detailed analysis on the best features
for this model has not been done. For this experiment
we used a limited set of features that highlight some
information on color and high frequencies present in
the images. In particular, we used the features Sat-
uration (Sa), Hue (Hu), Brightness (Br), Horizontal
Edges (EH), Vertical Edges (EV ) and Histogram of
Gradient (HoG) configured in different ways. The
parameter s in EH
s
and EV
s
is the scale used on the
input image before to compute the feature. The pa-
rameters (s,b) in HoG
s,b
are the scale used on the in-
put image and the block size respectively. The HoG
feature, as in (Dalal and Triggs, 2005), reads the in-
put values from a sliding window of histograms (cell
block). In this work each histogram is composed by
four bins, a cell block is an area of 6 × 6 pixels and
the neural model used, instead of the SVM, is a MLP.
In Table 2 we compare our model with some meth-
ods presented in (Everingham et al., 2005), while in
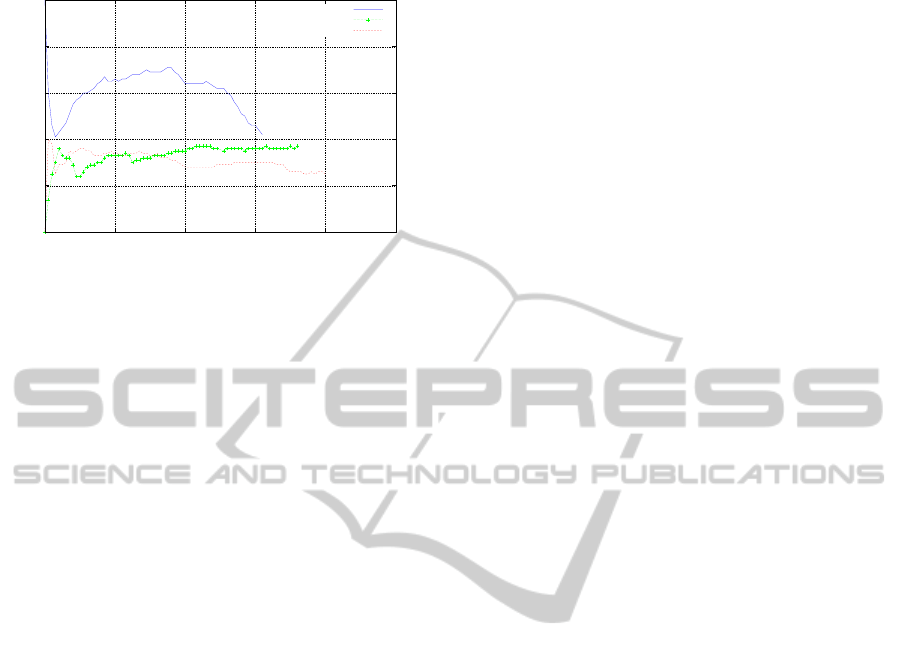
Figure 8 the trend of the PR-curve using MNOD-SI
is shown for the three classes of objects. The AP
measure on the three classes of problems considered
was computed using the same configuration showed
in Figure 6 and the standard test set called test1 for
each class of objects of the VOC 2005 Dataset 1.
It is obvious that we could obtain better results by
making a thorough search of the parameters and of the
features, as evidenced in the study showed in Figure 5,
but we will deal with this issue in a future work. Start-
ing from the results obtained using the model MNOD-
SI we are working for a new version able to exploiting
the different scales in images of a particular domain.
A very interesting result is the fact that the model has
a similar behavior on different classes of objects.
4 CONCLUSIONS
In this paper we described an object detection algo-
rithm based on a multiple networks system. It is
composed by a set of neural networks aggregated to-
gether to provide a single output result. The model
was tested and the results were presented, highlight-
ing the potentialities of our solution. The proposed
algorithm can be configured for different classes of
Table 2: Average precision for the object detection problem
applied to the test set called test1 in VOC 2005 Dataset 1.
The comparison results are taken from (Everingham et al.,
2005).
Method Bicycles People Cars
MNOD 0.01 0.02 0.06
MNOD-SI 0.2 0.21 0.42
Boosted-Histogram 037 0.25 0.663
TU-Darmstadt - - 0.489
Edinburg 0.19 0.002 0.00
INRIA-Dalal - 0.01 0.61
Figure 6: MNOD configuration used for the three categories
of objects in the dataset VOC2005. The model displays the
maps produced by each node C
P
and the features used in
input, all related to the input image of the testing set.
Figure 7: On the first line there are some image examples
of the dataset VOC2005. On the second line the maps pro-
duced by the trained model and the desired bounding box in
green.
object and its nodes may consist of different types
of neural learning strategies. This type of algorithm,
here mainly used for detection, provides an interest-
ing segmentation result that we intend to exploit in
future works.
We obtained good results on many standard
dataset compared to other object detection algorithms.
Moreover, the results show that our algorithm is ro-
bust to the change of perspective for the same object
and at the same time, it is robust for objects of the
LEARNING OBJECT DETECTION USING MULTIPLE NEURAL NETWORKS
135
0
0.2
0.4
0.6
0.8
1
0 0.2 0.4 0.6 0.8 1
precision
recall
Precision vs. Recall VOC2005 Dataset 1
cars
people
bicycles
Figure 8: PR curve for the three classes of objects bicycles,
people e cars. The model used for this graph is MNOD-SI.
same type but different forms in different poses or
even articulated and occluded.
The proposed algorithm suffers from some issues
related to datasets with conspicuous differences of
scale for the objects that we want to detect. Therefore
we are working on a different strategy to overcome
this problem. Detection results are dependent on net-
work topology and from the selected set of features.
Then, we are analyzing new search algorithms able to
select the best network configuration.
REFERENCES
Bouchard, G. and Triggs, B. (2005). Hierarchical part-
based visual object categorization. In Proc. CVPR,
pages 710–715.
Crandall, D., Felzenszwalb, P., and Huttenlocher, D. (2005).
Spatial priors for part-based recognition using statisti-
cal models. In Proc. CVPR, pages 10–17.
Csurka, G., Dance, C. R., Fan, L., Willamowski, J., and
Bray, C. (2004). Visual categorization with bags of
keypoints. In In Workshop on Statistical Learning in
Computer Vision, ECCV, pages 1–22.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In Proc. CVPR, pages
886–893.
Everingham, M., Zisserman, A., Williams, C. K. I., Gool,
L. V., Allan, M., Bishop, C. M., Chapelle, O., Dalal,
N., Deselaers, T., Dork, G., Duffner, S., Eichhorn, J.,
Farquhar, J. D. R., Fritz, M., Garcia, C., Griffiths, T.,
Jurie, F., Keysers, D., Koskela, M., Laaksonen, J., Lar-
lus, D., Leibe, B., Meng, H., Ney, H., Schiele, B.,
Schmid, C., Seemann, E., Shawe-taylor, J., Storkey,
A., Szedmak, O., Triggs, B., Ulusoy, I., Viitaniemi,
V., and Zhang, J. (2005). The 2005 pascal visual ob-
ject classes challenge. In Selected Proceedings of the
First PASCAL Challenges Workshop.
Fei-fei, L. (2005). A bayesian hierarchical model for learn-
ing natural scene categories. In Proc. CVPR, pages
524–531.
Fergus, R., Perona, P., and Zisserman, A. (2003). Ob-
ject class recognition by unsupervised scale-invariant
learning. In Proc. CVPR, pages 264–271.
Fischler, M. and Elschlager, R. (1973). The representation
and matching of pictorial structures. Computers, IEEE
Transactions on, C-22(1):67 – 92.
Leibe, B. and Schiele, B. (2003). Interleaved object cate-
gorization and segmentation. In Proc. BMVC, pages
759–768.
Riedmiller, M. and Braun, H. (1993). A direct adap-
tive method for faster backpropagation learning: The
rprop algorithm. In IEEE INTERNATIONAL CON-
FERENCE ON NEURAL NETWORKS, pages 586–
591.
Riesenhuber, M. and Poggio, T. (1999). Hierarchical mod-
els of object recognition in cortex. Nature Neuro-
science, 2(11):1019–1025.
Schmid, C. (2006). Beyond bags of features: Spatial
pyramid matching for recognizing natural scene cat-
egories. In Proc. CVPR, pages 2169–2178.
Serre, T., Wolf, L., and Poggio, T. (2005). Object recog-
nition with features inspired by visual cortex. In
Proceedings of the Conference on Computer Vision
and Pattern Recognition, CVPR ’05, pages 994–1000,
Washington, DC, USA. IEEE Computer Society.
Sharkey, A. J. (1999). Combining Artificial Neural Nets:
Ensemble and Modular Multi-Net Systems, chapter
Multi-Net Systems. Springer.
Todorovic, S. and Ahuja, N. (2006). Extracting subimages
of an unknown category from a set of images. In Proc.
CVPR, pages 927–934.
Utgoff, P. E. (1988). Perceptron trees: A case study in hy-
brid concept representations. In AAAI, pages 601–606.
Zhu, L. and Yuille, A. (2006). A hierarchical compositional
system for rapid object detection. In Proc. NIPS.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
136
