
COMBINED BLIND EQUALIZATION AND CLASSIFICATION
OF MULTIPLE SIGNALS
Barathram Ramkumar and Tamal Bose
Wireless@VT, Bradley Department of Electrical and Computer Engineering, Virginia Tech, Blacksburg, U.S.A.
Keywords:
Multiuser automatic modulation classifier (MAMC), Cumulants, MIMO blind equalizer.
Abstract:
A multiuser automatic modulation classifier (MAMC) is an important component of a multiantenna cogni-
tive radio (CR) receiver that helps the radio to better utilize the spectrum. MAMC identifies the modulation
schemes of multiple users in a frequency band simultaneously. A multi-input-multi-output (MIMO) blind
equalizer is another important component of a multiantenna CR receiver that improves symbol detection per-
formance by reducing inter symbol interference (ISI) and inter user interference (IUI). In a CR scenario, it
is preferable to also consider the performance of the automatic modulation classifier (AMC) while designing
the blind equalizer. In this paper we propose a MIMO blind equalizer that improves the performance of both
multiuser symbol detection and cumulant based MAMC.
1 INTRODUCTION
Cognitive radio (CR), introduced by Mitola (Haykin,
2005), is an emerging technology that has a wide
range of military and civilian applications. For a
CR operating military and public safety applications,
there is no information available to the radio about
signals present in the frequency band. AMC is a sig-
nal processing component that helps the CR identify
the modulation format employed in the detected sig-
nal. Most of the AMC algorithms in the literature
can classify only a single user present in a frequency
band. The authors of this paper recently proposed
a fourth order cumulant based MAMC in (Ramku-
mar and Bose, 2010b). The MAMC proposed in
(Ramkumar and Bose, 2010b) requires multiple re-
ceiving antennas. The MAMC was developed for
a more realistic multipath channel and no assump-
tion about the transmission powers of the user was
made. With multiple transmitting users and multiple
receiving antennas, the overall setup can be viewed
as a classical multiple input multiple output (MIMO)
communication system and is depicted in Figure 1.
Thus by using multiple receiving antennas apart from
classifying signals from multiple users, the CR re-
ceiver can harness the benefits offered by traditional
MIMO schemes. A novel blind MIMO channel es-
timation scheme is also proposed (Ramkumar and
Bose, 2010b) which forms a integral part of the pro-
posed multiuser AMC (refer to the block diagram of
the MAMC in Figure 2).
Due to the presence of multiple signals in a fre-
quency band, any transmitted signal is subjected to
inter userinterference (IUI). Also, the transmitted sig-
nals are subjected to inter symbol interference (ISI)
due to multipath fading. Since there is no training
sequence available in a CR scenario, MIMO blind
equalizers are used to remove IUI and ISI. Both sec-
ond order statistics (SOS) and higher order statistics
(HOS) of the received signal are required to acheieve
MIMO blind equalization. Since HOS are used,
MIMO blind equalizers have the potential to converge
to a local minimum. Convergence of MIMO blind
equalizer to local minimum not only affects symbol
detection performance but also the performance of
the MAMC. Typically, blind equalizers are designed
to improve the symbol detection performance. In a
CR, AMC is an important component and hence it
is better to design a blind equalizer that improves
the performance of both AMC and symbol detec-
tion. Two works in this direction are found in the
literature. However, both works consider only a sin-
gle user AMC and single input single output (SISO)
blind equalizer. The first work is in (Wu and Wu,
2008), where a robust switching SISO blind equalizer
is proposed that improves the performance of single
user AMC. In the second work (Ramkumar and Bose,
2010a), the weights of the SISO blind equalizer are
adapted in such a way that performance of the cumu-
lants based single user is improved.
339
Ramkumar B. and Bose T..
COMBINED BLIND EQUALIZATION AND CLASSIFICATION OF MULTIPLE SIGNALS.
DOI: 10.5220/0003331003390344
In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2011), pages
339-344
ISBN: 978-989-8425-48-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

In this paper we propose a MIMO blind equal-
izer that improves the performance of both multiuser
symbol detection and MAMC that was proposed in
(Ramkumar and Bose, 2010a). In order to do so,
we design a cost function that is related to the per-
formance of the multiuser AMC and then choose the
parameters of the blind equalizer such that the cost
function is maximized. The overall block diagram of
the proposed CR receiver is shown in Fig. 1. In the
figure, we design the MIMO blind equalizer G(z
−1
)
by considering the performance of both symbol de-
tection and MAMC. For designing the blind equalizer
we also use the MIMO channel estimates provided by
the MAMC.
The paper is organized as follows. In Section 2,
we provide the channel assumptions and background
theory. In Section 3, we briefly describe MAMC from
(Ramkumar and Bose, 2010b). The cost function re-
lated to the performance of the MAMC is also devel-
oped in this section. In Section 4, we present the step
by step procedure to design the MIMO blind equal-
izer. Simulation results are presented in Section 5,
followed by the conclusion.
Blind Equalizer
G(z
!1
)
Multiuser
AMC
Symbol
Detection
Blind Equalizer
Design
A
n
t
e
n
n
a
s
Proposed Cognitive Radio Receiver
User 1
User 2
User l
r
m
r
1
Figure 1: Block diagram of the proposed system.
2 BACKGROUND AND THEORY
As mentioned earlier, multiple receiving antennas are
used for classifying signals from multiple users. Let
l be the number of transmitting users and m be the
number of receiving antennas and it is required that
m > l. Usually in a CR scenario, l is not known and
needs to be estimated using algorithms like the one
proposed in (Shi and Su, 2007). The multipath chan-
nel between the j
th
user and i
th
receiving antenna is
denoted as h
ij
(z
−1
) and is given by
h
ij
(z
−1
) = h
ij
(0) + h
ij
(1)z
−1
+ ... + h
ij
(L)z
−L
, (1)
where L is the number of multipath components, z
−1
is the unit delay operator and h
ij
(k) (for k = 1, . . . ,L)
is the fading coefficients of the corresponding multi-
paths. The overall system can now be represented by
the following model
y(i) = x(i) + w(i), i = 0, 1,2, . . . (2)
x(i) = H(z
−1
)s(i),
where s(i) is the l × 1 transmission vector whose ele-
ments s
k
(i) (k = 1,2. . . l) denote the k
th
transmitting
user, y(i) is the m×1 reception vector whose elements
y
k
(i) (k = 1, 2.. . m) denote the received signal at the
k
th
receiving antenna, w(i) denotes the m × 1 noise
vector and H(z
−1
) is given by
H(z
−1
) =
h
11
(z
−1
) .. . h
1l
(z
−1
)
.
.
.
.
.
.
.
.
.
h
m1
(z
−1
) .. . h
ml
(z
−1
)
. (3)
Another representation of H(z
−1
) used in this paper
is
H(z
−1
) =
L
∑
k=0
H
k
z
−k
(4)
where H
k
(for k = 1, 2. . . L) is the m × l scalar ma-
trix. We make the following assumptions regarding
the system model (2).
Assumption 1: rank[H(z
−1
)] = l, for all complex z 6=
0, i.e. H(z
−1
) is irreducible.
Assumption 1 is valid for any practical wireless
channel with reasonable spatial diversity. Also we as-
sume that the signals transmitted by various users are
uncorrelatedand each element of the noise vector w(i)
is zero mean white Gaussian with variance σ
2
w
.
MIMO blind equalizers are used to recover the
transmitted signal vector s(i) using only the received
signal vector y(i) with no training sequence and
knowledge of the channel transfer function H(z
−1
).
As mentioned earlier, in this paper we design a blind
equalizer that takes into consideration the perfor-
mance of the multiuser AMC. In order to do so, we
consider the following theorem from (Tugnait, 1996).
Theorem 1:(Tugnait, 1996) For the system given in
(2) under Assumption 1 there exists (l × m) polyno-
mial matrix G(z
−1
) (not unique) such that
G(z
−1
)H(z
−1
) = I
l
. (5)
Since G(z
−1
) is not unique, we can choose G(z
−1
)
such that both symbol detection performance and
MAMC performances are improved.
According to (Kailath, 1979) (Tugnait and Huang,
2000), G(z
−1
) in (5) can be factorized as follows
G(z
−1
) = G
2
(z
−1
)G
1
(z
−1
), (6)
where G
2
(z
−1
) is a l × m polynomial matrix and
G
1
(z
−1
) is an arbitrary m× m polynomial matrix with
the condition det[G
1
(z
−1
)] 6= 0, for |z| ≥ 1. Since
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
340

G
1
(z
−1
) is an arbitrary polynomial matrix, we design
G
1
(z
−1
) such that the AMC performance is improved.
To do so, we first construct a cost function J
amc
which
is related to the performance of the multiuser AMC.
We then choose the parameters of G
1
(z
−1
) such that
J
amc
is maximized. The overall design of G
1
(z
−1
) can
be viewed as the following constrained optimization
problem
max
G
1
(z
−1
)
J
amc
s.t. det[G
1
(z
−1
)] 6= 0, for |z| ≥ 1 (7)
The rest of the paper is about formulating the cost
function J
amc
and solving for the polynomial matri-
ces G
1
(z
−1
) and G
2
(z
−1
).
3 MULTIUSER AMC AND COST
FUNCTION
In this section we briefly describe the multiuser AMC
from (Ramkumar and Bose, 2010b). Normalized
fourth order cumulants were used as a feature for mul-
tiuser AMC. For a complex random signal v(n), one
of the normalized fourth order cumulants is given by
˜
C
40v
=
C
40v
(C
21v
)
2
, (8)
where
C
21v
= E(|v|
2
) and C
40v
= E(v
4
) − 3E(v
2
)
2
(9)
For the multiuser system defined by (2), the rela-
tionship between the normalized cumulant values of
each transmitting user and normalized cumulant val-
ues of the signals received at each receiving antenna
is given by
˜
C
40y
1
.
.
.
˜
C
40y
m
=
γ
11
∆
2
1
...
γ
1l
∆
2
1
.
.
.
.
.
.
.
.
.
γ
m1
∆
2
m
...
γ
ml
∆
2
m
˜
C
40s
1
.
.
.
˜
C
40s
l
(10)
or
~
C
40y
= B
~
C
40s
where
˜
C
40y
i
(for i = 1,2. . . m) are the normalized
cumulant values of the signals at each receiving
antenna,
˜
C
40s
i
(for i = 1, 2...l) are the normalized cu-
mulant values of the signals transmitted by each user,
γ
ij
=
L−1
∑
k=0
|h
ij
(k)|
4
( for i = 1, 2...m, (11)
j = 1, 2. . . l)
Classifier
Receiver
Cumulant
Feature
Extraction
(m x 1) received
signal
Blind Channel
Estimation
AMC
Decision
Estimate the
cumulant values of
the transmitting users
Signal Processing Block
Figure 2: Block diagram of the mutltiuser AMC (Ramku-
mar and Bose, 2010b).
and
∆
i
=
l
∑
p=1
L−1
∑
k=0
|h
il
(k)|
2
( for i = 1, 2...m). (12)
In (Ramkumar and Bose, 2010b), a blind MIMO
channel estimation algorithm is proposed for estimat-
ing H(z
−1
). Using the estimated channel, the ele-
ments of the B matrix are computed. Using the es-
timated B matrix we solve for
~
C
40s
, which is used
as a feature for classification. The overall block di-
agram of the MAMC is shown in Figure 2. In Fig-
ure 2, the signal processing block extracts the fea-
tures
~
C
40s
which in turn is fed to the classifier. Some
of the widely used classifiers are neural networks,
support vector machines etc. In (Ramkumar and
Bose, 2010b), classifier used was the shortest distance
method. Refer to (Ramkumar and Bose, 2010b) for a
detailed explanation.
3.1 Cost Function for the Multiuser
AMC
In this subsection we develop the cost function J
amc
for designing blind equalizer polynomials G
1
(z
−1
)
and G
2
(z
−1
). In order to so, we need to understand
the effect of the MIMO FIR filter on the normalized
cumulant values of the receivedreceived signal. From
(10) one can see that the normalized cumulant values
of each received signal
˜
C
40y
i
(for i = 1, 2...m) is a
weighted sum of the normalized cumulant values of
all the transmitting users. The weighting coefficients
are given by w
ij
=
γ
ij
∆
2
i
(for i= 1,2...m, j= 1,2...l) (re-
fer to (10)). It can be easily shown that
|w
ij
| = |
γ
ij
∆
2
i
| < 1 ( for i = 1,2. . . m, (13)
j = 1, 2. . . l)
Since the magnitude of weighting coefficients are less
than one, the magnitude of the normalized cumulant
values of the received signals are driven towards zero.
The MIMO FIR channel clusters all the cumulant fea-
tures around zero. This clustering makes it hard for
COMBINED BLIND EQUALIZATION AND CLASSIFICATION OF MULTIPLE SIGNALS
341

the classifier shown in Figure 2 to distinguish between
the features. Thus the coefficients of the matrix poly-
nomial G
1
(z
−1
) must be chosen in such a way that the
features are unclustered. For this reason we propose
the following cost function
J
amc
=
m
∑
j=1
|C
40x
2j
|, (14)
where x
2
(i) = G
1
(z
−1
)y(i) and C
40x
2j
is the cumulant
value of the j
th
component in the vector signal x
2
(i).
The above cost function maximizes the magnitude of
the normalized cumulant values of the signals so that
the classifier can distinguish between the features.
4 DESIGNING THE MATRIX
POLYNOMIALS
In this section we propose the algorithm for design-
ing the polynomials G
1
(z
−1
) and G
2
(z
−1
). We also
present the overall step by step procedure for design-
ing the blind equalizer. The cost function in (14) can
be expressed as follows
J
amc
=
m
∑
j=1
|C
40x
2j
| = J
1
+ . . . + J
m
, (15)
where J
i
= |C
40x
2i
| (for i = 1. . . m). Now we choose
G
1
(z
−1
) to be the diagonal matrix given by
G
1
(z
−1
) = diag
C
1
(z
−1
),... ,C
m
(z
−1
)
, (16)
where the elements of diagonal matrix are the FIR fil-
ters given by
C
p
(z
−1
) = c
p1
z
−1
+ . . . + c
pL1
z
−L1
( for (17)
p = 1.. . m)
where L1 is the length of the filter and c
ij
(for i =
1, . . . , m, j = 1, . . . , L1) are the filter weights. Since
G
1
(z
−1
) is chosen to be a diagonal matrix, the con-
straint on G
1
(z
−1
) (refer to (7)) implies that the FIR
filter C
p
(z
−1
) (for p = 1. . . m) must be minimum
phase. That is the filter must not have any zeros on or
outside the unit circle. Let us denote the weight vec-
tor as c
p
= [c
p1
,...,c
pL
] (for p = 1, . . . , m), then we
use the following constrained gradient search tech-
nique for updating the weights. Due to the constraint
on G
1
(z
−1
) we restrict the search space to the region
where the weights form a minimum phase polyno-
mial. Let c
p
(k) denote the coefficient vector during
the iteration k = 0,1, 2, . . ..
• Step 1. For k = 0 initialize c
p
(0) to a random
value from the search space.
• Step 2. For k = 1, 2, . . . calculate the output of the
filter
x
2p
(n) =
L
∑
m=0
c
p
(m)y
p
(n− m) ( for (18)
p = 1.. . m)
• Step 3. Update the coefficient vector using the
following equation
c
p
(k) = c
p
(k− 1) − µ
∂J
p
∂c
p
for p = 1...m (19)
where µ is step size. The weights are updated only
if the new weights lies in the search space. If not,
repeat step 2.
• Step 4. If
|J
p
(c
p
(k))−J
p
(c
p
(k−1))|
J
p
(c
p
(k−1))
< ζ terminate the
iteration and go to step 5. If not, repeat step 2,
where ζ is chosen to be a small number less than
one.
• Step 5. Calculate the output x
2
(i) using G
1
(z
−1
).
Now the cumulant features of the (m× 1) signal vec-
tor x
2
are maximized and not clustered around zero,
therefore x
2
is given to the MAMC shown in Fig. 2
for classification. Let us denote
F(z
−1
) = G
1
(z
−1
)H(z
−1
) =
L+L1−1
∑
k=0
F
k
z
−k
. (20)
It can be seen from Fig. 2, that a blind MIMO channel
estimator forms an integral part of the MAMC. Here
we are not repeating the channel estimation algorithm
(refer to (Tugnait, 1996) for a detailed explanation).
Since x
2
(i) is fed to the MAMC, we obtain the esti-
mate of the polynomial F(z
−1
). Using the estimate of
F(z
−1
), we design G
2
(z
−1
) by solving the following
equation
G
2
(z
−1
)F(z
−1
) = I
l
, (21)
where I
l
is the (l × l) identity matrix. Let us denote
G
2
(z
−1
) as
G
2
(z
−1
) =
L2−1
∑
k=0
G
2k
z
−k
, (22)
where G
2k
(for k = 0,2. . . (L2 − 1)) are the l × m
scalar matrix. Now the solution to (21) is given by
(Tugnait, 1996)
G
21
G
22
G
23
... ...
=
I
l
...
S
†
, (23)
where S
†
is the pseudo inverse of the S matrix given
by
S =
F
0
F
1
F
2
... . . .
0 F
0
F
1
... . . .
.
.
.
.
.
.
.
.
.
.
.
. ...
0 0 0 F
0
...
. (24)
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
342

4.1 Overall Classification
and Equalization Algorithm
In this subsection we present the step by step imple-
mentation of the overall proposed system.
• Step 1. Given the (m× 1) received signal vector
y(i) estimate the number of transmitting users l
using the method proposed in (Shi and Su, 2007).
• Step 2. Choose the length of the matrix polynomi-
als L1 and L2. Since the length of the channel im-
pulse response is not known, choose a sufficiently
large length so that the system is over modeled.
• Step 3. G
1
(z
−1
) is chosen to be a diagonal matrix
given by (16) and its coefficients are adapted using
the gradient search algorithm given by (19).
• Step 4. The signal x
2
(i) is sent to the MAMC for
classification. The MAMC provides an estimate
of the matrix polynomial F(z
−1
).
• Step 5. Using the estimated F(z
−1
), design the
(l × m) matrix polynomial G
2
(z
−1
) by solving
(21). The output of G
2
(z
−1
) is used for symbol
detection.
5 PERFORMANCE ANALYSIS
In this section, we demonstrate the performance of the
proposed MIMO blind equalizer using Monte Carlo
simulation. Since the performance of the MAMC is
also considered while designing the blind equalizer,
we analyze the performance of both the MAMC and
symbol detection. For the Monte Carlo simulation,
1,000 trials are considered.
5.1 MAMC Performance
In this subsection we demonstrate the performance of
the MAMC using computer simulation. The perfor-
mance measure considered is the probability of cor-
rect classification P
cc
. Suppose that there are l users
and M modulation schemes which are denoted as
Ω = {Ω
1
,... , Ω
M
}. Then there are L
1
= M
l
possible
transmission scenarios denoted as D = {d
1
,... , d
L
1
}.
The probability of correct classification P
cc
is defined
as
P
cc
=
L
1
∑
i=1
P(d
i
|d
i
)P(d
i
) (25)
where P(d
i
) is the probability that the particular trans-
mission scenario occurs and P(d
i
|d
i
) is the correct
classification probability when scenario d
i
has been
transmitted. For the simulation we assume P(d
i
) =
1
L
1
,∀i, where all scenarios are equally probable.
5.1.1 Two User Three Class Problem
In this experiment we consider l = 2 transmitting
users and m = 3 receiving antennas. Each entry
of the 3 × 2 channel matrix is considered to be a
three tap FIR filter whose coefficients are chosen ran-
domly from a Gaussian distribution of unit variance.
Three modulation schemes are considered for this ex-
periment and they are Ω = {BPSK,QPSK, PSK(8)}.
Since three modulation schemes are considered, there
are nine possible scenarios. The Monte Carlo simula-
tion results are summarized in Figure 3. In Figure 3,
the curve labeled P
cc1
shows the performance of the
MAMC without the proposed blind equalizer. The
curve labeled P
cc2
illustrates the performance of the
AMC using the proposed system.
−4 −2 0 2 4 6 8 10
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
SNR
Probablity of correct classification
Pcc2
Pcc1
Figure 3: Performance of the MAMC (Two user three class
problem).
5.1.2 Two User Four Class Problem
This problem is the same as the previous one
except four modulation schemes are considered.
The modulation schemes considered are Ω =
{BPSK,QAM(4), QAM(64),PSK(8)}. The Monte
Carlo simulation results are summarized in Figure 4.
In Figure 4 the curves labeled P
cc1
, and P
cc2
have the
same meaning as that of Figure 3.
−4 −2 0 2 4 6 8 10
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
SNR
Probablity of correct classification
Pcc2
Pcc1
Figure 4: Performance of the MAMC (Two user four class
problem).
From Figure 3 and Figure 4 it can be seen that the
proposed MIMO blind equalizer enhances the perfor-
mance of the MAMC.
COMBINED BLIND EQUALIZATION AND CLASSIFICATION OF MULTIPLE SIGNALS
343
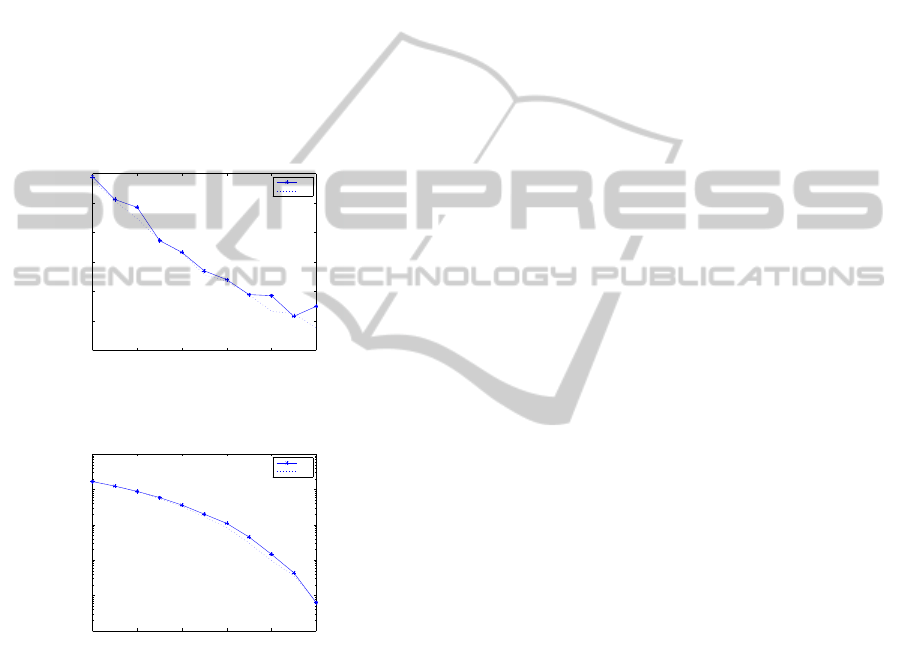
5.2 Symbol Detection Performance
In order to analyze the symbol detection performance,
we consider the same 2-input/3-output FIR random
channel considered in the previous experiment. The
normalized mean square error (NMSE) and symbol
error rate (SER) are taken as performance measures.
The simulation results are shown in Figure 5 and Fig-
ure 6. In Figure 5 and Figure 6 the curve labeled sd1
illustrates the symbol detection performance of the
proposed system. The curvelabeled sd2 illustrates the
symbol detection performance of equalizer when the
channel impulse response is known (non-blind equal-
izer). From the figures it can be seen that the symbol
detection performance of the proposed system is close
to that of the non-blind MIMO equalizer.
0 2 4 6 8 10
−12
−11
−10
−9
−8
−7
−6
SNR
NMSE
sd1
sd2
Figure 5: Symbol detection performance of the proposed
system (NMSE Vs SNR).
0 2 4 6 8 10
10
−5
10
−4
10
−3
10
−2
10
−1
10
0
SNR
SER
sd2
sd1
Figure 6: Symbol detection performance of the proposed
system (SER Vs SNR).
6 CONCLUSIONS
In this paper we designed a MIMO blind equal-
izer that improves the performance of both cumu-
lant based MAMC and symbol detection. The per-
formance of proposed equalizer was analyzed using
computer simulations and yielded promising results.
Future work is to extend this concept to cyclic cumu-
lant based MAMC.
ACKNOWLEDGEMENTS
This work was supported in part by the Institute for
Critical Technology and Applied Sciences.
REFERENCES
Haykin, S. (2005). Cognitive radio: Brain-empowered
wireless communications. In IEEE J. Sel. Areas Com-
mun. IEEE.
Kailath, T. (1979). Linear systems. Prentice Hall.
Ramkumar, B. and Bose, T. (2010a). Robust automatic
modulation classification and blind equalization: A
novel cognitive receiver. In Proc. of Wireless Inno-
vation Forum. SDR Forum.
Ramkumar, B. and Bose, T. (2010b). Robust multiuser auto-
matic modulation classifier for multipath fading chan-
nels. In in Proc. IEEE Dyspan. IEEE.
Shi, M. and Su, W. (2007). Adaptive estimation of the num-
ber of transmit antennas. In in Proc. IEEE MILCOM.
IEEE.
Tugnait, J. (1996). Fir inverse to mimo rational transfer
functions with applications to blind equalization. In
13th Asilomar Conference on Signals, Systems and
Computers. IEEE.
Tugnait, J. and Huang, B. (2000). On a whitening approach
to partial channel estimation and blind equalization
of fir/iir multiple-input multiple-output channels. In
IEEE Trans. Signal Process. IEEE.
Wu, H. and Wu, Y. (2008). Robust switching blind equal-
izer for wireless cognitive receivers. In IEEE Trans.
Wireless Commun. IEEE.
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
344
