
TOWARDS K-SET FRAMEWORKS IN EDUCATION
Mark Sh. Levin
Inst. for Inform. Transmission Problems, Russian Acad. of Sci., 19 Bolshoj Karetny lane, Moscow, Russia
Keywords:
Problem structuring, Problem solving, Decision making, Combinatorial optimization, Education.
Abstract:
The paper addresses k-set frameworks as a basic for education (teaching and students projects). The material
consists of the following: (i) scheme of designing a structural description for a new domain (as a new .world.),
(ii) k-set problems (one-set problems as decision making/ordering, two-set problems as assignment/allocation,
etc.), (iii) problems of hierarchy design and restructuring/reconfiguration (hierarchical clustering, spanning
trees, reconfiguration of spanning trees), (iv) combined frameworks (decision making framework, framework
for system testing/maintenance, planning in distributed computer environment), and (v) educational scheme
based on k-set problems/frameworks.
1 INTRODUCTION
In recent decades, the significance of complex sys-
tems and complex problems in education has been
increased. Thus, contemporary student education
has to lead to multidimensional system thinking in-
cluding the following: (1) multi-component sys-
tems, (2) multi-stage system life cycle, (3) multicrite-
ria/multiparameter approaches, (4) multilevel scales
for evaluation, (5) multi-method (multi-disciplinary)
approaches, (6) multi-model approaches, and (7)
structural approaches and methods. In general, it is
reasonable to point out that problem structuring phase
is often a crucial one in problem life cycle (i.e., prob-
lem description, problem statement, problem solving,
etc.). In recent years, problem structuring methodol-
ogy is intensively studied (Keys, 2007; Rosenhead,
2006; White, 2009; Wiek and Walter, 2009).
k-set frameworks were suggested for structuring
and formulation of complex multi-component applied
domains in (Levin, 2010b). Here k-set frameworks
are considered as a basic for education (teaching and
students projects). Mainly the material has a discus-
sion character. The following is considered:
(i) scheme of designing a structural description for
a new domain (as a new “world”),
(ii) k-set problems (one-set problems as deci-
sion making/ordering, two-set problems as assign-
ment/allocation, etc.),
(iii) problems of hierarchy design and restructur-
ing/reconfiguration (hierarchical clustering, spanning
trees, reconfiguration of spanning trees),
(iv) combined frameworks (decision mak-
ing framework, framework for system test-
ing/maintenance, planning in distributed computer
environment), and
(v) educational scheme based on the prob-
lems/frameworks above.
2 DESIGN OF A NEW WORLD
A basic preliminary stage of problem structur-
ing/formulation (design of a new “world”) consists in
the following:
Stage 1. Revelation of basic concepts (e.g., goals,
objects, resources).
Stage 2. Revelation of relations (relations over the
concepts at the same concept set, relations over the
concepts of different concept sets).
Stage 3. Formulation of main problems (e.g., re-
source assignment, planning, scheduling).
Figure 1 depicts the design approach to a new
“world” including concept sets and relations. Further,
it is possible to consider solving scheme, solving pro-
cess, and analysis of results.
3 K-SET PROBLEMS
Basic one-set problems are depicted in Figure 2. Here
the problem set consists of basic decision making
problems (choice, ranking/sorting, clustering) (Levin,
1998; Levin, 2006a; Roy, 1996; Simon and Newell,
99
Sh. Levin M..
TOWARDS K-SET FRAMEWORKS IN EDUCATION.
DOI: 10.5220/0003335800990104
In Proceedings of the 3rd International Conference on Computer Supported Education (CSEDU-2011), pages 99-104
ISBN: 978-989-8425-50-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
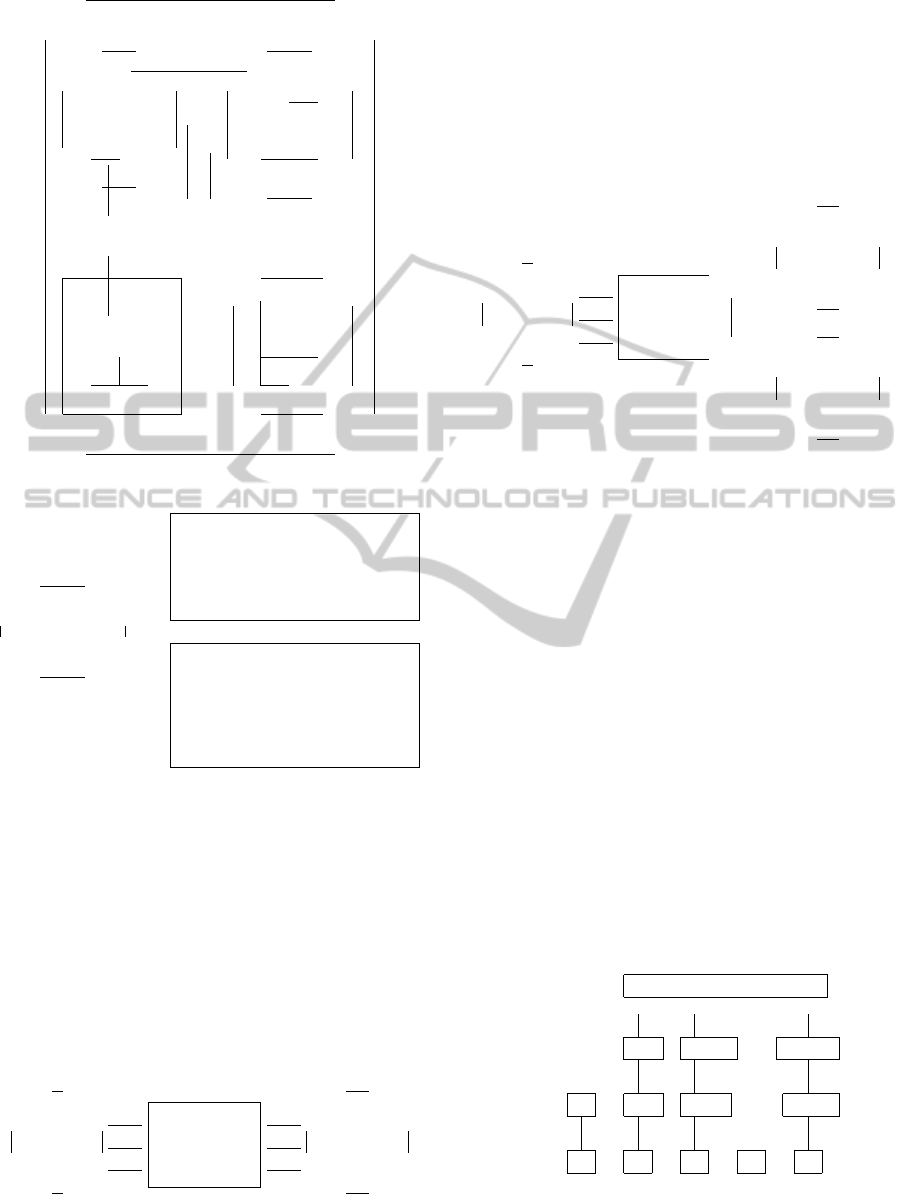
Figure 1: Illustration for new “world”.
'
&
$
%
Concept set 1
'
&
$
%
r
r
A
A
Ar
r r
H
H
H
External
relations
-
P
P
P
P
P
Pq
P
P
P
P
Pq
>
Concept set 2
'
&
$
%
q
q
c
c qc
@
@
qc
q qc c
H
H
HA
A
A
Internal
relations
r
r
e
e
re
re
@
@r re e
Concept set 3
@
@
@
@
t
t
H
H
H
t t
@
@t t
Concept set 4
Figure 2: One-set problems.
@
@R
'
&
$
%
Set of
elements/
alternatives
Decision making problems:
* choice,
* ranking/sorting,
* clustering
Combinatorial
optimization problems:
* ordering/scheduling,
* grouping,
* selection (e.g., knapsack)
1958; Zapounidis and Doumpos, 2002) and combina-
torial optimization problems as ordering/scheduling,
grouping, knapsack (i.e., selection of a subset) (Garey
and Johnson, 1979; Levin, 1998).
Generally, a set of two-set problems involves as-
signment/allocation problem, graph coloring (Figure
3) (Garey and Johnson, 1979; Levin, 1998; Levin,
2009a).
Figure 3: Illustration for two-set problems.
Set 1
(elements,
colors, etc.)
rr
r
r
r
r
'
&
$
%
Assignment,
allocation
-
-
-
Set 2 (e.g.,
positions)
c
c
c
c
c
c
c
c
c
c
'
&
$
%
Three-set problems are based of 3-matching (Fig-
ure 4) (Garey and Johnson, 1979; Levin, 2009a). In
addition, it may be reasonable to point out the fol-
lowing kind of problem (scheduling of assignment re-
sults): assignment problem (e.g., workers/tasks into
work positions/processors) at each time interval. Here
the set of time intervals corresponds to the third set.
Figure 4: Illustration for three-set problems.
Set 1
(elements)
rr
r
r
r
r
'
&
$
%
@
@
Matching
*
*
*
H
Hj
H
Hj
H
Hj
Set 2
(positions)
dr
d
d
r
r
d
d
r
r
d
d
r
r
'
&
$
%
Set 3 (e.g.,
time intervals)
c
c
c
c
c
c
c
'
&
$
%
4 HIERARCHY AND
RESTRUCTURING
In recent decades problems of “design of hierarchy”
over set element became to be a critical part of many
real world applications. This kind of problem corre-
sponds to revelation of binary relation(s) (as hierar-
chy) over a set of element. Note traditional decision
making problems (i.e., choice, ranking) and some
combinatorial optimization problems (e.g., knapsack,
multiple choice problem) may be considered as “de-
sign of hierarchy” because they are targeted to resul-
tant binary relations over alternatives/elements. Hier-
archical clustering (agglomerative algorithms) leads
to a tree-like structure (or a hierarchy) over a set of
initial elements (Figure 5). The agglomerative algo-
rithm implements a “Bottom-Up” solving scheme.
Figure 5: Scheme of agglomerative algorithm.
Step 0
1 2
3
4
5
Step 1
1
6
2, 3
6
3, 4
6
@
@I
@
@I
4, 5
6
Step 2
1
2, 3
6
6
1, 3, 4
6
6
3, 4, 5
6
6
*
1, 2, 3, 4, 5
. . .
CSEDU 2011 - 3rd International Conference on Computer Supported Education
100

Evidently, the examined problem may be based on
ex-pert judgment as well.
Problems of “spanning trees” (e.g., minimal span-
ning tree problem, Steiner tree problem, multicriteria
versions of the problems) can be considered as a spe-
cial class of the examined problems (i.e., “design of
hierarchy”). Figure 6 illustrates the problems.
Figure 6: Illustration for spanning trees.
Initial graph
s
C
C
C
C
C
C
@
@
@
s
s
J
J
J
J
J
s
s
H
H
H
s
Spanning tree
s
C
C
C
C
C
C
@
@
@
s
s
s
s
s
Steiner tree
s
s
sseA
A
A
s
s
s
A prospective problem kind consists in restructur-
ing (reconfiguration, resolving) of a structured prob-
lem solution (e.g., (Levin, 2009a)). This problem may
be used for the following basic combinatorial opti-
mization problems as a change of a solution (e.g.,
subset, structure): (i) knapsack problem, (ii) multiple
choice problem, (iii) assignment, (iv) graph coloring,
(v) vertex covering, (vi) spanning tree problem (Fig-
ure 7), (vii) Steiner problem (Figure 8). Here it is nec-
essary to take into account a cost of solution changes
(e.g., removal of a Steiner node).
Figure 7: Restructuring of spanning tree.
Initial
graph
s
C
C
C
C
C
C
@
@
@
s
s
J
J
J
J
J
s
s
H
H
H
s
Spanning
tree 1
s
C
C
C
C
C
C
@
@
@
s
s
s
s
s
=⇒
Spanning
tree 2
s
s
s
J
J
J
J
J
s
s
s
Let P be a combinatorial optimization problem
with a solution as structure S (i.e., subset, graph), A be
initial data (element parameters, etc.), f(P) be objec-
tive function(s). Thus S(A) will be a solution of initial
data A, f(S(A)) will be the corresponding objective
function. Further, let A
0
be initial data at an initial
stage, f(S(A
0
)) will be the corresponding objective
function, A
1
be initial data at next stage, f(S(A
1
)) will
be the corresponding objective function.
As a result, the following solutions can be consid-
ered: (a) S
0
= S(A
0
) with f(S(A
0
)) and (b)
Figure 8: Restructuring of Steiner tree.
Initial
graph
s
C
C
C
C
C
C
@
@
@
s
s
J
J
J
J
J
s
s
H
H
H
s
Steiner
tree 1
s
s
s
s
seA
A
A
s se
s
=⇒
Steiner
tree 2
s
s
se
@
@ sse
s
s
s
S
1
= S(A
1
) f(S(A
1
)). In addition it is reasonable to
examine a cost of changing a solution into another
one: c(S
α
→ S
β
). Let ρ(S
α
, S
β
) be a proximity be-
tween solutions S
α
and S
β
, for example, ρ(S
α
, S
β
) =
| f(S
α
) − f(S
β
)|. Note function f(S) is often a vec-
tor function. Finally, the restructuring problem can be
examine as follows (a basic version):
Find a solution S
ξ
while taking into account the
following:
(i) c(S
0
→ S
ξ
) → min and (ii) ρ(S
ξ
, S
1
) → min
(or constraint).
Figure 9 illustrates the suggested restructuring
problem.
Figure 9: Illustration for restructuring problem.
6
-
d
Initial
solution S
0
Z
Z
w
Goal
solution S
1
'
&
$
%
'
&
$
%
H
H
HY
H
H
Hj
Proximity
ρ(S
ξ
, S
1
)
Neighborhoods
of S
1
@
@
@
H
H
H
er
Obtained
solution S
ξ
X
X
Solution
change cost
c(S
0
→ S
ξ
)
@
@
5 COMBINED FRAMEWORKS
In recent sixteen years, the author and his students
have used several typical combined frameworks, for
example:
(i) hierarchical morphological design of modular
systems,
(ii) improvement of networked systems (including
improvement of system components, improvement of
interconnection among system components, improve-
ment of system structure), and
TOWARDS K-SET FRAMEWORKS IN EDUCATION
101
(iii) planning of marketing (including groups
of products, marketing strategies, typical customer
groups).
Here three combined problem solving frameworks
are illustrated.
5.1 Decision Making
A scheme of decision making process is depicted in
Figure 10 (Levin, 2006a). The scheme is an impor-
tant basis for teaching of decision making engineer-
ing. On the other hand, the scheme is a reference ex-
ample of a generalized applied domain. Here the fol-
lowing sets are basic ones: (i) criteria (and their im-
portance, relations over them), (ii) alternatives (and
their estimates upon criteria or relations), (iii) solv-
ing methods/techniques, (iv) experts, and (v) refer-
ence decisions.
Figure 10: Decision making framework.
Set of
alternatives
-
@
@
-
Decision(s)
@
@
@
@
Set of
criteria
H
H
H
Hj
Set of
techniques
*
Reference
decisions
?
@
@
Set of
experts
6
5.2 System Testing/Maintenance
Stages of system testing and system maintenance are
significant parts of system life cycle. In the case
of modular systems, planning of the stages above
can be based on a multi-set framework (Levin and
Merzlyakov, 2008) (Figure 11). Here the follow-
ing sets are examined: (a) set of workers, (b) set
of system components/parts, and (c) basic set of
test/maintenance actions. Clearly, time intervals can
be considered as well. Here two optimization prob-
lems are used: assignment/allocation (i.e., workers
into system parts) and multiple choice knapsack prob-
lem (selection of actions while taking into account a
total resource constraint).
5.3 Distributed Computing
Figure 12 illustrates planning in distributed comput-
ing environment that is based on the following sets:
(i) set of computer servers (including relations over
the servers), (ii) several sets of computing tasks (in-
cluding relations over the tasks), (iii) time intervals.
The main problem is:
Figure 11: System testing/maintenance.
Test/maintenance actions
Z
Z}
Workers
s
r
s
s
t
System
components
q
q
p
r
r
e
f
d
d
g
Q
Q
Q
Q
Q
Q
Q
Qs
P
P
P
P
P
P
P
Pq
3
:
Figure 12: Planning for distributed computing.
'
&
$
%
Computing
tasks
r r r r---
r r r r
-
@
@R
--
@
@R
'
&
$
%
Computing
tasks
q q q qc c c c
---
q q q qc c c c
@
@R---
. . .
'
&
$
%
Computing
tasks
r r r rc c c c---
r rc c
@
@R
-
Computer
environment
Servers
'
&
$
%
j
h
j
f
h
i
j
H
H
H
H
H
H
H
H
H
H
H
Hj
H
H
H
H
H
Hj
-
-
*
*
Task
assignment
Time intervals
-
t0
τ
1
τ
2
Assign computing tasks into servers(for each time
interval) while taking into account the following: (1)
relations over the tasks, (2) resource requirements of
each task, (3) relations over the servers, and (4) re-
sources of each server.
In addition, other combinatorial problems are
used, for example: grouping of tasks, selec-
tion/ranking of tasks and/or servers.
6 EDUCATIONAL SCHEME
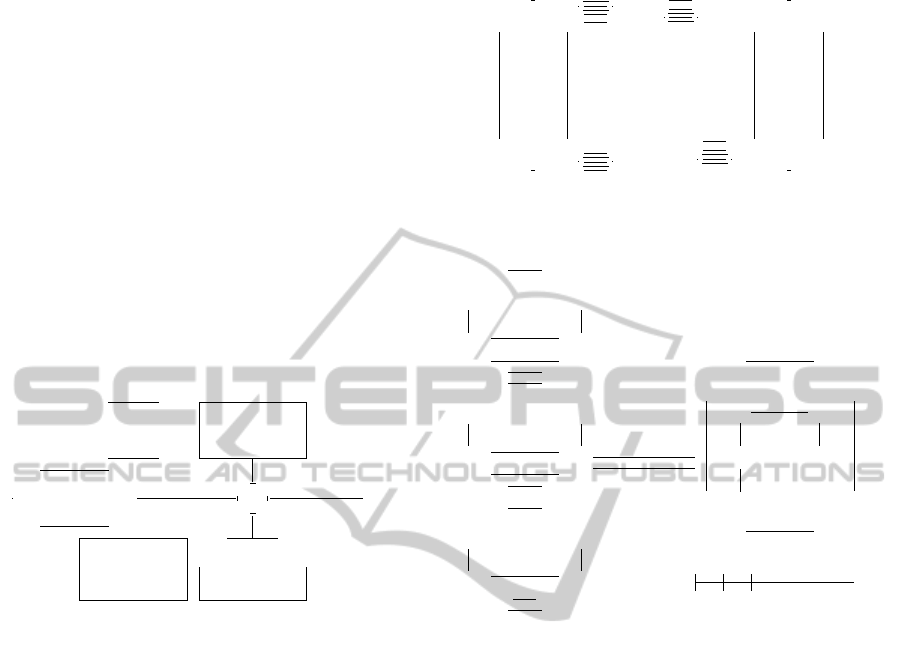
Our generalized educational framework is based on
a flow of k-set problems (Figure 13). The educa-
tional process is targeted to step-by-step examination
of more and more complicated problems/models (i.e.,
one-set problems, two set problems, and etc.). Con-
currently, students have to obtain the following infor-
mation and skills:
(a) models and algorithm (algorithm schemes,
solving procedures),
(b) real world applications (e.g., system design,
management, maintenance) in various domains (com-
puter systems, engineering, management, etc.).
CSEDU 2011 - 3rd International Conference on Computer Supported Education
102

In the best case, students can examine applica-
tion problems in the filed of their interests/experience
(e.g., communication systems, software engineering,
information systems, web-based services, private life,
sport).
Figure 13: Generalized educational framework.
Models,
algorithms/
procedures
(decision
making,
combinato-
rial optimi-
zation)
One-set
problems
???
-
Two-set
problems
???
-
Three-set
problems
???
-
Design of
hierarchy,
restructuring
???
-
Combined
frameworks
-
Applications
(system
design,
management,
maintenance,
testing, etc.)
7 CONCLUSIONS
In the paper, k-set frameworks are considered as a
basic for education (teaching and students projects).
The material of the article is based on authors course
and advising his undergraduateand graduate students:
Moscow Inst. of Physics and Technology - State
Univ., Faculty of Radio Engineering and Cybernetics
(Levin, 2006b; Levin, 2009b; Levin, 2010a). Over ten
students papers based on k-set problem frameworks
were published (Table 1):
1. 2-set framework (multicriteria assignment, sys-
tem upgrade based on multicriteria multiple choice
problem),
2. 3-set framework (system testing, marketing),
3. frameworks for spanning trees (multicriteria
Steiner tree problem, multicriteria Steiner tree prob-
lem with cost of Steiner vertices), and
4. framework for hierarchical system design.
In the future it may be reasonable to consider the
following research directions:
(i) study and usage of the modified k-set frame-
works and new kinds of the k-set frameworks;
(ii) consideration of the additional problem kinds
(e.g., covering problems, graph coloring problems);
(iii) examination of various restructuring prob-
lems/models and their applications;
(iv) continuation of educational activity as student
projects based on k-set frameworks;
Table 1: Students papers.
Kind of
framework
References
1. 2-set framework
(multicriteria
assignment,
system upgrade
based on
multicriteria
multiple choice
problem)
(Levin and Petukhov, 2010b)
(Levin and Safonov, 2010)
(Levin and Petukhov, 2010a)
2. 3-set framework
(system testing,
marketing)
(Levin and Merzlyakov, 2008)
(Levin and Fimin, 2009)
3. Frameworks for
spanning trees
(Levin and Nuriakhmetov, 2009)
(Levin and Zamkovoy, 2010)
4. Framework for
hierarchical
system design
(Levin and Vishnitskiy, 2007)
(Levin and Khodakovskii, 2007)
(Levin and Sharov, 2009)
(Levin and Fimin, 2010)
(v) usage of k-set problems and combined frame-
works as a basis for students evaluation/classification;
and
(vi) design of special computer-support environ-
ments based on k-set frameworks.
REFERENCES
Garey, M. R. and Johnson, D. S. (1979). Computers
and Intractability. The Guide to the Theory of NP-
Completeness. W.H.Freeman and Company, San
Francisco.
Keys, P. (2007). Knowledge work, design science and prob-
lem structuring methodology. Systems Research and
Behavioral Science, 24(5):523–535.
Levin, M. S. (1998). Combinatorial Engineering of Decom-
posable Systems. Kluwer, Dordrecht.
Levin, M. S. (2006a). Composite Systems Decisions.
Springer, New York.
Levin, M. S. (2006b). Course “system design: structural
approach”. In Proc. of 18th International Confer-
ence Design Methodology and Theory DTM2006, vol-
ume 4a. ASME.
Levin, M. S. (2009a). Combinatorial problems in system
configuration design. Automation and Remote Con-
trol, 70(3):519–561.
TOWARDS K-SET FRAMEWORKS IN EDUCATION
103

Levin, M. S. (2009b). Student research projects in system
design. In Proc. of International Conference on Com-
puter Supported Education CSEDU-2009, volume 2.
INSTICC.
Levin, M. S. (2010a). Course on system design (structural
approach). Information Processes, 10(4):303–324.
Levin, M. S. (2010b). Towards k-set frameworks in multi-
criteria combinatorial optimization. In Proc. of 11th
Symp. on Decision Technology and Intelligent Infor-
maiton Systems, volume XI. The Int. Inst. for Ad-
vanced Studies in Systems Research and Cybernetics.
Levin, M. S. and Fimin, A. V. (2009). Combinatorial
scheme for analysis of political candidates and their
strategies. Information Processes, 9(2):83–92 (in Rus-
sian).
Levin, M. S. and Fimin, A. V. (2010). Configuration of
alarm wireless sensor element. In Proc. of 2nd In-
ternational Congress on Ultra Modern Telecommuni-
cation and Control Systems and Workshops ICUMT-
2010. IEEE.
Levin, M. S. and Khodakovskii, I. A. (2007). Structural de-
sign of the telemetry system. Automation and Remote
Control, 68(9):1654–1661.
Levin, M. S. and Merzlyakov, A. O. (2008). Composite
combinatorial scheme of test planning (example for
microprocessor systems). In IEEE Region 8 Interna-
tional Conference Sibircon-2008. IEEE.
Levin, M. S. and Nuriakhmetov, R. I. (2009). Multicrite-
ria steiner tree problem for communication network.
Information Processes, 9(3):199–209.
Levin, M. S. and Petukhov, M. V. (2010a). Connection of
users with a telecommunications network: multicrite-
ria assignment problem. Journal of Communications
Technology and Electronics, 55(12):1532–1542.
Levin, M. S. and Petukhov, M. V. (2010b). Multicriteria
assignment problem (selection of access points). In
Proc. of 23rd International Conference on Ind. Eng.
& Other Appllications of Appl. Intell. Syst. IEA/AIE
2010, volume LNCS 6097, part II. Springer-Verlag.
Levin, M. S. and Safonov, A. V. (2010). Towards mod-
ular redesign of networked system. In Proc. of 2nd
International Congress on Ultra Modern Telecommu-
nication and Control Systems and Workshops ICUMT-
2010. IEEE.
Levin, M. S. and Sharov, S. Y. (2009). Hierarchical morpho-
logical composition of web-hosting system. Journal
of Integrated Design and Process Science, 13(1):1–
14.
Levin, M. S. and Vishnitskiy, R. O. (2007). Towards mor-
phological design of gsm network. Information Pro-
cesses, 7(2):183–190.
Levin, M. S. and Zamkovoy, A. A. (2010). Multicriteria
steiner tree with cost of vertices. In Proc. of 7th Inter-
national Conference CAD/CAM/PDM-2010. Inst. of
Control Problems.
Rosenhead, J. (2006). Past, present and future of problem
structuring methods. Journal of the Operational Re-
search Society, 57(7):759–765.
Roy, B. (1996). Multicriteria Methodology for Decision
Aiding. KLuwer, Dordrecht.
Simon, H. A. and Newell, A. (1958). Heuristic problem
solving: The next advance in operations research. Op-
erations Research, 6(1):1–10.
White, L. (2009). Understanding problem structuring meth-
ods interventions. European Journal of Operational
Research, 199(3):823–833.
Wiek, A. and Walter, A. I. (2009). A transdisci-
plinary approach for formalized integrated planning
and decision-making in complex systems. European
Journal of Operational Research, 197(1):360–370.
Zapounidis, C. and Doumpos, M. (2002). Multicriteria
classification and sorting methods: A literature re-
view. European Journal of Operational Research,
138(2):229–246.
CSEDU 2011 - 3rd International Conference on Computer Supported Education
104
