
EVALUATION OF COLLABORATIVE FILTERING ALGORITHMS
USING A SMALL DATASET
Fabio Roda, Leo Liberti
LIX,
´
Ecole Polytechnique, 91128 Palaiseau, France
Franco Raimondi
School of Engineering and Information Sciences, Middlesex University, London, U.K.
Keywords:
Recommender systems, TMW, KNN.
Abstract:
In this paper we report our experience in the implementation of three collaborative filtering algorithms (user-
based k-nearest neighbour, Slope One and TMW, our original algorithm) to provide a recommendation service
on an existing website. We carry out the comparison by means of a typical metric, namely the accuracy
(RMSE). Usually, evaluations for these kinds of algorithms are carried out using off-line analysis, withholding
values from a dataset, and trying to predict them again using the remaining portion of the dataset (the so-called
“leave-n-out approach”). We adopt a “live” method on an existing website: when a user rates an item, we also
store in parallel the predictions of the algorithms on the same item. We got some unexpected results. In the
next sections we describe the algorithms, the benchmark, the testing method, and discuss the outcome of this
exercise. Our contribution is a report of the initial phase of a Recommender Systems project with a focus on
some possible difficulties on the interpretation of the initial results.
1 INTRODUCTION
Recommender systems have became an important re-
search area in the field of information retrieval; many
approaches have been developed in recent years and
many empirical studies appeared. Evaluation of most
works has been carried out using “artificial” dataset
provided by well know research groups, such as
GroupLens, or by the Netflix prize. This situation
assures somehow a standard in the way results are
evaluated but also can lead to tuning the algorithms
to work better with dataset which have specific fea-
tures. In general, from the practitioner’s point of view,
there is a lack of precise delimitation for the domain
of applicability of algorithms and it is not totally clear
which is the minimal size of a dataset for a certain al-
gorithm. Small and poor datasets can “waste” good
algorithms; in addition, most algorithms are likely
to have very similar performance on these kinds of
dataset, thus rendering initial design choices very dif-
ficult. The aim of this paper is to provide elements of
discussion on this subject.
To ground our claims we make use of a concrete
online application which suggests places in the real
world (restaurants, bars, shops, etc) to registered
users, trying to match users’ tastes by digging into the
network of friends and places of the community to get
the best possible responses. Using an accepted termi-
nology (Vozalis and Margaritis, 2003), we can clas-
sify the application as a Collaborative Filtering Sys-
tem. We have implemented our in-house algorithm
for this application, called TMW, which tries to over-
come the issue of fragmented information, and we
have compared it to two classical algorithms: user-
based k-nearest neighbour and Slope One. These
three algorithms constitute the base for the experi-
mental evaluation presented in this paper.
The reminder of this paper is organised as follows.
In Section 2 we describe the three algorithms. In
Section 3 we report the experimental results obtained
when running these algorithms on a production envi-
ronment. In Section 4 we discuss the results.
2 BACKGROUND
In this section we describe the algorithms used for the
evaluation: k-nearest neighbour (KNN), Slope One,
603
Roda F., Liberti L. and Raimondi F..
EVALUATION OF COLLABORATIVE FILTERING ALGORITHMS USING A SMALL DATASET.
DOI: 10.5220/0003336506030606
In Proceedings of the 7th International Conference on Web Information Systems and Technologies (WEBIST-2011), pages 603-606
ISBN: 978-989-8425-51-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

and TMW. For a given user u and a given item (place)
i we denote with Pr(u, i) the outcome of the algorithm
(the prediction).
2.1 KNN
In the well known KNN approach to collaborative
filtering (Breese et al., 1998), input data are expressed
by a matrix R, where each entry r
ui
represents the
rating of user u for item i. Rows and columns
(representing users or items) are compared to identify
“similarities”. Especially in the so called “user
based” approach we look for correlation between
users. Indeed, users who rate the same items in a
similar way form a “Neighborhood” (we call them
“mentors”) that we can use to estimate a prediction.
We use a to identify the “active user” (the one we
want to anticipate) and sim
au
the similarity between
the active user a and a generic user u. The simplest
way to use the mentors’ ratings is a weighted average,
so the prediction function is:
prediction(a, i) =
∑
u
r
ui
∗sim
au
∑
u
|sim
au
|
There are many ways to compute the similarity
between users, for example, a well-established tech-
nique is “Cosine Similarity”. The similarity between
two users, u, and a, is obtained by calculating the co-
sine of the angle formed between the corresponding
vectors (rows in the matrix).
cosine similarity =
∑
i
r
ui
∗r
ai
√
∑
i
r
2
ui
√
∑
i
r
2
ai
Different similarity criteria can been used, for ex-
ample “Pearson’s Correlation” is a frequent alterna-
tive to cosine similarity. This form of KNN is quite
primitive, and some authors proposed various im-
provements. However, as shown in the Netflix prize,
these improvements cannot overturn extremely neg-
ative results. Therefore, we decided to implement
these two basic versions of the KNN to have an idea
of its initial performance. In the following KNN 1 is
based on Cosine Similarity and KNN 2 on Pearson’s
Correlation.
2.2 Slope One
The Slope One algorithm compares similar items
rather than similar users and determines the “popu-
larity differential” between them. Essentially, it cal-
culates the difference δ between the average rating of
two items, j
1
and j
2
, and then uses this value to pre-
dict the rating for j
2
of a given user u
i
in the following
way:
prediction(u
i
,j
2
) = r
i
1
+ δ
If we look at this process in terms of linear
regression we can say that, instead of applying a
transformation like f(x) = ax + b it uses a reduced
form f(x) = x + b. When we have more than one
known r
i
we can get several predictions and so the
proposed best one is the average of all:
prediction =
∑
i
r
i
1
+δ
|R
i
|
where R
i
is the set of all relevant items. It has
been shown in (Lemire and Maclachlan, 2005) that
this algorithm can provide a good accuracy.
2.3 TMW
The idea underlying TMW is to form and maintain
an heterogeneous graph whose nodes are users and
places. This idea has been proposed by (Aggarwal
et al., 1999), and in (Huang et al., 2004) the au-
thors propose using a “two-layer graph” (one layer
for users and one for items). This approach is not
mainstream in the recommender system community
so we describe briefly the basic ideas of our TMW al-
gorithm below (details can be found in our previous
work (Roda et al., 2009)).
2.3.1 Formalization
Let U (for users) and P (for places) be two finite sets
and V = U ∪P the resulting vertex set. We introduce
the following two graphs:
• R = (V, A) is a bipartite digraph; A ⊆ U ×P is
weighted by a function ρ : A → [−1, 1] (weights
represent ratings).
• S = (U, B) is a graph weighted by a function γ :
B →[0, 1] (it represents the known social network
and weights represent the “trust” between users).
G = R ∪S is the union of the two graphs which
models a mixed network (ratings and social relation-
ships). It is a base to infer new relations and to mod-
ify existing ones exploiting the fact that sometimes
users like (almost) the same places in (almost) the
same way. While the system gets more information
(i.e. new ratings are expressed by old and new users)
new relations can be established and the social net-
work grows (formally, G evolves in a richer graph G
′
).
In order to produce a prediction for a given user and a
given place, we have to find the best “stream of infor-
mation” in this augmented and dynamic network.
WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies
604
2.3.2 Identification of Maximum Confidence
Paths
We treat this problem as an optimization problem and
try to consider this situation as a stream of informa-
tion which flows in the social network, constrained by
the level of trust users share each other. Intuitively, we
look for the best path between the active user and the
best mentor. We make the assumption that the confi-
dence for a path is defined by the lowest confidence
arc in the path, thus trusting the “word of mouth” if
this flows through trusted users only, and we discard
a path if it contains an “unreliable” agent.
The problem reduces to finding the maximum con-
fidence path between a user and the best mentor: this
is the same as finding a path whose arc of minimum
weight is maximum between all the path minima,
which is precisely the so-called maximum capacity
path problem. Algorithms are known to solve this
problem in time linear in the number of arcs (Punnen,
1991). When the best path is found we take the last
but one edge m
best
as the best mentor and the weight
of the very last arc (i.e., its rating) as the prediction.
In parallel, we carry out the computation of the
value of the bottleneck which represents a trust level
and which allows us to choose trusted recommen-
dations. When the trust level is lower than a cer-
tain threshold, we replace the TMW prediction with
a value computed as the linear regression between
user’s ratings and the average community rating.
3 EVALUATION OF THE
ALGORITHMS
We use a simple metric to evaluate our system, in
order to have clear results easy to communicate to
non technical stakeholders. The choice was made be-
cause of the clamour of the Netflix competition and
so we used the same metric: accuracy computed as
the square root of the averaged squared difference be-
tween each prediction and the actual rating (the root
mean squared error or “RMSE”). Let the r
ui
denote
the actual rating provided by a certain user u for an
item i, with i= 1, 2, ..., n
u
(n
u
≤n, where n is the num-
ber of all available items) and let p
ui
denote the pre-
diction generated by a certain algorithm for the same
user and the same item. RMSE, relating to user u, is
defined by:
RMSE
u
=
s
∑
n
u
u=1
(r
ui
− p
ui
)
2
n
u
The total RMSE is obteined as the average of the
RMSE of all users. As mentioned above, the evalua-
tion of RMSE is typically performed using the “leave-
n-out” approach , where a part of the dataset is hidden
and the the rest is used as a training set for the rec-
ommender, which tries to predict properly the with-
held ratings. Here we employ a different method, due
to the possibility of recording ratings and predictions
live. TMW is currently used as the main recommen-
dation algorithm for a website to which we have au-
thorized access; in this way we don’t need to simulate
the prediction process because we can compare pre-
dictions with real ratings from users. Using the web-
site users enter ratings for places (such as restaurant,
bars, etc.), on a scale from 0 to 5, and can receive
recommendation based on their voting history.
For our experiment we proceed as follows: every
time a user provides a rating, we calculate the pre-
dictions with all the three algorithms described above
using the entire dataset (with the exception of the rat-
ing entered), and store all the prediction results. Ba-
sically, for every rating R(u
i
, p
k
), we record a line in
a log file with the predictions about that item and user
of TMW, KNN 1 (using cosine similarity), KNN 2
(using Pearson correlation) and Slope One, respec-
tively, as shown in Table 1.
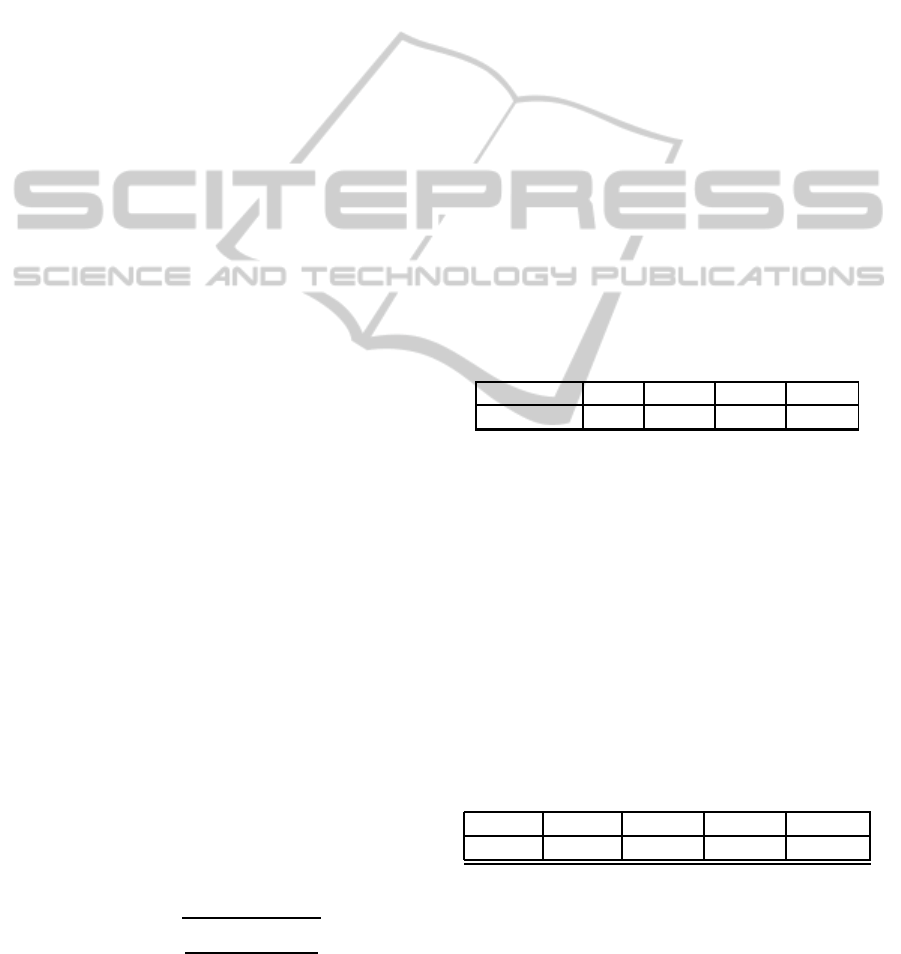
Table 1: Log line for the experiment.
rating (real) TMW KNN 1 KNN 2 Slope 1
R(u
i
, p
k
) Pr
tmw
Pr
knn
1
Pr
knn
2
Pr
sl1
As a benchmark to evaluate all the algorithms we
employ the community average for a certain item,
with the aim of measuring how much each algorithm
can improve the simple community recommendation.
Thus, we also compute the RMSE of the commu-
nity recommendationwith respect to the actual ratings
provided by users.
The results reported in the following tables refer
to the analysis we performed using the ratings we got
over the first four months of activity of the website.
We have 315,463 ratings, inserted by 69,794 users on
147,319 items (places). Table 2 reports the overall
RMSE computed in this period.
Table 2: RMSE for all ratings.
comm. TMW KNN 1 KNN 2 Slope 1
1.0710 0.9865 0.9872 0.9884 0.9859
In Table 3 we express this result in relative terms
by providing the rate of improvement with respect to
the average of the ratings by the community: for in-
stance, TMW improves community ratings by 7.89%
on average.
EVALUATION OF COLLABORATIVE FILTERING ALGORITHMS USING A SMALL DATASET
605

Table 3: Improvement over community average.
Algorithm Improvement over community avg.
TMW 7.89 %
KNN 1 7,82 %
KNN 2 7,71 %
Slope One 7,95 %
4 DISCUSSION AND
CONCLUSIONS
A first consideration is that all the algorithms don’t
supply predictions dramatically more accurate than
the community average. Even if it is well known now
(see Netflix prize results) that an improvement of a
few percentage points of accuracy is hard to get, still
in absolute terms the RMSE seems a bit excessive (re-
member that votes range from 0 to 5). Indeed, in all
cases the RMSE is always greater than 0.9, represent-
ing an average error in the order of 20% on the actual
ratings.
A second observation is that our results do not
clearly show which algorithm works better. TMW
provides slightly better results than KNN but their
outcomes are very similar. We find a bit surprising
that KNN using cosine similarity performs better than
the one based on Pearson Correlation and that Slope
One performs better than both of them. Indeed, in
line with previous works we expected KNN based on
Pearson Correlation to perform the best. We iden-
tify two possible reasons. First, we considered a plain
version of KNN and did not investigate possible im-
provements. Second, TMW only looks for the best
mentor available, instead of carrying out a full neigh-
bourhood formation, which could pose problems in a
sparse dataset.
We suspect that the results obtained in our exper-
iments are due to the structure and the dimension of
the dataset. Indeed, the training data set of Netflix
consists of 100 million ratings provided by over 480
thousand users, on nearly 18 thousand movie titles.
Group Lens provides three datasets, one of 100,000
ratings by 943 users for 1,682 movies, another of 1
million ratings by 6,040 users for 3,900 movies, and a
third of 10 million ratings and 100,000 tags by 71,567
users for 10,681 movies. Jester Joke dataset has 4.1
million by 73,496 users on 100 jokes. On the contrary,
our dataset is sparser, and thus most of the RMSE
analyses that can be found in the literature do not ap-
ply to our case.
The main issue, which arises from our experience,
is that it is not clear which is the minimal dimension
of a dataset to make it a reliable base to build a test
bed. This a very important question in our opinion
and our impression is that it has been underestimated
in the literature. Of course, if a dataset is untrustwor-
thy an alternative consists in using public datasets, but
this may be audacious, because it may be not ideal
to tune a system to recommend places on a dataset
which was originated from a system to recommend
movies. Additionally, even if the collaborative filter-
ing approach works with generic items, new difficul-
ties may occur later when the system is extended with
content based capabilities.
In conclusion, this experiment has shown that
from the practitioner’s point of view, finding the best
algorithm is equivalent to finding a reliable dataset
and test bed, and that this issue has not been addressed
adequately in the literature.
REFERENCES
Aggarwal, C., Wolf, J., Wu, K.-L., and Yu, P. (1999). Hort-
ing hatches an egg: a new graph-theoretic approach
to collaborative filtering. In Fayyad, U., Chaudhuri,
S., and Madigan, D., editors, Proceedings of the fifth
ACM SIGKDD international conference on Knowl-
edge discovery and data mining, pages 201–212, New
York. ACM.
Breese, J., Heckerman, D., and Kadie, C. (1998). Empirical
analysis of predictive algorithms for collaborative fil-
tering. Technical Report MSR-TR-98-12, Microsoft
Research.
Huang, Z., Chung, W., and Chen, H. (2004). A graph model
for e-commerce recommender systems. Journal of the
American Society for Information Science and Tech-
nology, 55(3):259–274.
Lemire, D. and Maclachlan, A. (2005). Slope one predic-
tors for online rating-based collaborative filtering. In
Proceedings of SIAM Data Mining (SDM’05).
Punnen, A. (1991). A linear time algorithm for the max-
imum capacity path problem. European Journal of
Operational Research, 53:402–404.
Roda, F., Liberti, L., and Raimondi, F. (2009). Com-
binatorial optimization based recommender systems.
In Proceedings of the 8th Cologne-Twente workshop
(CTW09) on Graphs and Combinatorial Optimiza-
tion, Paris.
Vozalis, E. and Margaritis, K. (2003). Analysis of rec-
ommender systems algorithms. In Lipitakis, E., ed-
itor, The 6th Hellenic European Conference on Com-
puter Mathematics & its Applications, pages 732–745,
Athens. Athens University of Economics and Busi-
ness.
WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies
606
