A GRAPH DECOMPOSITION APPROACH

TO WEB SERVICE MATCHMAKING

S. Lagraa, H. Seba, R. Khennoufa and H. Kheddouci

Lab. GAMA, Université Claude Bernard Lyon1, Université de Lyon, IUT Lyon1, Villeurbanne Cedex, France

Keywords:

Web services, Semantic web services, OWL-S, Graph matching, Graph decomposition, Graph edit distance,

Graph kernel.

Abstract:

Web service discovery is becoming a critical issue in several ﬁelds. The current approaches for service dis-

covery and mainly semantic web services such as OWL-S are limited primarily to the matching of their in-

puts/outputs at the level of an ontology. Recent studies show that this approach does not sufﬁce to discover

web services and that the structure of web services has an important and necessary weight in the efﬁciency

of the matching. The structure of a web service can be represented by a graph. The problem of matching

semantic web services is then translated into a problem of graph matching. In this work, we propose a match-

ing approach that ﬁrst decomposes the web service graph into more simple sub-structures then, the matching

process is achieved onto these substructures. The proposed algorithms achieve better time complexity than

existing ones. We also propose a semantic similarity to enhance our structural similarity.

1 INTRODUCTION

With the rapid development of e-commerce over In-

ternet, web services are becoming an essential tech-

nology for several enterprises. With the web service

technology, an enterprise publishes its activities and

services on the web and consequently has access to

more clients. The challenge is then how to simplify

service discovery to the potential clients? So, web

service discovery is becoming a critical research area.

The task of web service discovery implies comparing

web service descriptions and select the one that corre-

sponds to the demand. To address this problem many

simple search engines that provide keyword search on

web service descriptions have been proposed. This

approach is insufﬁcient mainly because keywords do

not capture the underlying semantics of web services

and do no sufﬁce for accurately specifying users’ in-

formation needs (Dong et al., 2004). To deal with

these limitations, researchers follow two complemen-

tary directions:

1. Explore new matching methods that use other in-

formation about web service descriptions that can

assist the user when selecting among similar web

services.

2. Enhance the description of web services by

adding more information that may be useful to the

matchmaking process. In this context semantic

descriptions of web services are of high impor-

tance. So web service description languages such

as OWL-S (Web Ontology Language for Web Ser-

vices) receive much interests.

This paper focuses on addressing the problem of

web service matchmaking in the context of both ap-

proaches. The contribution of this work can be sum-

marized as follows:

1. We propose two algorithms for web service

matching. The key part of our algorithms is a

decomposition approach that simpliﬁes the com-

plexity of the matching process while using both

structural and semantic information in the match-

ing process.

2. Based on graph kernels to extract similar entities,

we propose a new semantic metric for the com-

parison of web services’ inputs/ouputs.

We have implemented a prototype and conducted sev-

eral experiments to evaluate the effectiveness and ef-

ﬁciency of our matching approach. Our results show

that our solution outperforms existing ones.

The rest of the paper is organized as follows: in Sec-

tion 2, we begin with a discussion of the current state

of the art in web service matching. Following, in Sec-

tion 3, we ﬁrst present a general description of our

scheme and its theoretical foundations. Then, we pro-

Lagraa S., Seba H., Khennoufa R. and Kheddouci H..

A GRAPH DECOMPOSITION APPROACH TO WEB SERVICE MATCHMAKING.

DOI: 10.5220/0003338200310040

In Proceedings of the 7th International Conference on Web Information Systems and Technologies (WEBIST-2011), pages 31-40

ISBN: 978-989-8425-51-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

vide the details of our similarity measures. Finally,

we present the results of our experiments that evaluate

our approach and compares it with existing solutions.

Section 4 concludes this paper and presents our future

work.

2 RELATED WORK

Web service matching is an active research area

were several solutions are proposed. We fo-

cus here on semantic web service matchmaking

where concepts of semantic has been introduced

to overcome the limitations of the simple string

matching provided by UDDI (Universal Descrip-

tion Discovery and Integration http://uddi.xml.org/)

and WSDL (Web Services Description Language

http://www.w3.org/TR/wsdl). This has been achieved

by the means of description languages such as

OWL-S (Web Ontology Language for Web Services,

http://www.w3.org/Submission/OWL-S/). OWL-S

(formerly, DAML-S) provides three facets to describe

a web service: Service Proﬁle, Service Model and

Service Grounding that represent respectively De-

scription, Functionality and Access Mechanism of

web services (Bellur et al., 2008):

• Service Proﬁle: describes inputs, outputs, precon-

ditions and effects of the web service. Input and

output terms of the service are expressed as con-

cepts belonging to a set of ontologies. The use

of an ontology allows to refer to a single concept

from several syntactically different terms.

• Service Model: It describes a service as a process,

either atomic or composite. Composite processes

have a set of sub-processes associated with a con-

trol structure. The control structure will specify

the order in which different sub-processes are ex-

ecuted. Different types of control structures are:

Sequence, Split, Split+Join, Any-Order, Choice,

If-Then-Else, Iterate, Repeat While and Repeat

Until.

• Service Grounding: Grounding deals with the re-

alization of services. It provides concrete details

necessary to invoke the service such as message

format, transfer protocol, etc.

The earlier matching approaches of OWL-S web ser-

vices (Mandell and McIlraith, 2003) use only service

proﬁle in the matching process and mainly inputs and

outputs parameters. In (Bellur and Vadodaria, 2008),

Bellur et al. present a comprehensive review of cur-

rent approaches in semantic web service matchmak-

ing. One of the pioneers in this context is the work of

Paloucci et al. (Paolucci et al., 2002) that deﬁnes four

similarly degrees between concepts: Exact, Plug-in,

Subsume and Fail. Let AdOp be one of the concepts

of the outputs of an advertisement and QOp be one of

the concepts of the outputs of a query. Exact means

that QOp and AdOp are equivalent. Plug-in means

that QOp is a superclass of AdOp in the ontology, so

AdOp can be plugged in place of QOp. Subsumes

means that AdOp is a superclass of QOp, so the ad-

vertised service may fulﬁll the requirements of the re-

quest. Fail means that no relation is found between

the compared concepts.

In (Bellur and Kulkarni, 2007), the authors ex-

tends the algorithm of (Paolucci et al., 2002) by com-

puting a matching in a bipartite graph composed of

the concepts of the published services and those of

the query. In (Bellur et al., 2008), the authors con-

sider pre-condition matching in addition to inputs

and outputs. In (Guo and Chen, 2005), the authors

present a similarity measure that allows advertise-

ments and requests to be expressed in different on-

tologies. In (Beck and Freitag, 2006), the authors

present a method for semantic matchmaking which

takes into account the preference of concepts pro-

vided by the user. (Vu et al., 2006) consider the QoS

information through the matching process. For this,

the author suppose the existence of an interface where

users can submit their feedback on the perceived QoS

of consumed services. Wand and Stroulia (Wang and

Stroulia, 2003) were the ﬁrst researchers that intro-

duced the structure of web service operations dur-

ing web service discovery. Their matching method is

based on the hierarchical structure of the XML syn-

tax of WSDL speciﬁcations. For this, they adapted a

tree edit distance algorithm (Garofalakis and Kumar,

2003) to the matching of WSDL speciﬁcations. In

(Dong et al., 2004), Dong et al. built Woogle, a web

service search engine that uses a clustering algorithm

to group names of parameters of web-service oper-

ations into semantically meaningful concepts. Then

these concepts are used to measure similarity of web-

service operations. In (Shen and Su, 2005), Shen and

Su formally deﬁne a behavior model for web service

by automata and logic formalisms. In (Dijkman et al.,

2009), the authors use graphs to represent web ser-

vice operations. Then, they use graph matching al-

gorithms proposed in (Messmer and Bunke, 1999)

to compare graphs. However, these algorithms are

space search based and consequently have an expo-

nentiel time complexity. In (Corrales et al., 2008),

authors also use graphs to match semantic web ser-

vices. To match web service graphs, they use an A*

based algorithm proposed in (Messmer, 1995). A* is

an algorithm that uses a depth ﬁrst search approach to

traverse a tree representing all the possible matching

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies

situations of the compared graphs. Hao et al. (Hao

and Zhang, 2007) discover similar web services by

matching the XML trees corresponding to data types

in WSDL. In (Mbareck and Tata, 2006), authors use

Petri nets to represent and compare web service op-

erations. In (Nejati et al., 2007) and (Wombacher,

2006), authors use ﬁnite state machine to represent

web service operations.

3 A DECOMPOSITION

APPROACH TO WEB SERVICE

MATCHMAKING

3.1 Overview

To address the challenges involved in searching for

web services more information must be considered.

Among these information, the structure of web ser-

vice operations is perhaps the most important. With

OWL-S, this structure can be represented by a graph.

A graph of an OWL-S process is a labeled directed

graph G = (V

, E) where:

• V

is the set of vertices that represent the atomic

activities of the service.

• V

est the set of vertices that correspond to control

structures such as choice, sequence, if-then-else,

etc. These structures can be represented by logic

connectors namely XOR et AND. For instance, a

choice is represented by an XOR.

• E is the set of edges that bind the different ver-

tices.

Furthermore, a process graph can have a vertex "start"

and one or several vertices "end" (Mendling et al.,

2006). Figure 1 gives un example of an OWL-S pro-

cess and its corresponding graph.

In the case of non cyclic operations, an OWL-S

process can also be represented by a tree where the

root and the internal nodes are the different control

structures (choice, sequence, if-then-else,..., etc.)

and the leafs are the atomic services.

When web service operations are represented by

graphs, the problem of their matching is a problem of

comparing the corresponding graphs. The problem of

graph comparison received a lot of interest (Bunke,

2000). The main traditional algorithmic approaches

to graph comparison are graph isomorphism and inex-

act matching (Borgwardt and Kriegel, 2005). Graph

isomorphism checks for topological identity. Inex-

act matching or error-tolerant matching does not en-

force strict matching of graphs. Inexact matching al-

gorithms generally computes a distance between the

compared graphs. This distance measures how much

these graphs are similar and is associated to a cost

function. Graph edit distance is the most used inex-

act matching measure. Similarity or edit distance be-

tween two graphs is the minimum number of edit op-

erations needed to transform one graph into the other

(Bunke and Allermann, 1983; Sanfeliu and Fu, 1983).

An edit operation is an insertion, a suppression or a re-

labeling of a vertex or an edge in a graph. To each edit

operation e

is associated a cost c(e

) and the edit dis-

tance between two graphs G

and G

is then the min-

imum cost related to the set of operations that trans-

form G

into G

d(G

, G

) = min

,...,e

)∈ϒ(G

)

∑

i=1

c(e

) (1)

where ϒ(G

, G

) is the set of edit operations that

transform G

into G

. However, ﬁnding the minimal

edit distance is NP-hard (Bunke, 1999) and it is of-

ten difﬁcult to ﬁnd the appropriate costs for individual

edit operations (Borgwardt and Kriegel, 2005). So,

searching for other graph matching approaches is still

an open question. Graph kernels is one of the most re-

cent approaches to graph comparison that is presented

as an alternative to existing solutions. Graph kernels

have the particularity of integrating concepts from all

former approaches to graph comparison. Graph ker-

nels belong to a class of kernels on structured data

called R-convolution kernels or decomposition ker-

nels (Haussler, 1999). Roughly speaking, the idea

of graph kernels is constructing similarity of graphs

based on the similarity of small parts, i.e. sub-graphs,

of the compared graphs. The concept of decomposing

a discrete compound object x into parts (x

, x

, ..., x

)

can be formally modeled by a predicate R that re-

turns true if (x

, . . . , x

) is a valid decomposition of

x. The set of all valid decompositions of x is noted

−1

(x) = {(x

, . . . , x

) : R(x

, . . . , x

)}. The kernel

function k between two objects x and x

′

is given by

(Haussler, 1999):

k(x, x

′

) =

∑

,...,x

)∈R

−1

(x)

′

,...,x

′

)∈R

−1

′

)

∏

i=1

, x

′

) (2)

where k

is a kernel that gives the similarity be-

tween two parts.

For graphs, the natural and most general R-

convolution kernel would decompose each of the two

compared graphs G and G

′

into all of their subgraphs

and compare them pairwise. This all-subgraphs ker-

nel is deﬁned as follows (Borgwardt and Kriegel,

2005):

k(G, G

′

) =

∑

S⊆G

′

⊆G

′

(S, S

′

) (3)

A GRAPH DECOMPOSITION APPROACH TO WEB SERVICE MATCHMAKING

</Choice>

</sequence>

</Choice>

Start

XOR

GetCoordinatesBy

CityAndState

GetDistanceBetween

TwoCoordinates

XOR

GetAddress

GetStateAnd

Province

GetZone

End

Coordinates

Figure 1: A graph representation of an OWL-S process.

In (Gartner et al., 2003) the authors show that

the problem of computing this all-subgraphs kernel

is NP-hard. So, several other alternatives have been

deﬁned in the literature. These alternatives focus on

proposing simpler decompositions such as sequences

of vertices (Neuhaus and Bunke, 2006), paths (Suard

and Rakotomamonjy, 2007), shortest paths (Borg-

wardt and Kriegel, 2005), trees (Ramon and Gart-

ner, 2003),etc. The idea of decomposing the graphs

to be matched prior to the matching process has also

been used with graph edit distance and the results are

promising. In (Jouili and Tabbone, 2009; Riesen and

Bunke, 2009) the authors use a star decomposition of

the graphs and then deﬁne graph edit distance onto

the obtained sub-structures.

3.2 Our Approach

It follows from the above description of graph match-

ing approaches that graph decomposition allows to

have more efﬁcient solutions either via graph kernels

or graph edit distance. The question here is what is the

decomposition to use when matching web services?

To attempt to give a satisfactory answer, we pro-

pose here two kinds of decomposition of web service

graphs through two matching algorithms: Algorithm

1 and Algorithm 2. Both of them focus on the main

characteristic of the graphs of web service business

processes: directed edges. Algorithm 1 uses graph

kernels and Algorithm 2 uses graph edit distance. We

also attempt to reduce the matching delay by avoiding

redundancy in the obtained sub-structures.

3.3 Algorithm 1

In this algorithm, we extend an existing graph decom-

position, the star decomposition, to take into account

edge-direction. We call this star, where all edges are

out-coming edges, a FaS for Father and Sons sub-

structure. A FaS substructure is composed of a node

connected to its sons by out-coming edges. This de-

composition is adapted for web services which graphs

do not contain cycles. So we apply it for trees of web

service operations. Figure 2 shows an example of a

decomposition of an OWL-S process tree into FaS

substructures.

Figure 2: Decomposition of a service tree into FaSs.

3.3.1 Principle

To compare two OWL-S processes, we ﬁrst decom-

pose their corresponding trees into FaSs. Then, each

FaS of the ﬁrst process is compared to every FaS of

the second process (see Algorithm 1). Comparing a

pair of FaSs FaS

and FaS

consists to compute the

kernel function

k(FaS

, FaS

) = exp

−d(FaS

,FaS

)

(4)

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies

which allows us to ﬁnd for a given FaS

of the ﬁrst

tree the most similar FaS

of the second tree given by

the best value of k(FaS

, FaS

) noted Sim(i, j). Then,

we compute the kernel of the two compared trees by

summing all these best values :

K(A

, A

) =

,nA

∑

i=1, j=1

Sim(i, j) (5)

Algorithm 1 : Matching algorithm using a decomposi-

tion into FaSs and tree kernels.

Input:Two OWL-S process trees A

and A

Output: similarity degree between A

and A

computed as

a tree kernel

Begin

Decompose A

and A

into FaSs.

For i = 1, nA

do For j = 1, nA

do Sim(i, j) = 0; EndFor

EndFor;

For i = 1, nA

do // nA

is the number of FaSs in A

For j = 1, nA

// nA

is the is the number of FaSs in A

do /* compare FaS

and FaS

father

(FaS

, FaS

) =

(

0 if f ather

FaS

= father

FaS

1 otherwise

son

(FaS

, FaS

)) =

max(kFaS



FaS



) −



FaS

∩ FaS



edge

(FaS

, FaS

) = |kedge(FaS

)k −



edge(FaS

)



d(FaS

, FaS

) = d

father

(FaS

, FaS

) + d

son

(FaS

, FaS

)) +

edge

(FaS

, FaS

) k(FaS

, FaS

) = exp

−d(FaS

,FaS

)

If k(FaS

, FaS

) > Sim(i, j) Then

Sim(i, j) = k(FaS

, FaS

); EndIF

EndFor EndFor

K(A

, A

) =

,nA

∑

i=1, j=1

Sim(i, j) //tree kernel of A

and A

END

3.3.2 Example

Figure 3 illustrates a matching example of two web

service trees A

and A

with Algorithm 1. The de-

composition gives 2 FaS substructures for each tree.

The best value of the kernel function for FaS

)

is the one that matches it with FaS

) and it is

equal to e

−2

. The best value of the kernel function

for FaS

) is the one that matches it with FaS

)

and it is also equal to e

−2

. So, the ﬁnal value of the

similarity between the two trees is e

−2

+ e

−2

= 2e

−2

3.3.3 Time Complexity

The algorithm has a complexity of O(△n

) time steps

where n is the number of vertices in the largest tree

and △ is the maximum degree in the tree. In fact

the complexity of the decomposition into FaS sub-

structures is polynomial. In the worst case it is

O(△n). To match the obtained sets of FaSs, we need

O(△n

) time steps. This gives a global complexity of

O(△n

+△n = △n

) time steps. As in the worst case

△ = n, we have a complexity of O(n

3.4 Algorithm 2

In this algorithm, we propose a new graph decom-

position that emphasizes edges and their direction.

This decomposition, called EaS for (Edge and its end-

point Stars) is a graph sub-structure composed of a

directed edge, its endpoint vertices and all the out-

coming edges from the two endpoints. Figure 4 shows

an example of decomposition of a graph into EaSs.

3.4.1 Principle

To compare two OWL-S processes, we ﬁrst decom-

pose their corresponding graphs into EaSs. Then

each EaS of the ﬁrst process is compared to every

EaS of the second process (see Algorithm 2). Com-

paring a pair of EaSs: EaS

and EaS

consists to

compute the edit distance between two sub-graphs

Sim(i, j) = d(EaS

, EaS

). Sim is a nG

× nG

ma-

trix, where nG

(resp. nG

) is the number of EaSs in

(resp. G

), that saves the computed distances (see

Figure 5). Then, the distance between the two graphs

is the sum of the minimal distances between EaSs.

Algorithm 2 : Matching algorithm based on EaS. and

Edit distance.

Input: Two OWL-S process graphs G

and G

Output: similarity degree between G

and G

computed as

a graph edit distance

Begin

Decompose G

and G

into EaSs.

For i = 1, nG

do For j = 1, nG

do Sim(i, j) = 0; EndFor

EndFor;

For i = 1, nG

For j = 1, nG

do /* compare EaS

and EaS

d(EaS

, EaS

) = c( f ather

, father

) + c(son

, son

) +

|kE(EaS

)k −



E(EaS



where c(x, y) is the cost of the substituting x by y.

Sim(i, j) = d(EaS

, EaS

)

EndFor

d(G

, G

) =

,NG

∑

i=1, j=1

min Sim(i, j)

|nG

−nG

+ |kG

k − kG

where nG

(resp. nG

) is the number of EaSs in G

(resp.

)

End

A GRAPH DECOMPOSITION APPROACH TO WEB SERVICE MATCHMAKING

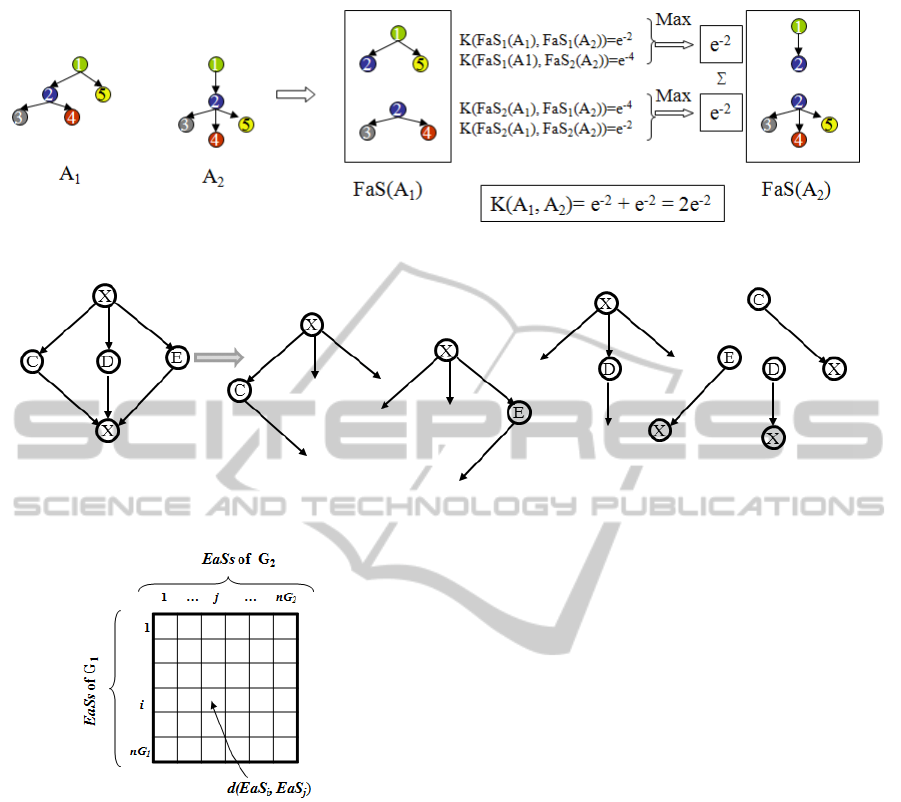
Figure 3: A matching example with Algorithm 1.

Figure 4: Example of decomposing a graph into EaSs.

Figure 5: Similarity matrix between EaSs.

3.4.2 Example

Figure 6 illustrates a matching example of two graphs

and G

with Algorithm 2. The decomposition

gives 5 EaS substructures for G

and 3 EaS substruc-

tures for G

. The matrix of similarity Sim between

EaSs is 5 × 3. In Figure 6, each EaS is represented

by the directed edge that determines it i.e. a pair

of nodes ( f ather, son). Each cell of the matrix con-

tains the edit distance between two EaSs. For exam-

ple Sim(1, 1) = 2 because if we consider that all edit

operations have the same cost 1, then the distance be-

tween EaS

) and EaS

) is equal to the cost of

two re-labelling operations: 2 to 1 and 3 to 2. By sum-

ming the minimal distance between all pairs of EaSs,

we obtain a distance between the two graphs equal to

3.4.3 Complexity

The complexity of Algorithm 2 is O(n

) where n is

the number of vertices in the largest graph. In fact,

to decompose a graph of n nodes into EaSs we need

O(n

) time steps. To compare two EaSs, we need

2△

time steps where △ is the maximum degree in

the graph. So, if we consider that, in the worst case

a graph of n nodes has 2n EaSs then to construct the

matrix Sim of all comparisons between the EaSs, of

two graphs, we need O(4n

∗ 2△

) = O(n

△

) time

steps.

To compute the minimum distance between EaSs,

we need O((2n)

) = O(4n

) time steps.

So, the complexity of the algorithm is O(n

△

As in the worst case △ = n, we have a complexity of

O(n

3.5 Semantic Similarity

To obtain an accurate similarity measure, we also con-

sider semantic similarity of inputs and outputs. To do

so, we extended the semantic similarity of (Paolucci

et al., 2002) with Kernels. In fact, we propose a

kernel function to evaluate the four degrees of simi-

larity Exact, PlugIn, Subsume and Fail introduced in

(Paolucci et al., 2002). We affect a weight w to each

of the four degrees. This weight is either given by the

user or determined according to the application. So,

we compare two concepts cx

and cx

that correspond

to the inputs or outputs x

and x

of the compared ser-

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies

Figure 6: A matching example with Algorithm 2.

vices by the following function:

Sem

, x

) =











Exact

if Exact(cx

, cx

)

PlugIn

∗

d(cx

,cx

)

if PlugIn(cx

, cx

)

Subsumes

∗

d(cx

,cx

)

if Subsumes(cx

, cx

)

Fail

otherwise

(6)

where d(cx

, cx

) is the number of edges that separate

the two concepts cx

and cx

in the ontology.

Thus, our semantic similarity of two services S

and S

measures the sum of the most similar inputs

and outputs of the two services as follows:

k(S

, S

) =

nbS

,nbS

∑

∈S

max k

Sem

, x

) (7)

where nbS

(resp. nbS

) is the number of in-

puts/outputs of S

(resp. S

) and k

Sem

, x

) is the

similarity between two concepts.

3.5.1 Example

Let S be a published service with two input param-

eters: "vehicle" and "parts" and one output "price".

Let Q a query with input parameters "Car" and "parts"

and one output "price". We suppose that the ontology

is the one presented on Figure 7 and that w

Exact

= 1,

Plug− In

= 0.8, w

Subsumes

= 0.5, w

Fail

= 0.

The similarity between the inputs of the published

service and the query is :











Sem

(car, vehicle) = w

PlugIn

∗

= 0.8

Max

⇒ 0.8

Sem

(car, parts) = w

Fail

= 0

(8)











Sem

(parts, vehicle) = w

Fail

= 0

Max

⇒ 1

Sem

(parts, parts) = w

Exact

= 1

(9)

The similarity between the outputs of the two services

is:

Sem

(price, price) = w

Exact

= 1

Max

⇒ 1 (10)

This gives the following similarity between the two

services:

k(S

, S

) = 0.8 + 1 + 1 = 2.8 (11)

Thing

Vehicle

Car

Bus

Sedan

coupe

Jeep

Thing

Vehicle

Car

Bus

Sedan

coupe

Jeep

Figure 7: Vehicle ontology.

3.6 Evaluation

We implemented our matching scheme to evaluate its

performance and compare it with the performance of

exiting matching approaches of web services. In this

section, we provide an overview of our experiments

and some of the results we obtained. The experiments

were conducted on a Windows XP Laptop with a 1.73

GHz Pentium IV CPU and 1Gb main memory. The

data set used in our tests is a web service repository

A GRAPH DECOMPOSITION APPROACH TO WEB SERVICE MATCHMAKING

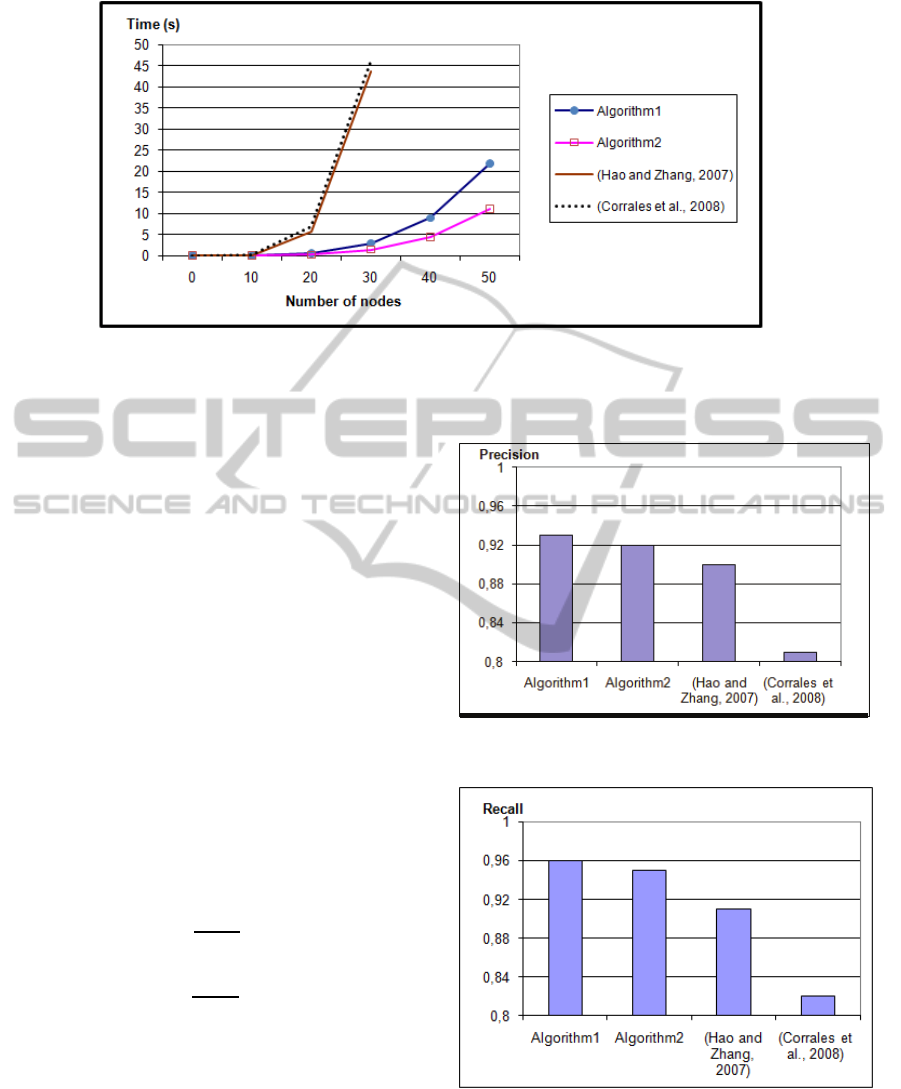
Figure 8: Execution time vs. the size of the graph.

collected by (Gater et al., 2010). We evaluated our

scheme by comparing it with two other methods that

embed structure matching within web service match-

making: (Corrales et al., 2008) and (Hao and Zhang,

2007) described in Section 2.

We ﬁrst evaluated the execution time performance

of the four algorithms. The time performanceis tested

with the increase of the number of nodes of the com-

pared graphs. Figure 8 shows the variation of exe-

cution times according to the size of target graphs.

The results reported in this graphic represent the aver-

age execution times found for each given target graph

size. It can be seen that the execution times of Algo-

rithm 1 and Algorithm 2 are less than those of (Cor-

rales et al., 2008) and (Hao and Zhang, 2007). The ex-

ecution time is polynomial w.r.t the number of nodes

in the target graph. Moreover, the slope of Algorithm

1 id higher than for Algorithm 2.

We then evaluated the effectiveness of our ap-

proach by computing the recall and precision ratios

(Dong et al., 2004). The precision p and recall r are

deﬁned as follows:

p =

A+ B

(12)

r =

A+C

(13)

where A stands for the number of returned relevant

services, B stands for the number of returned irrel-

evant services, C stands for the number of missing

relevant services, A + C stands for the total number

of relevant services, and A + B stands for the total

number of returned services. As shown in Figure 9,

the precisions of our schemes is 93% for Algorithm 1

and 92% for Algorithm 2 outperforming the two other

methods. As it can be seen in Figure 10, the recall of

our schemes is 96% for Algorithm 1 and 95% for Al-

gorithm 2 also outperforming the two other methods.

Figure 9: Precision.

Figure 10: Recall.

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies

4 CONCLUSIONS

In this paper, we presented two decomposition-based

web service matchmaking methods. The main ad-

vantage of decomposing the web service graph into

smaller sub-structures is to reduce the time complex-

ity of the matching. The proposed algorithms take

into account the main characteristic of web service

graphs: directed edges and use the most efﬁcient

graph matching tools: graph kernels and graph edit

distance. We also augmented our structural match-

ing by a semantic similarity measure that enhance the

matching precision. Experimental results show that

the proposed algorithms are efﬁcient and outperform

existing ones. An interesting future extension con-

sists in using this approach with large web service

databases.

ACKNOWLEDGEMENTS

This work was funded by the ANR AOC and the CCI

de l’Ain.

REFERENCES

Beck, M. and Freitag, B. (2006). Semantic matchmaking

using ranked instance retrieval. In SMR ’06: 1st In-

ternational Workshop on Semantic Matchmaking and

Resource Retrieval, Co-located with VLDB.

Bellur, U. and Kulkarni, R. (2007). Improved matchmaking

algorithm for semantic web services based on bipar-

tite graph matching. In ICWS’07, IEEE International

Conference on Web Services.

Bellur, U. and Vadodaria, H. (2008). On extending seman-

tic matchmaking to include precondition and effect

matching. In International Conference on Web Ser-

vices, 2008, Beijing, China.

Bellur, U., Vadodaria, H., and Gupta, A. (2008). Seman-

tic Matchmaking Algorithms, chapter Greedy Algo-

rithms. Witold Bednorz, InTech, Croatia.

Borgwardt, K. and Kriegel, H.-P. (2005). Shortest-path ker-

nels on graphs. In 5th Int. Conference on Data Mining,

page 74–81.

Bunke, H. (1999). Error correcting graph matching: On the

inﬂuence of the underlying cost function. IEEE Trans.

Pattern Anal. Mach. Intell., 21(9):917–922.

Bunke, H. (2000). Recent developments in graph matching.

In ICPR, pages 2117–2124.

Bunke, H. and Allermann, G. (1983). Inexact graph match-

ing for structural pattern recognition. Pattern Recog-

nition Letters, 1:245–253.

Corrales, J. C., Grigori, D., and Bouzeghoub, M. (2008).

Behavioral matchmaking for service retrieval: Ap-

plication to conversation protocols. Inf. Syst., 33(7-

8):681–698.

Dijkman, R., Dumas, M., and Garcia-Banuelos, L. (2009).

Business Process Management, LNCS 570, page

48–63. Springer.

Dong, X., Halevy, A., Madhavan, J., Nemes, E., and Zhang,

J. (2004). Simlarity search for web services. In

VLDB2004, pages 372–383.

Garofalakis, M. and Kumar, A. (2003). Correlating xml

data streams using tree-edit distance embeddings. In

ACM PODS’2003. San Diego, California, June 2003,

pages 143–154. ACM Press.

Gartner, T., Flach, P., and Wrobel, S. (2003). On graph

kernels: Hardness results and efﬁcient alternatives. In

Springer, editor, Annual Conf. Computational Learn-

ing Theory, page 129–143.

Gater, A., Grigori, D., and Bouzeghoub, M. (2010). Owl-

s process model matchmaking. In IEEE Interna-

tional Conference on Web Services, July 5-10, Miami,

Florida, USA.

Guo, J. L. R. and Chen, D. (2005). Matching semantic web

services across heterogenous ontologies. In CIT 05,

the Fifth international conference on computer and in-

formation technology.

Hao, Y. and Zhang, Y. (2007). Web services discovery based

on schema matching. In the thirtieth Australasian con-

ference on Computer science - Volume 62.

Haussler, D. (1999). Convolution kernels on discrete struc-

tures. Technical Report UCSC-CRL-99-10, Univer-

sity of California, Santa Cruz.

Jouili, S. and Tabbone, S. (2009). Attributed graph match-

ing using local descriptions. In ACIVS 2009, LNCS

5807, page 89–99.

Mandell, D. and McIlraith, S. (2003). A bottom-up ap-

proach to automating web service discovery, cus-

tomization, and semantic translation. In Proceedings

of the Twelfth International World Wide Web Confer-

ence Workshop on E-Services and the Semantic Web

(ESSW),Budapest.

Mbareck, N. O. A. and Tata, S. (2006). Bpel behavioral

abstraction and matching. Business Process Manage-

ment Workshops, pages 495–506.

Mendling, J., Lassen, K., and Zdun, U. (2006). Transfor-

mation strategies between block-oriented and graph-

oriented process modelling languages. F. Lehner,

H. Nsekabel, P. Kleinschmidt, eds. Multikonferenz

Wirtschaftsinformatik, pages 297–312.

Messmer, B. (1995). Efﬁcient Graph Matching Algorithms

for Preprocessed Model Graphs. PhD thesis, Univer-

sity of Bern, Switzerland.

Messmer, B. T. and Bunke, H. (1999). A decision tree ap-

proach to graph and subgraph isomorphism detection.

Pattern Recognition, 32:1979–1998.

Nejati, S., Sabetzadeh, M., Chechik, M., Easterbrook, S.,

and Zave, P. (2007). Matching and merging of state-

charts speciﬁcations. In ICSE 2007, page 54–63.

A GRAPH DECOMPOSITION APPROACH TO WEB SERVICE MATCHMAKING

Neuhaus, M. and Bunke, H. (2006). A convolution edit ker-

nel for errortolerant graph matching. In IEEE interna-

tional conference on pattern recognition, Hong Kong,

page 220–223.

Paolucci, T., Kawmura, T., and Sycara, K. (2002). Semantic

matching of web service capabilities. In Springer Ver-

lag, LNCS, Proceedings of the International Semantic

Web Conference.

Ramon, J. and Gartner, T. (2003). Expressivity versus efﬁ-

ciency of graph kernels. In First International Work-

shop on Mining Graphs, Trees and Sequences.

Riesen, K. and Bunke, H. (2009). Approximate graph

edit distance computation by means of bipartite graph

matching. Image and Vision Computing, 27:950–959.

Sanfeliu, A. and Fu, K. (1983). A distance measure be-

tween attributed relational graphs for pattern recogni-

tion. IEEE Transactions on Systems, Man, and Cyber-

netics (Part B), 13(3):353–363.

Shen, Z. and Su, J. (2005). Web service discovery based on

behavior signatures. SCC, 1:279–286.

Suard, F. and Rakotomamonjy, A. (2007). Mesure de sim-

ilarité de graphes par noyau de sacs de chemins. In

21e colloque GRETSI sur le traitement du signal et

des images, Troyes.

Vu, F. P. L.-H., Hauswirth, M., and Aberer, K. (2006). A

search engine for qosenabled discovery of semantic

web services. International Journal of Business Pro-

cess Integration and Management, 1(4):244–255.

Wang, Y. and Stroulia, E. (2003). Flexible interface match-

ing for web-service discovery. In WISE’2003.

Wombacher, A. (2006). Evaluation of technical mea-

sures for workﬂow similarity based on a pilot study.

Meersman, R., Tari, Z. (eds.) OTM 2006. LNCS,

4275:255–272.

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies