
EMPLOYING MULTI-CORE PROCESSOR ARCHITECTURES
TO ACCELERATE JAVA CRYPTOGRAPHY EXTENSIONS
Mario Ivkovic and Thomas Zefferer
Secure Information Technology Center - Austria, Inffeldgasse 16a, Graz, Austria
Keywords:
Java, Cryptography, JCE, Parallelization.
Abstract:
For many years, the increase of clock frequencies has been the preferred approach to raise computational
power. Due to physical limitations and cost-effectiveness reasons, hardware vendors were forced to change
their strategy. Instead of increasing clock frequencies, processors are nowadays supplied with a growing
number of independent cores to increase the overall computational power. This major paradigm shift needs
to be considered in software design processes as well. Software needs to be parallelized to exploit the full
computing power provided by multi-core architectures.
Due to their intrinsic computational complexity, cryptographic algorithms require efficient implementations.
On multi-core architectures this comprises the need for parallelism and concurrent execution. To meet this
challenge, we have enhanced an existing Java
TM
based cryptographic library by parallelizing a subset of
its algorithms. Made measurements have shown speed-ups from 1.35 up to 1.78 resulting from the applied
modifications. In this paper we show that regardless of their complexity, several cryptographic algorithms
can be parallelized to a certain extent with reasonable effort. The applied parallelization of the Java
TM
based
cryptographic library has significantly enhanced its performance on multi-core architectures and has therefore
made a valuable contribution to its sustainability.
1 INTRODUCTION
Increasing the clock frequency of processors has been
the common approach of processor manufactures to
raise the performance of their products for many
years. This way, processors with operating clock
frequencies of up to several GHz have made their
way to the consumer market. A few years ago, this
evolution has finally taped off when chip manufac-
tures figured out that a further increase of clock fre-
quency is not cost-effectively achievable any longer
due to several physical limitations. In order to still
guarantee a continuous increase of computing power
for newly developed processors, vendors were forced
to modify their strategy. Instead of increasing the
maximum clock frequency, hardware manufacturers
have started to supply processors with multiple in-
dependent cores. Nowadays, modern processors are
equipped with four, eight, or even more cores, which
provide an increased computational power by pro-
cessing instructions in parallel.
This fundamental change of the design approach
had a significant impact on software development pro-
cesses too. On single-core architectures, the perfor-
mance of programs is directly correlated to the speed
of the processor, on which the software is running.
Increasing the clock frequency of the used processor
immediately leads to a speed-up of the particular soft-
ware too. Unfortunately, this is not true for multi-
core processor architectures. Although a processor’s
computing power is theoretically doubled when be-
ing equipped with a second core, most of the exist-
ing software has originally been developed to run on
single-core architectures. Hence, even though addi-
tional computing power is provided by supplementary
processor cores, it cannot be employed by software
that has originally been optimized to run on a single
core.
This problem has been described in an article by
Herb Sutter (Sutter, 2005). He concludes that soft-
ware that wants to make use of the full computing
power provided by multi-core processors needs to be
adapted accordingly. Only if the software assigns in-
dependent computations to different processor cores,
these computations can be executed concurrently and
the entire computing power provided by multi-core
processors can be employed. Unfortunately, writing
efficient and correct parallel programs and paralleliz-
5
Ivkovic M. and Zefferer T..
EMPLOYING MULTI-CORE PROCESSOR ARCHITECTURES TO ACCELERATE JAVA CRYPTOGRAPHY EXTENSIONS.
DOI: 10.5220/0003339000050012
In Proceedings of the 7th International Conference on Web Information Systems and Technologies (WEBIST-2011), pages 5-12
ISBN: 978-989-8425-51-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ing existing sequential programs are non-trivial tasks
that are still subject to ongoing research. Especially
the automatic parallelization of existing programs has
been the topic of numerous publications. Tools for the
automated parallelization of sequential source code
are for instance introduced in (Dig et al., 2009) and
(Bridges et al., 2008). Although some of the sug-
gested techniques appear to be promising, an ultimate
solution to this problem has not been found so far.
Parallelization of existing sequential programs is
especially important for software that performs com-
putationally intensive operations like scientific com-
putations and simulations. Another field of applica-
tion where complex computations have to be carried
out frequently is cryptography. Cryptographic algo-
rithms typically include some kind of secret key in
the processing of any given input data. The security
of cryptographic algorithms is usually proportional to
the size of the used key and relies on the fact that try-
ing out all possible key values is computationally in-
feasible within a reasonable period of time. As at-
tacks are becoming more effective - due to the in-
crease of available computational power and also be-
cause of parallelized and distributed approaches - key
sizes have to be increased too in order to preserve the
same level of security.
In general, cryptographic computations become
more time-consuming when key sizes are increased.
Therefore, it is crucial that existing cryptographic
libraries are adapted to utilize the entire comput-
ing power provided by modern multi-core proces-
sors. Only an appropriate parallelization of these li-
braries guarantees that they retain their level of per-
formance with increasing key sizes and remain usable
and future-proof.
Unfortunately, parallelization of cryptographic al-
gorithms is not a trivial task. For instance, consider
the design of the block cipher AES (Daemen and Rij-
men, 2002): a block of plain data is encrypted by ap-
plying the same set of operations for a specified num-
ber of times. The first iteration takes the plain data
as input, while subsequent rounds take the result of
the preceding round as input. Due to these data de-
pendencies between subsequent iterations, a parallel
execution of different rounds is infeasible.
Being aware of possible difficulties of paralleliz-
ing cryptographic algorithms, the goal of our work
was to evaluate whether existing cryptographic li-
braries can be optimized for a use on multi-core pro-
cessors. In this work we focused on the program-
ming language Java
TM
mainly because of two rea-
sons. First, a special API for the development of
concurrent programs (introduced by Doug Lea (Lea,
2005)) is available since version 1.5 of the Java
TM
De-
velopment Kit (JDK). The other reason is that we al-
ready had an existing Java
TM
cryptography library on
hand, which was perfectly suitable for our investiga-
tions.
To evaluate the possible performance boost of
cryptographic libraries on multi-core systems, we
have modified the existing Java
TM
cryptography li-
brary. Section 2 introduces this library in more de-
tail and shows how selected cryptographic algorithms
of the library have been improved to exploit the com-
puting power of multi-core architectures. In order to
compare the performance of the modified library with
the unmodified original version, we have conducted
several measurements on different architectures. The
results of these measurements and a summary of the
most important facts and findings are provided in Sec-
tion 3. Finally, Section 4 concludes this paper and
identifies further conceivable improvements to speed-
up cryptographic operations on multi-core processor
architectures.
2 JCE MODIFICATIONS
In this work we evaluate whether existing crypto-
graphic Java
TM
libraries can be improved in terms
of performance by applying parallelism. Therefore,
this section gives an short introduction to the Java
TM
Cryptography Extension (JCE) technology first. Fur-
thermore, this section provides a brief description of
different parallelization methods in Java
TM
and shows
how these methods have been applied to enhance
the performance of three selected cryptographic algo-
rithms.
2.1 Java Cryptography Extensions
Java
TM
Cryptography Extension (JCE) is a frame-
work for cryptographic operations like data encryp-
tion and decryption, key generation and key agree-
ment, message authentication codes (MAC), and
sealed objects. Regarding data encryption and de-
cryption, symmetric as well as asymmetric stream
and block ciphers are supported. Since version 1.4
of Java
TM
, the JCE is integrated into the SDK and no
longer an optional package.
The JCE uses a so-called provider architecture,
which guarantees implementation and, where possi-
ble, algorithm independence. Any signed provider
can be registered in the framework, which ensures that
the provided algorithms and implementations can be
used seamlessly. Furthermore, a provider from SUN
called SunJCE is supplied with the JDK per default.
For our investigations, we have analyzed the JCE
WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies
6

provider IAIK
1
and manually parallelized a subset of
its supported algorithms.
2.2 Parallelization in Java
Java
TM
has been providing built-in features for paral-
lelization from the very beginning. These low-level
APIs are very useful for simple parallelization tasks.
Since version 5.0 of the Java
TM
platform, a high-level
concurrency API is available for more advanced con-
currency tasks. Most of the functionalities are avail-
able in the java.util.concurrent packages. Data
structures for concurrent programming have also been
added to the collections framework.
We have implemented and compared two differ-
ent methods of parallelization in our work. The
first approach was the use of Executors from the
java.util.concurrent packages. Executors are
objects that encapsulate the creation and management
of threads from the executed tasks. ExecutorServices
are supplements to Executors and support Callable
objects that can return a value after parallel execution.
The following listing shows an example usage of the
Executors framework.
final ExecutorService ex =
Executors.newFixedThreadPool(2);
ParallelExp exp1 = new ParallelExp(...);
ParallelExp exp2 = new ParallelExp(...);
Future<?> future = ex.submit(exp1);
Future<?> future2 = ex.submit(exp2);
try {
future.get();
future2.get();
}catch (InterruptedException e) {
...
}
result1 = exp1.getResult();
result2 = exp2.getResult();
Functionalities provided in the java.util.concurrent
packages are mainly suitable for coarse-grained par-
allelization. For fine-grained parallelization a new
API, the ForkJoinTask framework
2,3
, has been devel-
oped and will be included in Java
TM
version 7. The
ForkJoinTask framework is well-suited for the paral-
lelization of recursive divide-and-conquer algorithms.
A given complex problem is divided into two or more
subtasks that are then solved in parallel. These sub-
tasks are in turn divided into parallel subtasks and so
1
http://jce.iaik.tugraz.at/
2
http://jcp.org/en/jsr/detail?id=166
3
http://gee.oswego.edu/dl/concurrency-interest/
on. This is repeated until the task is small enough to
be directly solved. The following listing shows how
this can be achieved in Java.
class SortTask extends RecursiveAction {
final long[] a;
final int lo;
final int hi;
SortTask(long[] a, int lo, int hi) {
this.a = a;
this.lo = lo;
this.hi = hi;
}
protected void compute() {
if (hi - lo < THRESHOLD)
sequentiallySort(a, lo, hi);
else {
int mid = (lo + hi) >>> 1;
invokeAll(new SortTask(a, lo, mid),
new SortTask(a, mid, hi));
merge(a, lo, hi);
}
}
}
2.3 Applied JCE Parallelizations
The objective of our work was to apply the two men-
tioned parallelization methods to selected algorithms
of the existing IAIK JCE implementation. This JCE
had not been originally designed with paralleliza-
tion in mind. Therefore, our first task was to deter-
mine those sections in the sequential code where par-
allelization is possible and where it actually makes
sense.
In general, the parallelization of sequential code
is no trivial task (Peierls et al., 2005). Researchers
try to solve this issue with automatic paralleliza-
tion tools and refactoring engines (e.g. (Dig et al.,
2009)(Rugina and Rinard, 1999)(Freisleben and Kiel-
mann, 1995)). Such tools are especially useful for
large applications with many lines of code where
manual refactoring becomes tedious and error prone.
In the case of cryptographic libraries, these tools are
often less effective. Cryptographic algorithms are
usually designed such that each calculation step de-
pends on the result of the previous step.
Furthermore, cryptographic algorithms often con-
tain numerous simple operations, like shift, add, or
xor. Although these operations could basically be
easily parallelized, the parallelization of such sim-
ple operations can have counter-productive effects re-
garding the performance gain due to parallelization
overhead.
Having these issues in mind, we have examined
the possible performance gain of cryptographic algo-
rithms through parallelization. Therefore, we have se-
lected the commonly used algorithms ’RSA key-pair
EMPLOYING MULTI-CORE PROCESSOR ARCHITECTURES TO ACCELERATE JAVA CRYPTOGRAPHY
EXTENSIONS
7

generation’, ’RSA cipher’, and ’ECDSA signature
verification’ for manual parallelization. For all in-
vestigated algorithms, both parallelization techniques
being described in Section 2.2 have been applied. In
the following subsections we explain how the three
selected cryptographic algorithms have been paral-
lelized.
2.3.1 RSA Key-pair Generation
The first cryptographic operation we have improved
in the course of this work was the RSA key-pair gen-
eration. The investigated JCE implements the key
generation algorithm that was published in (Silver-
man, 1997). According to this algorithm, the inves-
tigated JCE executes the following basic steps to gen-
erate all data required for building a CRT (Chinese
Remainder Theorem) compliant RSA key-pair.
1. Compute strong prime p
2. Compute strong prime q
3. Ensure that p is greater than q
4. p
1
= p − 1
5. q
1
= q − 1
6. φ = p
1
∗ q
1
7. Choose an appropriate public exponent pubExp
8. modulus = p ∗ q
9. privExpt = pubExp
−1
mod φ
10. dP = privExp mod p
1
11. dQ = privExp mod q
1
12. coe f = q
−1
mod p
After completion of these computation steps, all
data required to build an RSA key-pair are available.
A breakdown of the sketched algorithm reveals that
several major computation steps are independent and
hence can be scheduled in parallel. In more specific
terms, this applies to Step 1 and Step 2, Step 4 and
Step 5, as well as to Step 10 and Step 11. Obviously,
the two independent steps 4 and 5 consist of trivial
computations only. Hence, it can be expected that a
parallelization of these two steps would not increase
the algorithm’s performance significantly due to the
inherent parallelization overhead.
In order to parallelize the given RSA key-pair gen-
eration algorithm, we have therefore put the focus on
the computation of the two strong primes p and q,
and on the derivation of the values dP and dQ. We
have re-implemented the given algorithm by apply-
ing the two parallelization methods that have been in-
troduced in Section 2.2. This way, the performance
of the JCE’s RSA key-pair generation algorithm has
been increased significantly. More detailed informa-
tion about the achieved performance enhancements
are provided in Section 3 of this paper.
2.3.2 RSA Cipher
After successfully enhancing the performance of the
RSA key-pair generation algorithm we have analyzed
the RSA cipher algorithm. If possible, the RSA im-
plementation of the investigated JCE uses the Chinese
Remainder Theorem (CRT) to speed up the execution
of RSA encryption and decryption operations. The
following computation steps are executed by the JCE
to encrypt a given plain text message m with a given
private key using the Chinese Remainder Theorem.
1. c
11
= m mod p
2. c
1
= c
dP
11
mod p
3. c
21
= m mod q
4. c
2
= c
dQ
21
mod q
5. c
3
= (c
1
− c
2
) ∗coe f
6. c
4
= c
3
mod p
7. c = (c
4
∗ q)+ c
2
After completion of these computation steps, the
obtained result c represents the input data m being
RSA encrypted with the given private RSA key. A
breakdown of the sketched computation steps turns
out that Step 1 and Step 2 can be processed in parallel
to Step 3 and Step 4. Again, we have modified the
existing JCE in order to take advantage of the local-
ized potential for parallelization. Detailed informa-
tion about the performance improvements that have
resulted from modifications of the RSA cipher algo-
rithm are provided in Section 3.
2.3.3 ECDSA Signature Verification
ECDSA signature verification was the third JCE algo-
rithm that has been investigated in the course of this
work. Based on elliptic curve cryptography, ECDSA
allows for much smaller key sizes compared to the
conventional DSA algorithm and is therefore enjoy-
ing increased popularity. For our investigations we
have put the focus on the ECDSA signature verifica-
tion of a message m. To verify a given ECDSA signa-
ture consisting of the pair (r, s) with the given public
key Q
A
, the investigated JCE executes the following
computation steps.
1. Check if both, r and s are integers in the interval [1, n −
1] for n being the order of the curve’s base point G
2. e = HASH(m)
3. c = s
−1
mod n
4. u
1
= (e ∗ c) mod n
5. u
2
= (r ∗ c) mod n
6. Compute point (x
1
, x
2
) = u
1
∗ G + u
2
∗ Q
A
7. If r = x
1
mod n, the given ECDSA signature is valid
WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies
8

It is apparent that for instance Step 4 and Step
5 could be executed in parallel as these computa-
tion steps are completely independent. However, the
mathematical operations being executed in these steps
are not very complex. Hence, parallelization of these
steps would not increase the algorithm’s performance
significantly. The computationally most intensive op-
eration is actually executed in Step 6. Hence, we have
split this computation step into two independent com-
putations r
1
= u
1
∗ G and r
2
= u
2
∗ Q
A
. The results of
these computations are subsequently added in order
to retrieve the final result (x
1
, x
2
) = r
1
+ r
2
. Since the
computations of the intermediate results r
1
and r
2
are
independent, they can again be executed in parallel.
Due to the parallelization of these computation
steps, the overall performance of the JCE’s ECDSA
signature-verification algorithm could be improved
significantly. Detailed information about the gained
speed-up is provided in Section 3 of this paper.
2.3.4 Scalability Considerations
The overall goal of parallelization is to divide a given
computational problem into several sub tasks and ex-
ecute these tasks concurrently on different cores. As
the provided Java
TM
APIs do not make any limitations
regarding the number of existing cores, the achiev-
able speed-up theoretically grows linearly with the
number of available cores. However, in practice the
achievable speed-up actually depends on the paral-
lelized Java
TM
source code.
In all investigated algorithms, only two steps were
executable in parallel. Hence, the applied JCE en-
hancements are especially suitable for processor ar-
chitectures with two cores. Nevertheless, further po-
tential for parallelization could probably be found on
other levels of abstraction. However, as scalability
was not the main objective of our activities, further
optimizations of the JCE in terms of scalability are
regarded as future work.
3 PERFORMANCE ANALYSIS
The basic objective of this work was to evaluate
whether the performance of the investigated JCE can
be improved by employing multi-core architectures.
Therefore, implementations of three different crypto-
graphic algorithms have been manually revised and
parallelized. Details about the applied modifications
of the investigated JCE have been provided in Section
2. In a subsequent step, several tests have been con-
ducted in order to measure the effective speed-up that
has been gained from the applied modifications. The
measurement framework and the different measure-
ment environments that have been used for these tests
are introduced in this section. Furthermore, this sec-
tion illustrates the obtained results of the performance
analysis process and discusses basic findings.
3.1 Measurement Framework
The aim of the performed measurement series was
to measure the efficiency of the applied JCE paral-
lelization and the achievable computational speed-
up. To guarantee meaningful measurement results,
a common measurement framework has been devel-
oped. This framework has then been used to evaluate
improvements of different cryptographic algorithms
and to appropriately format the collected measure-
ment data.
Figure 1: Measurement Setup.
Fig. 1 shows the general measurement setup, on
which all measurement runs have been based on. The
core element of the setup is the developed measure-
ment framework, which provides a user interface,
through which measurement runs can be manually
controlled. The measurement framework itself has
access to three different instances of the investigated
JCE. The instance ’IAIK JCE Sequential’ represents
an unmodified default release of the JCE library and
acts as reference module. Measurements on modified
instances of the JCE are compared to measurements
on this reference implementation in order to evaluate
the efficiency of different modifications. The two JCE
instances ’IAIK JCE Parallel (Impl. 1)’ and ’IAIK
JCE Parallel (Impl. 2)’ comprise different versions of
parallelized cryptographic algorithms. In order to al-
low meaningful comparisons between the three avail-
able implementations, each modified cryptographic
algorithm has been tested on all three JCE instances
subsequently.
EMPLOYING MULTI-CORE PROCESSOR ARCHITECTURES TO ACCELERATE JAVA CRYPTOGRAPHY
EXTENSIONS
9
3.2 Measurement Systems
The modified JCE implementations and the devel-
oped measurement framework have been deployed
and tested on different measurement environments in
order to minimize the influence of environment and
system specific effects. Therefore, all measurements
have been performed on two different machines be-
ing equipped with different central processing units
(CPU) and different operating systems.
The first machine (System A) was equipped with
an Intel Mobile Core 2 Duo P8600 CPU (code name
’Penryn’) running at a clock frequency of 2.4 GHz.
Details about this CPU are provided in Table 1. Fur-
thermore, this machine was equipped with 3 GB of
random access memory (RAM). The installed operat-
ing system was Microsoft Windows XP (32bit) with
Service Pack 3. Due to the installed 32bit operating
system, all tests on this machine have been performed
with the 32bit version of the Sun Java
TM
Runtime En-
vironment (JRE) 7 only.
Table 1: System A - CPU characteristics.
Name Intel Mobile Core 2 Duo P8600
Package Socket P (478)
Clock frequency 2.40 GHz
Cores 2
Threads 2
The second machine (System B) was equipped with
an Intel Pentium D930 CPU (code name ’Presler’)
running at a clock frequency of 3 GHz. Further details
about this CPU are provided in Table 2. On System B,
2 GB of RAM were available. The system was run-
ning with the operating system Microsoft Windows 7
Enterprise (64bit). All measurements on this system
have been performed using 32bit as well as 64bit ver-
sions of the Sun Java
TM
Runtime Environment (JRE)
7.
Table 2: System B - CPU characteristics.
Name Intel Pentium D 930
Package Socket 775 LGA
Clock frequency 3.00 GHz
Cores 2
Threads 2
Hence, in total three measurement environments
(ME) were available. The first environment (ME1)
was System A and the 32bit version of Sun JRE 7.
The other two measurement environments were Sys-
tem B with the 32bit Sun JRE (ME2) and System B
with the 64bit Sun JRE (ME3), respectively.
3.3 Results
In order to evaluate the efficiency of the applied JCE
modifications, the three parallelized cryptographic al-
gorithms have been tested on all three available mea-
surement environments.
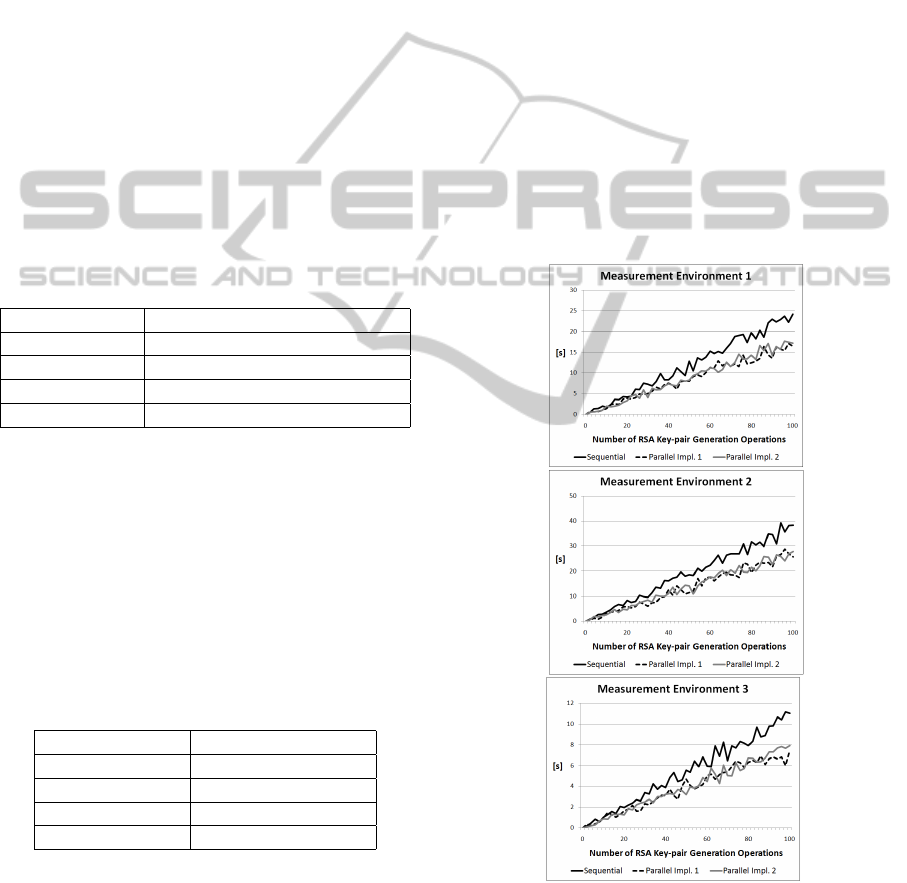
In the first measurement run, RSA key-pair gen-
eration operations have been performed on all avail-
able environments. Fig. 2 shows the result of this
measurement run. On all three measurement environ-
ments, usage of the parallelized JCE implementations
has led to a significant speed-up. At the same time,
it has turned out that the two alternative parallel im-
plementations basically lead to similar results. De-
pending on the particular measurement environment,
speed-ups between 1.35 and 1.41 have been reached
by using parallelized JCE implementations. Table 3
summarizes the achieved speed-up for RSA key-pair
generation operations in relation to the original se-
quential JCE implementation.
Figure 2: RSA Key-pair Generation (1024 bit) on Different
Measurement Environments.
In a second measurement run, the parallelized
RSA cipher algorithm has been evaluated. Therefore,
RSA cipher operations have been performed on all
WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies
10

Table 3: RSA Key-pair Generation - Speed-up.
JCE P I JCE P II
ME 1 1.39 1.35
ME 2 1.41 1.38
ME 3 1.40 1.37
three available JCE instances. Fig. 3 illustrates the
results of this measurement run. Again, usage of the
two parallelized JCE implementations has led to a sig-
nificant computational speed-up. Similar to the RSA
key-pair generation measurement run, there is no ob-
vious difference in the performance between the two
alternative parallel implementations.
Figure 3: RSA Encryption on Different Measurement Envi-
ronments.
Table 4 summarizes the observed speed-up that
has been gained due to the usage of the two paral-
lelized JCE instances. Depending on the particular
measurement system, the time consumption for RSA
encryption operations could be reduced by up to 43%.
Finally, the third measurement run has evaluated
the efficiency of the parallelized ECDSA algorithm.
Therefore, the time consumption of ECDSA signature
verification operations has been measured. Again,
measurements have been carried out for all three
available JCE implementations.
Fig. 4 shows the results of this measurement run.
Also for the ECDSA algorithm, the applied modifica-
tions have caused a significant computational speed-
up. While there is an obvious improvement compared
to the sequential JCE implementation, the two paral-
lel JCE instances basically led to similar results. The
achieved speed-up for ECDSA signature verification
operations on different measurement environments is
summarized in Table 5.
Table 4: RSA Encryption - Speed-up.
JCE P I JCE P II
ME 1 1.65 1.65
ME 2 1.74 1.74
ME 3 1.49 1.62
Figure 4: ECDSA Signature Verification on Different Mea-
surement Environments.
In general, all conducted measurement runs have
proven that parallelizing JCE implementations can
significantly reduce the processing time of crypto-
graphic algorithms. Depending on the investigated
EMPLOYING MULTI-CORE PROCESSOR ARCHITECTURES TO ACCELERATE JAVA CRYPTOGRAPHY
EXTENSIONS
11

algorithm and the used measurement environment,
parallel implementations have reduced the time con-
sumption of certain cryptographic algorithms by up to
43.93%.
This observation holds for both, systems with
32bit as well as 64bit Java
TM
Runtime Environ-
ments. Although systems with 64bit JREs have gen-
erally shown a better performance in terms of ex-
ecution time, computations on parallelized JCE in-
stances have been always faster than computations on
the unmodified sequential reference JCE implementa-
tion. Hence, the taken measurements have shown that
on any system the parallelized JCE instances perform
better than their unmodified sequential pendants.
Table 5: ECDSA Signature Verification - Speed-up.
JCE P I JCE P II
ME 1 1.67 1.67
ME 2 1.73 1.72
ME 3 1.76 1.78
4 CONCLUSIONS
With the emergence of multi-core processor architec-
tures, the demand for parallel software has increased.
Since programmers are used to write sequential soft-
ware for single core architectures, the development of
parallel software is usually challenging.
Due to the computational complexity of cryp-
tographic algorithms, the parallelization of crypto-
graphic implementations could significantly increase
their performance. In this work we have shown
that already minor manual adaptations of an exist-
ing sequential Java
TM
cryptography library can sig-
nificantly reduce the computing time of several cryp-
tographic algorithms when being executed on multi-
core architectures. In this paper we have shown how
to improve algorithms of an existing cryptographic li-
brary by applying parallelism. Furthermore, results of
measurements that have been conducted with the un-
modified JCE as well as with two different manually
parallelized JCE instances have been depicted.
The obtained results show that parallelizing cryp-
tographic Java
TM
libraries does definitely make sense.
Although only minor manual adaptations have been
applied in this work, speed-up factors of up to 1.78
could be reached. For future work it is planned to op-
timize the applied parallelization of the cryptographic
library. This could be achieved by either applying a
more sophisticated manual parallelization or by using
tools that try to automatically parallelize existing se-
quential source code.
Another potential for further performance increase
is the re-implementation of certain cryptographic al-
gorithms. In many cases, cryptographic algorithms
can be implemented in different ways. By choosing
an implementation that allows a high degree of paral-
lelization, the achievable speed-up on multi-core ar-
chitectures could probably still be increased. This ap-
proach has not yet been followed in the course of this
work but is regarded as topic for future work.
REFERENCES
Bridges, M. J., Vachharajani, N., Zhang, Y., Jablin, T., and
August, D. I. (2008). Revisiting the sequential pro-
gramming model for the multicore era. Micro, IEEE,
28(1):12–20.
Daemen, J. and Rijmen, V. (2002). The Design of Rijndael.
Springer-Verlag New York, Inc., Secaucus, NJ, USA.
Dig, D., Marrero, J., and Ernst, M. D. (2009). Refactoring
sequential java code for concurrency via concurrent li-
braries. In ICSE ’09: Proceedings of the 2009 IEEE
31st International Conference on Software Engineer-
ing, pages 397–407, Washington, DC, USA. IEEE
Computer Society.
Freisleben, B. and Kielmann, T. (1995). Automated
transformation of sequential divide-and-conquer algo-
rithms into parallel programs. Computers and Artifi-
cial Intelligence, 14:579–596.
Lea, D. (2005). The java.util.concurrent synchronizer
framework. Sci. Comput. Program., 58(3):293–309.
Peierls, T., Goetz, B., Bloch, J., Bowbeer, J., Lea, D., and
Holmes, D. (2005). Java Concurrency in Practice.
Addison-Wesley Professional.
Rugina, R. and Rinard, M. (1999). Automatic paralleliza-
tion of divide and conquer algorithms. In PPoPP ’99:
Proceedings of the seventh ACM SIGPLAN sympo-
sium on Principles and practice of parallel program-
ming, pages 72–83, New York, NY, USA. ACM.
Silverman, R. D. (1997). Fast generation of random, strong
rsa primes. CryptoBytes, 3(1):9–13.
Sutter, H. (2005). The free lunch is over: A fun-
damental turn toward concurrency in software.
http://www.gotw.ca/publications/concurrency-
ddj.htm.
WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies
12
