GRAPH-BASED MANAGEMENT OF COMMUNITIES

OF WEB SERVICE REGISTRIES

Olfa Bouchaala

1,2

, Mohamed Sellami

, Walid Gaaloul

, Samir Tata

TELECOM SudParis, CNRS UMR Samovar, Evry, France

Mohamed Jmaiel

University of Sfax, ReDCAD Laboratory, National School of Engineers of Sfax, Sfax, Tunisia

Keywords:

Web service registry, Registry community, Communities management.

Abstract:

Web services discovery represents a prominent step in the development process of B2B applications. In such

environment, the number of Web services as well as registries that are made available for use can be as many

as the large number of companies. Thus, the Web services discovery process will be time consuming. To

deal with this issue, one obvious solution is to group Web service registries into communities. However,

this solution can raise a managing issue since registries and communities are dynamic by nature. Our major

contribution in this paper is an approach for managing registries and communities to reconcile conﬂicts result

of the dynamic change aspect of Web service registries.

1 INTRODUCTION

Within a B2B context, we are interested in Web ser-

vice (WS) discovery in a distributed registry environ-

ment, where companies use WSs to achieve transac-

tions with their partners and offer online WSs. The

involved companies have to make their WSs accessi-

ble on the net and available for consultation through

WS registries. As a result, the number of WS reg-

istries can be very large. Therefore, WSs discovery

will be a cumbersome task. To deal with this prob-

lem and to address the large number of WS registries

and their poorly organized network, we propose to or-

ganize WS registries into communities. We deﬁne a

WS registry community as a set of registries offering

WSs providing similar functionalities. This organiza-

tion is based on a semantic model, that we call Web

Service Registry Description (WSRD) (Sellami et al.,

2010a). WSRD descriptions rely on the descriptions

of the WSs belonging to a given registry and ”seman-

tically aggregate” the WSs functionalities.

In a distributed registry network, each registry is

then described by a WSRD description. According

to their descriptions, registries will be virtually struc-

tured into communities (Sellami et al., 2010b). This

solution reduces the search space for a service re-

quester in the discovery process. However, it may rai-

se other issues mainly related to community manage-

ment. Indeed, communities and their members (i.e.

WS registries) are dynamic by nature. In fact, a new

WS description can be published in a registry and oth-

ers can be unpublished at any time. In the same way, a

registry can join a community or leave it according to

its convenience. Therefore, management mechanisms

are necessary to monitor these changes and reconcile

potential conﬂicts.

In this context, we propose a graph-based ap-

proach for managing communities of WS registries

which consists in a set of algorithms and managing

operations. The managing operations are pre and

post-conditions checking triggers and potential ef-

fects for each step of community life-cycle. The al-

gorithms are rather deﬁned for managing the registry

life-cycle steps. These algorithms and operations are

tested and validated using graph simulation.

This paper is organized as follows: in Section 2,

we start by a brief introduction of concepts of the

graph theory, we present our registry description

model, we provide our deﬁnition of registries com-

munities and present our approach for building such

communities. The graph based model, that we pro-

pose to facilitate the speciﬁcation of managing oper-

ations, is presented in Section 3. In Section 4, we

deﬁne managing algorithms and operations for reg-

Bouchaala O., Sellami M., Gaaloul W., Tata S. and Jmaiel M..

GRAPH-BASED MANAGEMENT OF COMMUNITIES OF WEB SERVICE REGISTRIES.

DOI: 10.5220/0003347400610070

In Proceedings of the 7th International Conference on Web Information Systems and Technologies (WEBIST-2011), pages 61-70

ISBN: 978-989-8425-51-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

istry and community life-cycles. The implementation

efforts are shown in Section 5. Finally, we conclude

our paper and we foresee some future works.

2 BACKGROUND

Since we model our WS registry community network

based on graph theory, we start by brieﬂy introducing

graph prerequisites and some of the special types of

graphs playing prominent role in our work. Then, we

present the WSRD semantic model used to describe a

registry. Afterwards, we present our community def-

inition and architecture. Finally, we present our ap-

proach for building communities.

2.1 Background on Graph Theory

We deﬁne our distributed registry network based on

the notations and concepts offered by graph theory.

Indeed, graphs are highly ﬂexible models for analyz-

ing a wide range of practical problems through a col-

lection of nodes and connections between them. A

given problem is then mathematically formalizedwith

a graph G, deﬁned as a pair of sets G = (V, E). V is

the set of vertices (or nodes) and E is the edge set

representing the network connections. The number of

vertices |V| of the graph G is its order. When G is not

the only graph under consideration, the vertex- and

edge-sets are denoted respectivelyV(G) and E(G).

A graph can be either directed or undirected. In

the ﬁrst case, each edge is an ordered pair of vertices.

In the second case, edges represent unordered pairs

of vertices. Both directed and undirected graphs may

be weighted by a weight function w : E −→ R assign-

ing a weight on each edge. A weighted graph is then

denoted G = (V,E,w).

2.1.1 Adjacency Matrix

The adjacency matrix A

of a given graph G = (V,E)

of order n is an n× n matrix A

= (a

i, j

) where

i, j



1 if (i, j) ∈ E

0 otherwise

In a weighted graph, the adjacency matrix can be

used to store the weights of the edges (McConnell,

2008). Hence, the values of the adjacency matrix for

G would be deﬁned as follows :

i, j







i, j

if (i, j) ∈ E

0 if i = j

∞ if (i, j) 6∈ E

2.1.2 Star Graph

Graphs are classiﬁed into different types according to

the nodes organization as well as the relationship be-

tween them. In this work, we use a particular type of

graphs, called star graphs. A star graph is a complete

bipartite graph K

1,k

or K

k,1

A graph G is called bipartite (or bigraph) (Bondy

and Murty, 2007) if its vertex set can be divided into

two subsets X and Y such that every edge joins a ver-

tex in X to another in Y. Such a graph is denoted

G = (X,Y,E). A bigraph is complete if every vertex

in X is joined to every vertex in Y. This is denoted

n,m

with n, m respectively the cardinality of X and

Y. If n = 1 or m = 1, G becomes a star graph.

2.1.3 Operations on Graphs

To simplify the management operations and algo-

rithms that we present in Section 4, we use some op-

erations deﬁned in graph theory. Since graphs are de-

ﬁned as pairs of vertex and edge-sets, we use the set-

theoretical terminology to deﬁne operations on and

between them. Among these operations, we remind

the addition/deletion of a vertex or an edge to/from a

graph and the complement of a graph.

The addition/deletion of a vertex v (resp. an

edge e) to/from a graph G = (V,E) yields to a

union/substraction of the vertex set V(G) and {v}

(resp. the edge set E(G) and {e}). We remind that the

deletion of a vertex v removes not only this vertex but

also all edges with this vertex as extremity. The result-

ing graph is then denoted G = (V\{v},E\{(u, v) ∈

E|u ∈ V}). The complement of a graph G = (V,E) is

a graph

G = (V,V × V\E) with the same vertices as

G but with only those edges that are not in G. G ∪ G

represents a complete graph.

2.2 WSRD: Web Service Registry

Description

In our context, we are dealing with private registries,

not public ones, belonging to a speciﬁc company.

Thus, we assume that all the services advertised by a

registry are homogenous in term of their business do-

main and semantics. In addition, since those services

have the same provider, we suppose that they use the

same semantic description language. To describe the

functionalities of a WS registry, we proposed in pre-

vious works (Sellami et al., 2010a) to use a semantic

model. This description, that we call Web Service

Registry Description (WSRD), results from the ag-

gregation of the different WSs functional descriptions

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies

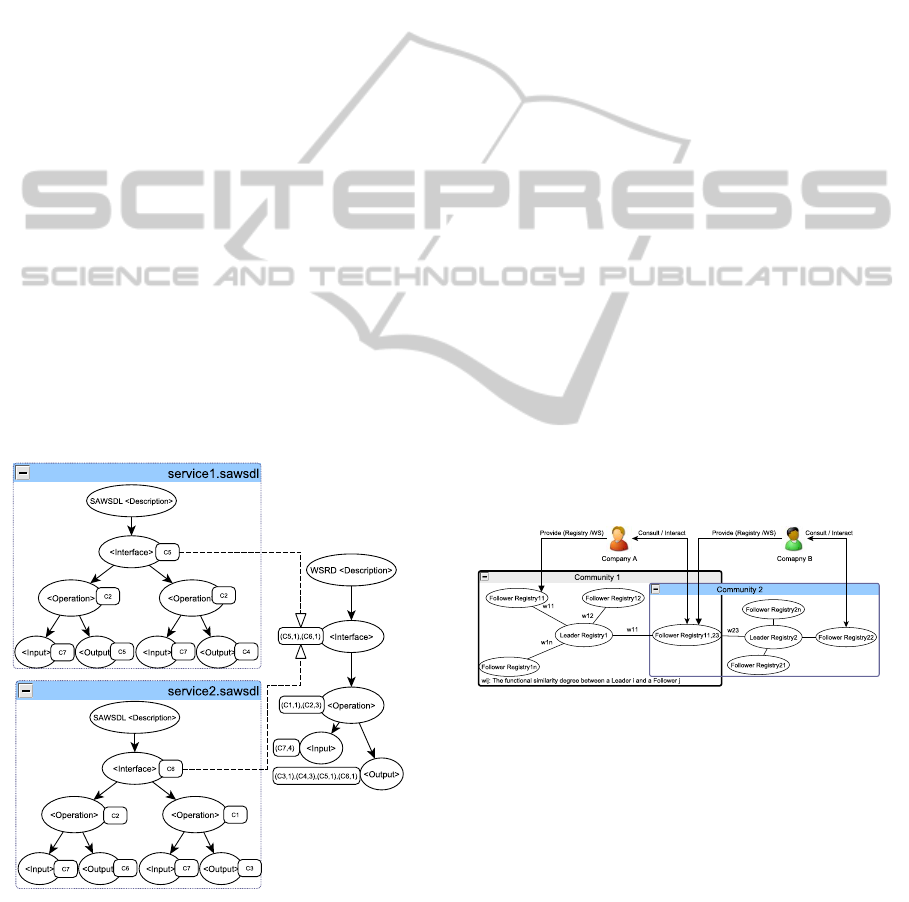
advertised by a registry. The registry description com-

puting process doesn’t ask for any explicit knowledge

from a registry provider. It is implicitly created using

only as input the WSs descriptions of that registry and

no further information are required.

In Figure 1, we consider an example of a registry

advertising only two semantic WS descriptions writ-

ten in SAWSDL (Lausen and Farrell, 2007). We sup-

pose that the used ontology is composed of 7 con-

cepts. Computing the registry’s WSRD decription

goes beyond three steps: (1) extracting the annotat-

ing concepts, (2) constructing the clouds of potential

mean concepts and (3) reducing the clouds. In Fig-

ure 1, we show an ”intermediate” WSRD graph de-

scription result of the ﬁrst step consisting in storing

the extracted concepts and the number of times they

were identiﬁed in the corresponding service descrip-

tion elements. The obtained WSRD ”intermediate”

graph is used in the second step for computing the

potential mean concepts of a WSRD description. A

mean concept (C

mean

) is the ontological concept an-

notating a WSRD element. A C

mean

is computed on

the basis of the extracted concepts and can be seen

as the medium of these concepts. The third step con-

sists in reducing the cloud of C

mean

in order to select

the median concept(s) which are the most similar to

the ones identiﬁed in the ﬁrst step. We use the Weak

reduction technique (Sellami et al., 2010a) to deduce

the resulting WSRD description graph.

Figure 1: Concept extraction.

2.3 Communities of WS Registries

The Oxford dictionary deﬁnes a community as ”a

group of people living together in one place hold-

ing certain attitudes and interests in common”. In

the WSs research ﬁeld, Benatallah et al. (Benatallah

et al., 2003) deﬁne a WS community as ”a collec-

tion of Web services with a common functionality al-

though different non-functional properties”. Zakaria

et al. (Maamar et al., 2007) consider a community as

”a means for providing a common description of a de-

sired functionality without explicitly referring to any

concrete Web service that will implement this func-

tionality at run-time”. In the same spirit, we deﬁne

a WS registry community as a set of registries offer-

ing WSs providing similar functionalities. So, a dis-

tributed registry network will be virtually structured

into communities and each registry belongs to at least

one community with a certain extent. We assign for

each registry a set of membership degrees indicating

its membership to the different communities. In each

community we associate to one registry the role of

leader and to the other members the role of followers

(Figure 2). The leader registry is the most represen-

tative registry of the community functionality. There-

fore, the leader plays a prominent role in managing

its community and its members. Obviously, a leader

for a community c

could be a follower for another

community c

and vice versa. The leader-follower

relationship within a community indicates the level of

similarity between the functionalities offered by both

of them.

Figure 2: Architecture of WS registries communities.

2.4 Building WS Registry Communities

A WS registry community will bring together reg-

istries offering similar functionalities. Since a WS

registry generally offers services proposing different

functionalities, it is difﬁcult to properly deﬁne in ad-

vance classes categorizing the functionalities of the

different registries. To organize WS registries into

communities, we used (Sellami et al., 2010b) a clus-

tering technique (where the different communities

will be deduced from the registry descriptions) rather

than a classiﬁcation technique (where the different

GRAPH-BASED MANAGEMENT OF COMMUNITIES OF WEB SERVICE REGISTRIES

communities have to be deﬁned in advance). When

using a dynamic clustering technique, the different

clusters (i.e. the WS registries communities) will be

identiﬁed from the given input data (i.e. the WSRD

descriptions) and each data point (i.e. WS registry)

will be assigned to one or many communities.

Since a registry can belong to different communi-

ties at the same time (Section 2.3), the use of an ex-

clusive clustering is inadequate for building registry

communities. Therefore, we proposed to use an over-

lapping clustering method to organize our distributed

registries into communities. Using such clustering

method, each data point (i.e. registry) represented

by its WSRD description may belong to two or more

communities with different degrees of membership.

Each WSRD description x will be represented as

a vector r

= [w

,... ,w

] where t is the total

number of concepts in the ontology used to annotate

the WSRD description. The weights of the different

= α× v

inter face

+β× v

operation

+δ× v

input

+λ× v

output

• v

inter face

= [e

,. . . , e

] representing the C

mean

of the

resulting WSRD

element.

• α, β, δ and λ are weights associated such as α+β+ δ+

λ = 1.

A distance measure is used to establish the degrees

of membership of each WS registry, represented by

the vector r

, to the different clusters. In this work,

we use the cosine similarity measure to establish the

similarity between two given vectors r

and r

(for-

mula (1)).

cosine(r

) =

· r

kkr

(1)

To deduce the distance from the cosine similarity

function, we use formula (2).

distance(r

) = 1− cosine(r

) (2)

More details about our WS registries clustering

approach can be found in (Sellami et al., 2010b).

3 MODELING COMMUNITIES

OF WEB SERVICE REGISTRIES

Communities and WS registries operate within a dy-

namic environment where changes are mainly initi-

ated by service and registry providers. The service

provider can publish or delete a WS. Similarly, the

registry provider can register its WS registry or dis-

mantle it at any moment. To keep the consistency of

our communities network against these events, man-

agement operations are needed. To facilitate the spec-

iﬁcation of these operations, we model the WS reg-

istry community network based on graph theory. In

this section, we introduce our model representing a

WS registry, a community and a community network.

3.1 Modeling a Web Service Registry

In this work, we refer to each WSRD description of a

WS registry by f. A registry can belong to different

communities at the same time. Thus, we assign to

a registry a set of membership degrees that we call

MEM. This set contains its membership degrees to

each community in the network. Accordingly, a WS

registry is deﬁned as follows:

Deﬁnition 1. A registry is deﬁned as a tuple r =

(id, f, MEM) where:

• id is the registry identiﬁer.

• f is a vector representing functionalities offered

by the advertised WSs within r.

• MEM represents the registry membership degrees

to the different communities in the network. It

is deﬁned as a binary relation on C × [0,1]. We

remind that a binary relation is a set of ordered

couples. MEM = {(c,d)|c ∈ C,d ∈ [0,1]} where:

– C is the community set

– d is the membership degree of the registry r to

the community c.

We deﬁne the domain and range of MEM ⊆ C× [0,1]

as:

dom(MEM) = {c|(c,d) ∈ MEM for some d ∈ [0, 1]}

ran(MEM) = {d|(c,d) ∈ MEM for some c ∈ C}

3.2 Modeling a Web Service Registry

Community

A community in our distributed registry environment

is mainly characterized by its mean functionality f

which represents the average of community registries

functionalities. Registries can enter and leave a com-

munity almost at any time. Besides, we ﬁx a thresh-

old

beyond of which a registry could belong to a

given community. As reported in section 2.3, we dis-

tinguish two kinds of registries (leader and follower)

based on their role inside a community. Therefore,

the set of community members (nodes) can be divided

into a singleton L = {l} representing the leader and a

set Fl = { fl

|i : 1..n} where n is the number of the

community followers. Thus, the community nodes

are modelled as a star graph G where nodes are reg-

istries and each edge represents the functional simi-

larity between the leader and a follower fl, fl ∈ Fl.

The similarity between the functionalities offered by

the leader and a follower can be computed using the

cosine function (Section 2.4, formula (1)). Hence, we

deﬁne a community as follows:

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies

Deﬁnition 2. A community is a tuple c = (id, f,G)

with:

• id is the community identiﬁer.

• f is a vector representing the mean functionality

of the community c.

• G = (L,Fl,E, w) is an undirected weighted star

graph where:

– L is the community leader: the registry having

the highest membership degree inside c.

– Fl is the set of community followers

– E ⊆ L× Fl is the set of edges

– w : E −→ [0, 1] is a weighting function repre-

senting the similarity between nodes.

3.3 Modeling the Community Network

So far, our distributed registry environment which is a

set of communities is modelled by a set of star graphs.

As the number of registries (nodes) can be very large

and a single registry can belong to many communi-

ties, the community management is a cumbersome

task. To deal with this problem and to have a global

view of the network, we deﬁne another graph CG,

called Community Graph, in which nodes represent

communities and edges are the relationships between

them. If two communities have at least one registry in

common, then there is an edge joining them. In this

case, we compute the distance between their vectors f

representing their mean functionalities. The distance

can be computed using formula (2) of Section 2.4.

The distance measure will be the weight of the edge

relating these two communities. Our distributed reg-

istry network is then deﬁned as follows:

Deﬁnition 3. The registry network is represented by

an undirected weighted graph CG = (C, E,w)

• C is a ﬁnite set of nodes. Each single node repre-

sents a registry community.

• E ⊆ C ×C is the set of edges (representing the

relationships between communities).

• w : E −→ [0,1] is a weighting function represent-

ing the distance between two given nodes.

4 MANAGING COMMUNITIES

In the following, we deﬁne the necessary management

operations to handle WS registries and WS registry

communities during their life cycles.

4.1 The Registry Life-cycle

A registry life-cycle starts when a registry provider

decides to register its WS registry in the network

(Figure 3 (1)). This registry joins the network (2)

and then joins the adequate communities accord-

ing to its offered functionalities (3). Since a service

provider can publish (4) or delete (5) a WS within

this registry, its WSRD description can change and an

update of the registry functionalities (6) is needed.

In such scenario, a suitability check of the registry

membership should be done: If the registry member-

ship degree is lower than a certain threshold

set by

the designer, it leaves the community (7) and joins

another one. Finally, the registry can leave the whole

network (8) if its provider decides to dismantle it (9).

In the following, we detail the steps (2), (3) and (6) of

the registry life-cycle.

4.1.1 Joining the Network

When a new WS registry r joins our distributed reg-

istry environment, its WSRD description should be

computed. After that, the registry can be guided to the

adequate communities according to its set of mem-

bership degrees MEM. MEM is computed by the

CommunitySelection algorithm (Algorithm 1). This

algorithm takes as input the current registry’s WSRD

description and it is essentially based on the com-

putation of the membership degree as the inverse of

the distance between the community mean function-

ality c. f and the registry functionalities r. f (line 2).

This distance measure is computed according to for-

mula (2) (Section 2.4). This algorithm outputs the set

of membership MEM containing the membership de-

grees of the current registry to the different communi-

ties in the network. Taking into account that the mem-

bership degree must be greater than the threshold

deﬁned above (line 4), the registry will be guided to

the adequate communities (line 5). If all membership

degrees are lower than

, a new community will be

created (Section 4.2.1).

Algorithm 1: CommunitySelection.

Require: r :registry

Ensure: r.MEM

1: for each community c ∈ C do

2: m ←− 1/distance(c. f,r. f)

3: r.MEM ←− r.MEM ∪ {(c,m)}

4: if m >

then

5: V(c.G) ←− V(c.G) ∪ {r}

6: end if

7: end for

GRAPH-BASED MANAGEMENT OF COMMUNITIES OF WEB SERVICE REGISTRIES

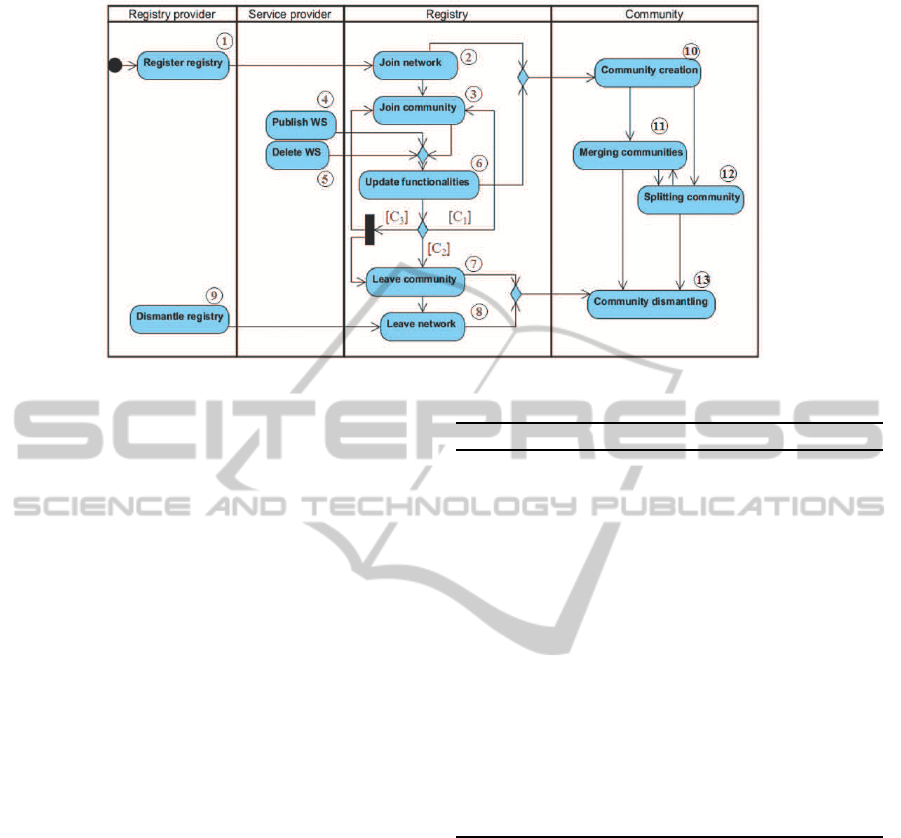
Figure 3: Communities management process.

4.1.2 Joining a Community

When a registry joins a community, it may have

a membership degree greater than the community

leader. In this case, the LeaderReselection algorithm

(Algorithm 2) should be applied. It checks either

or not the new registry will take the role of leader

in one of the communities it belongs to (line 1, 5).

This is done through a simple comparison between

the new registry’s membership degree and the com-

munity leader’s one (line 5). If the leader’s member-

ship degree is still the greatest, then we only link the

current registry with the community leader (line 6, 7).

Otherwise, we remove all followers-leader links (line

9,10,11), add the leader to the followers set (line 12),

the current registry takes the leader’s place (line 13)

and the community followers will be linked to the new

community leader (line 14,15,16).

4.1.3 Updating Registry Functionalities

We recall that the WSs advertised within a registry

frequently change (new WSs arrive, others leave).

Therefore, the registry functionalities have to be reg-

ularly updated. When a change occurs, the registry

can stay in the same community, leave or move from

a community to another. After a functionalities up-

date, a registry acceptance or denial in a community

happens according to the CommunityAcceptance al-

gorithm algorithm (Algorithm 3). By applying this

algorithm on a set of updated registries, the following

events can happen:

• E = E

′

, i.e. no changes occur in the set of com-

munity members, where E and E

′

are two sets of

members of a given community c, respectively be-

fore and after updating registries functionalities.

Algorithm 2: LeaderReselection.

Require: r: registry

1: for all Communities c ∈ dom(r.MEM) do

2: Let {l} ←− c.G.L

3: Let d

∈ [0,1] such that (c,d

) ∈ r.MEM

4: Let d

∈ [0,1] such that (c, d

) ∈ l.MEM

5: if d

and d

> d

then

6: c.G.Fl ←− c.G.Fl ∪ {r}

7: E(c.G) ←− E(c.G) ∪ {(r,l)}

8: else

9: for all fl ∈ c.G.Fl do

10: E(c.G) ←− E(c.G) − {(l, fl)}

11: end for

12: c.G.Fl ←− c.G.Fl ∪ {l}

13: c.G.L ←− {r}

14: for all fl ∈ c.G.Fl do

15: E(c.G) ←− E(c.G) ∪ {(r, fl)}

16: end for

17: end if

18: end for

• E ⊂ E

′

, i.e. some new registries join the set of

community members. (Figure 3.[C1])

• E

′

⊂ E, i.e. some registries leave the set of com-

munity members. (Figure 3.[C2])

• E * E

′

andE

′

* E, i.e. some new registries join

the set of community members and some others

leave. (Figure 3.[C3])

4.2 The Community Life-cycle

The main steps describing a community life-cycle re-

volvearound community creation, dismantling, merg-

ing and splitting. When the membership degrees of a

registry became lower than the threshold

for all

existing communities, a new community will be cre-

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies

Algorithm 3: CommunityAcceptance.

Require: r:registry, c:community

Ensure: (accept/deny)

1: Let d ∈ [0,1] such that (c, d) ∈ r.MEM

2: d ←− 1/distance(c. f,r. f)

3: if d >

then

4: return accept

5: else

6: return deny

7: end if

ated (Figure 3(10)). Also, a community will be dis-

mantled (13) if it becomes empty. Throughout a reg-

istry life-cycle, we check the similarity inside and be-

tween communities to ensure the principle goal of

clustering: minimizing the similarity between clus-

ters while maximizing it within each cluster. To guar-

antee this goal, a community can be merged (11) to

another one or split (12). In the following, we present

triggers and effects for each step.

4.2.1 Community Creation

A new community c

new

= (id, f,G) is established

automatically, if the membership degrees of a reg-

istry to all the existing communities are lower than

the threshold

. This situation necessarily implies

that c

new

provides a new functionality in the network.

This can happen when a new registry joins the net-

work (Section 4.1.2) or after an update of the reg-

istry’s functionalities (see Section 4.1.3). So the Pre-

condition for a community creation is modeled as:

∀d ∈ ran(r.MEM), d <

The registry r that triggered the community cre-

ation, will get the role of leader for the new commu-

nity c

new

. The community mean functionality c

new

. f

will be the same as the functionality r. f proposed by

the registry. Afterwards, the FollowersSelection algo-

rithm (Algorithm 4) will be executed to recruit fol-

lowers for the new community. In this aim, the mem-

bership degrees of existing registries to the new com-

munity are computed. These different actions form

the Post-condition for a community creation and are

modeled as follows: c

new

∈ V(CG)∧c

new

.G.L = {r}∧

new

. f = r. f ∧ c

new

.G.Fl = FolowersSelection(c

new

)

4.2.2 Community Dismantling

A community c is automatically dismantled; when

it becomes empty |V(c.G)| = 0 (all of its members

leave or no longer exist). This is the only condition

that triggers the disappearance of a community. This

Pre-condition is modeled as follows: c ∈ V(CG) ∧

|V(c.G)| = 0.

After deleting a community, we must check the

Algorithm 4: FollowersSelection.

Require: c

new

: community

Ensure: c

new

.Fl : Follower Set

1: for all Communities c ∈ C do

2: for all Registries r ∈ V(c.G) do

3: Let {l} ←− c

new

.G.L

4: m ←− 1/distance(c

new

. f, r. f)

5: r.MEM ←− r.MEM ∪ (c

new

,m)

6: if m >

then

7: c

new

.G.Fl ←− c

new

.G.Fl ∪ {r}

8: E(c

new

.G) ←− E(c

new

.G) ∪ {(l,r)}

9: end if

10: end for

11: end for

12: return c

new

.Fl

Post-condition stating that c is not the extremity of

any edge in the community graph CG: c 6∈ V(CG) ∧

∀c

∈ V(CG), (c, c

) 6∈ E(CG)

4.2.3 Merging Communities

The natural idea that ﬁrst comes to mind when decid-

ing which communities to merge is closeness. Based

on the graph CG and assuming that (c

) ∈ E(CG)

(Section 3.3), this issue can be speciﬁed as follows:

w(c

) < ξ such that ξ ∈ [0, 1] a threshold beyond

of which two communities can be merged.

However, the closeness is computed using a geo-

metrical distance without taking into account the reg-

istries dispersion. Thus, an exception can take place

when communties centers are close to each other but

not dense in the middle way between centers. i.e. few

registries in the intersection (Figure 4(a)) or commu-

nities are completely separated (Figure 4(b)). As a

consequence the closeness condition is necessary to

check the similarity between communities function-

alities but not sufﬁcient.

(a) (b)

Figure 4: Distance between clusters centers (Zhang and

Shin, 2005).

Thus, we deﬁne the communities merging pre-

condition by adding another condition to the close-

ness one. This second condition checks if a com-

munity is included in another one. Our resulting

Pre-condition will be: c

∈ V(CG), ∃c

|w(c

) <

ξ ∧ V(c

.G) ⊂ V(c

.G). When this pre-condition is

satisﬁed for two communities, they will be merged

into a new one called c

merg

. The center of c

merg

GRAPH-BASED MANAGEMENT OF COMMUNITIES OF WEB SERVICE REGISTRIES

computed as the weighted average of both communi-

ties centers c

. f and c

. f :

merg

. f =

. f × nb

+ c

. f × nb

+ nb

(3)

Where:

• nb

= #{r|(c

) ∈ r.MEM∧(c

) ∈ r.MEM∧

≥ d

}, the number of registries in the intersec-

tion of c

and c

and having a greater membership

degree to c

• nb

= #{r|(c

) ∈ r.MEM∧(c

) ∈ r.MEM∧

≥ d

}, the number of registries in the intersec-

tion of c

and c

and having a greater membership

degree to c

Figure 5: Merging pre-condition.

As a consequence of the merging step, the com-

munity c

merg

is added to the graph CG and both com-

munities c

and c

are deleted. Thereby, all edges

whose ends are one of these two communities are re-

moved too. This Post-condition is modeled as fol-

lows: V(CG) = (V(CG) − {c

}) ∪ {c

merg

}

4.2.4 Splitting a Community

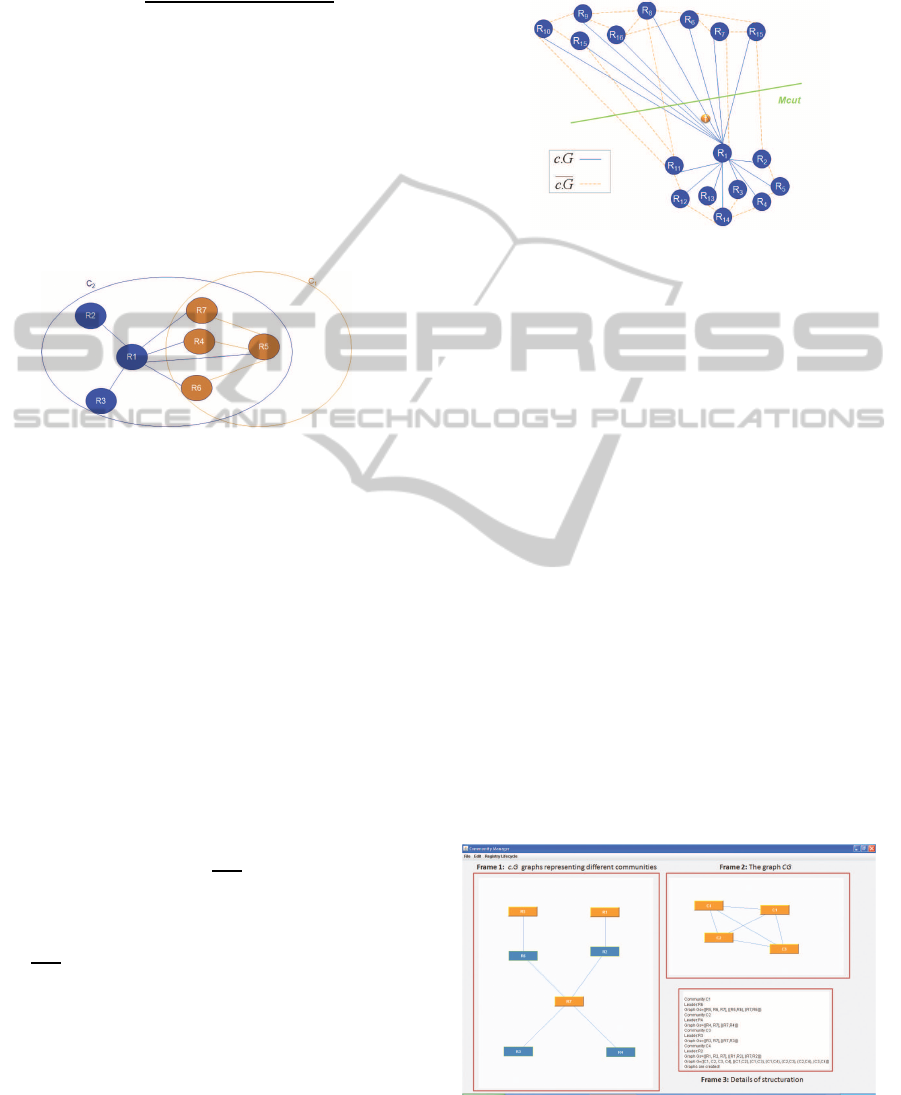
A community is automatically divided if it becomes

sparse. The community sparsity describes a non den-

sity in the center vicinity and a dispersion between

members (Figure 6). If this pre-condition is satisﬁed,

this issue can be observed as a graph partitionning

problem. Indeed, we consider a community c rep-

resented with its undirected weighted star graph c.G

which represents the similarity relationship between

the leader and its followers. c.G is the complement of

c.G (Section 2.1.3) and is also a weighted graph rep-

resenting similarity relationships between followers.

The weighted adjacency matrix of the complete graph

c.G∪

c.G contains all similarity weights between each

pair of community members (Section 2.1.1). An algo-

rithm which suits well to our needs taking as input a

weighted adjacency matrix of an undirected weighted

graph is the Mcut algorithm (Ding et al., 2001) which

proposes a graph partition method based on min-max

clustering principle: the similarity between two sub-

graphs is minimized while the similarity within each

subgraph is maximized. Figure 6 shows how this al-

gorithm is applied on a community c that satisﬁed the

splitting pre-condition.

Figure 6: Splitting a community using Mcut algorithm.

5 IMPLEMENTATION

To test the feasibility of our approach, we simulate

WS registry communities using graphs. Indeed, we

implemented a Community Manager (Figure 7) based

on the Jgraphtjava library (Jgrapht, 2003).

To validate the proposed algorithms and manag-

ing operations, we consider the following scenario:

We generate 700 SAWSDL descriptions using the se-

mantic description generator presented in (Chabeb

et al., 2010). These descriptions are organized into

7 registries such that each one contains 100 descrip-

tions. We compute the WSRD description of each

registry using the WSRDGen implemented in (Sell-

ami et al., 2010a). Each description is modeled with a

vector f = [w

,...w

] computed as shown in sec-

tion 2.4. These vectors represent the input of the clus-

tering method (Sellami et al., 2010b) which outputs

the mean functionality vectors {c. f|c ∈ C} and the

membership degrees of each registry to different com-

munities {r.MEM|r ∈ R}, with R the set of registries

in the network.

Figure 7: Community Manager.

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies

The vectors r. f, c. f and r.MEM, such that r ∈ R

and c ∈ C, are saved in an XML ﬁle representing ini-

tialization data for our Community Manager in order

to build the graphs modeling the communities and the

registries (Figure 7). In Frame 1, we present the graph

composed by the set of graphs c.G representing com-

munities. The leader of each community is repre-

sented by a blue rectangle. In Frame 2, we represent

the graph CG representing our community network.

As reported in Section 4, the main triggers of dy-

namic changes are service and registry providers. In

the following, we introduce these changesto test man-

aging algorithms and operations.

Adding a Registry. In order to test Community-

Selection and LeaderReselection algorithms,

we add a new registry in the network repre-

sented by its vector f=[0.234 0.314 0.048 0.181

0.534]. The Community Manager assigns an

identiﬁer to this new registry (r

) and then

compute its membership degrees r

.MEM =

{(c

,0.1943),(c

,0.282),(c

,0.2759),(c

,0.2479)}.

MEM is compared with

= 0.1. The new

registry belongs to all the existing communities.

At this level, the LeaderReselection algorithm

assigns the role of follower for r

in each com-

munity it belongs to. If we change

to 0.3,

we notice that all membership degrees of r

the existing communities are lower than

. In

this case, the community Manager cheks the

community creation pre-condition and estab-

lishes automatically a new community by adding

a new vertex to the CG graph. Accordingly,

the FollowersSelection algorithm is executed

selecting followers for r

which assumes the role

of leader in this new community.

Dismantling a Registry. The community c

is com-

posed by only two registries: r

the leader and

its follower (Figure 7). By dismantling r

, the

LeaderReselection algorithm is applied assigning

to be the leader. By dismantling r

, the com-

munity c

is automaticaly dismantled since the

dismantling pre-condition is satisﬁed.

Updating Registry Functionalities. The Commu-

nityAcceptance algorithm is tested through an

update of registry functionalities f. The update

is done if a service provider publish , unpublish

or modify a WS description advertised within

this registry. Using the updated graph of Frame

1 result of the addition of r

to the network

and assuming that

= 0.1, we ﬁrst update

’s functionalities. r

leaves the community c

because its membership to this community is now

lower than

. Actually, c

is composed of r

and r

. We notice that c

is included in c

, c

and c

. The merging pre-condition is partially

satisﬁed. However, we must check that the

weights of edges whose ends are c

and one of the

communities c

, c

and c

are lower than ξ = 0.2

(Section 3.3). c

satisﬁes this condition. Thereby,

and c

are merged into a new community c

These scenarios show the feasibility and validity

of our algorithms as well as managing operations used

to handle registry and community life cycles. In fact,

they execute well and automatically call each other

after every change.

6 RELATED WORK

To enhance the WS discovery process in a private

registries network, we use a functionality-driven ap-

proach to organize them into communities. Such a

registry network organization needs to be regularly

managed to ensure the consistency of the communi-

ties. In this paper, we are interested in the manage-

ment phase of registry communities. As far as we

know, this work is the ﬁrst attempt to manage commu-

nities of WSs registries. Indeed, several WS discov-

ery approaches in distributed registry environments

(Sellami et al., 2010c; Sivashanmugam et al., 2004;

Xu and Chen, 2007) structure their networks as clus-

ters but did not provide management mechanisms for

their clusters. In this section, we overview some re-

lated efforts in the ﬁeld of managing communities that

helped us tailor our approach.

In (Paik et al., 2005), Paik et al. present the WS-

catalogNet framework allowing to group e-catalogs

having similar domain into communities, build rela-

tionships between them and manage them constantly.

The system offer monitoring functionalities and man-

aging operations to restructure a community network

according to the user interaction. Therefore, au-

thors model the community network and then specify

pre-conditions and effects for each operation based

on the graph-based model they have deﬁned (Paik

et al., 2002). However, authors employ a classiﬁca-

tion technique to organize communities, while we use

a dynamic clustering one. Furthermore, we use the

functionality criterion to structure communities rather

than business domain.

Medjahed and Bouguettaya (Medjahed and

Bouguettaya, 2005) propose an approach to organize

WSs into communities depending on their domain

of interest. A community is an instance of an

ontology metadata called community ontology and

is described by a set of generic operations. In this

context, community providers can add, delete or

modify some generic operations. Service providers,

GRAPH-BASED MANAGEMENT OF COMMUNITIES OF WEB SERVICE REGISTRIES

in turn, can delete a WS from a community or make

its operations temporarily unavailable. Thus, authors

propose a P2P approach to manage these changes.

However, their operations are described informally

compared to our management operations.

In (Maamar et al., 2009), Maamar et al. discuss

the dynamic nature of WS community and focus on

potential conﬂicts. They propose in (Subramanian

et al., 2007) an approach to engineer WSs commu-

nities in order to reconcile these potential conﬂicts.

This approach is based on the Community develop-

ment protocol which is interested in managing com-

munities in term of attracting and retaining WSs, cre-

ating and dismantling communities. Similarly to our

approach, communities are organized according to

WSs functionalities. However, this approach did not

propose a model and their operation descriptions are

rather informal.

7 CONCLUSIONS

In this paper, we proposed an approach for manag-

ing communities of WSs registries. We ﬁrst deﬁned

a model to facilitate the managing step. Then we

identiﬁed the main steps of registry and community

life-cycles. Afterwards, we speciﬁed managing op-

erations and algorithms based on the model that we

have proposed. Finally, we implemented a Commu-

nity Manager to test and validte these algorithms and

operations using graph simulation. Experiments show

that our algorithms and managing operations execute

well. The splitting operation has not been tested since

its pre-condition is not yet speciﬁed. Indeed, we used

different methods to detect the sparsity criterion in a

given community such as standard deviation of a stat-

ical series but each one represents an exception. As

part of our short term perspectives, we plan to specify

a pertinent pre-condition for splitting operation. Fur-

thermore, we foresee to implement these algorithms

on top of the platform P2P JXTA (JXTA, 2004) in or-

der to test the precision/time ratio of our approach.

REFERENCES

Benatallah, B., Sheng, Q. Z., and Dumas, M. (2003). The

self-serv environment for web services composition.

IEEE Internet Computing, 7:40–48.

Bondy, J. A. and Murty, U. S. R. (2007). Graph Theory.

Springer London.

Chabeb, Y., Tata, S., and Ozanne, A. (2010). Yasa-m: A se-

mantic web service matchmaker. In AINA 2010, April

20-23, Perth, Australia.

Ding, C. H. Q., He, X., Zha, H., Gu, M., and Simon, H. D.

(2001). A min-max cut algorithm for graph partition-

ing and data clustering. In ICDM ’01, pages 107–114,

Washington, DC, USA. IEEE Computer Society.

Jgrapht (2003). Jgrapht. http://www.jgrapht.org/.

http://www.jgrapht.org/.

JXTA (2004). Jxta. https://jxta.dev.java.net/.

Lausen, H. and Farrell, J. (2007). Semantic annota-

tions for WSDL and XML schema. W3C recom-

mendation, W3C. http://www.w3.org/TR/2007/REC-

sawsdl-20070828/.

Maamar, Z., Lahkim, M., Benslimane, D., Thiran, P., and

Sattanathan, S. (2007). Web services communities -

concepts & operations -. In WEBIST’2007.

Maamar, Z., Sattanathan, S., Thiran, P., Benslimane, D.,

and Bentahar, J. (2009). An approach to engineer

communities of web services - concepts, architecture,

operation, and deployment. IJEBR, 9(4).

McConnell, J. J. (2008). Analysis of algorithms: an active

learning approach. Jones and Bartlett publishers.

Medjahed, B. and Bouguettaya, A. (2005). A dynamic

foundational architecture for semantic web services.

Distributed and Parallel Databases, 17(2):179–206.

Paik, H.-Y., Benatallah, B., and Hamadi, R. (2002). Dy-

namic restructuring of e-catalog communities based

on user interaction patterns. World Wide Web,

5(4):325–366.

Paik, H.-Y., Benatallah, B., and Toumani, F. (2005). Toward

self-organizing service communities. IEEE Trans-

actions on Systems, Man, and Cybernetics, Part A,

35(3):408–419.

Sellami, M., Bouchaala, O., Gaaloul, W., and Tata, S.

(2010a). WSRD: A web services registry description.

In NOTERE’10, May 31- June 2, Tozeur, Tunisia.

Sellami, M., Gaaloul, W., and Tata, S. (2010b).

Functionality-driven clustering of web service reg-

istries. In SCC 2010, Miami, Florida, USA.

Sellami, M., Gaaloul, W., Tata, S., and Jmaiel, M. (2010c).

Using recommendation to limit search space in web

services discovery. In AINA, pages 974–981. IEEE

Computer Society.

Sivashanmugam, K., Verma, K., and Sheth, A. P. (2004).

Discovery of web services in a federated registry en-

vironment. In ICWS’04, San Diego, California, USA,

pages 270–278. IEEE Computer Society.

Subramanian, S., Thiran, P., Maamar, Z., and Benslimane,

D. (2007). Engineering communities of web services.

In Kotsis, G., Taniar, D., Pardede, E., and Ibrahim,

I. K., editors, iiWAS, volume 229 of books@ocg.at,

pages 57–66. Austrian Computer Society.

Xu, B. and Chen, D. (2007). Semantic web services dis-

covery in p2p environment. In ICPPW ’07, page 60.

IEEE Computer Society.

Zhang, H. and Shin, D.-G. (2005). Objective function based

fuzzy clustering. Technical report, University of Con-

necticut.

WEBIST 2011 - 7th International Conference on Web Information Systems and Technologies