Document Clustering using Multi-objective Genetic

Algorithm with Different Feature Selection Methods

Jung Song Lee, Lim Cheon Choi and Soon Cheol Park

Division of Electronics and Information Engineering

Chonbuk National University, Jeonju, South Korea

Abstract. Multi-objective genetic algorithm for the document clustering is pro-

posed in this paper. The researches of the document clustering using k-means

and genetic algorithm are much in progress. k-means is easy to be implemented

but its performance much depends on the first stage centroid values. Genetic

algorithm may improve the clustering performance but it has the disadvantage

to trap in the local minimum value easily. However, Multi-objective genetic al-

gorithm is stable for the performances and avoids the disadvantage of genetic

algorithms in our experiments. The several feature selection methods are ap-

plied to and compared with those clustering algorithms. Consequently, Multi-

objective genetic algorithms showed about 20% higher performance than oth-

ers.

1 Introduction

Recently the document clustering draws attention to the information retrieval field

since large amounts of documents are presented. One of the good ways to handle the

large amount of documents is to make clusters by the similar ones. It is called the

document clustering [1, 2]. In that area the research using k-means and genetic algo-

rithms has been well known.

k-means algorithm [3] which was studied by MacQueen [4] is the simplest method

starting with the first stage centroid values. The similarity of documents is calculated

either by the euclidean distance or the cosine similarity. The newly produced clus-

tered documents redefine the cluster centroid and then make another set of new clus-

ters. This process repeats itself until the algorithm is terminated. This algorithm is

easy to implement and its process is fast so that it is widely used not only in the in-

formation retrieval but also many academic fields. However, it has the problem in

which its performance much depends on the first stage centroid values.

Another document clustering algorithm is genetic algorithm. It is now actively

studied [5]. The document clustering using genetic algorithm adopts the concept of

genetic evolution by which the elements requiring for clustering correspond to the

individual, chromosome, and gene respectively. As the generation evolves repetitive-

ly, it produces the suitable document cluster through objective function. The perfor-

mance of genetic algorithm exceeds that of k-means algorithm. However, the genetic

algorithm has some problems to define objective function evaluating a generation. If

Lee J., Choi L. and Park S..

Document Clustering using Multi-objective Genetic Algorithm with Different Feature Selection Methods.

DOI: 10.5220/0003351401010110

In Proceedings of the International Workshop on Semantic Interoperability (IWSI-2011), pages 101-110

ISBN: 978-989-8425-43-0

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

the inappropriate objective function is used it has the disadvantage of trapping into

the local minimum value easily in the algorithm.

In this paper, Multi-objective genetic algorithm is applied to the document cluster-

ing in order to solve the problems of both k-means and genetic algorithms. In addtion,

various feature selection methods are applied in order to reduce the number of execu-

tion time and to enhance the accuracy of the clustering.

This paper is organized as follows. The next section describes the method solving

the Multi-objective optimization problem by using the genetic algorithm. Section 3

shows about the document clustering using the Multiple-objective genetic algorithm

proposed in this paper. Section 4 explains experimental results. Section 5 concludes

and discusses future work.

2 Multi-objective Genetic Algorithm

2.1 Multi-objective Optimization Problem

There exist more problems which should satisfy several objective functions than

those satisfying a single objective function in the many fields [6]. Multi-objective

optimization problem is to find the solution optimizing several objective functions

and it is defined as (1).

min / max ( ) { ( ), ( ), ... , ( ) }

, ( , , ... , )

FX f X f X f X

XSX xx x

∈=

(1)

where F(X) is set of the objective function and X indicates n variables for the optimi-

zation on the variable space S. As shown in Fig. 1, X=(x

, x

) on the variable space S

can be changed into f

(X) and f

(X) expressed in the object function set F(X) on the

objective function space Y [7]. The objective function space Y has the following prob-

lems: First, each objective function is difficult to be compared. Second, each objec-

tive function has close relationship with others. So, as one function is improved better

the other becomes worse. That is, generally it is impossible to optimize all objective

functions at the same time. To avoid these problems, the non-dominance relation is

used to get the proper solution and this solution is called as the Pareto optimal solu-

tion [8].

Fig. 1. Variable Space and Objective Function Space.

102

2.2 Pareto Optimal Solution

Most excellent solution among all candidate solutions can be called as the optimal

solution in the single objective optimization problem. However, in the Multi-

objective optimization problem, as for the solution of one any kind of the optimal

solution cannot become to all objective functions. For this, the Pareto optimal solu-

tion is used [9]. The Pareto optimal solution can be obtained using the non-

dominance relation as in (2). If (2) is satisfied for a minimization problem the solu-

tion x is better than the solution y and it is expressed as x > y. It calls that x dominates

y and x is the non-dominate solution. These non-dominate solutions are called as the

Pareto optimal solution or the Pareto front and expressed as P in Fig. 1.

)()(:}, ... ,2 ,1{ and

)()(:}, ... ,2 ,1{

yfxfKj

yfxfKi

Syx

<∈∃

≤∈∀

∈

(2)

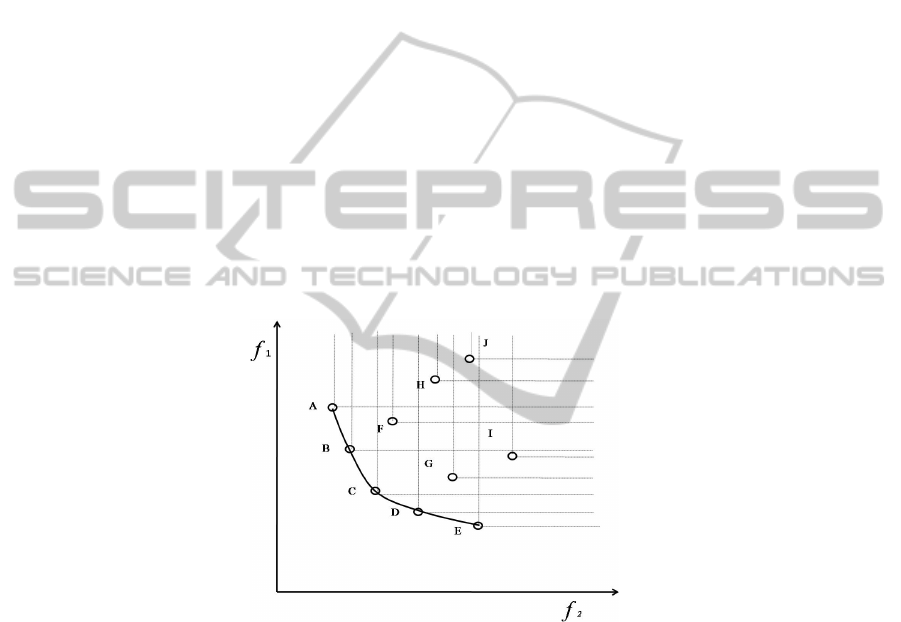
For example, in Fig. 2, A ~ J represent the solutions at the objective space trans-

formed from the variable space by F(X). A is clearly superior to H when assuming to

the minimization problem. In addition, A can refer to dominate H. If this relation is

applied, it is shown that A,B,C,D and E are superior to the others solutions and

A,B,C,D and E are the Pareto optimal solutions.

Fig. 2. Pareto optimal solutions according to the non-dominate relation.

2.3 Genetic Algorithm

Genetic algorithm proposed by the Holland [10] and Goldberg [11] is the algorithm

modeling the principles of the natural environments that is the dominant gene has

more chance to be selected for next generation [12]. Genetic algorithm searches out

the more suitable solution as the generation evolves by using evolution operators such

as selection, crossover and mutation.

Fitness function is the important factor to determine the convergence speed of the

algorithm and the accuracy of its solution, judging the overall performance [13].

103

However the algorithm may have the problem to trap in local minimum value easily

according to the improper fitness function. In order to avoid this problem of genetic

algorithms, Multi-objective genetic algorithm is applied to the document clustering in

this paper which is one of Multi-objective optimization problems.

2.4 Multi-objective Genetic Algorithms

There are two main algorithms to solve the Multi-objective optimization problem.

One is the method to use the incline of the objective function space, the other to con-

vert the several objective functions to the one objective function using the weighted

value. However, these methods have some disadvantages. First, they are dependent

on the initial search space. Second, they are unable to deviate from the local mini-

mum value and multiple solutions are unable to be found. It is genetic algorithm to be

paid attention to solve this disadvantage.

Multi-objective genetic algorithm can make multiple solutions which are close to

the Pareto optimal solutions [14]. The algorithms proposed till present for this pur-

pose are use to Pareto ranking evaluation method or Weighted-sum approach. Pareto

ranking evaluation method is the technique which determines the ranks based on the

superiority or inferiority relation of the solutions. Weighted-sum Approach is the

technique is to convert Multi-objective function with the weighted value to the single

objective.

Recently, NSGA-II expanding Non-dominated Sorting Genetic Algorithm

(NSGA) is preferred among the methods using the Pareto ranking evaluation. NSGA-

II minimizes the complicated computational complexity and maximizes the diversity

of the solutions. Moreover the elite preserve strategy has been introduced to separate-

ly manage the optimal solution discovered in the evolutionary process. It makes Mul-

ti-objective optimization process rapid and reduces the loss of the optimal solutions

[15, 16].

The operation process of Multi-objective genetic algorithm is identical with genet-

ic algorithm. However, it is different in that the candidate solution of next generation

is produced by using the non-dominate relation.

3 Document Clustering using Multi-objective Genetic Algorithms

In this paper, the document clustering based on Multi-objective genetic algorithm

employs in order to reduce the inclination of local minimum value. In addition, per-

formances of the algorithms are compared, applying the various objective functions to

the document clustering.

3.1 Chromosome Encoding

In order to get the optimal solutions for the document clustering, data should be close

to gene structure through the encoding process. In the previous research the cluster

centroid vector has been widely used as the gene [5].

104

In this paper a chromosome as shown in (3). It is defined as the combination of

the genes that corresponds to the document index number d of a document. Each gene

is encoded by the integer of K (number of the cluster group) range in the first stage as

shown in (3).

Chromosome

= { g

, g

, . . . , g

}

= { 1 ~ K }

(3)

Each gene indicates the cluster group. For example, assuming that the initial cluster

group number K is 3, as shown in (4) the first document is allocated to the second

cluster, the second document to the third cluster and the third document to the first

cluster, and so on.

Chromosome

= { 2, 3, 1, 1, 1, 2, 3, 3, 1} (4)

3.2 Evolution Operators

In this paper the evolution operators used in Multi-objective genetic algorithms is as

follows.

Selection: NSGA-II which offers one of the Pareto optimal solutions is used. NSGA-

II choosing the elite preserve strategy basically executes the tournament selection

operation.

Crossover: The multi-point crossover is used. The multi-point crossover expanded

through the two-point crossover produces the child nodes out of the parent combina-

tion as shown in Fig. 3.

Fig. 3. Multi-point crossover.

Mutation: The mutation uses the probability mutation computation. A probability is

given to each gene of the entity which is selected and mated. A gene less than a cer-

tain arbitrary value is randomly changed. The new entity is then created.

3.3 Fitness Function

The objective function controls the overall performance of genetic algorithm as the

standard which can determine how the present generation comes close to a solution.

In this paper, the various objective functions are applied to solve the document clus-

tering.

Clustering validity index is used as the objective function. This index is an evalua-

tion standard in order to appraise the results of the clustering validity, showing either

the minimum value or the maximum value when the optimum clusters are generated.

105

The clustering validity indexes used in this paper are CH (Calinski and Harabasz)

index [17] and DB (Davis and Bouldin) index [18].

The CH index is appropriate to cluster documents as the maximum value is

searched by using inter-group variance and between-group variance. It is shown in

(5).

1−

−

WGS

BGSS

(5)

where BGSS stands for Between Group Sum of Squares and WGSS stands for Within

Group Sum of Squares. n is the number of documents, k is the number of clusters.

The DB index is a function of the ratio of the sum of within-cluster scatter and in-

ter-cluster separation. Its maximum value is considered as the proper condition when

evaluating the cluster with the euclidean distance, while its minimum value with the

cosine similarity. It is as shown in (6).

max( )

jji

DB R

≠

∑

(6)

where n

is number of clusters. S

and S

are the average similarities of documents in

cluster centroids, i and j respectively. M

is the similarity between the cluster centro-

ids, i and j.

3.4 Feature Selection

One of the main problems of the document clustering is that the dimension of the

document by term matrix increases as the number of documents increases. This caus-

es that the computational complexity increases and the execution time grows longer

drastically. There are many features, in which an influence writes on all document set

that is, a term and the clustering accuracy falls [19].

In this paper, 3 feature selection methods are applied and they are as follows.

Document Frequency: Document Frequency(DF) means the frequency in which one

term appears in all document set. In this method, the terms with higher DF values are

counted as the test terms and it reduces the number of dimensions. This method is

simple and shows the good performance.

Term Contribution: Term Contribution(TC) is the similarity of the all documents

for one term t. It is defined as shown in (7) [20].

∑

≠∩

×=

jiji

dtfdtftTC

),(),()(

(7)

where f (t,d) is the tf *idf value of term t in document d.

106

Term Frequency Variance: The quality of the term t can be defined as TfV(Term

Frequency Variance). It is defined in (8) [21].

∑∑

⎥

⎦

⎤

⎢

⎣

⎡

−=

jjt

tfTfV

(8)

where tf

is the frequency of the term t in the document d

, n is the number of docu-

ments.

4 Experimental Results

Three algorithms, k-means, genetic algorithm and Multi-objective genetic algorithm

are tested and evaluated their performances for document clustering.

The Reuters-21578 text collection is used as an experimental dataset. 200 docu-

ments are chosen from 4 topics (coffee, trade, crude, and sugar) of the dataset. F-

measure is used to determine the accuracy of the clustering results and it is defined as

shown in (9).

RecallPrecision

RecallPrecision2

measureF

=−

(9)

The number of population in our GA and MOGA are 300. The algorithms are termi-

nated when the number of generations reaches to 600 or when the iterations without

improvement reach consecutive 30.

In our experiments, three feature selection methods are used in order to reduce the

number of dimensions of terms. The feature selection methods are document frequen-

cy (DF) like in (6), Term Contribution (TC) like in (7) and Term Frequency Variance

(TfV) like in (8).

1000 2000

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

No. Of Dimensions Of Terms

(

)

F - Measre

K-means

GA(DBC)

MOGA(DBC-DBE)

MOGA(DBC-CH)

Fig. 4. Clustering results with DF.

107

Fig. 4 is the document clustering performance results with DF. The performances

of all algorithms are highest when the number of dimensions of terms is 100.

Particu-

larly MOGA(DBC-CH) where DBC is stands for DB index with cosine simility and

CH is stands for CH index shows the highest performance among the algorithms.

MOGA (DB-CH) shows the performance about 16% better than k-means, 24% than

GA(DBC), and 25% than MOGA(DBC-DBE) where DBE is stands for DB index

with euclidean distance.

Fig. 5 is the document clustering performance results with TC. The algorithms ex-

cept MOGA(DBC-DBE) have the highest performances when the number of dimen-

sions of a term is 100. MOGA (DBC-CH) shows the performance about 10% higher

than k-means, 21% than GA(DBC), and 22% than MOGA(DBC-DBE).

1000 2000

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.75

0.8

No. Of Dimensions Of Terms

(

)

F - Measure

K-means

GA(DBC)

MOGA(DBC-DBE)

MOGA(DBC-CH)

Fig. 5. Clustering results with TC.

0 1000 2000

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

No. Of Dimensions Of Terms (TfV)

F - Measure

K-means

GA(DBC)

MOGA(DBC-DBE)

MOGA(DBC-CH)

Fig. 6. Clustering results with TfV.

Fig. 6 is the document clustering performance results with TfV. The performances

of the algorithms are highest when the number of dimensions of a term is 100.

108

MOGA (DBC-CH) shows higher performance than the others. The performance

of MOGA (DBC-CH) is about 17% higher than k-means, 26% than GA(DBC) and

28% than MOGA(DBC-DBE).

Table 1 presents the clustering algorithm performances according to the different

feature selection methods. The performances of GA(DBC) and MOGA(DBC-DBE)

show lower than k-means for all of the feature selection methods. Because the genetic

algorithms often trap in the local minimum value, it makes the performances worse.

All the cases of our experiments, it has best performances when TfV is used for fea-

ture selection method and when the number of dimensions of a term is 100.

Table 1. Performances of the algorithms according to the different feature selection methods.

Clustering

Algorithms

DF TC TfV

100 500 1000 2000 100 500 1000 2000 100 500 1000 2000

K-means 0.68 0.60 0.55 0.51

0.7

0.64 0.60 0.57 0.72 0.65 0.60 0.55

GA(DBC) 0.64 0.44 0.50 0.47

0.7

0.45 0.45 0.46 0.80 0.46 0.45 0.45

MOGA

(DBC-DBE)

0.58 0.48 0.47 0.51

0.5

0.57 0.47 0.43 0.57 0.53 0.51 0.49

MOGA

(DBC-CH)

0.86 0.76 0.73 0.68

0.7

0.71 0.71 0.71 0.90 0.80 0.73 0.77

5 Conclusions and Future Works

In this paper, we introduce Multi-objective genetic algorithm for the document clus-

tering and show its higher performances comparing others. Multi-objective genetic

algorithm shows higher performance than k-means and genetic algorithms. The algo-

rithm using the DB index and the CH index with the cosine similarity as the objective

function has superior results to the other algorithms. In addition, when applying the

feature selection methods to the algorithm, the performances are much improved.

Especially the TfV method shows the highest performance improving about 19%

more than others.

The document clustering using Multi-objective genetic algorithm isn't still discov-

ered in our knowledge. More various cluster indices will be tried as objective func-

tions to prove the high performance of the algorithm in near future. Also, we would

like to find the elements to make high performance in the document clustering keep-

ing studying the relationship between cluster indices.

Acknowledgements

This research was supported by Basic Science Research Program through the Nation-

al Research Foundation of Korea(NRF) funded by the Ministry of Education, Science

and Technology (2010-0011997).

109

References

1. H. Frigui, R. Krishnapuran.: A robust compettive clustering algorithm with application on

computer vision. IEEE Trans. Pattern Anal. Mach. Intell. 21 (1999) 450-465.

2. W. B. Croft, D. Metzler and T. Strohman.: Search Engines Information Retrieval in Prac-

tice. Addison Wesley. (2009).

3. S. Selim and M. Ismail.: k-means-type algorithm generalized convergence theorem and

characterization of local optimality. IEEE Trans. Pattern Anal. Mach Intell. Vol. 6 (1984)

81-87.

4. J. B. MacQueen.: Some Methods for clssification and Analysis of Multivariage Observa-

tion. Proceedings of 5-th Berkeley Symposium on Mathematical Statistics and Probability.

Berkeley. University of California Press. (1967) 281-297.

5. W. Song and S. C. Park.: Genetic algorithm for text clustering based on latent semantic

indexing. Computer s and Mathematics with Applications. Vol. 57 (2009) 1901-1907.

6. A. Osyczka.: Multicriteria optimization for engineering design. Design Optimization

(J.S.Gero, ed.). (2985) 193-227.

7. S. K. Park, S. B. Lee, W. C. Lee.: Goal-Pareto based NSGA-Ⅱ Algorithm for Multiobjec-

tive Optimization. Conference Korea Information and Communications. Vol. 32 No. 11

(2007) 1079-1085.

8. Jared L. Cohon and David H. Marks.: A Review and Evaluation of Multiobjective Pro-

gramming Techniques. Water Resources Research. Vol. 11. No. 2 (1975) 208-220

9. Censor, Y.: Pareto Optimality in Multiobjective Problems. Appl. Math. Optimiz. Vol. 4.

(1977) 41-59.

10. Holland J. H.: Adaption in natural and artificial systems. Ann Arbor: Univ. Michigan Press.

(1975).

11. Goldberg D. E.: Genetic algorithm in search, Optimization and Machine Learning. Addi-

son-Wesley. New York (1989).

12. L. D. Davis.: Handbook of Genetic Algorithms. Van Nostrand Reinhold (1991).

13. U. Maulik, S. Bandyopadhyay.: Genetic algorithm based clustering technique. Patten Rec-

ognition. Vol. 33 (2000) 1455-1465.

14. K. Deb.: Multi-Objective using Evolutionary Algorithms. John Wiley & Sons, Ltd. Chiche-

ster, England. (2001).

15. K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan.: A Fast Elitist Multiobjective Genetic

algorithm: NSGA-Ⅱ . IEEE Transaction on Evolutionary Computation. Vol. 6. No. 2.

(2002) 182-197.

16. http://mikilab.doshisha.ac.jp/dia/research/mop_ga/moga/3/3-5-5.html.

17. Calinski T. and Harabasz, J.: A Dendrite Method for Cluster Analysis. Communucations in

Statistics. Vol. 3. No. 1 (1974) 1-27.

18. Davies D.L, and Bouldin, D.W.: A Cluster Separation measure. IEEE transactions on Pat-

tern analysis and Machine Intelligene. Vol. PAMI 1. No. 2. (1979) 224-227.

19. Y. Yang and J.O. Pedersen.: A comparative study on feature selection in text categoriza-

tion. In Proc. ICML. (1997) 412-420.

20. Tao Lie, Shengping Liu, Zheng Chen, Wei-Ying Ma.: An evaluation on Feature Selection

for Text Clustering.

21. J. Kogan, C. Nicholas, and V. Volkovich.: Text mining with information-theoretical clus-

tering. Computing in Science and Engineering. (2003).

110