Document Clustering based on Genetic Algorithm

using D-Individual

Lim Cheon Choi and Soon Cheol Park

Division of Electronics and Information Engineering

Chonbuk National University, Jeonju, South Korea

Abstract. Document clustering using genetic algorithm shows good perfor-

mance. However the genetic algorithm has problem of performance degradation

by premature convergence phenomenon. In this paper, we proposed the docu-

ment clustering based on Genetic Algorithm using D-Individual (DIGA) to

solve this problem. Genetic algorithm is based on the diversity of population

and the capability to convergence. Success of genetic algorithm depends on

these two factors. If we use these factors efficiently, we can get a better solution

in reduced execution time. We apply DIGA to Reuter-21578 text collection and

demonstrate the effect of our clustering algorithm. The results show that our

DIGA has better performance than traditional clustering algorithms (K-means,

Group Average and genetic algorithm) in various experiments.

1 Introduction

The researches of document clustering are actively progressing for analysis and appli-

cation of mass information. The document clustering is to group the documents which

are similar in a set of documents without prior information.

The clustering algorithms are classified to the hierarchical clustering algorithm

and the non-hierarchical clustering algorithm based on grouping method [1],[2]. K-

means clustering algorithm is one of the non-hierarchical clustering algorithms [3].

Group Average clustering is one of the hierarchical clustering algorithms [2]. These

two clustering algorithms are fast in execution and easy to understand but do not

achieve the highest results [1],[2]. To solve it, genetic algorithm which is one of ar-

tificial intelligent algorithms has been applied to the document clustering and it shows

good results [4],[5].

Genetic algorithm is optimization algorithm using natural selection and evolution

operation. Genetic algorithm depends on the diversity of individuals and the capabili-

ty to convergence [4],[5],[6]. Capability to convergence of genetic algorithm has

weakness that is premature convergence phenomenon. The premature convergence

phenomenon is cause of depress the performance of genetic algorithm [7].

In this paper we propose the document clustering based on genetic algorithm using

the individuals which have the feature information of document clusters. The algo-

rithm has better performance and shorter execution time than the general Genetic

Algorithm.

Choi L. and Park S..

Document Clustering based on Genetic Algorithm using D-Individual .

DOI: 10.5220/0003351601110118

In Proceedings of the International Workshop on Semantic Interoperability (IWSI-2011), pages 111-118

ISBN: 978-989-8425-43-0

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

This paper is organized as follows. The next section describes the document clus-

tering using genetic algorithm. Section 3 presents the principle of DIGA. Section 4

explains experiment setting, evaluation approaches, results, and analysis. Section 5

concludes and discusses future work.

2 Document Clustering using Genetic Algorithm

Genetic Algorithm(GA) is based on the principles of the natural selection and the

survival of the fittest [6],[8]. Basic components of GA are gene, chromosome, indi-

vidual and fitness function. Individual is set of chromosomes characterized by genes.

Basic operations of GA are selection, crossover and mutation. GA makes the better

solution by these operations and components [4],[5].

Fig. 1 shows that the structure of individual which is one of basic components in

Genetic Algorithm for Document Clustering(GADC). As shown in Fig. 1 each gene

present the cluster number for one document in the document data set. In population

Initialization step, the cluster numbers generated randomly from 1 to k (where k is the

number of clusters).

Fig. 1. Structure of Individual in GADC.

GADC consists of Population Initialization, Fitness Function and basic operations

(selection, crossover, mutation). Fig. 2 shows that the GADC process. Each module in

the process is explained as follows

Fig. 2. GADC process.

Population Initialization. Suppose GADC has P individuals. Each individual has the

information of the cluster which a document belongs to. In population initialization

each document in assigned to a cluster randomly. The number of individuals P influ-

ences the performance and the execution time of GADC.

Selection Operation. Selection operation of GADC is quality proportion roulette

wheel selection one. (1) shows the definition of quality proportion roulette wheel

112

selection. After each individual is evaluated the best individual has t times more sur-

vival chance than the worst individual.





−



(



−



)

t−1

,t>1

(1)

where C

means selection probability of current individual, f

the fitness of current

individual, f

the worst fitness of set of individuals and f

the best fitness in individ-

uals . In our experiment, t equals to 3.

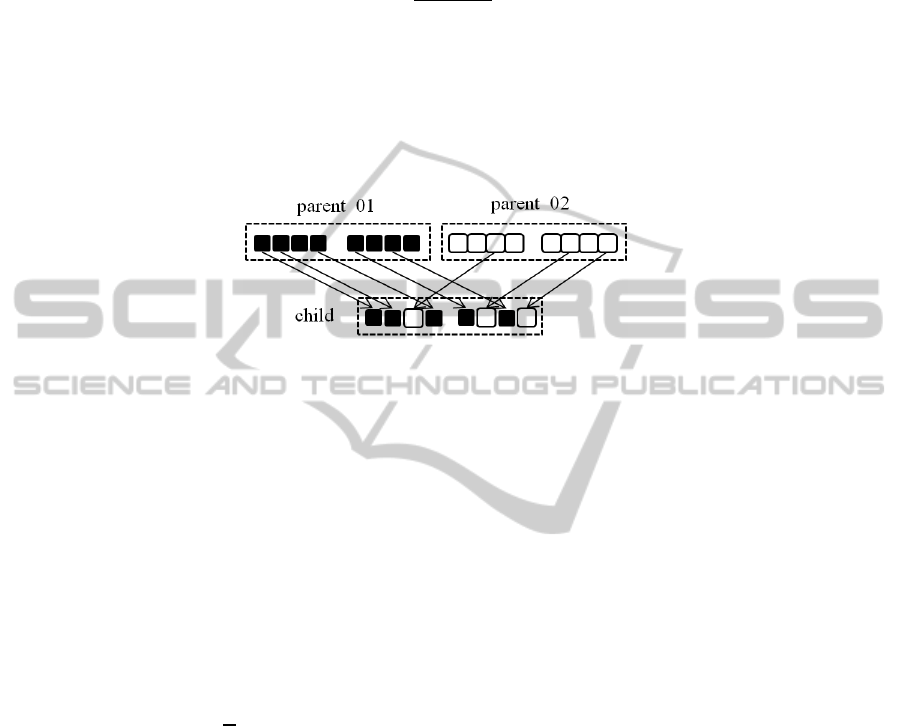
Crossover Operation. Crossover operation uses gene information of parent popula-

tions to generate new population. Crossover operation of GADC uses uniform cros-

sover operation in this paper as shown in Fig. 3.

Fig. 3. Uniform crossover.

In the uniform crossover scheme, genes in the chromosome are compared between

two parents. There genes are swapped with a fixed probability. We use 0.5 as the

fixed probability value.

Mutation Operation. Mutation operation produces the features which are not at the

parent features. The failure mutations are select out and the successful mutations

contribute to the improvement the quality of population. Mutation operation of

GADC is typical variation. In the typical variation scheme the information of gene is

randomly changed with a fixed probability (0.015).

Fitness Function. The individuals are evaluated by fitness function if they are good

or not. The fitness value is calculated by in the GADC by the average similarity of all

documents in a cluster [9],[10]. (2) shows that the formula of the Fitness Function.

Fitness =

AveSim



,whereAveSim



= Sim(d







)

























(2)

where k is the number of clusters and NC

the number of documents in ith cluster. d

is jth document in ith cluster. The similarity function Sim(d

) is cosine value be-

tween d

and d

. In this paper we use cosine similarity for Sim(d

) [9],[10].

3 Document Clustering based on Genetic Algorithm

using D-Individual

Sometimes genetic algorithm makes the result not enough to solve the problem. That

is cause of low performance and called premature convergence phenomenon [7]. In

113

this paper proposed the genetic algorithm using D-Individual (DIGA) to solve the

phenomenon. D-Individual is generated from GADC. (It is first introduced in this

paper). Fig. 4 shows the flowchart of DIGA. The process of DIGA is almost like that

of GADC. The only difference is using the D-individual in the Population Initializa-

tion. The other operations of DIGA, selection, crossover and mutation are the same in

the operations of GADC.

Fig. 4. Flowchart of DIGA.

Fig. 5. Generating process of D-individual in DIGA algorithm.

Population Initialization of DIGA. DIGA generates the first individuals by using the

D-Individuals. D-Individuals have the feature information of document clusters. Us-

ing D-Individuals we can make individual which has a higher possibility of evolution.

Fig. 5 shows the generating process of D-Individual in DIGA. DIGA decides

M(number of D-Individuals) and P(number of individuals). M and P influence DIGA

114

performance and execution time. DIGA can have better performance in short time

compare with traditional GA depends on the M and P. An experiment and result anal-

ysis about this are covered in more detail in Chapter 4.

4 Implementation and Results

This paper proposes the document clustering based on the genetic algorithm using D-

Individual. For estimating its performance, the Reuter-21578 text collection set is

used. Three Topic-Sets are experimented and four subjects were allocated to each

Topic-Set. Each subject has 50 documents, so that a Topic-Set has 200 documents.

Fig. 6 shows the Topic-Sets and subjects.

Topic-Set 1

earn, gnp, cocoa, gas

Topic-Set 2

coffee, crude, sugar, trade

Topic-Set 3

grain, crude, earn, ship

Fig. 6. Topic-Sets and Subjects.

As shown Fig. 6, 4 subjects in a Topic-Set are less related so that each subject

clearly distinguished each other. To evaluate the clustering performances, F1-measure

defined as in (3) is used

F1 − Measure =

2 × Pricision × Reccall

Pricision + Recall

(3)

The performances and execution time of GADC depends on the number of individu-

als as well as those of DIGA are depends on the number of individuals and the num-

ber of D-Individuals. Fig. 7 and 8 shows the difference of the GADC and DIGA per-

formances and execution times depending upon P(number of individuals) and

M(number of D-Individuals).

From result of Fig. 7 we can see that the DIGA shows a better performance than

GADC when P is the same. But these results are not enough because DIGA has long-

er execution time than the GADC as shown in Fig. 8. So we need more comparison

and analysis.

Fig. 9 shows the comparison of performance of DIGA and GADC. From Fig. 9 we

can see DIGA has better performance than GADC in same execution time.

The K-means clustering algorithm, the Group Average clustering algorithm and

GADC are compared to evaluate the proposed clustering algorithm, DIGA. Fig. 10

demonstrates the performance of clustering algorithms on each Topic-Set. It clearly

shows that DIGA has better performance than others. GADC shows better perfor-

mance than both K-means and Group Average clustering algorithms.

115

Fig. 7. GADC and DIGA performance depending upon P and M.

Fig. 8. GADC and DIGA execution time depending upon P and M.

Fig. 9. Performance of DIGA and GADC by the execution time.

116

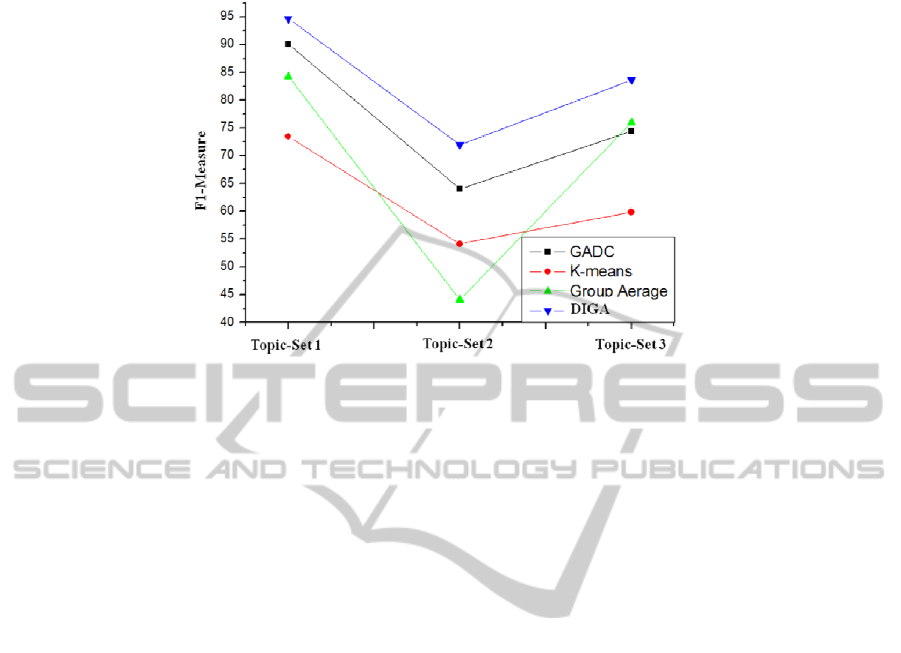
Fig. 10. Performance of clustering algorithm on each Topic-Set.

5 Conclusions

In this paper we have proposed the document clustering based on the genetic algo-

rithm using D-Individual. Our DIGA demonstrates the best performance among the

currently used clustering algorithms such as K-means clustering and Group Average

clustering. Moreover, DIGA has the higher performance and shorter execution time

than the general GADC. In this research, we find some meanings about D-individual

which have the feature information of document clusters, that helps traditional genetic

algorithm become more fast and accurate. DIGA has weakness of taking a long ex-

ecution time due to the complexity still. Regardless of execution time, our experi-

ments convince that DIGA shows the most accurate result in document clustering.

Acknowledgements

This research was supported by BK21 Project and Basic Science Research Program

through the National Research Foundation of Korea(NRF) funded by the Ministry of

Education, Science and Technology (2010-0011997).

References

1. B. Y. Ricardo and R. N. Berthier.: Modern information retrieval, Addison Wesley, 1999.

2. Christopher D. Manning, Prabhakar Raghavan & Hinrich Schütze, Introduction to Informa-

tion Retrieval, 2008.

117

3. S. Selim and M. Ismail, "K-means-type algorithm generalized convergence theorem and

characterization of local optimality", IEEE Trans. Pattern Anal. Mach Intell. vol. 6, pp. 81-

87, 1984.

4. W. Song, S. C. Park, Genetic algorithm-based text clustering technique, LNCS 4221 (2006)

779_782.

5. W. Song, S. C. Park, "Genetic algorithm for text clustering based on latent semantic index-

ing", Computers and Mathematics with Applications, vol. 57, pp. 1901-1907, 2009

6. U. Maulik, S. Bandyopadhyay, "Genetic algorithm- based clustering technique", Patten

Recognition. vol. 33, pp. 1455-1465, 2000.

7. J. Andre, P. Siarry, T. Dognon An improvement of the standard genetic algorithm fighting

premature convergence in continuous optimization, Advances in Engineering Software 32

49-60, 2001.

8. L. D. Davis, "Handbook of Genetic Algorithms", Van Nostrand Reinhold, 1991.

9. Xin Yao, Yong liu and Guangming Lin: Evolutionary Programming Made Faster. IEEE-

Trans, Evolutionary Computation, Vol. 3, No. 2 (1999).

10. D. L. Davies, D. W. Bouldin, A cluster separation measure, IEEE Trans. Pattern Anal.

Intell. 1 (1979) 224_227.

11. Csaba Legany, Sandor Juhasz, Attila Babos, “Cluster validity measurement techniques”,

“Knowledge Engineering and Data Bases”, Vol 5, pp. 388-393, 2006.

118