IMPROVING GEOMETRIC HASHING BY MEANS

FEATURE DESCRIPTORS

Federico Tombari and Luigi Di Stefano

DEIS-ARCES, University of Bologna, Bologna, Italy

Keywords:

Geometric hashing, Feature matching, Object recognition.

Abstract:

Geometric Hashing is a well-known technique for object recognition. This paper proposes a novel method

aimed at improving the performance of Geometric Hashing in terms of robustness toward occlusion and clutter.

To this purpose, it employs feature descriptors to notably decrease the amount of false positives that generally

arise under these conditions. An additional advantage of the proposed technique with respect to the original

method is the reduction of the computation requirements, which becomes signiﬁcant with increasing number

of features.

1 INTRODUCTION

AND PREVIOUS WORK

Geometric Hashing (GH) (Lamdan and Wolfson,

1988) is a powerful and popular technique for object

recognition. GH relies on interest points, or features

(e.g. corners, edge points, ...) to detect the presence

of a particular object, or shape, in an image. GH is

divided into two main stages: Modeling (ofﬂine) and

Recognition (online) stage. During the ﬁrst, given the

object to be detected, a set of features is extracted

from a model image. Then, for each feature pair (x

), or basis, all features are transformed to a new co-

ordinate systems where one axis goes through x

and

, and the unit length is the distance between x

and

. For each basis, all feature coordinates are stored

into a quantized histogram, or Hash Table. During the

Recognition stage, features are ﬁrst extracted from the

image under analysis (hereinafter also referred to as

target image). Then, for a feature pair, all the features

of the target image undergo the same transformation

as done for the model image, so that each transformed

coordinate pair casts a vote for the bases that were ac-

cumulated in the hash table bin they fall into. If a

basis gets a number of votes higher than a pre-deﬁned

threshold, then that basis identiﬁes the presence of the

object model into the target image, otherwise another

feature pair is taken under evaluation. This approach

detects objects under similarities (i.e. translation, ro-

tation and scaling), while to deal with afﬁne trans-

formations each basis has to be formed by a feature

triplet instead of a pair (Lamdan and Wolfson, 1988).

To above-describedmethod can be detect the presence

of multiple object models in the target image, i.e. by

considering (model,bases) pairs in both the online and

ofﬂine stages.

Later studies (Grimson and Huttenlocher, 1990;

Lamdan and Wolfson, 1991) have highlighted that

GH is particularly sensitive to the presence of clut-

ter and occlusions. In particular, in presence of many

spurious features originating from a cluttered back-

ground, the necessary use of a high number of bases

(which must be taken proportional to the number of

possible feature pairs) can easily cause false posi-

tives, i.e. false matches due to consistent accumula-

tion of a high number of erroneous votes (this phe-

nomenon is also known as data collision (Chum and

Matas, 2006)). This issue is worsened by the presence

of occlusions. In fact, even though in principle GH

can deal with partial occlusions (Lamdan and Wolf-

son, 1988), in practice when too many object features

are occluded the few visible ones cannot accumu-

late enough evidence to grant detection (Simon and

Meddah, 2006), especially in presence of data colli-

sions due to clutter. Accurate probabilistic analysis

of the error induced by GH can be found in (Grimson

and Huttenlocher, 1990; Lamdan and Wolfson, 1991).

Another disadvantage of the use of GH is the com-

putational time and memory requirements, which do

not scale well with the number of features (Iwamura

et al., 2007). As for the former, GH has a computa-

tional complexity of O(n

) (worst case), n being the

number of extracted features from the target image

(Lamdan and Wolfson, 1988).

419

Tombari F. and Di Stefano L..

IMPROVING GEOMETRIC HASHING BY MEANS OF FEATURE DESCRIPTORS.

DOI: 10.5220/0003355104190425

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 419-425

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

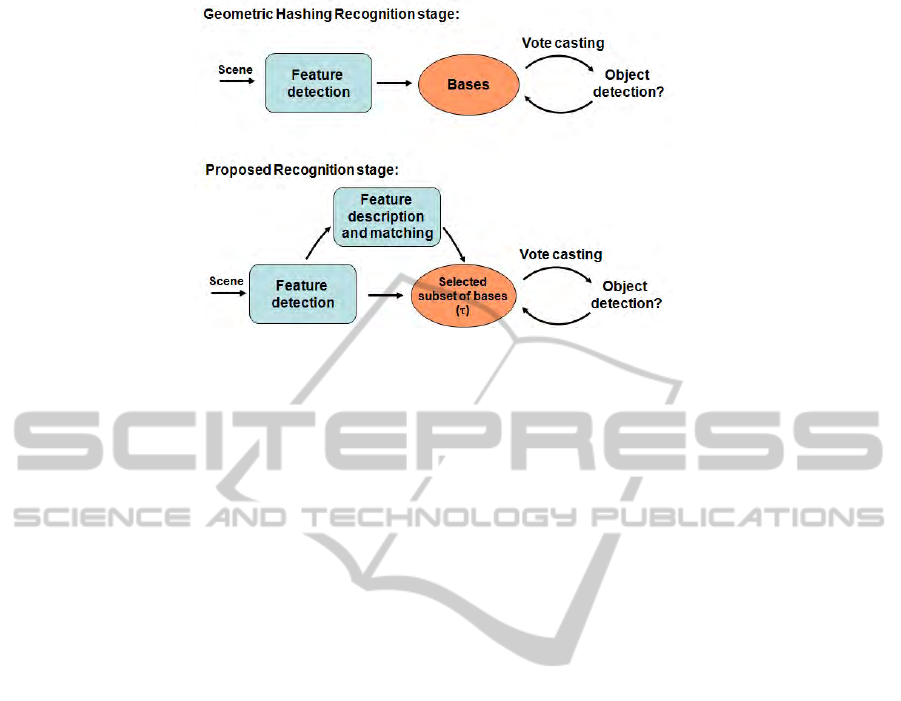
Figure 1: Recognition stage in GH and proposed method.

Several approaches have been proposed in liter-

ature to improve the basic GH formulation. (Tsai,

1996) aims at achieving higher robustness to noise

using line features instead of interest points. Yet, this

approach does not solve the problem of false positives

arising in presence of clutter and occlusions. Other

approaches aim at reducing the computational cost of

GH, e.g. by randomly select the feature points in or-

der to reduce their number (Iwamura et al., 2007) or

by limiting the matching domain to a local neighbor-

hood of a feature by means of local invariants (Iwa-

mura et al., 2007). The problem of clutter is explic-

itly handled in (Sehgal and Desai, 2003) for 3D object

recognition by incorporatinginto the object model the

information about each feature position with regards

to the object centroid. Then, at Recognition, possible

centroid positions casted by GH votes are clustered

using k-means. Drawbacks of this approach are repre-

sented by an increased computational complexity (of

the order of O(n

) plus the cost of clustering).

In this paper we propose a novel approach that

is more robust than GH to occlusion and clutter as

well as more efﬁcient when the number of features

and/or models becomes signiﬁcant. Both aspects are

in our opinion extremely important from an applica-

tion perspective, on one hand because the occlusions

and clutter are issues found in many real working

conditions, on the other because most industrial ap-

plications impose real-time or near-real-time require-

ments. In particular. the proposed approach deploys

feature descriptors to discard those features that are

prone to lead to data collisions in the hash table, thus

potentially decreasing the number of false positives in

presence of occlusions and/or clutter. This also speed-

ups the method since it notably reduces the number of

bases that need to be examined during the recognition

stage.

2 GEOMETRIC HASHING WITH

FEATURE DESCRIPTORS

In the last years, a very fertile computer vision re-

search topic has dealt with the so called invariant local

features (e.g. (Mikolajczyk et al., 2005; Mikolajczyk

and Schmid, 2005; Lowe, 2004; Bay et al., 2008)). In

such a framework, image features are detected and de-

scribed invariantly to speciﬁc set of transformations,

i.e. similarities or also afﬁnities. In particular, the de-

scription stage aims at embedding into a vector dis-

tinctive information concerning the local neighbor-

hood of the interest point for the purpose of robustly

matching features between images. Such an approach

has proved to be successful in many hard computer

vision task such as image retrieval, image registration

and stitching, camera pose estimation, 3D reconstruc-

tion and also object recognition within feature based

methods such as Hough voting and RANSAC.

In the GH algorithm, the object model is given

by the spatial information represented by the feature

locations. We aim at improving the performance of

GH by adding to this representation the distinctive

information given by the description of each feature.

More precisely, the use of this additional piece of in-

formation allows for computing correspondences be-

tween the model features and the visible (i.e. not-

occluded) object features in the target image, so as

to detect those feature points that do not match any

model feature and hence are likely to belong to clut-

ter. Accordingly, these cluttering features are not al-

lowed to form possible bases, thus rendering the over-

all algorithm signiﬁcantly less prone to possible false

positives arising by accidental accumulation of erro-

neous votes, for erroneous votes that would be casted

by feature points when evaluating such bases are in-

deed no longer casted. An additional advantageof this

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

420

approach is that, since the majority of possible basis

choices are discarded, the Recognition stage is signif-

icantly faster than with the standard GH algorithm.

We outline here the details of the proposed

method. For the sake of clarity and conciseness,

we address the case of 2D object recognition under

similarities, though the method can be generalized

straightforwardly to deal with afﬁnities as well as for

3D object recognition (Lamdan and Wolfson, 1988;

Grimson and Huttenlocher, 1990).

As sketched in Fig. 1, the ofﬂine stage is analo-

gous to that of the GH algorithm: i.e. for each model,

feature points are detected, then for each feature pair

the feature positions are transformed according to the

current basis and stored in the Hash Table. In addi-

tion, though, we also compute a descriptor for each

feature point and store it for later use. Also, we do not

consider as possible bases those feature pairs whose

distance is either too big or too small: in the former

case transformed feature coordinates would get small

values and become too prone to noise, in the latter

case the Hash Table would become too big and sparse

due to transformed feature coordinates getting large

values.

As for the online (Recognition) stage, given a

model to be sought for, ﬁrst features are detected and

described into the target image. Then, correspon-

dences between features are established by matching

each target image descriptor to the model descriptors

using as matching measure the euclidean distance. In

particular, for each target image descriptor the ratio

between the most similar model descriptor and the

second-most similar model descriptor is computed.

This nearest-neighbor search can be efﬁciently im-

plemented using efﬁcient indexing techniques such as

Kd-trees (Beis and Lowe, 1997). Once this is done for

all target image features, they are sorted in increasing

order of match conﬁdence based on this ratio: obvi-

ously, the smaller the ratio value, the higher the prob-

ability that the current feature belongs to the model.

Then, only the ﬁrst τ features are selected to form pos-

sible bases: all the other features are discarded and

won’t be considered as possible bases. The size of this

subset of features, τ, is a parameter of the algorithm:

in our experiments we have empirically selected the

value of 10. Hence the number of features used to

generate bases, n

, is given by:

= min(τ, n) (1)

Given this subset of features, S

, in turn each fea-

ture pair is selected from S

as the current basis. Also

in this case, we adopt the approach of not considering

feature pair whose distance is either too big or too

small. Once a basis is selected, all the other features

extracted (not just those belonging to S

) are trans-

formed according to the current basis and used for

casting votes as in the original GH algorithm. If votes

are accumulated in one (or more) bin of the Hash ta-

ble, then the current object is found, otherwise an-

other basis is evaluated until either the object is de-

tected or all bases have been evaluated.

It is worth pointing out that the proposed approach

can easily deal with the presence of multiple object

instances into the target image by evaluating all over-

threshold bins in the Hash Table obtained with a par-

ticular basis. As for the computational burden, it is

important to note that although our method requires

additional computations in the Recognition stage in

order to describe and match interest points, efﬁcient

algorithms do exist for both tasks (Lowe, 2004; Bay

et al., 2008)). Moreover, our method notably speeds

up the ”vote casting” process, so that the complexity

of the Recognition stage, which is O(n

) in the stan-

dard algorithm, is reduced to O(τ

n), where τ (i.e.

the number of features which are allowed to generate

bases) can easily be one order of magnitude smaller

than n. Hence, complexity is linear in the number

of features instead of cubic: this also allows for the

use of a high number of features which, as it will be

shown in the next section, helps improving the perfor-

mance of the algorithm.

3 EXPERIMENTAL RESULTS

This section presents an experimental evaluation

where the proposed approach is compared to the stan-

dard GH algorithm in an object recognition scenario.

In particular, we propose two different experiments

based on two different datasets.

3.1 Experiment 1

In Experiment 1, an object has to be recognized

within a test dataset composed of 40 images. The test

dataset is characterized by object translations, rota-

tions and -quite large- scale changes. Moreover, there

is a strong presence of clutter and occlusions. In each

of the 40 test images the object to be recognized al-

ways appears once. The object model and a few test

images are shown in Fig.2. Correct matches are de-

termined by evaluating the position error between the

ground-truth bounding box around the object and that

found by the algorithm. More speciﬁcally, we com-

pare the performance of the two algorithms by means

of Recall vs. Precision curves, by varying the thresh-

old applied on the peaks of the Hash table. To com-

pute the Recall and Precision terms, a True Positive

IMPROVING GEOMETRIC HASHING BY MEANS OF FEATURE DESCRIPTORS

421

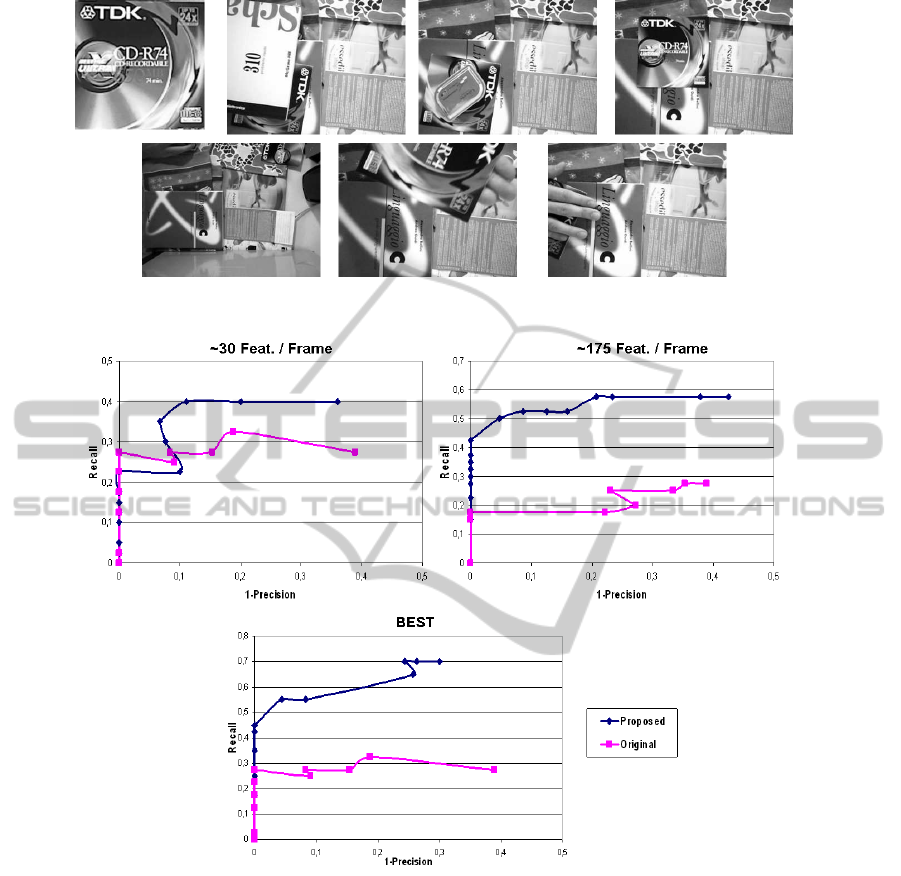
Figure 2: A subset of the dataset used in Experiment 1 (top left: the object model).

Figure 3: Experiment 1: comparison between GH and the proposed algorithm with different amounts of extracted features.

(TP) occurrs only when the 4 coordinates pairs of the

corners of the object found by the object recognition

algorithm are close enough to the ground-truth ones

(ground-truth was obtained by hand-labeling).

As for parameters, The Hash Table quantization

parameter has been tuned on the dataset, and has

the same value for both algorithms. As for the

feature descriptor, we have selected the well-known

SIFT descriptor (Lowe, 2004), which has been shown

to be discriminative and efﬁcient (Mikolajczyk and

Schmid, 2005). Interest points for both GH and the

proposed approach are extracted by means of the

DOG detector (Lowe, 2004), which is known to be

highly repeatable under several disturbance factors

such as, e.g., viewpoint changes, noise, illumination

changes, blur (Mikolajczyk et al., 2005).

We provide experimental results varying the num-

ber of extracted SIFT features. The resulting curves

are shown in Fig. 3. The left chart on top shows the

result using a small number of features - 30 on the

average per frame (the same features are extracted

and used with both methods). Instead, the right chart

on top concerns a higher number of features (175 on

the average per frame, same features for both meth-

ods). As it can be seen, the proposed approach no-

tably outperforms the original GH method in both ex-

periments, typically yielding a higher Recall at equal

(1-Precision). It is also interesting to note that the

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

422

Figure 5: Experiment 1: detection results (shown by a green bounding box) yielded by the proposed algorithm (top) and GH

(bottom) on a subset (9 images) of the evaluated dataset.

original GH method obtains better performance in

presence of a few number of features, mainly due to

the arousal of false positives when the feature num-

ber increases. On the contrary, and as expected, the

proposed method can beneﬁt of a higher number of

features since the use of a small and ﬁxed number of

”good” bases preventsfrom the malicious effect of co-

herent accumulations of erroneous votes. In addition,

the chart on the bottom shows the performance of the

two algorithms using the best number of features for

IMPROVING GEOMETRIC HASHING BY MEANS OF FEATURE DESCRIPTORS

423

Figure 4: Speed-up of proposed method over GH.

each method: as it can be seen, the proposed method

clearly outperforms the GH algorithm.

In addition, we provide indications on the efﬁ-

ciency of both algorithms by showing, in Fig. 4, the

measured speed-ups of the proposed algorithm with

regards to GH at different numbers of extracted fea-

tures: the proposed method is always faster than GH,

the speed-up increasing signiﬁcantly as n gets higher.

Finally, in Fig. 5 we provide qualitative results

concerning the detection capabilities of both algo-

rithms. More speciﬁcally, the Figure shows, by means

of a green bounding box, the output of the object de-

tection on a subset of the dataset composed of 9 im-

ages. As it can be seen from the Figure, and as it was

already indicated by the quantitative results shown in

Fig. 3, the proposed algorithm allows for a notably

more robust object detection with respect to GH in

presence of clutter and occlusions.

3.2 Experiment 2

As for Experiment 2, we deploy a larger dataset with

respect to that of Experiment 1 that is composed of

3 object models and 500 test images. This dataset

concerns an industrial application aiming at recogniz-

ing speciﬁc magazines. More speciﬁcally, 30 images

of the test dataset contain one instance of the object

models (10 images for each model), while the remain-

ing 470 images do not contain any object model in-

stance. This dataset includes the presence of rotations

and translations of the objects, in addition there is the

presence of clutter (due to the presence of other mag-

azines) and occlusions (ranging between 5−20%). A

subset of this dataset is shown in Fig. 6.

The determination of correct matches is accom-

plished exactly in the same way as in Experiment 1.

Also for this experiment, the same feature detector,

descriptor and Hash Table parameter value used for

Experiment 1 were deployed. Moreover, we use the

same parameter values of the SIFT features for both

methods so to extract the same features from each im-

age. Due to the bigger dimensions of the test images

of this dataset compared to the ones used in Experi-

ment 1, and to the fact that on the average these im-

ages are more textured, by means of the same param-

eter values used in the previous experiments we get

a much higher number of features (on the average,

∼ 1200 features are extracted from each test image).

The resulting Precision-Recall curves are shown

in Fig. 7. As it can be seen, also here the proposed ap-

proach yields notable beneﬁts in terms of recognition

accuracy compared to the original GH formulation.

4 CONCLUSIONS

We have proposed a novel method for object recog-

nition that improves the performance of the GH algo-

rithm in presence of clutter and occlusions. The use

of similarity information between features, obtained

through the use of feature descriptors, helps select-

ing a subset of good features that can reliably used in

the GH framework for object recognition in the cur-

rent scene, while ﬁltering out those creating clutter.

An additional beneﬁt brought in by the proposed ap-

proach is the much higher computational efﬁciency

when the number of interest points is high.

REFERENCES

Bay, H., Ess, A., Tuytelaars, T., and Gool, L. V. (2008).

Surf: Speeded up robust features. Computer Vision

and Image Understanding, 110(3):346–359.

Beis, J. and Lowe, D. (1997). Shape indexing using approx-

imate nearest-neighbour search in high dimensional

spaces. In Proc. CVPR, pages 1000–1006.

Chum, O. and Matas, J. (2006). Geometric hashing with

local afﬁne frames. In Proc. IEEE Conf. on Computer

Vision and Pattern Recognition, pages 879–884.

Grimson, W. and Huttenlocher, D. (1990). On the sensitiv-

ity of geometric hashing. In Proc. Int. Conf. on Com-

puter Vision, pages 334–338.

Iwamura, M., Nakai, T., and Kise, K. (2007). Improvement

of retrieval speed and required amount of memory for

geometric hashing by combining local invariants. In

Proc. BMVC2007, pages 1010–1019.

Lamdan, Y. and Wolfson, H. (1991). On the error analysis

of ’geometric hashing’. In Proc. IEEE Conf. on Com-

puter Vision and Pattern Recognition, pages 22–27.

Lamdan, Y. and Wolfson, H. J. (1988). Geometric hash-

ing: A general and efﬁcient model-based recognition

scheme. In Proc. ICCV, pages 238–249.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60:91–110.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

424

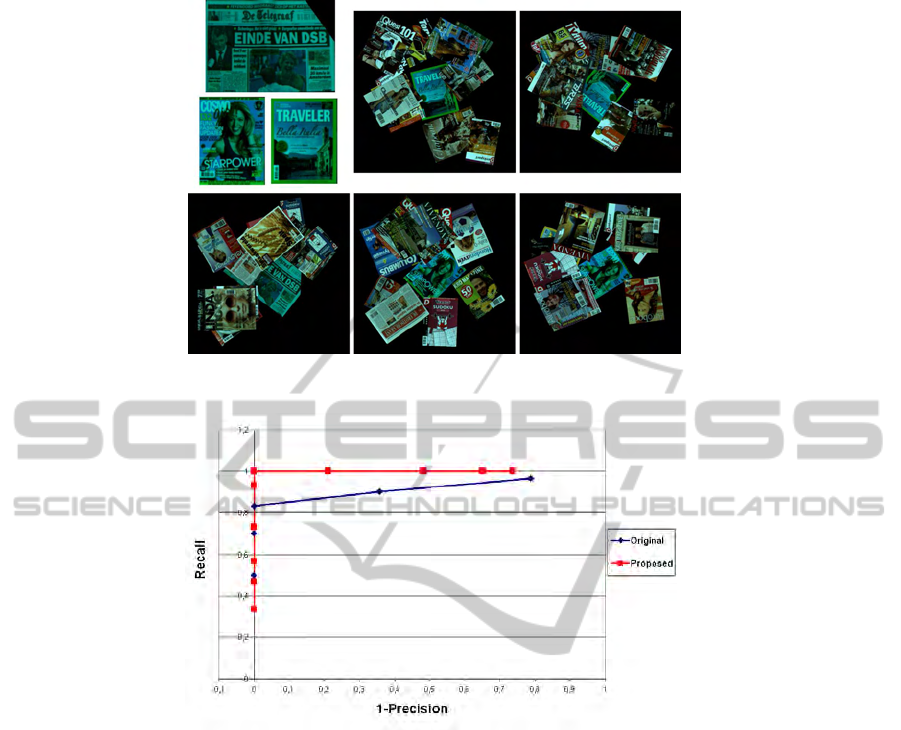
Figure 6: Dataset 2: the 3 object models (top left) and 5 examples of the test images (each one showing one instance of an

object model).

Figure 7: Comparison between GH and the proposed algorithm on the dataset of Experiment 2.

Mikolajczyk, K. and Schmid, C. (2005). A performance

evaluation of local descriptors. PAMI, 27(10):1615–

1630.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaffalitzky, F., Kadir, T., and Gool, L. V.

(2005). A comparison of afﬁne region detectors. Int.

J. Comput. Vision, 65(1-2):43–72.

Sehgal, A. and Desai, U. (2003). 3d object recognition

using bayesian geometric hashing and pose cluster-

ing*1. Pattern Recognition, 36(3):765–780.

Simon, C. and Meddah, D. (2006). Geometric hashing

method for model-based recognition of an object. US

Patent 7027651.

Tsai, F. (1996). A probabilistic approach to geometric hash-

ing using line features. Computer Vision and Image

Understanding, 63(1):182–195.

IMPROVING GEOMETRIC HASHING BY MEANS OF FEATURE DESCRIPTORS

425