
SURFACE RECONSTRUCTION FOR GENERATING DIGITAL
MODELS OF PROSTHESIS
Luiz C. M. de Aquino, Diego A. T. Q. Leite, Gilson A. Giraldi
National Laboratory for Scientific Computing, Petr
´
opolis, Brazil
Jaime S. Cardoso
INESC Porto, Faculty of Engineering, University of Porto, Porto, Portugal
Paulo Sergio S. Rodrigues
1
, Luiz A. P. Neves
2
1
FEI, S
˜
ao Bernardo do Campo, Brazil
2
Federal University of Paran
´
a, Curitiba, Brazil
Keywords:
Digital prosthesis design, Segmentation, Deformable model, Shape recovery.
Abstract:
The restoration and recovery of a defective skull can be performed through operative techniques to implant
a customized prosthesis. Recently, image processing and surface reconstruction methods have been used for
digital prosthesis design. In this paper we present a framework for prosthesis modeling. Firstly, we take the
computed tomography (CT) of the skull and perform bone segmentation by thresholding. The obtained binary
volume is processed by morphological operators, frame-by-frame, to get the inner and outer boundaries of the
bone. These curves are used to initialize a 2D deformable model that generates the prosthesis boundary in each
CT frame. In this way, we can fill the prosthesis volume which is the input for a marching cubes technique that
computes the digital model of the target geometry. In the experimental results we demonstrate the potential of
our technique and compare it with a related one.
1 INTRODUCTION
The repairing of a defective skull is needed not only
for aesthetic factors but also because large defects in
the skull may expose a significant area of the brain.
In this case cranioplasty (the procedure of repairing
holes in the skull with cranial implants) becomes nec-
essary (Sanan and Haines, 1997). In traditional sur-
gical procedures, cranioplastic implants were manu-
factured directly in the operating-theater where the
surgeon modeled by hand the material, namely poly-
methylmethacrylate (PMMA), to make the prosthe-
sis. However, the success of such procedure depends
strongly on the manual skill of the surgeon, with a
high risk of infection and a certain percentage of fail-
ure due to rejection (Solaro et al., 2008).
Nowadays cranioplasty continues to be a chal-
lenge to craniofacial surgeons which motivates the
development of computational tools for surgical plan-
ning and implants design (Chen et al., 2006; Lee et al.,
2009; Solaro et al., 2008).
In early 1980s, the introduction of 3-D CT scans
and surface reconstruction methods provided a new
effective tool for surgical planning. The generated
digital models and stereolithography rapid prototyp-
ing technologies (RP) made skull prostheses manu-
facture more accurate and customized for each case
(Lee et al., 2002).
The application of medical image processing,
computer graphics and rapid prototyping (RP) tech-
nology allows the customization of cranioplasty pro-
cedures to relieve the injury of patients in opera-
tions (Kai et al., 2009). The pipeline for the prosthe-
sis generation begins with the acquisition of the com-
puted tomography (CT) image of the skull. Then, im-
age processing methods are applied for bone segmen-
tation. Next, some surface reconstruction method is
applied to get a three-dimensional model of the pros-
thesis. Such model is the input for the next step where
the prosthesis of defective skull is manufactured us-
137
C. M. de Aquino L., A. T. Q. Leite D., A. Giraldi G., S. Cardoso J., Sergio S. Rodrigues P. and A. P. Neves L..
SURFACE RECONSTRUCTION FOR GENERATING DIGITAL MODELS OF PROSTHESIS.
DOI: 10.5220/0003356601370142
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 137-142
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ing RP technology. Lastly, the prosthesis is implanted
into the defective position.
From the viewpoint of image processing and geo-
metric modeling the approaches in this area fall into
two main categories. In the first one surface recon-
struction is usually applied to get a representation of
the defective skull which is then used to reconstruct
the digital model of the lost part. In (You et al., 2009)
we find one of such method, which divides each voxel
into tetrahedra and applies a marching technique to
get a polygonal representation of the defective skull.
Then, the method uses user-defined guiding points
and computational geometry algorithms to generate
the digital version of the prosthesis taking into ac-
count only the polygonal mesh.
The second class of techniques includes methods
that first reconstruct the skull in the image space.
Then, they apply Boolean operations and Marching
Cubes methods to get the digital model of the pros-
thesis. Reflection techniques, based on the assump-
tion of skull symmetry, belong to this class. In this
case, we can compute the axis of symmetry and re-
flect the segmented image (bone) respect to this axis.
However, this method can be used only if the lesion
do not cross that axis.
In this paper, we propose a new methodology for
digital prosthesis generation, which falls into the sec-
ond category. Our proposal is roughly divided into
5 stages: 1) Slice-by-Slice Segmentation: Extract the
bone from the other tissues; 2) Feature Extraction: get
geometric information about the frontier of the lesion
(terminal points and their tangents); 3) Deformable
Model: With the information from step 2, compute
the inner and outer boundaries of the prosthesis, using
a deformable 2D model of type balloon; 4) Prosthe-
sis Volume: Fill each patch obtained in the step above
to complete the prosthesis volume; 5) Surface Recon-
struction: Marching cubes is applied to generate the
digital version of the prosthesis geometry.
To accomplish the first step, we take each frame of
the volume and we apply a simple thresholding tech-
nique based on image inspection. Then, we perform
the feature extraction. Firstly, we use an edge detec-
tor to extract the boundary B of the bone in the binary
image and a thinning process to get the skeleton of
the bone. Then, the convex hull S is computed for the
skeleton. We consider the difference B−S as the outer
boundary of the bone and the set B ∩ S as the inner
boundary of the bone. The obtained curves are used
to get the geometric information need for the next
step. We take the end points and tangents as boundary
conditions for a deformable model, a balloon-like one
(Cohen, 1991), which is used to compute the patch
of the prosthesis in each image frame. We set two
instance of the balloon model: one to get the outer
boundary of the prosthesis and another one to get the
inner boundary of the prosthesis. In the next stage,
we recover the lost part of the bone, following the bal-
loon result in each frame. Finally, the geometry of the
prosthesis is reconstructed through a marching cubes
technique. In the experimental results we demonstrate
the advantages of our technique when compared with
the one presented in (You et al., 2009).
2 PROPOSED METHOD
The standard format for CT images is DICOM (Dig-
ital Imaging and Communications in Medicine). In
the case of CT images of the head we find the bone
as well as soft tissues (brain, skin, etc.). In a DICOM
image, the data matrix has real values in the range
[−1000,1000], called CT numbers. It is known that
the CT number for bone tissues belongs to the range
[400,1000]. So, a simple binarization method can be
performed in order to highlight just the structure of
interest. Besides, we also apply a hole filling method
to correct bone topology and a simple search process
to discard acquisition artifacts. The Figures 1.(a)-(b)
shows the original image and the segmentation result,
respectively.
(a) (b)
Figure 1: (a) Slice of the defective skull. (b) Bone segmen-
tation.
Now, once the bone is segmented, we take each
frame and get the end points of the lesion and their
tangents. In order to perform this task, we apply an
edge detector to extract the boundary B of the bone
in the binary image and a thinning process to get the
skeleton of the bone. The obtained results are pictured
on Figure 2.
Then, a convex hull S is computed for the skele-
ton. We consider the difference B − S as the outer
boundary of the bone and the set B ∩ S as the in-
ner boundary of the bone. The obtained curves are
used to get the geometric information need for the fur-
ther step. Firstly we discard a set of boundary points
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
138

Figure 2: Bone boundary and skeleton.
nearby the lost part of the bone, typically 10 points
nearby the end points of the skeleton. Then, for each
boundary, we take the boundary points inside a neigh-
borhood of each end point to fit a line which direction
will be used to get the tangent necessary for the bal-
loon model setup. This process is applied for both, the
inner and outer curves, generating the results pictured
on Figure 3.
Figure 3: (a) Inner (red) and outer (green) boundaries of the
bone plus the tangent lines.
Next, we apply a deformable model, a balloon-
like model (Cohen, 1991), to compute the patch of
the prosthesis in each image frame. We take the end
points and tangents already obtained as boundary con-
ditions for a deformable model. We set two instance
of the balloon model: one to get the outer boundary of
the prosthesis and another one to get the inner bound-
ary.
Geometrically, the balloon model (Cohen, 1991)
is described by a parametric contour c : [0,1] → D ⊂
ℜ
2
. From the dynamic viewpoint, we have a de-
formable contour which is viewed as a time-varying
curve c (s,t) = (x (s,t),y(s,t)). In this formulation,
the Lagrange equations of motion (balloon model
equation) can be expressed as:
˙c − (ω
1
c
0
)
0
+ (ω
2
c
00
)
00
=
~
F
ext
+ k~n(c), (1)
subject to c(0,t), c(1,t), c
0
(0,t), c
0
(1,t). In (1) we use
the notations ˙c ≡
∂c
∂t
, c
0
≡
∂c
∂s
, c
00
≡
∂
2
c
∂s
2
,~n(c) is the unit
normal over the curve and k is a scale factor. The field
~
F
ext
means an external force, which depends on image
elements or constraints.
In our case,
~
F
ext
= 0, each curve is an open one,
fixed in the end points of the lesion following the tan-
gents at that points. Besides these boundary condi-
tions, we must set the initial curve to complete the
initialization of each instance of the balloon.
To solve (1) we use finite differences as described
in (Cohen, 1991). In order to include the initial
curve in the numerical method, we must give an ini-
tial sequence of points C
0
= c(i∆s,0) = c
0
i
, with i =
0, ..., N, which is the discrete version of the initial
curve. Such curve must satisfies the boundary con-
ditions also. In the case of the outer curve, we can
simplify the equations by using the reference system
pictured on Figure 4, which has both the end points
on the horizontal axis (one in the origin and the other
one at x = L), to write the constraints as:
C(0) = C(L) = 0, (2)
C0(0) = tan θ
0
,
C0(L) = tan θ
1
.
Besides, the initial shape should be as closer as
possible to the target to reduce time computation. We
observe that a cubic curve, represented by
c(s) = (Ls, L(tanθ
0
+ tanθ
1
)s
3
−
L(2tan θ
0
+ tanθ
1
)s
2
+ L tan θ
0
s), (3)
where s ∈ [0, 1], fits all of these requirements.
Figure 4: Coordinate system used to setup the outer balloon.
An analogous construction can be made for the in-
ner balloon. The Figure 5.(a) shows a typical result
obtained through the deformable model. From this
result, we can complete the patch of the prosthesis in
the corresponding slice. It is just a matter of filling
the region between the obtained curves and take the
difference between this region and the bone (Figure
5.(b)). So, by executing this procedure in each slice
we can complete the prosthesis volume.
Besides, there are cases in which we observe lost
of bone without changing the topology of the corre-
sponding region. The Figure 6.(a) shows such a case.
SURFACE RECONSTRUCTION FOR GENERATING DIGITAL MODELS OF PROSTHESIS
139
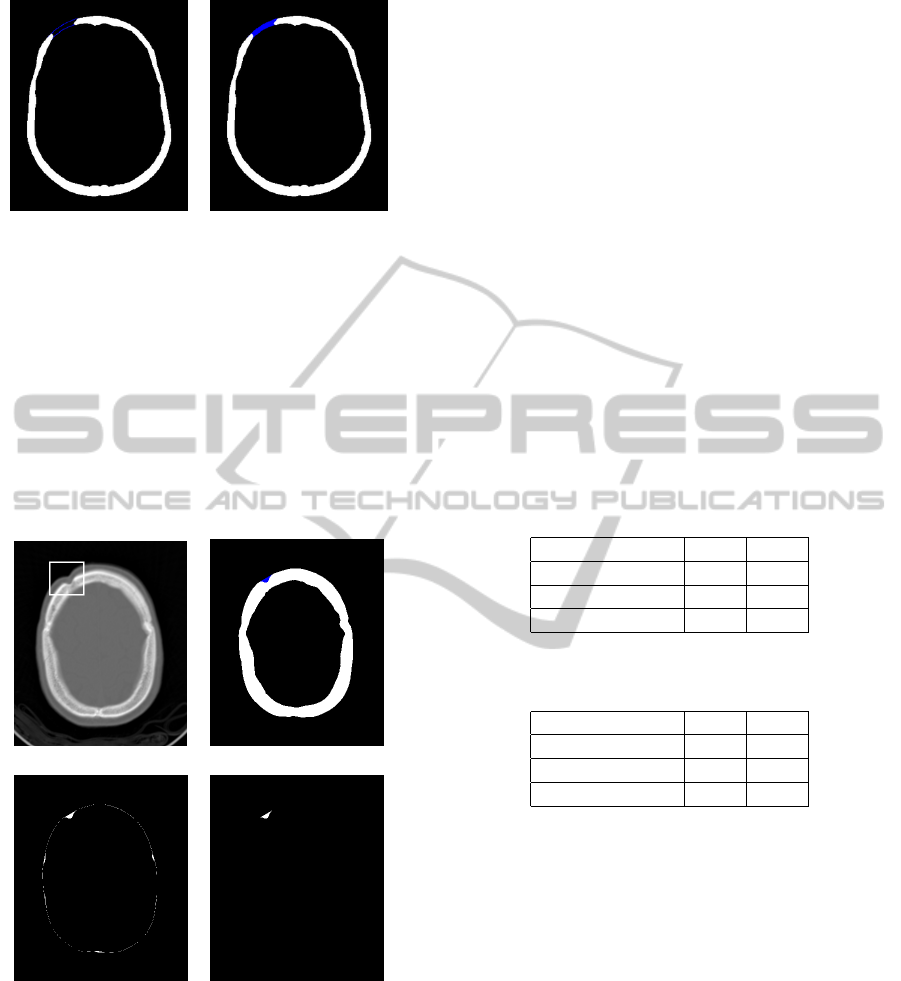
(a) (b)
Figure 5: (a) Balloon results. (b) Prosthesis patch (in blue).
The bone region, pictured in white on Figure 6.(b),
has a skeleton given by a closed curve which automat-
ically indicates this problem. In this case, we can as-
sume that the lost region is small. Therefore, we just
take the difference between the segmented bone and
its convex hull (Figure 6.(c)). Then we discard small
islands and the biggest region to isolate the prosthe-
sis patch, pictured on Figure 6.(d). In the final stages,
we recover the geometry of the prosthesis through a
marching cubes technique.
(a) (b)
(c) (d)
Figure 6: (a) Original slice with defective region high-
lighted. (b) Segmented bone. (c) Difference between the
convex hull and the bone region. (d) Prosthesis patch.
3 EXPERIMENTAL RESULTS
The proposed model is applied to generate the pros-
thesis for repairing the defective skull pictured on Fig-
ure 8.(a). In this case, we can also use a reflection
technique, based on the assumption of skull symme-
try, to reconstruct the skull. We will use this solution
to measure the quality of the result. The defective re-
gion intersects 23 slices of the whole image volume
(68 slices). Three of them are processed using the
convex hull, like in Figure 6 and the other ones are
processed through the balloon model.
In the experiments of this section we set null the
external force in expression (1). Following (Cohen,
1991), the parameters ω
0
and ω
1
are set to (∆s)
2
and (∆s)
4
, for both the balloon instances where ∆s
is the discretization step applied to get the numeri-
cal solution of equation (1). The value of the normal
force scale parameter is k = −0.062. The stopping
criterium for the iterative method used to solve (1)
is based on expression
C
t+∆t
−C
t
≤ 10
−3
, where
C
t+∆t
and C
t
are the curves at time t + ∆t and t. The
Tables 1 and 2 report some statistics about the initial-
ization (expression (3)) and evolution of the balloon
instances.
Table 1: Outer balloon: Statistics for parameters (θ
0
, θ
1
)
and number of interactions of balloon.
Parameter Min Max
θ
0
4
◦
22
◦
θ
1
156
◦
169
◦
No. Interactions 48 135
Table 2: Inner balloon: Statistics for parameters (θ
0
, θ
1
)
and number of interactions of balloon.
Parameter Min Max
θ
0
12
◦
29
◦
θ
1
143
◦
156
◦
No. Interactions 31 147
Considering that the mean number of interactions
of the numerical scheme is 135 for the outer balloon
and 147 for the inner one and we have a mean num-
ber of 21 snaxels for the balloon model instance, we
can say that the computational cost is not expensive.
The Figures 7.(a)-(c) show three slices and the cor-
responding prosthesis patches. In the first two cases,
the result is visually acceptable. However, the Fig-
ure 7.(c) shows that the thickness of the prosthesis
patch is not suitable in this case, as we can observe
with a zoom in the defective region, pictured on Fig-
ure 7.(d). This problem happens because we did not
get the suitable boundary conditions. We will address
this problem in further works.
Figures 8.(b)-(d) show three viewpoints of the re-
paired skull. A visual inspection indicates that the
prosthesis geometry suitably reconstructs the defec-
tive region. However, the method is sensitive to the
parameters choice. So, we must be careful about this
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
140

(a) (b)
(c) (d)
Figure 7: (a)-(c) Prosthesis patches obtained with our
method. (d) Zoom in the patch of last figure.
(a) (b)
(c) (d)
Figure 8: (a) Original defective skull. (b)-(d) Skull surface
reconstructed.
point during the setup of the balloon technique.
In order to measure the quality of the obtained
result we compute a similarity measure, based on
the distance from the top and inner surfaces of the
prosthesis and the prosthesis generated by reflection,
taken as a ground truth. Specifically, for each node of
the top (inner) surface we calculate the distance from
the corresponding surface obtained by reflection. The
Table 3 reports a statistics for the distance field ob-
tained. For the top surface the reported minimum dis-
tance is 0.0 and the maximum one is 2.89.
Therefore, the distance field lies in the range
[0,2.89], which is acceptable if we consider that the
Table 3: Statistics for the distance field (in voxel units) be-
tween the prosthesis surfaces and the ground through (re-
flection).
Distance Top Inner You et al.
Min. 0.0 0.0 0.06
Max. 2.89 3.16 6.06
Mean 1.10 0.72 3.09
StD. 0.52 0.48 1.34
resolution of the skull volume is 512 × 512 × 68 vox-
els. The inner surface precision is smaller; between
[0,3.16]. However, the Figure 9 shows that the maxi-
mum distance happens in small places over the pros-
thesis surface. This figure shows a color map that pic-
tures the intensity of distance field. This fact is also
confirmed through the standard deviation (named StD
in Table 3), which is too smaller then the maximum
distance.
(a) (b)
(c)
Figure 9: (a) Distance map plotted over the top surface ob-
tained by our method. (b) Artificial inner surface and col-
ored distance map. (c) Top surface and distance map for
You et al. technique.
It is worthwhile to compare our method with the
one proposed by You et al. in the reference (You et al.,
2009). The Figure 10 pictures the solution obtained
with that method. It does not take into account the
tangent directions at the boundary of the hole. There-
fore, the obtained prosthesis may not fit the curvature
of the skull. In fact, the method has a bias towards
planar shapes due to the fact that there is no any con-
straint related to local curvature. We can check this
problem in the result pictured on Figure 10 as well
as through comparisons with the reflection result pre-
SURFACE RECONSTRUCTION FOR GENERATING DIGITAL MODELS OF PROSTHESIS
141

sented on the third column of Table 3, for the top sur-
face. All the reported distances are higher than the
ones reported by our technique which indicates that
we can better recover the curvature of the region. This
fact is also confirmed by the distance field pictured on
Figure 9.(c).
(a) (b)
Figure 10: (a) Viewpoints of the solution obtained by the
method described in (You et al., 2009). (b) A viewpoint of
the prosthesis generated by our technique.
4 CONCLUSIONS AND FUTURE
WORKS
Based on a deformable model, a method is proposed
to reconstruct the defective position of a skull. The
goal is to construct the prosthesis model for the defec-
tive region. We show a promising result and compare
our technique with a state-of-the-art one, showing that
our method can generate a more suitable prosthesis
geometry.
Future directions for our work are to improve the
method that obtain the boundary conditions (avoid-
ing the problem pictured on Figure 7). We also plan
to test and compare the approach with other available
techniques (Hu et al., 2007; Lin et al., 2008). Besides,
we intend to apply a 3D deformable model, using D-
NURBS (Qin and Terzopoulos, 1996), to get the pros-
thesis geometry. It could address the staircase defect
generated by the slice-by-slice strategy and generate
more smooth patches.
ACKNOWLEDGEMENTS
Authors would like to thank the support provided by
CNPq, CAPES (grant 094/2007) and FAPERJ (grant
E-26/170.030/2008).
REFERENCES
Chen, J.-J., Liu, W., Li, M.-Z., and Wang, C.-T. (2006).
Digital manufacture of titanium prosthesis for cranio-
plasty. The International Journal of Advanced Manu-
facturing Technology, 27(11-12):1148–1152.
Cohen, L. D. (1991). On active contour models and bal-
loons. CVGIP:Image Understanding, 53(2):211–218.
Hu, Q., Yang, H., and Yao, Y. (2007). A software method to
model and fabricate the defective bone repair bioscaf-
fold using in tissue engineering. In Li, K., Li, X.,
Irwin, G., and He, G., editors, Life System Model-
ing and Simulation, volume 4689 of Lecture Notes in
Computer Science, pages 445–452. Springer Berlin /
Heidelberg.
Kai, C. C., Meng, C. S., Ching, L. S., Hoe, E. K., and
Fah, L. K. (2009). Cranioplasty using polymethyl
methacrylate prostheses. Journal of Clinical Neuro-
science, 16(1):56–63.
Lee, M.-Y., Chang, C.-C., Lin, C.-C., Lo, L.-J., and Chen,
Y.-R. (2002). Custom implant design for patients with
cranial defects. Engineering in Medicine and Biology
Magazine, IEEE, 21(2):38–44.
Lee, S.-C., Wu, C.-T., Lee, S.-T., and Chen, P.-J. (2009).
Cranioplasty using polymethyl methacrylate prosthe-
ses. Journal of Clinical Neuroscience, 16(1):56–63.
Lin, L., Zhang, J., and Fang, M. (2008). Modelling the bio-
scaffold for repairing symmetrical and unsymmetrical
defective skull. In Bioinformatics and Biomedical En-
gineering, 2008. ICBBE 2008. The 2nd International
Conference on, pages 905–908.
Qin, H. and Terzopoulos, D. (1996). D-nurbs: a physics-
based framework for geometric design. Visualiza-
tion and Computer Graphics, IEEE Transactions on,
2(1):85 –96.
Sanan, A. M. and Haines, S. J. M. (1997). Repairing holes
in the head: A history of cranioplasty. Neurosurgery,
40(3):588–603.
Solaro, P., Pierangeli, E., Pizzoni, C., Boffi, P., Scalese,
G., Di Lorenzo, N., and Pirillo, V. (2008). From
computerized tomography data processing to rapid
manufacturing of custom-made prostheses for cran-
ioplasty: Case report. Journal of Neurosurgical Sci-
ences, 52(4):113–116.
You, F., Hu, Q., Yao, Y., and Lu, Q. (2009). A new modeling
method on skull defect repair. Measuring Technology
and Mechatronics Automation, 2009. ICMTMA ’09.
International Conference on, 1(11-12):568–572.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
142
