VIEWPOINT SELECTION BY PAINTING

akashi Michikawa, Hiromasa Suzuki

RCAST, The University of Tokyo, Meguro, Tokyo, Japan

Ken-ichi Anjyo

OLM Digital, Setagaya, Tokyo, Japan

Keywords:

Viewpoint selection, Painting, Depth buffer.

Abstract:

Complex 3D models are very time-consuming to render, and it is difﬁcult to achieve the desired viewpoint

for them using interactive methods such as virtual trackballs. This paper presents an intuitive method for

computing good camera positions through a simple painting interface. Given a 3D scene, the user simply

paints the region of interest (ROI) on the 2D screen, and the camera is repositioned to pan in on it. Since the

computation uses depth buffers, it is independent of the complexity of the model; this makes it efﬁcient for

viewing complicated 3D models. Here, we also demonstrate several applications in 3D painting, sketching

and light placement.

1 INTRODUCTION

Manipulating 3D models to the desired position is

a fundamental task in computer graphics, computer-

aided design and other related ﬁelds. However, it is

hard to apply direct 3D operations such as painting

and sketching to models in their initial position. Ac-

cordingly, the user controls the camera position using

a virtual trackball (VT) (Chen et al., 1988; Shoemake,

1992) to pan in on the desired region. In this study, we

focus on view navigation techniques for massive 3D

models.

Our motivation comes from the visualization and

manipulation of massive scanned models. Recent

progress in scanning technology enables us to obtain

point sets with high resolution, and various commu-

nities now utilize scanned data for the preservation of

cultural assets and in digital engineering. In these ap-

plications, massive point sets are obtained from sur-

face scanners and converted to polygonal models by

surface reconstruction algorithms. The size of such

polygonalmodels easily exceeds ten million triangles.

A number of issues related to virtual trackballs

come to light when we combine them with massive

models. Suppose ten million triangles are examined

using a virtual trackball; there are gaps between the

user’s action and the display results because this is an

interactive process and the object must be rendered

for each frame. Massive models cannot maintain an

efﬁcient FPS rate even if a high-end GPU is used.

Although this problem is preventable by using low-

resolution models, the user needs to perform many

operations to reach the desired point, because a vir-

tual trackball provides only rotation operation, and is

independent of translation and scaling.

We present a geometry-driven camera placement

technique that uses a painting interface. The method

simply involvesthe user painting the region of interest

(ROI). An algorithm then reconstructs the camera po-

sition based on this region to pan in on it. Technically

speaking, the technique estimates ray direction as a

normal vector of the ROI and reconstructs the camera

position so that the view volume covers the region.

One of the key points of our method is computa-

tion using depth buffers of 2D images. The technique

requires mask images of the ROI and the depth buffer

of the scene. This provides various beneﬁts as fol-

lows:

• It is independent of model complexity.

• Various geometric types are handled.

• The power of graphics APIs can be leveraged.

A painting-based interface also provides a more

global and precise way to specify the ROI than con-

ventional GUIs. If an area is speciﬁed by picking in-

dividual elements, too many faces or vertices must be

296

Michikawa T., Suzuki H. and Anjyo K..

VIEWPOINT SELECTION BY PAINTING.

DOI: 10.5220/0003360802960301

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 296-301

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

selected to deﬁne the ROI. On the other hand, if it

is speciﬁed by drawing a rectangle, unnecessary re-

gions are also selected, which affects the results. A

painting interface resolves these problems; by paint-

ing, the user can select many elements at once and

choose only the desired region.

Moreover, our method can be used not only for

camera placement but also for other purposes. In

this work, we additionally present a number of appli-

cations to 3D painting/sketching and decal and light

placement.

2 RELATED WORK

2.1 Viewpoint Selection

Ways of achieving the desired camera position have

been studied for model recognition and creating

thumbnails. Most such methods are based on solv-

ing minimization or maximization problems. (Ka-

mada and Kawai, 1988) ﬁrst studied this issue by min-

imizing the number of degenerated faces under or-

thogonal projections. (Lee et al., 2005) maximizes

view saliency, or feature points, while (Podolak et al.,

2006) maximizes as many symmetry features as pos-

sible. (Fu et al., 2008) proposed a method for ﬁnd-

ing a stable from symmetry and supporting planes by

convex hull. (Bordoloi and Shen, 2005; Takahashi

et al., 2005) proposed methods for ﬁnding viewpoints

for volumetric models. These methods involve auto-

matic operations, but only compute viewpoints so that

the whole object is ﬁtted into the window; they cannot

focus on parts of objects without user interaction.

2.2 Directable Viewpoint Selection

The use of haptic devices provides an intuitive way

to manipulate objects. For instance, the ArtNova sys-

tem(Foskey et al., 2002) introduces a viewpoint navi-

gation system similar to that of our approach, in that

it allows the user to select the desired point. However,

this method allows only a single point to be chosen;

our system is more general, and does not require spe-

cial devices.

The HoverCam(Khan et al., 2005) provides a

method for interactive navigation with proxy(simple)

objects so that surfaces come to the front of the view-

point. In addition, multiscale navigation is also en-

abled by managing proxies by hierarchical data struc-

ture. However, this assumes original or proxy sur-

faces are relatively smooth or it is weak with noisy

models. More recently, (McCrae et al., 2009) ex-

tended this to image-based methods which enable not

(a) 3D view (b) Depth buffer

(e) Updated 3D view

Figure 1: An overview of our algorithm.

only view navigation but also collision detection on

GPUs and achieved multi-scale navigation of very

large scenes. These methods are also close to ours,

however their purpose is different. Our method is

designed for viewing and manipulating unstructured

massive scanned models with low FPS.

(Hachet et al., 2008) proposed an excellent in-

terface to select viewpoints. Given a point or circle

strokes as a region by the users, it gives a 3D widget

in the region to control an optimal view. However,

this is difﬁcult to ﬁnd an optimal viewpoint from cur-

rent view. Although they provide a preview window

to help it, they need to render scenes and it may take

time for massive models.

3 ALGORITHM

The our method interface is quite simple; users simply

paint the region they want to see. Fig. 1 shows an

overview of the algorithm used.

Given a 3D scene (a), the depth buffer (b) is ﬁrst

captured from the scene. The results of the painting

are stored as a mask image (c), and the depth buffer is

then clipped using this image (d). The region of inter-

est or point set P = {p

} is computed by the clipped

depth buffer. Our algorithm computes camera infor-

mation C from P and the current camera information

C(e). According to (Blinn, 1988), C includes follow-

VIEWPOINT SELECTION BY PAINTING

297

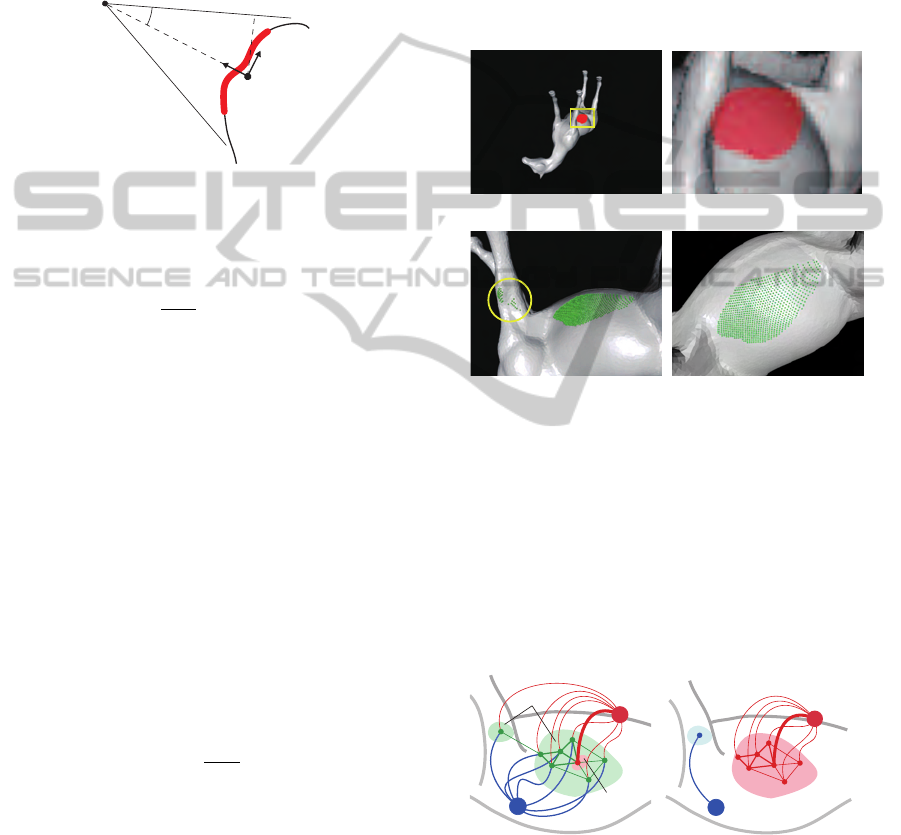
ing components (Fig. 2):

• e : eye position

• c : center of interest

• u : up vector

• θ : the perspective angle of the camera. In this

paper, we assume that remains unchanged.

Here, we introduce the method of computation.

ROI

Figure 2: Camera information.

The center of interest is given by taking the

weighted center of mass of P as shown in Eq.1,

c =

∑

∈P

, (1)

where w

denotes the area around p

. The reason for

introducing w

is that corresponding points in 3D are

sampled non-uniformly.

Next, we ascertain the ray vector n for computing

e. It is natural that n is the normal vector of a tangent

plane of P. Here, we use a method for estimating the

normal vector of a point set (Hoppe et al., 1992). We

construct a co-variance matrix M of P in Eq. 2,

M =

∑

∈P

− c)

− c). (

We use n as the eigenvectorcorresponding to the min-

imum eigenvalue of M. Then, the direction of n satis-

ﬁes (n,

n) > 0, where

n denotes the normal vector of

the current scene.

The eye point e can then be reconstructed from c

and n using Eq. 3,

e = c+

sinθ

n, (3)

where R and θ denote the radius of bounding sphere of

P and the ﬁeld of view angle in the current perspective

view, respectively (Fig. 2).

By using n and

n, we can obtain a rotation matrix

R such that n = R

n. The up vector u is computed by

R using Eq. 4,

u = R

u. (4)

Finally, the camera position is updated by the

graphics API (e.g., gluLookAt()).

3.1 Outlier Removal

Our algorithm is weak with irregular points (outliers)

(shown in the yellow circle in Fig. 3(c)) caused by

mispainting (Fig. 3(a) and (b)) or scanning noises

because they affect the covariance matrix in Eq. 2,

and invalid ray vectors are computed (Fig. 3(c)). Of

course, such points can be removed by erasing the

paint, but we introduce an automatic removal method

using global optimization solutions such as graph-cut

(Boykov and Kolmogorov, 2004).

(a) Over-painting (b) Close-up view of (a)

Figure 3: Outlier removal by graph-cut segmentation. The

green spheres are 3D points unprojected from depth buffers.

The graph-cut algorithm is a minimum-cut algo-

rithm for graphs (Fig. 4), and is widely used in im-

age processing problems. We use it to automatically

remove outliers caused by mispainting (Fig.3 (c)).

However, cost assignment is a difﬁcult task. Here,

we discuss a strategy to assign costs between nodes

for graph-cut application.

Sink node

Source node

(a) Cost setting

Outlier

Correct ROI

(b) Minimum cut

Figure 4: Graph cut segmentation in outlier removal.

From observation of Fig. 3 , we can draw the follow-

ing assumptions:

1. The mispainted region is relatively small, and cre-

ates small clusters (Fig. 4(a)).

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

298

2. The depth value of the mispainted region is sig-

niﬁcantly different from that of the correct region.

From assumption 1, we can extract a point set F =

} that must belong to the correct ROI (Fig. 4

(a)). These can be obtained by taking the k-th nearest

points from the median of the depth buffers in P. The

other points U = {u

} are considered as unknown.

Now we assign a weight to each edge between v

and

source/sink nodes as shown in Eq. 5,

w(v

, S) =



∞ v

∈ F

1 v

∈ U

w(v

, T) =



0 v

∈ F

α v

∈ U

, (5)

where S and T are the roots of the source and sink

nodes respectively. α is a parameter to control the

results.

Next, we assign a weight to each edge between

neighboring nodes v

and v

based on assumption 2.

If two nodes are close to each other, they are hard to

cut and their cost must be low and vice versa. The

cost function between nodes is given by Eq. 6.

E(v

, v

) =

||v

− v

, (6)

where β is a user-given parameter.

Fig. 3 shows an example. Here, the user intends

to paint the body of the horse model. We apply graph-

cut in the preprocessing phase to remove such noise

before the viewpoint computation phase. It is seen

that the expected results can be computed as a result

of outlier removal from Figure 3(d). In this case, α =

10 and β = diag(P) : diagonal length of the bounding

box of P used.

4 RESULTS AND DISCUSSION

4.1 Implementation

We implemented a prototype system with OpenGL

and GLUT. Note that this algorithm can be imple-

mented without any special functions. For instance,

glReadPixels() is used to capture depth buffers, and

gluUnproject() is used to compute 3D points from

depth values. This means the algorithm does not re-

quire expensive GPUs.

4.2 Results

Figs. 1, 5, 6 and 7 show several results obtained using

our method. In each ﬁgure, (a) shows the input cam-

era position with the ROI drawn in red, and (b) shows

the reconstruction resulting from this technique.

(a) (b)

Figure 5: Results for scanned objects(120,303 triangles).

(a) (b)

Figure 6: Results for a scanned point set (1,282,225 points).

4.3 Discussion

Figs. 1, 5, 6 and 7 demonstrate results for point sets

and polygons. These ﬁgures show that our method

can be applied to various types of geometric mod-

els. This is because geometry is captured from depth

buffers, and intersections between rays and objects

are not considered.

Our method retrieves geometry from depth

buffers, and does not render during the navigation

phase. This means that there are not gaps between

user action and display results even with massive

models. Fig. 7 shows a model of David with over ten

million triangles. With such complex models, it usu-

ally takes a long time to reach the desired position.

However, our method achieves appropriate position

with a single user action.

(a) (b)

Figure 7: Results for complex models(11,169,874 trian-

gles).

Fig. 8 shows computational statistics for ﬁnding

viewpoint described in Section 3. All examples are

measured in the following environments :

• 32 bit : Intel Core 2 Duo 2.13GHz + GeForce

7300GS (521MB)

VIEWPOINT SELECTION BY PAINTING

299

• 64 bit : Intel Xeon 3.16GHz + QuadroFX 1700

(512MB)

Note that the David model cannot be rendered on a

32-bit OS due to memory allocation error. We can see

computation time for each example is almost same,

although the number of elements is different. On the

other hand, the size of the frame buffer affects per-

formance because it takes much time to retrieve the

depth buffer.

0.5

1.5

2.5

3.5

640x480 1024x768 1280x1024

Computation time (sec.)

Resolution of frame buer

Elephant

CAD mesh

Horse

Elephant(x64)

CAD mesh(x64)

Horse(x64)

David(x64)

Figure 8: Statistics.

One of advantages of paint-based interface is to

specify complex ROIs as shown in Fig. 9. In this ex-

ample, we paint four soles of the horse model(a), and

our method computes the viewpoint so that we can see

them at once(b). Note that other methods(rectangle

and cursor) cannot work well. This is because they

capture unnecessary region, and invalid viewpoint

will then be computed.

(a) Paint (b) Result

Figure 9: Focus on multiple ROIs.

The quality of C depends on that of the depth

buffer. If the near and far clipping planes are far from

each other, the precision of the depth value is worse

when the surface is close to the far clipping plane

Accordingly, we need to consider clipping plane man-

agement to ensure a tight ﬁt to the model. This can be

resolved by ﬁnding min/max depth values and using

them as clipping planes.

http://www.opengl.org/resources/faq/technical/

depthbuffer.htm

5 APPLICATIONS

5.1 3D Painting and Sketching

Direct painting and sketching onto 3D surfaces is an

intuitive method for the modeling process. Accord-

ingly, it is better for capturing and focusing on sur-

faces on which users paint or sketch. Fig. 10 shows a

framework of 3D painting with our method interface

implemented in Autodesk Maya. A good viewpoint

for 3D painting can be obtained through this method

with a single user action, thus accelerating the paint-

ing process.

(a) Painting (b) Updated viewpoint

Figure 10: Framework of 3D painting with our method.

This technique can be used not only for painting

and sketching but also for decal arrangement. Since

decal placement uses projection mapping, it is difﬁ-

cult to achieve the desired direction when mapping

decals onto curved or bumpy surfaces. Fig. 11 shows

an example of decal arrangement in Maya. Here, we

map a decal texture (a) onto the left eye of a horse

model (b). our method is used to compute the projec-

tion plane.

(a) Decal (512x512)

(b) Mapping (c) Result

Figure 11: Example of decal arrangement with our method.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

300

5.2 Light Placement

Our algorithm can also position lights appropriately

(Fig. 12). The interface is almost the same as that for

camera placement. The user paints the region where

the light is needed, and the algorithm creates a spot-

light to illuminate the area speciﬁed. The light posi-

tion, the direction and cut-off ratio for the spot light

correspond to the e, n and θ in Section 3 respectively.

This is efﬁcient for CG animations. In CG production,

there is often a need to place lights in an eccentric po-

sition to obtain plausible shading.

(a) Painting ROI (b) Lighting result

Figure 12: Light placement by painting.

6 CONCLUSIONS

We have presented a painting interface for camera

placement. Our algorithm requires only speciﬁcation

of the region of interest by painting, and the cam-

era is then repositioned based on the ROI. We remark

that our method is not the alternative of other existing

methods, and we suppose to use the proposed method

with them. For instance, we use our method for ﬁnd-

ing intial viewpoint and we adjust the viewpoint by

other methods(e.g. zoom out).

We also have plans for related future work. First,

the good up vector need to be computed. Second, we

would like to extend this method to volumetric mod-

els or we would like to ﬁnd a viewpoint by direct

painting on volume rendering display.

ACKNOWLEDGEMENTS

Models are cortesy of Georgia Tech(Fig.1),

AIM@shape(Fig. 6) and Stanford Digital Michelan-

gelo Project (Fig. 7). This work is partially suppoted

by KAKENHI (No. 22246018, No. 22700091).

REFERENCES

Blinn, J. (1988). Where Am I? What Am I Looking At?

IEEE CG&A, 8(4):76–81.

Bordoloi, U. D. and Shen, H.-W. (2005). View selection for

volume rendering. IEEE Visualization, 0:487–494.

Boykov, Y. and Kolmogorov, V. (2004). An experimental

comparison of min-cut/max-ﬂow algorithms for en-

ergy minimization in vision. IEEE PAMI, 26(9):1124–

1137.

Chen, M., Mountford, S. J., and Sellen, A. (1988). A study

in interactive 3-d rotation using 2-d control devices.

In SIGGRAPH ’88, pages 121–129.

Foskey, M., Otaduy, M. A., and Lin, M. C. (2002). Artnova:

Touch-enabled 3d model design. In IEEE Virtual Re-

ality, page 119.

Fu, H., Cohen-Or, D., Dror, G., and Sheffer, A. (2008). Up-

right orientation of man-made objects. ACM Transac-

tions on Graphics, 27:42:1–42:7.

Hachet, M., Decle, F., Kn¨odel, S., and Guitton, P. (2008).

Navidget for easy 3d camera positioning from 2d in-

puts. In Proceedings of IEEE 3DUI, pages 83–88.

Hoppe, H., DeRose, T., Duchamp, T., McDonald, J., and

Stuetzle, W. (1992). Surface reconstruction from un-

organized points. In SIGGRAPH ’92, pages 71–78.

Kamada, T. and Kawai, S. (1988). A simple method

for computing general position in displaying three-

dimensional objects. Comput. Vision Graph. Image

Process., 41(1):43–56.

Khan, A., Komalo, B., Stam, J., Fitzmaurice, G., and

Kurtenbach, G. (2005). Hovercam: interactive 3d nav-

igation for proximal object inspection. In I3D ’05,

pages 73–80, New York, NY, USA. ACM.

Lee, C. H., Varshney, A., and Jacobs, D. W. (2005). Mesh

saliency. In ACM SIGGRAPH 2005 Papers, pages

659–666.

McCrae, J., Mordatch, I., Glueck, M., and Khan, A. (2009).

Multiscale 3d navigation. In I3D ’09, pages 7–14,

New York, NY, USA. ACM.

Podolak, J., Shilane, P., Golovinskiy, A., Rusinkiewicz, S.,

and Funkhouser, T. (2006). A planar-reﬂective sym-

metry transform for 3d shapes. In ACM SIGGRAPH

2006 Papers, pages 549–559.

Shoemake, K. (1992). Arcball: a user interface for speci-

fying three-dimensional orientation using a mouse. In

Graphics interface ’92, pages 151–156.

Takahashi, S., Fujishiro, I., Takeshima, Y., and Nishita, T.

(2005). A feature-driven approach to locating optimal

viewpoints for volume visualization. IEEE Visualiza-

tion, 0:495–502.

VIEWPOINT SELECTION BY PAINTING

301