ANALYSIS OF DETERMINISTIC END-TO-END DELAY
IN MULTI-HOP AFDX AVIONICS NETWORK SYSTEM
∗
Xiaoqiang Ji
∗
, Huanzhong Li
†
, Jian Li
∗
, Hairui Zhou
∗
, Fei Hu
∗
, Xue Liu
‡
and Guchuan Zhu
§
∗
School of Software, Shanghai Jiao Tong University, Shanghai, China
†
School of Computer Science, McGill University, Montreal, Canada
‡
Department of Computer Science & Engineering, University of Nebraska Lincoln, Lincoln, U.S.A.
§
Department of Electrical Engineering,
´
Ecole Polytechnique Montr´eal, Montreal, Canada
K
eywords:
AFDX, Network calculus, Arrival curve, Service curve, Pay burst only once, Delay bound.
Abstract:
Avionics Full Duplex Switched Ethernet (AFDX) is a deterministic communication protocol for real-time
applications on Ethernet media. It is a promising technique that can improve the interconnection of electronic
devices in an aircraft. One of the key challenges in employing AFDX is to determine the transmission delay
in such a network. This paper aims at handling this challenge by theoretical analysis. A network calculus-
based approach is presented for analyzing the end-to-end transmission delay of virtual links in an AFDX
network that may consist of many network nodes with different scheduling disciplines. We further improve
the approach by taking the specific effects of virtual links into account. In addition, we conduct a simulation to
verify the validity of our approach. Simulation results show that switches with different scheduling disciplines
can improve the delay performance in a multi-hop network.
1 INTRODUCTION
Avionics Full Duplex Switched Ethernet (AFDX) is
an avionics data bus system emerging in recent years.
AFDX standard provides a detailed description of
the electrical requirements and protocol specification
(ARINC, 2005). With bandwidth up to 100Mbps,
AFDX network is a thousand times faster than its pre-
decessor - ARINC429. With a continuously increas-
ing number of a variety of devices and amount of data
traffic, ARINC429 has gradually failed to meet the re-
quirements of modern avionics systems. Thanks to its
low cost, high speed, good scalability and other tech-
nical advantages, AFDX will become one of the fu-
ture mainstream technologies to replace the existing
avionics data buses, such as ARINC429, MIL-STD-
1553B and so on.
In the actual deployment, the important issue is
the calculation of the end-to-end transmission delay
in an AFDX network. Ensuring a bounded transmis-
sion delay is essential to a hard real-time system such
as the avionics system. One of the key challenges
in assessing deterministic real-time guarantees and
∗
This work was supported by NSFC 61003011 and
MOST 2010DFA11390.
bounded delay in data transmission is how to calcu-
late the end-to-end delay effectively and accurately.
There are many methods for calculating the net-
work transmission delay, for example, network sim-
ulation, network calculus, model checking technique,
etc (Charara et al., 2006). Nowadays, due to the ad-
vantage of applicability and rigour, network calculus
theory is often used for analyzing the real-time per-
formance of communication networks, especially in
the worst-case transmission delay analysis.
In previous works, the scenario that a number of
virtual links pass through several switches with dif-
ferent scheduling algorithms is not involved, so the
method for computing the end-to-end delays is not
given to handle this scenario effectively. In this pa-
per, we propose a novel framework to analyze the
end-to-end transmission delay in a multi-hop AFDX
network using network calculus. Based on the service
curve model and delay analysis theorems of network
calculus, an upper bound on the end-to-end delay
is computed. Our network calculus-based approach
can analyze most virtual links in an AFDX network
that consists of different network nodes with common
scheduling disciplines.
The main contributions of our research are sum-
434
Ji X., Li J., Li H., Zhou H. and Hu F..
ANALYSIS OF DETERMINISTIC END-TO-END DELAY IN MULTI-HOP AFDX AVIONICS NETWORK SYSTEM.
DOI: 10.5220/0003361204340440
In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2011), pages
434-440
ISBN: 978-989-8425-48-5
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

marized as follows. We present models of AFDX
nodes (End System and AFDX Switch), and calculate
service curves of various scheduling disciplines that
can be used in AFDX nodes. Using the “pay burst
only once” phenomenon and service guarantee theo-
rem of network calculus, we acquire an analytical up-
per bound on the end-to-end delay of a virtual link by
computing the maximum horizontal distance between
service curve and arrival curve. Note that we do not
use the sum of all node delays as the end-to-end delay
of a virtual link, because of the repetitive delay calcu-
lations in a multi-hop network. Taking the effects of
virtual links that share a common physical link into
account, we further improve the delay bound by opti-
mizing the delay calculation in the FCFS scheduling.
We conduct a simulation platform to verify the valid-
ity of our approach. Simulation results also show that
switches with different scheduling algorithms can im-
prove the delay performance in a multi-hop network.
The rest of the paper is organized as follows.
Section 2 elaborates the AFDX system model, in-
cluding traffic model, End System (ES) model and
Switch model. Section 3 studies rate-latency service
curve provided by multiplexer (MUX) with multiple
scheduling algorithms. Section 4 is the calculation
and analysis of the end-to-end delay, and gives an op-
timization in FCFS scheduling calculation. In Section
5, we use a simulation platform to verify our results.
The conclusion is drawn in section 6.
2 AFDX SYSTEM MODEL
AFDX network is made up of End Systems and
Switches. ES receives a variety of data from avionic
equipments and sends to a series of AFDX switches,
which quickly forward data to the appropriate desti-
nation ESs. For the purpose of using arrival curve α
and service curve β of Network Calculus (Le Boudec
and Thiran, 2001; Chang, 2000) to obtain the end-to-
end delay, the remaining section will build the model
for divers components in AFDX networks.
2.1 Traffic Model
In AFDX network, virtual link (VL) mechanism (GE,
2007; techSAT, 2008) is utilized to establish logical
communication links, which define logical unidirec-
tional connections from a source ES to multiple de-
terministic terminal ESs.
Each virtual link has a maximum bandwidth deter-
mined by two parameters: Bandwidth Allocation Gap
(BAG) and the maximum frame length (L
max
). BAG is
the minimum transmission time interval of adjacent
data frames on the virtual link, whose value ranges in
powers of 2 from 1 to 128ms. L
max
is the maximum
length of data frame allowed to be transmitted on the
virtual link, whose range is 64 ∼ 1518 bytes.
Bandwidth of a virtual link is then given by
(L
max
× 8× 1000) ÷ BAG bps.
2.2 End System Model
The primary function of ES is to provide safe and re-
liable avionics data exchange services, whose model
is shown in Figure 1.
AFDX
Comm Por
t
MUX
Physical
link
End Syste
m
AFDX
Comm Por
t
AFDX
Comm Por
t
AFDX
Comm Por
t
AFDX
Comm Por
t
AFDX
Comm Por
t
(ρ
1
, σ
1
)
(ρ
2
, σ
2
)
(ρ
n
, σ
n
)
VL 1
VL 2
VL n
regulator
regulator
regulator
Figure 1: End System Model.
Data coming from avionics devices are received
by communication ports and then are carried by vir-
tual link queues.
Based on BAG and L
max
of a virtual link, a (σ, ρ)-
traffic regulator (Cruz, 1991a; Loeser and Haertig,
2004) is used to pace adjacent frames of the virtual
link queue, making them be transmitted at intervals
that are not less than BAG (GE, 2007). The output
flow is then constrained by the arrival curve that is
express as an affine function α(t) = ρ × t + σ, where
ρ is the sustainable rate of flow, and σ is the outburst.
Multiplexer (MUX) (Cruz, 1991a; Cruz, 1991b) is
responsible for multiplexing the regulator outputs into
a physical link. MUX could employ a variety of poli-
cies to schedule virtual links, such as FCFS, SP, etc.
Note that the service curve of a virtual link depends
on the scheduling policy. Service curve depicts the
forwarding capability of network node, and is repre-
sented by the rate-latency function β(t) = R×(t − T),
where R is the service rate and T is the latency expe-
rienced in a network node. It provides a simple and
effective method to study various services offered by
network nodes in the worst cases.
2.3 Switch Model
An AFDX Switch receives and forwards virtual link
data, whose model is shown in Figure 2 (Charara
et al., 2006). Each port of switch is connected to at
most one ES. It is mainly constituted by packetizer,
forwarding processor and MUX.
ANALYSIS OF DETERMINISTIC END-TO-END DELAY IN MULTI-HOP AFDX AVIONICS NETWORK SYSTEM
435

Packetizer
Packetizer
Packetizer
MUX
MUX
MUX
Output
Port
Input
Por
t
Switch
Forwarding
Processor
Figure 2: Switch Model.
Switch receives data bits from input ports and puts
them into packetizers. When a data frame is com-
pletely received by a packetizer, it will be immedi-
ately moved to the MUX of appropriate output port
by forwarding processor based on static forwarding
table. This operation costs a technological forward-
ing latency that is considered to be fixed here. MUX
could also use a number of scheduling policies to out-
put arrival data just like those used in ES.
3 RATE-LATENCY SERVICE
CURVE IN MUX
In ES and switch, virtual link data ultimately enter
MUX and then are scheduled to output. This section
will give different service curves offered by MUX
corresponding to different scheduling algorithms.
A MUX can be seen as a combination of FCFS
queues and a scheduler. After entering the MUX, data
firstly go to FCFS queues to be buffered, and then the
scheduler selects and outputs buffered data in queues
according to the scheduling algorithm. On a typical
industrial configuration, physical links of AFDX net-
work are lightly loaded. Most of the links are loaded
at less than 15% and no link is loaded at more than
21% (Ridouard et al., 2008). The sustainable rate ρ
of the arrival VL is no more than the reserved rate al-
located to the virtual link, i.e. data backlog in queues
will not be unlimited growth to cause data overflow.
3.1 FCFS MUX
For a FCFS MUX with output rate C, only one FCFS
queue is used. Serving one virtual link, MUX outputs
data with service curve β(t) = C × t, i.e. as long as a
data frame is completely received by FCFS queue, it
is immediately scheduled to output by scheduler.
When VL1, VL2 with arrival curves α
1
, α
2
are
multiplexed in FCFS MUX, each virtual link meets
(σ
i
, ρ
i
)-restriction (i = 1, 2). From a property of FCFS
(Corollary6.2.3 in (Le Boudec and Thiran, 2001)),
service curve β
1
provided to α
1
by FCFS MUX can
be derived and given by β
1
(t) = (C − ρ
2
) × (t −
σ
2
C
).
In a general case where multiple virtual links with
arrival curves α
1
, α
2
, ..., α
i
, ..., α
n
are multiplexed in
FCFS MUX, each arrival virtual link meets (σ
i
, ρ
i
)-
restriction (i = 1, 2 ,..., n). To study the service curve
β
s
provided to a given VL S by MUX, we can di-
vide input virtual links into two parts. The first one
is a signal virtual link described by α
s
; The other one
is the aggregate flow of the rest input virtual links,
and can be expressed as α
′
(t) = ρ
′
× t + σ
′
, where
ρ
′
=
∑
i
ρ
i
− ρ
s
and σ
′
=
∑
i
σ
i
− σ
s
. According to the
second case, we have the following theorem.
Theorem 3.1 When n virtual links satisfying
α
1
∼ (σ
1
, ρ
1
), ..., α
s
∼ (σ
s
, ρ
s
), ..., α
n
∼ (σ
n
, ρ
n
) pass
through FCFS MUX with output rate C, the service
curve β
s
provided to VL S by FCFS MUX is given by
β
s,MUX
(t) = (C − ρ
′
) × (t −
σ
′
C
) (1)
The output curve satisfies α
∗
s
∼ (σ
∗
s
, ρ
s
), and outburst
is σ
∗
s
= ρ
s
×
σ
′
C
+ σ
s
, where ρ
′
=
∑
i
ρ
i
− ρ
s
, and σ
′
=
∑
i
σ
i
− σ
s
.
3.2 Static Priority MUX
For a static priority (SP) MUX, each FCFS queue re-
ceives particular virtual links corresponding to a pri-
ority level. For example, queue i receives i-priority
VLs. A bigger priority number i means a higher
priority level. The scheduler always chooses data
in the highest priority queue to output with a non-
preemptive manner.
Assuming that all arrival virtual links can be di-
vided into n subsets, each one corresponds to a prior-
ity level i (i=1, 2, ..., n) and is received by an appro-
priate priority queue among {Q
1
, Q
2
, ..., Q
n
}. Arrival
curve of every VL is represented by α
ij
, where i is
the priority level and j is an index. For the queue Q
k
with k-priority, arrival curve of input VLs is α
k
(t) =
ρ
k
× t + σ
k
, where ρ
k
=
∑
i=k
ρ
ij
and σ
k
=
∑
i=k
σ
ij
.
From the property of the SP scheduling (Proposi-
tion1.3.4 in (Le Boudec and Thiran, 2001)), we know
that if a server with output rate C serves two flows H
and L, then the high priority flow α
H
is guaranteed
by service curve with rate C and latency
L
L
max
C
, where
L
L
max
is the maximum frame size for the low priority
flow. The low priority flow α
L
is guaranteed by ser-
vice curve with rateC−ρ
H
and latency
σ
H
C−ρ
H
. We can
extend this result to the case of multiple flows and get
the following theorem.
Theorems 3.2 When n data flows satisfying
α
1
∼ (σ
1
, ρ
1
), ..., α
k
∼ (σ
k
, ρ
k
), ..., α
n
∼ (σ
n
, ρ
n
) pass
through SP MUX with output rate C, and the priority
of α
i
is i (i is bigger while its priority level is higher,
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
436

and 1 ≤ i ≤ n), the k-priority flow is guaranteed by a
rate-latency service curve
β
k
(t) = C
k
× (t − T
k
) (2)
where C
k
= C −
∑
i>k
ρ
i
, and T
k
=
∑
i>k
σ
i
+max
i<k
L
i
C
k
.
The formula (2) can be considered that the sched-
uler assigns output rate C
k
to the k-priority queue Q
k
,
and data of Q
k
will wait latency T
k
to be scheduled.
We could call T
k
the scheduling preparation time.
If k-priority queue Q
k
only receives data of one
VL, the result of (2) will be the service curve of this
VL. If Q
k
receives multiple VLs and VL S conforms
to (σ
ks
, ρ
ks
)-constraint, we would focus on the service
curve provided to a VL S among multiple virtual links
that enter queue Q
k
. According to previous analysis
of the FCFS scheduling, there has
β
s,MUX
(t)
= (C
k
− ρ
k
′
) × (t − T
k
−
σ
k
′
C
k
)
= (C −
∑
i≥k
ρ
ij
+ ρ
ks
) × (t −
∑
i≥k
σ
ij
−σ
ks
+max
i<k
L
ij
C−
∑
i>k
ρ
ij
)
The output curve satisfies α
∗
ks
∼ (σ
∗
ks
, ρ
ks
), and σ
∗
ks
=
ρ
ks
× (T
k
+
σ
k
′
C
k
) + σ
ks
, where ρ
k
′
=
∑
i=k
ρ
ij
− ρ
ks
and
σ
k
′
=
∑
i=k
σ
ij
− σ
ks
.
4 THE END-TO-END DELAY
CALCULATION
We defines the end-to-end delay as the maximum in-
terval that VL data experienced from the time emitted
from the traffic regulator in the source ES to that re-
ceived by the destination ES. As the propagation la-
tency on physical links is usually small compared to
that on ES and switch, it’s ignored in the following.
To compute the end-to-end delay using the “pay
burst only once” phenomenon, we first need to know
service curves provided by the source ES and every
switch that VL S passes and then convolute all service
curves to get the entire one provided by AFDX net-
work. The end-to-end delay can be computed based
on the maximum horizontal distance between the ar-
rival curve and the service curve, and expressed by
h(α, β) = sup[inf{T : T ≥ 0;α(s) ≤ β(s+ T)}].
“Pay burst only once” is an important phe-
nomenon in Network Calculus. It states that when
a data flow passes through two network nodes in se-
quence, the sum of the maximum delay on each node
is greater than the end-to-end delay. For example, if a
flow with arrival curve α passes through two network
nodes S
1
, S
2
with service curves β
1
, β
2
, and β
1
⊗ β
2
is the overall service curve supplied by S
1
, S
2
, we get
h(α, β
1
) + h(α
∗
, β
2
) ≥ h(α, β
1
⊗ β
2
),
where α
∗
is the arrival curve of the flow output from
S
1
. This phenomenon shows that the delay caused by
the burst of the input flow is calculated twice in the
former approach (Cen et al., 2008). For the case that
a flow through multiple nodes, this phenomenon also
exists, which is used to improve the end-to-end delay.
4.1 The End-to-End Service Curve
From the ES model presented in Section 2, it can be
seen that the virtual link delay on the ES is mainly
generated in MUX.
In a switch, the main components are packetizer,
forward processor, and MUX. The maximum delay
on packetizer is
L
max
C
and the service curve provided
to VL S can be expressed as δ(t −
L
max
C
), where C is
the maximum transmission rate of physical links con-
nected to each switch. Forward processor with a fixed
forwarding latency T
f
can be seen as a fixed delay
line (Cruz, 1991a) whose service curve is δ(t − T
f
).
The entire service curve offered by a switch can be
expressed as
β
s
= δ(t −
L
max
C
) ⊗ δ(t − T
f
) ⊗ β
s,MUX
= C
s
× (t −
L
max
C
− T
f
− T
ms
)
We assume that VL S passes n switches, and make
a convolution over all the service curves provided by
the source ES and switches. Finally the end-to-end
service curve β
e−e
offered to VL S is given by
β
e−e
= C
e
× (t −T
e
) = β
s0
⊗ β
s1
⊗ β
s2
⊗ ... ⊗β
sn
(3)
where β
si
is the service curve provided by the source
ES (i = 0) or switch i (i > 0).
When VL S shares its queue k with other virtual
links in node i, we not only take the scheduling delay
into account, but also add the latency caused by FCFS
service in FCFS queue. Thus, T
msi
= T
ki
+
σ
si
′
C
si
, and
β
si
=
(
(C
si
− ρ
si
′
) × (t −T
ki
−
σ
si
′
C
si
), i = 0
(C
si
− ρ
si
′
) × (t −T
f
−
L
max
C
− T
ki
−
σ
si
′
C
si
), i > 0
We put β
si
into (3) and obtain the service curve of
the entire AFDX network offered to VL S:
β
e−e
= min
0≤i≤n
(C
si
− ρ
si
′
) × [t − n× T
f
−n×
L
max
C
−
∑
0≤i≤n
(T
ki
+
σ
si
′
C
si
)]
(4)
4.2 The End-to-End Delay Calculation
By calculating the maximum horizontal distance be-
tween β
e−e
and arrival curve α
s
of VL S, the end-to-
end delay we acquire is
Delay
e−e
=
σ
s
C
e
+ T
e
=
σ
s
min
0≤i≤n
(C
si
−ρ
si
′
)
+ n× T
f
+ n×
L
max
C
+
∑
0≤i≤n
(T
ki
+
σ
si
′
C
si
)
(5)
ANALYSIS OF DETERMINISTIC END-TO-END DELAY IN MULTI-HOP AFDX AVIONICS NETWORK SYSTEM
437

To sum up, the calculation of the end-to-end de-
lay of virtual link requires specific parameters about
the network conflagration, such as forwarding ta-
ble of switch, scheduling policy, transmission band-
width, property of virtual link, L
max
, BAG and so on.
These would allow network nodes to supply different
scheduling services, making the design of the end-to-
end delay very flexible.
4.3 The Optimization in FCFS
Scheduling Calculation
In the research on the end-to-end delay in AFDX net-
works, we found that in many cases, frames of some
virtual links are transmitted on the same physical link
and output from the same port of nextconnected node.
Since frames are transmitted in serial on a physical
link and received in the order of arrival at connected
ES/Switch, this phenomenon has not been taken into
account in the FCFS scheduling calculation of (5),
and leads to a counteractivedelay estimation. In order
to optimize the delay calculation and to obtain bet-
ter results, the effect from sharing one physical link
by multiple VLs should be eliminated in the FCFS
scheduling calculation.
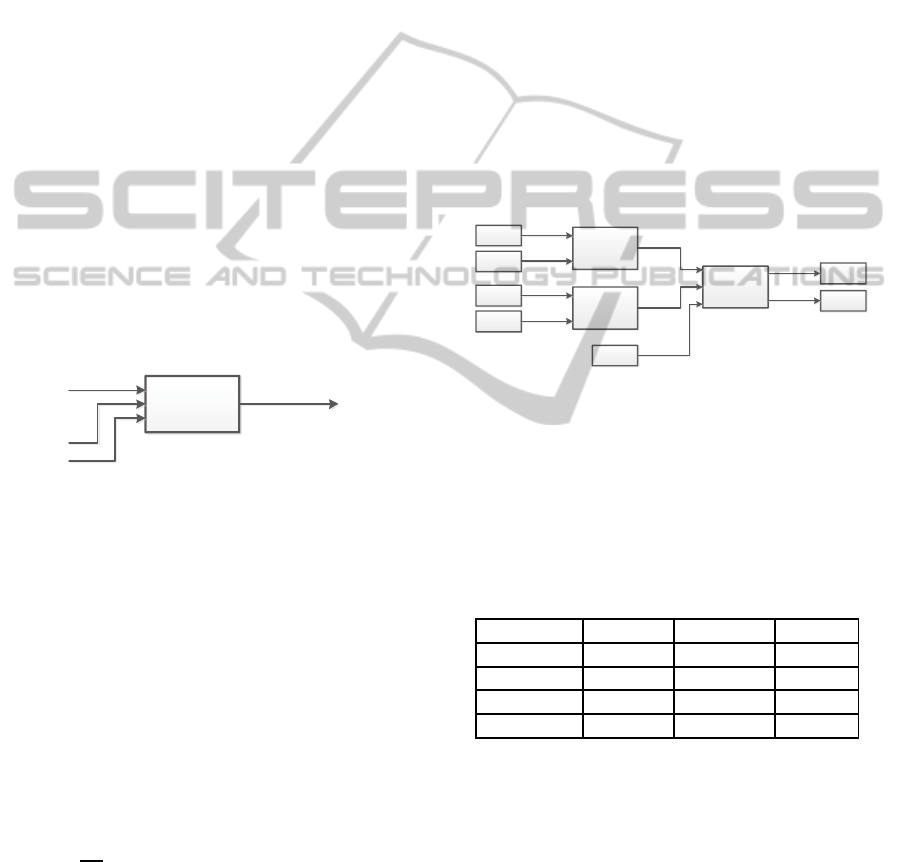
Node
(FCFS)
VLs 1~n
VL x
VLs 1~n,x,y
VL y
Figure 3: Example of the optimization.
We assume that VLs1 ∼ n share a physical link
in Figure 3, and meet (σ
i
, ρ
i
)-constraint (1 ≤ i ≤ n).
They are transmitted to a Node with FCFS schedul-
ing, and then output from a port with VL x and y.
Because of sharing a common link, the aggregate
flow z of VLs1 ∼ n is not characterized by α
z
(t) =
∑
1≤i≤n
ρ
i
× t +
∑
1≤i≤n
σ
i
, but by α
z
(t) =
∑
1≤i≤n
ρ
i
×
t + L
max
, where L
max
is the largest frame size of
VLs1 ∼ n (Bauer et al., 2009). The delay of flow z is
just influenced by flow x and y, and so are VLs1 ∼ n.
Service curves of VLs1 ∼ n are also the same with
flow z. So when obtaining the service curve of one of
VLs1 ∼ n, we just need to calculate the bursts of VL
x and y and ignore burst influences of VLs1 ∼ n, thus
decreasing
σ
si
′
C
si
in (5). For VL x and y, they are not
influenced by bursts of VLs1 ∼ n, but only by L
max
.
Obviously, taking into account actual virtual link path
distribution, would further optimize the computation
of the end-to-end delay.
5 EVALUATION AND ANALYSIS
In order to verify the validity of the end-to-end de-
lay calculation, simulation experiments are carried
out to measure the end-to-end delay of different vir-
tual links. The simulation results regarding different
scheduling strategies are compared with the calcu-
lated delay using the network calculus in this section.
5.1 Simulation Scenario
The experiments are carried on a small AFDX net-
work depicted in Figure 4. It is composed of 3 inter-
connected switches and 7 ESs. In these simulation ex-
periments, 7 VLs are studied with different schedul-
ing strategies, and the end-to-end delay of each vir-
tual link is obtained. Taking VL1 for example, its
source ES is ES1, destination ES is ES6, and the path
is ES1− S1− S3− ES6.
S1
ES 1
ES 2
S3
VL 1
VL 2
VL
3
S2
ES 3
ES 4
VL 4
VL 5
VL
6
ES 5
VL 7
VL1, VL2
VL 3
VL4, VL5
VL
6
ES 6
ES 7
VL 2, VL 3
VL 5, VL 6
VL 1, VL 4
VL 7
Figure 4: Small AFDX architecture and VL paths.
The latency of forwarding processor is assumed to
be a fix value 16µs in switches (Charara et al., 2006).
According to restrictions on BAG and L
max
in AFDX
network, the specific configuration of VL1 ∼ VL7 is
shown in Table 1. Each VL has a priority number: the
bigger the number, the higher the priority.
Table 1: Parameters of VLs.
VL NO. BAG L
max
priority
VL1, VL4 4000µs 120 bytes 3
VL2, VL5 16000µs 320 bytes 2
VL3, VL6 32000µs 600 bytes 1
VL7 2000µs 80 bytes 4
5.2 Simulation with TrueTime
Simulator
The networked control system simulation software -
TrueTime - is used as the experiment platform. It
is a Matlab/Simulink-based simulator for real-time
control systems (http://www.control.lth.se/truetime/).
TrueTime Toolbox includes two main interface mod-
ules - TrueTime Kernel and TrueTime Network. The
Kernel module is composed of flexible real-time ker-
nel, A/D and D/A converters, network interface and
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
438

Network Schedule 3
Network Schedule 2
Network Schedule 1
ES7
(TrueTime Kernel )
A/D
Interrupts
Rcv
D/A
Snd
Schedule
Monitors
P
ES6
(TrueTime Kernel )
A/D
Interrupts
Rcv
D/A
Snd
Schedule
Monitors
P
ES5
(TrueTime Kernel )
A/D
Interrupts
Rcv
D/A
Snd
Schedule
Monitors
P
ES4
(TrueTime Kernel )
A/D
Interrupts
Rcv
D/A
Snd
Schedule
Monitors
P
ES3
(TrueTime Kernel )
A/D
Interrupts
Rcv
D/A
Snd
Schedule
Monitors
P
ES2
(TrueTime Kernel )
A/D
Interrupts
Rcv
D/A
Snd
Schedule
Monitors
P
ES1
(TrueTime Kernel )
A/D
Interrupts
Rcv
D/A
Snd
Schedule
Monitors
P
m
m
m
AFDX Switch 3
(TrueTime Network )
Snd
Rcv
Schedule
3
AFDX Switch 2
(TrueTime Network )
Snd
Rcv
Schedule
2
AFDX Switch 1
(TrueTime Network )
Snd
Rcv
Schedule
1
2
1
Figure 5: TrueTime simulation platform.
external access. The network module provides vari-
ous network blocks, including CSMA/CD(Ethernet),
CSMA/AMP(CAN), Switched Ethernet, etc.
this simulation platform is built as an AFDX net-
work with transmission rate 100Mbps. Switched Eth-
ernet block is used as the basis for AFDX network
(switch function has been implemented in Switched
Ethernet block), and TrueTime Kernel is used as the
ES. Every VL is achieved with a periodic task. FCFS
is the default scheduling method in the switch. By
modifying the source code, we add SP and other
scheduling methods to the switch. Figure 5 illustrates
the implementation of simulation platform in True-
Time. Each VL meets its requirements of BAG and
the lengths of VL frames comply with the evenly dis-
tribution between 64 bytes to L
max
.
5.3 Computed End-to-End Delay
Bounds
The end-to-end delay of a virtual link can be com-
puted by a direct sum of the delay of all the nodes that
the virtual link traverses or by the application of “bay
burst only once”. Figure 6 shows the end-to-end de-
lay bounds for VL2 with different scheduling combi-
nations in S1 and S3 using these two methods respec-
tively. In the first method, because of the repetitive
burst calculations in a multi-hop network, it makes the
calculated delay larger. But in the second method, the
concatenation theorem is used to eliminate the effect
from the repetitive calculations, leading to a better re-
sult than that of the first method.
5.4 End-to-End Delay Analysis on
Different Scheduling Combinations
In simulation studies, FCFS scheduling policy is
adopted in ESs and various scheduling strategies in
Method1 Method2
0
50
100
150
200
250
300
350
400
delay ( s)
(FCFS, FCFS)
Method1 Method2
0
50
100
150
200
250
300
350
400
delay ( s)
(SP, SP)
Method1(Sum of node delays)
Method2(Pay burst ony once)
Figure 6: Analysis of the end-to-end delay with two calcu-
lation methods.
switches. Since the priorities of the virtual links are
not the same, we observed that when different combi-
nations of FCFS and SP are used in Switch1, Switch2
and Switch3, virtual links’ delay through the network
are different. Scheduling combination is represented
as (S1, S2, S3)-configuration. After several simula-
tions, the maximum delay values of virtual links are
obtained. The measured values and theoretical values
without optimization are shown in Figure 7.
In (FCFS, FCFS, FCFS)-configuration, theoreti-
cal values of virtual links with different priority are
not well distinguished. While SP scheduling being
added in the switch, the end-to-end delay correspond-
ing to each virtual link varies. In the (FCFS, FCFS,
SP) and (SP, SP, FCFS) configurations, each one only
uses SP scheduling once on virtual links, but the de-
lays of the same virtual links are different. In the (SP,
SP, SP) network, SP scheduling are applied twice in
the network, leading to a better distinguishment of
virtual links with three priority levels. Since network
1 2 3 4 5 6 7
0
200
400
VL No.
delay ( s)
(FCFS, FCFS, FCFS)
1 2 3 4 5 6 7
0
200
400
VL No.
delay ( s)
(FCFS, FCFS, SP)
1 2 3 4 5 6 7
0
200
400
VL No.
delay ( s)
(SP, SP, FCFS)
1 2 3 4 5 6 7
0
200
400
VL No.
delay ( s)
(SP, FCFS, FCFS)
1 2 3 4 5 6 7
0
200
400
VL No.
delay ( s)
(FCFS, SP, SP)
1 2 3 4 5 6 7
0
200
400
VL No.
delay ( s)
(SP, SP, SP)
Acutal measured maximum value
Theoretical maximum value without FCFS optimization
Theoretical maximum value with FCFS optimization
Figure 7: Each VL’s delay with different scheduling combi-
nations.
ANALYSIS OF DETERMINISTIC END-TO-END DELAY IN MULTI-HOP AFDX AVIONICS NETWORK SYSTEM
439

structure of Switch1 and Switch2 is symmetrical, sit-
uations of (FCFS, SP, FCFS) and (SP, FCFS, SP) are
similar to that of (SP, FCFS, FCFS) and (FCFS, SP,
SP). Thus they are ignored in Figure 7.
The difference between actual measured values
and theoretical ones is mainly due to the fact that the-
oretical values are results of the worst case delay anal-
ysis which is obviously pessimistic. In network cal-
culus, the worst case scenario is considered on each
node visited by each VL and the maximal possible
latency of competition is taken into account. This ap-
proach always gives guaranteed upper bounds on the
end-to-end delay that usually can never happen and
leads to impossible scenarios. For example, virtual
link data are not always to be sent with the maximal
frame length. Although theoretical values are cer-
tainly larger than actual measured values, they could
well reflect the overall trend of the delay variation.
When takinginto account FCFS optimization, the-
oretical delay bounds with optimization are better
than that without optimization and closer to actual
values (shown in Figure 7). In (SP, SP, FCFS) and
(SP, FCFS, FCFS) configurations, the delay of VL1
has not been significantly improved, because VL1
shares an output port of S3 with VL4 and VL7, but
doesn’t share the physical link from S1 to S3. Ow-
ing to the fact that FCFS isn’t applied in (SP, SP, SP)-
configuration, no optimization is obtained in this case.
5 10 15 20 25
0
100
200
300
400
500
600
700
800
Number of influence virtual links
delay ( s)
Actual maximum value
Theoretical maximum value without optimization
Theoretical maximum value with optimization
Figure 8: VL3’s end-to-end delay with influence links.
In order to better show the effect of FCFS opti-
mization, more influence virtual links are introduced
in the physical link that VL3 passes through from S1
to S3, sharing an output port of S3 with VL3. The
variations of VL3’s end-to-end delay with the increas-
ing number of influence links are displayed in the Fig-
ure 8 in (FCFS, FCFS, FCFS)-configuration.
From Figure 8, we notice that simulation values
change a little(274µs ∼ 454µs) and theoretical values
without optimization vary greatly(407µs ∼ 793µs).
This is mainly due to the fact that virtual links share
the same physical link and data are transmitted in se-
rial. With optimization, theoretical delay varies in
359µs ∼ 553µs, which has been significantly reduced.
6 CONCLUSIONS
This paper presents a network calculus-based ap-
proach for the end-to-end delay analysis in multi-hop
AFDX networks. Using the service curve model to
describe the transmitting service, we obtain an ana-
lytical upper bound on the end-to-end delay of VL.
In order to derive the overall service curve offered by
the whole network, we model various AFDX network
nodes and study diverse scheduling disciplines. This
approach can analyze most VLs in an AFDX network
that consists of different nodes with common schedul-
ing disciplines. Additionally, a simulation platform is
conducted to verify the validity of our approach.
REFERENCES
ARINC (2005). Arinc 664: Aircraft data network. part 7,
avionics full duplex switched ethernet (afdx) network.
Annapolis, Maryland, USA.
Bauer, H., Scharbarg, J.-L., and Fraboul, C. (2009). Ap-
plying and optimizing trajectory approach for per-
formance evaluation of afdx avionics network. In
Proceedings of the 14th International Conference
on Emerging Technologies and Factory Automation,
Mallorca, Spain. IEEE.
Cen, F., Xing, T., and Wu, K.-T. (2008). Real-time perfor-
mance evaluation of line topology switched ethernet.
International Journal of Automation and Computing,
05(4):376–380.
Chang, C. (2000). Performance Guarantees in communica-
tion networks. Springer, London.
Charara, H., Scharbarg, J.-L., Ermant, J., and Fraboul, C.
(2006). Methods for bounding end-to-end delays on
an afdx network. In Proceedings of the 18th Euromi-
cro Conference on Real-Time Systems.
Cruz, R. (1991a). A calculus for network delay, part i: Net-
work elements in isolation. IEEE Transactions on in-
formation theory, 37(1):114–131.
Cruz, R. (1991b). A calculus for network delay, part ii:
Network analysis. IEEE Transactions on information
theory, 37(1):132–141.
GE (2007). Afdx/arinc 664 protocol tutorial. Technical re-
port.
Le Boudec, J.-Y. and Thiran, P. (2001). Network Calculus,
A Theory of Deterministic Queuing Systems for the In-
ternet. Springer, Berlin.
Loeser, J. and Haertig, H. (2004). Low latency hard real-
time communication over switched ethernet. In Pro-
ceedings of Euromicro Conference on Real-Time Sys-
tems.
Ridouard, F., Scharbarg, J.-L., and Fraboul, C. (2008).
Stochastic upper bounds for heterogeneous flows us-
ing a static priority queueing on an afdx network.
Dans Journes FAC’2008, SVF/FRIA, 2008.
techSAT (2008). Afdx/arinc 664 tutorial. Technical report.
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
440