THE SPIRAL FACETS

A Uniﬁed Framework for the Analysis and Description of 3D Facial Mesh Surfaces

Naoufel Werghi, Harish Bhaskar

Dept. of Computer Engineering, Khalifa University, Sharjah Campus, Sharjah, U.A.E.

Youssef Meguebli, Haykel Boukadida

School of Science and Techniques, University of Tunis, Tunis, Tunisia

Keywords:

3D Face descriptors, Spiral facets, Feature localization, Geodesic curves, 3D Face orientation.

Abstract:

In this paper, we describe a framework for encoding 3D facial triangular mesh surface. We derive shape

information from the triangular mesh surface by exploiting speciﬁc arrangements of facets in the model. We

describe the foundations of the framework and adapt the framework for several original applications including:

face landmark detection, frontal face extraction, face orientation and facial surface representation. We validate

the framework through experimentation with raw 3D face mesh surfaces and demonstrate that the model allows

simpler implementation, more compact representation and encompasses rich shape information that can be

usefully deployed both locally and globally across the face in comparison to other standard representations.

1 INTRODUCTION

Face recognition is a central problem in biomet-

ric authentication, with applications including visual

surveillance and security. However, 2D face recogni-

tion systems are complicated by sensitivity to illumi-

nation conditions and pose variation. A popular al-

ternative to such 2D image-based systems is the use

of 3D face images whose richness and completeness

is often exploited to contribute in solving the inher-

ent limitations of 2D systems. However, there is a

growing need to faithfully encode raw 3D facial mesh

surface into a simple, structured and compact facial

representation.

There exist competing approaches to model 3D fa-

cial mesh surfaces. 3D shape can be represented in-

dependent of the co-ordinate system using the object-

centric representations. Such representations have in-

vited much attention in recent years due to their in-

variance to geometric transformations and their po-

tential to produce an reliable metric for facial shape

comparison.

In this paper, we propose a topological framework

for encoding 3D facial mesh surface that is concise

(encompasses dimensionality reduction, as a means

of improving the efﬁciency, or allowing the data com-

pression) and computationally efﬁcient. We denote

this representation as the ”spiral facets” and show

how this representation can be neatly adapted to ad-

dress several applications including but not restricted

to: facial landmarks detection, frontal face extraction,

face shape description and face pose computation.

2 RELATED WORK

In the context of 3D face recognition, we can catego-

rize the face shape representations into three classes,

namely: Local features representation, global feature

representation and hybrid representations.

Local feature representation methods employ fea-

tures derived from local face surface (at a limited

neighborhood). These attributes typically include cur-

vature measures (Moreno et al.,2006), and point sig-

natures (Chua et al.,2000). The derivation of local

features is performed with differential geometry tech-

niques that are intrinsically vulnerable to scaling and

data deﬁciencies (e.g., non-uniform resolution, pres-

ence of noise).

In contrast to the local representation, in global

representation, the facial features are derived from

the whole 3D face data. Wu (Wu et al.,2003) used

vertical and horizontal proﬁles of faces and Xu (Xu

et al.,2008) derived invariant curve and surface mo-

ments from 3D face data. In these methods, match-

Werghi N., Bhaskar H., Meguebli Y. and Boukadida H..

THE SPIRAL FACETS - A Uniﬁed Framework for the Analysis and Description of 3D Facial Mesh Surfaces.

DOI: 10.5220/0003362300300039

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 30-39

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

ing is performed by evaluating the similarity between

these entities. Other methods (Irfanoglu et al.,2004;

Lu and Jain,2005) superimpose the whole query 3D

facial image with the stored instances in the database,

and then evaluate the degree of overlapping to decide

whether or not they match. These approaches are

limited by their high computational cost. In (Lee et

al.,2003; Xu et al.,2004b) authors, extend the eigen-

faces paradigm developed in 2D face recognition to

the 3D case. This paradigm operates on a range or

depth image in which the pixel intensity represents

the ’z’ coordinate. However, these methods have in-

herited some of the shortcomings of 2D face identiﬁ-

cation, particularly with regard to the face pose, self-

occlusion and scaling. Other representations have

been developed based on geodesic entities (Bronstein

et al.,2003; Berretti et al.,2006; Samir et al., 2009),

these approaches aimed also to address face shape de-

formation. So did (Kakadiaris, 2007) with their de-

formable face model.

Finally, hybrid representation combines local and

global facial features. These methods were moti-

vated by psychological ﬁndings asserting that humans

equally rely on both local and global visual informa-

tion. Pan (Pan et al.,2003) augmented the eigenface

paradigm with face proﬁle. Xu (Xu et al.,2004a) de-

veloped a face representation deﬁned by a measure

of the similarity between the 3D face image and a

3D face template, and local shape variation around

local facial. landmarks (e.g., eyes and nose). Al-

Osaimi (Mian et al.,2007) employed a 2D histogram

that encompasses rank-0 tensor ﬁelds extracted at lo-

cal points of the facial surface and from the whole

face depth map data.

3 CONTRIBUTIONS

& STRUCTURE

The framework described in this paper, extracts or-

dered structured patterns from 3D triangular mesh

surface for a simple representation of facial surfaces.

We acknowledge that there are a number of repre-

sentations of 3D facial surfaces in the literature and

therefore, we list a set of 4 main characteristics of our

proposed ”spiral facets” representation that will dis-

tinguish it from other close face shape representation

(Berretti et al., 2006; Samir et al., 2009). These char-

acteristics include: a) simplicity and compactness:

the spiral facet representation is a single data struc-

ture, b) generalization: the facet spiral is a general-

ized representation of other popular 3D facial surface

representations and it is possible that we can derive

for example, the approximate geodesic rings structure

from the spiral facet, c) processing efﬁciency: our

representation also does not require any form of mesh

pre-processing, whereas in most other method mesh

regularization is often required and ﬁnally, d) compu-

tational complexity: out method is computationally

more efﬁcient. As we will explained in the end of

Section 4, we infer a complexity of (O(n)) in com-

parison to O(nlog(n)) in (Berretti et al., 2006; Samir

et al., 2009) which also requires a mesh regularization

of complexity O(n).

The other main novelty of the proposed frame-

work is in the adaptability of the framework for sev-

eral original applications including: a) nose tip local-

ization, b) frontal face extraction, c) 3D face shape

modeling d) 3D face pose computation and e) nose

proﬁle identiﬁcation.

We begin by describing our framework of 3D fa-

cial surface representation in Section 4. We then elab-

orate different applications of the proposed frame-

work in section 5 and conduct systematic experiments

on varied datasets for nose tip localization 5.1, 3D

frontal face extraction 5.2, face shape description 5.3,

3D face pose computation 5.4 and nose proﬁle iden-

tiﬁcation 5.5. In Section 6 we present concluding re-

marks and directions of future work.

4 THE SPIRAL FACETS

FRAMEWORK

In our framework, we derive a 3D facial surface rep-

resentation by constructing novel structured and or-

dered patterns in a 3D face triangular mesh surface.

The triangular mesh surface representation though is

simple, lacks an intrinsic ordered structure that allows

the facets in the mesh to be browsed systematically.

Consequently, storing the facets in the facet array is

usually arbitrary and does not follow any particular

arrangement. Therefore processing and analyzing tri-

angular mesh surfaces are more complex compared

with other intrinsically ordered shape modalities such

as range images. According to our framework, we

construct patterns exploiting topological properties of

a triangular mesh surface. These patterns include con-

centric rings of facets that can also be arranged in a

spiral-wise fashion. Our framework has been inspired

from the observation of the arrangement of triangu-

lar facets lying on closed contour of edges (Figure

1.a). From this, we can categorize the facets into two

groups: 1) facets having an edge on that contour that

seem to point outside the area delimited by the con-

tour (e.g. fout

and f out

in Figure 1.a). And 2)

facets having a vertex on the contour that point inside

the contour’s area. The facets in the second group

THE SPIRAL FACETS - A Unified Framework for the Analysis and Description of 3D Facial Mesh Surfaces

have an effect of ﬁlling gaps between facets in the

ﬁrst group. We call these two groups of facets as Fout

and Fgap facets and together, they form a kind of ring

structure. Using this ring facets we can derive a new

group of Fout facets that are one-to-one adjacent with

the Fgap facets of the previous ring, that will in-turn

form the basis of the subsequent rings (Figure 1.b).

We iterate this process to obtain a group of concen-

tric rings. When the initial contour is composed of

the edges of a given triangular facet, the rings will be

centered at that particular facet (Figure 1.c). More-

over, by imposing the last facet in the current ring to

be connected to the ﬁrst facet in the subsequent ring,

we obtain a sequence of facets arranged on a spiral-

wise fashion, i.e. sequence of facets starting at the

root facet and following a spiral path on the facial sur-

face. We dubbed this arrangement ”the spiral facet”.

(Figure 1.d). We also note that from the root triangle

3 different spiral facets can be generated depending

on the chosen facet among the three facets adjacent to

the root facet.

The algorithm for constructing a facet spiral start-

ing at a given facet t is as follows:

Algorithm GetSpiralFacets.

Rings = [t] , FoutFacets ← facets adjacent to t

For i=1: Number of rings

GapFacets ← FillGap(FoutFacets)

Ring ← FoutFacets + GapFacets

Append Ring to Rings

NewFoutFacets ← GetFoutFacest

(GapFacets,FoutFacets)

FoutFacets ← NewFoutFacets

End For

The algorithm GetSpiralFacets has computational

complexity of O(n) where n is the number of facets

in the facet spiral.

One of the main interesting characteristics of the

spiral facets representation is that facets at a given

ring are approximately at the same geodesic distance

from the root facet. The geodesic distance can be ap-

proximated to RingNumber ×L, where RingNumber

is the ring’s number in the facet spiral, and L is the

average length of the triangle’s edge. Therefore, it is

possible to use the spiral facets as a low cost alterna-

tive for computing an approximation of iso-geodesic

contours on the facial surface, compared to the stan-

dard O(nlog(n)) Dijkstra algorithm (Cormen et al.,

2001) (employed in (Samir et al., 2009)) and the

O(nlog(n)) fast marching method (Sethian and Kim-

mel, 1998) (used in (Berretti et al., 2006)). We com-

pute the geodesic path using the spiral facets in two

distinctive stages (Figure 1.e) . In the ﬁrst step, the

spiral facets are expanded from a source facet until

inspired from the observation of the arrangement of

triangular facets lying on closed contour of edges

(Figure 1.a) . From this, we can categorize the facets

into two groups: 1) facets having an edge on that

contour that seem to point outside the area delimited

by the contour (e.g. fout

and f out

in Figure 1.a).

And 2) facets having a vertex on the contour that

point inside the contour’s area. The facets in the

second group have an effect of ﬁlling gaps between

facets in the ﬁrst group. We call these two groups

of facets as Fout and Fgap facets and together, they

form a kind of ring structure. Using this ring facets

we can derive a new group of Fout facets that are

one-to-one adjacent with the Fgap facets of the

previous ring, that will in-turn form the basis of the

subsequent rings (Figure 1.b). We iterate this process

to obtain a group of concentric rings. When the initial

contour is composed of the edges of a given triangular

facet, the rings will be centered at that particular facet

(Figure 1.c). Moreover, by imposing the last facet in

the current ring to be connected to the ﬁrst facet in

the subsequent ring, we obtain a sequence of facets

arranged on a spiral-wise fashion, i.e. sequence

of facets starting at the root facet and following a

spiral path on the facial surface. We dubbed this

arrangement ”the spiral facet”. (Figure 1.d). We

also note that from the root triangle 3 different spiral

facets can be generated depending on the chosen

facet among the three facets adjacent to the root facet.

The algorithm for constructing a facet spiral

starting at a given facet t is as follows:

Algorithm GetSpiralFacets

Rings = [t] , FoutFacets ← facets adjacent to t

For i=1: Number of rings

GapFacets ← FillGap(FoutFacets)

Ring ← FoutFacets + GapFacets

Append Ring to Rings

NewFoutFacets ← GetFout-

Facest(GapFacets,FoutFacets)

FoutFacets ← NewFoutFacets

End For

The algorithm GetSpiralFacets has computa-

tional complexity of O(n) where n is the number of

facets in the facet spiral.

One of the main interesting characteristics of

the spiral facets representation is that facets at a

given ring are approximately at the same geodesic

distance from the root facet. The geodesic distance

can be approximated to RingNumber × L, where

RingNumber is the ring’s number in the facet spiral,

and L is the average length of the triangle’s edge.

fout

vout

fout

(a) (b)

(e)

(f)

Figure 1: a:Fout facets (dark) on the contour E

,..v

). The Fgap facets (clear) bridge the gap be-

tween pairs of consecutive Fout facets. b :Extraction of the

new Fout facets. Notice that the new Fout facets are one-

to-one adjacent to the Fgap facets. c: An examples of facet

spiral and its concentring rings. d: The same facet spiral

where the facets are arranged spiral-wise. e: Example of

a geodesic path computation: The facet spiral is expanded

from a source facet on the nose tip until the the destina-

tion facet is reached, then the geodesic path is extracted by

tracing back the source facet. f: examples of geodesic paths

between the nose tip and facets on a periphery ring of a facet

spiral.

Therefore, it is possible to use the spiral facets as a

low cost alternative for computing an approximation

of iso-geodesic contours on the facial surface, com-

pared to the standard O(nlog(n)) Dijkstra algorithm

(Cormen et al., 2001) (employed in (Samir et al.,

2009)) and the O(nlog(n)) fast marching method

(Sethian and Kimmel., 1998) (used in (Berretti et al.,

2006)). We compute the geodesic path using the

spiral facets in two distinctive stages (Figure 1.e) . In

the ﬁrst step, the spiral facets are expanded from a

source facet until the destination facet is reached (i.e.,

found in the last ring). In the second step, the rings

(f)

Figure 1: a): Fout facets (dark) on the contour E

,..v

). The Fgap facets (clear) bridge the gap be-

tween pairs of consecutive Fout facets. b :Extraction of the

new Fout facets. Notice that the new Fout facets are one-

to-one adjacent to the Fgap facets. c: An examples of facet

spiral and its concentring rings. d: The same facet spiral

where the facets are arranged spiral-wise. e: Example of

a geodesic path computation: The facet spiral is expanded

from a source facet on the nose tip until the the destina-

tion facet is reached, then the geodesic path is extracted by

tracing back the source facet. f: examples of geodesic paths

between the nose tip and facets on a periphery ring of a facet

spiral.

the destination facet is reached (i.e., found in the last

ring). In the second step, the rings are browsed back-

wards, starting from the destination facet, and reiter-

ated looking for the nearest connected facet in the pre-

vious ring until the source facet is reached. Since the

algorithm GetSpiralFacet intrinsically computes the

connectivity between facets in adjacent rings, the sec-

ond stage has a complexity of O(RingNumber). (Fig-

ure 1.f) depicts facets on the geodesic paths between

the nose tip and facets located at a given ring of the

facet spiral.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

5 APPLICATIONS

In this section of the paper, we exhibit the generality

of the spiral facets framework by adapting it for sev-

eral 3D face applications. One of the critical steps to-

wards face recognition is the localization of features.

In the initial attempt to localize 3D facial features us-

ing the ”spiral facets” representation, we ﬁrst present

the nose tip detection application in Section 5.1. We

substantially elaborate on this part since the rest of

the applications depends on it. Next, we describe the

algorithm to extract the frontal face from the raw 3D

face scan by propagating rings starting from the de-

tected nose tip in Section 5.2. Face shape descrip-

tion and pose identiﬁcation are also important com-

ponents particularly to model based matching of 3D

faces. In Sections 5.3,5.4 we explore an approach

for face shape description and face pose computation

using the spiral facets framework. Finally, we also

exploit the geodesic properties of the spiral facets to

extract the nose proﬁle from 3D face scans in Sec-

tion 5.5.

5.1 Nose Tip Detection

Face landmarks detection is critical to face recogni-

tion and nose tip detection in particular has a capital

role due to its center position and saliency. A majority

of 3D face analysis techniques are anchored to detect-

ing the nose tip. The problem of nose tip detection has

been approached using heuristic rules-based methods

(Colbry et al., 2005; Heseltine et al., 2008). Such

methods requires a restricted face pose. This issue

was addressed to some extent by shape descriptors-

based methods (Segundo et al., 2007; Wang et al.,

2008) that are speciﬁcally invariance to geometric

transformation. However, the presence of noise has

often affected the reliability of such systems. Statisti-

cal methods (Ruiz and Illingworth,2008; Romero and

Pears, 2009) employed a landmarks model, obtained

via training. This model is registered to the face data

in order to get an approximate landmark locations,

which are further reﬁned in an iterative manner. This

method inherits the problems of model registration;

such as the need of prior pose information. Apart

of (Xu et al., 2006) most approaches that dealt with

face landmarks detection treated a pre-processed data,

in which the 3D face surface has been cropped and

smoothed. The method in (Xu et al., 2006) uses a hi-

erarchical ﬁltering scheme employing shape descrip-

tors and a local nose tip shape model. The method

is robust, but, revealed cases of false detection for

some instance where clothing deformation matches

the nose tip statistical model.

We propose an application of the 3D spiral facets

for nose tip detection from raw 3D triangular mesh fa-

cial surfaces. Our method is inspired from the obser-

vation that the regions around some facial landmarks

are characterized by low mesh quality. These result

from gaps (in the nostrils) and reﬂection effects (at

the eyes) (see Figure 2.a). To measure and assess the

quality of the mesh surface, we present an original

framework using which we extract a group of candi-

date triangular facets. In the second stage of our algo-

rithm, we ﬁnd the single facet that corresponds to the

nose tip from the group of candidate triangle facets

using a series of ﬁltering steps.

5.1.1 Assessing the Regularity of the Mesh

Tessellation

The term mesh quality is context driven and tightly

linked to the subsequent use of the constructed mesh

(Frey and Borouchaki, 1999), therefore there is no

standard framework for assessing the quality of tri-

angular mesh surface for raw 3D facial surface scan.

are browsed backwards, starting from the destination

facet, and reiterated looking for the nearest connected

facet in the previous ring until the source facet is

reached. Since the algorithm GetSpiralFacet intrin-

sically computes the connectivity between facets in

adjacent rings, the second stage has a complexity

of O(RingNumber). (Figure 1.f) depicts facets on

the geodesic paths between the nose tip and facets

located at a given ring of the facet spiral.

5 Applications

In this section of the paper, we exhibit the gen-

erality of the spiral facets framework by adapting it

for several 3D face applications. One of the critical

steps towards face recognition is the localization of

features. In the initial attempt to localize 3D facial

features using the ”spiral facets” representation, we

ﬁrst present the nose tip detection application in Sec-

tion 5.1. We substantially elaborate on this part since

the rest of the applications depends on it. Next, we

describe the algorithm to extract the frontal face from

the raw 3D face scan by propagating rings starting

from the detected nose tip in Section 5.2. Face shape

description and pose identiﬁcation are also important

components particularly to model based matching of

3D faces. In Sections 5.3,5.4 we explore an approach

for face shape description and face pose computation

using the spiral facets framework. Finally, we also

exploit the geodesic properties of the spiral facets to

extract the nose proﬁle from 3D face scans in Sec-

tion 5.5.

5.1 Nose Tip Detection

Face landmarks detection is critical to face recog-

nition and nose tip detection in particular has a

capital role due to its center position and saliency. A

majority of 3D face analysis techniques are anchored

to detecting the nose tip. The problem of nose tip

detection has been approached using heuristic rules-

based methods (Colbry et al., 2005; Heseltine et al.,

2008). Such methods requires a restricted face pose.

This issue was addressed to some extent by shape

descriptors-based methods(Segundo et al., 2007;

Wang et al., 2008) that are speciﬁcally invariance

to geometric transformation. However, the presence

of noise has often affected the reliability of such

systems. Statistical methods (Ruiz and Illingworth,

2008; Romero and Pears, 2009) employed a land-

marks model, obtained via training. This model

is registered to the face data in order to get an

approximate landmark locations, which are further

reﬁned in an iterative manner. This method inherits

the problems of model registration; such as the need

of prior pose information. Apart of (Xu et al., 2006)

most approaches that dealt with face landmarks

detection treated a pre-processed data, in which the

3D face surface has been cropped and smoothed.

The method in (Xu et al., 2006) uses a hierarchical

ﬁltering scheme employing shape descriptors and a

local nose tip shape model. The method is robust, but,

revealed cases of false detection for some instance

where clothing deformation matches the nose tip

statistical model.

We propose an application of the 3D spiral facets

for nose tip detection from raw 3D triangular mesh

facial surfaces. Our method is inspired from the

observation that the regions around some facial

landmarks are characterized by low mesh quality.

These result from gaps (in the nostrils) and reﬂection

effects (at the eyes) (see Figure 2.a). To measure and

assess the quality of the mesh surface, we present an

original framework using which we extract a group of

candidate triangular facets. In the second stage of our

algorithm, we ﬁnd the single facet that corresponds

to the nose tip from the group of candidate triangle

facets using a series of ﬁltering steps.

5.1.1 Assessing the regularity of the mesh

tessellation

The term mesh quality is context driven and tightly

linked to the subsequent use of the constructed mesh

(Frey and Borouchaki, 1999), therefore there is no

standard framework for assessing the quality of tri-

angular mesh surface for raw 3D facial surface scan.

Our proposed technique measures to what extent a tri-

(a) (b)

Figure 2: a: A sample triangular mesh facial surface. Notice

the mesh irregularities at the nostrils, and the the eyes areas.

b: Computation of the error ∆

at each facet. Dark areas

correspond to a large error.

angular mesh is close to an ideal mesh composed of

equal-sized equilateral triangles at a given neighbor-

hood. In such mesh, we can show easily that the num-

ber of triangles across the concentric rings that from

the facet spiral follow arithmetic progression:

(a) (b)

Figure 2: a): A sample triangular mesh facial surface. No-

tice the mesh irregularities at the nostrils, and the the eyes

areas. b): Computation of the error ∆

at each facet. Dark

areas correspond to a large error.

Our proposed technique measures to what extent

a triangular mesh is close to an ideal mesh composed

of equal-sized equilateral triangles at a given neigh-

borhood. In such mesh, we can show easily that the

number of triangles across the concentric rings that

from the facet spiral follow arithmetic progression:

nrt(n + 1) = nrt(n) + 12 (1)

where nrt(n) and nrt(n + 1) are the number of trian-

gles in the ring n and n + 1 respectively. Therefore,

the sequence

in an ideal mesh, starting at a root

facet, is [12,24,36, ,12n]. This condition will not be

satisﬁed at surface areas where the uniformity of the

mesh tessellation is corrupted. Based on this, we pro-

pose the following local criterion for evaluating the

mesh tessellation uniformity.

∆

kη

−

, (2)

THE SPIRAL FACETS - A Unified Framework for the Analysis and Description of 3D Facial Mesh Surfaces

where η

(respectively

) is the sequence represent-

ing the number of triangles across a group of n con-

centric rings in a arbitrary mesh (respectively an ideal

mesh). Figure 2.b depicts ∆

computed at each facet

of a sample 3D raw facial data.

5.1.2 Cascading ﬁlters

After computing the error ∆

(Figure 3.b), we retain

those facets having a ∆

above a certain threshold.

The group of facets extracted from this level of ﬁl-

tering (dubbed Group1), contains a majority of facets

in the neighborhood of the nostrils and eyes and also

other facets spread mostly across the ears, clothes and

the periphery areas in the raw mesh surface (as in Fig-

ure 3.c). In the second level of our cascaded ﬁlter-

ing implementation, we apply prior information de-

rived from the topological characteristics of the raw

face scan to extract the central facets corresponding

to a potential landmark. As Figure 3.a shows, the

face scan is composed of several fragmented mani-

fold pieces which includes the face, parts of the hair,

neck, and upper torso. We initialize a two-phase ﬁlter

where in the ﬁrst phase, facets from Group1 generat-

ing more than 18 rings are selected. By doing this,

we capture facets located within the vicinity of the

central face, and naturally discard those which are lo-

cated at the surface periphery or at small surface frag-

ments. We set the threshold to 18 as it is about half the

maximum number of rings in a typical facial surface.

In the subsequent phase, we select from the obtained

facets those scoring the 10 highest number of rings

(Figure 3.d). To these facets we add those locates at

their neighborhoods (by expanding 4 rings-facet spi-

ral around each one of them). We called the so ob-

tained group of facets, Group 2 facets.

In the third level, we employ a model-based

matching method based on the standard Geometric

Histogram (GH) local shape descriptor (Ashbrook et

al., 1998). The GH is a 2D accumulator that describes

a pairwise relationship between a central facet and

each of it surrounding facets within a given neighbor-

hood. This relationship in the form of the angles (α)

between the central facet normals and all the other

facets’ normals, and the range of perpendicular alge-

braic distances (ρ) from the plane in which the cen-

tral facet lies to all the other facets in the neighbor-

hood. These measurements are entered in the dis-

crete angle distance 2D accumulator, thus obtaining

a kind of distribution that characterizes the relation-

ship between the root facet and its neighbors. The

neighborhood is constructed by generating a six-rings

spiral facets around a central facet. At this level, the

GH of each candidate facet is matched with the sta-

tistical model of GH of the nose tip neighborhood.

nrt(n + 1) = nrt(n) + 12 (1)

where nrt(n) and nrt(n + 1) are the number of trian-

gles in the ring n and n + 1 respectively. Therefore,

the sequence

in an ideal mesh, starting at a root

facet, is [12,24,36, ,12n]. This condition will not be

satisﬁed at surface areas where the uniformity of the

mesh tessellation is corrupted. Based on this, we pro-

pose the following local criterion for evaluating the

mesh tessellation uniformity.

∆

∥η

−

∥

, (2)

where η

(respectively

) is the sequence represent-

ing the number of triangles across a group of n con-

centric rings in a arbitrary mesh (respectively an ideal

mesh). Figure 2.b depicts ∆

computed at each facet

of a sample 3D raw facial data.

5.1.2 Cascading ﬁlters

After computing the error ∆

(Figure 3.b), we retain

those facets having a ∆

above a certain threshold.

The group of facets extracted from this level of ﬁlter-

ing (dubbed Group1), contains a majority of facets

in the neighborhood of the nostrils and eyes and also

other facets spread mostly across the ears, clothes

and the periphery areas in the raw mesh surface (as

in Figure 3.c). In the second level of our cascaded

ﬁltering implementation, we apply prior information

derived from the topological characteristics of the raw

face scan to extract the central facets corresponding

to a potential landmark. As Figure 3.a shows, the face

scan is composed of several fragmented manifold

pieces which includes the face, parts of the hair,

neck, and upper torso. We initialize a two-phase

ﬁlter where in the ﬁrst phase, facets from Group1

generating more than 18 rings are selected. By doing

this, we capture facets located within the vicinity of

the central face, and naturally discard those which are

located at the surface periphery or at small surface

fragments. We set the threshold to 18 as it is about

half the maximum number of rings in a typical facial

surface. In the subsequent phase, we select from

the obtained facets those scoring the 10 highest

number of rings (Figure 3.d). To these facets we add

those locates at their neighborhoods (by expanding

4 rings-facet spiral around each one of them). We

called the so obtained group of facets, Group 2 facets.

In the third level, we employ a model-based

matching method based on the standard Geometric

Histogram (GH) local shape descriptor (Ashbrook

et al., 1998). The GH is a 2D accumulator that

(a) (b) (c)

(d) (e) (f)

(g)

Figure 3: Nose tip detection stages a: raw 3D face mesh

surface. b: computation of the mesh quality criterion ∆

. c:

Selection of the facets scoring a ∆

above a certain thresh-

old. d: Elimination of the facets at the periphery areas and

selection of the most central facets. e: Detection of candi-

date facets via Geometric Histogram matching. f: selection

of the nose tip facet. g: Detected nose tips on some face

samples.

describes a pairwise relationship between a central

facet and each of it surrounding facets within a

given neighborhood. This relationship in the form

of the angles (α) between the central facet normals

and all the other facets’ normals, and the range of

perpendicular algebraic distances (ρ) from the plane

in which the central facet lies to all the other facets in

the neighborhood. These measurements are entered

in the discrete angle distance 2D accumulator, thus

obtaining a kind of distribution that characterizes the

relationship between the root facet and its neighbors.

The neighborhood is constructed by generating a six-

rings spiral facets around a central facet. At this level,

the GH of each candidate facet is matched with the

statistical model of GH of the nose tip neighborhood.

This model is obtained from 100 face data samples,

whereby we averaged the 100 GHs derived from their

corresponding nose tip neighborhoods. The matching

criterion used to evaluate the closeness of two GHs h

and h

is the Bhattacharya distance:

i j

Bhattacharya

∑

α,ρ



(α,ρ)



(α,ρ). (3)

Since the nose tip can be located as an area rather

a single point, and the matching is performed using an

average model, we select the facets having a matching

(g)

Figure 3: Nose tip detection stages a: raw 3D face mesh

surface. b: computation of the mesh quality criterion ∆

. c:

Selection of the facets scoring a ∆

above a certain thresh-

old. d: Elimination of the facets at the periphery areas and

selection of the most central facets. e: Detection of candi-

date facets via Geometric Histogram matching. f: selection

of the nose tip facet. g: Detected nose tips on some face

samples.

This model is obtained from 100 face data samples,

whereby we averaged the 100 GHs derived from their

corresponding nose tip neighborhoods.

The matching criterion used to evaluate the close-

ness of two GHs h

and h

is the Bhattacharya dis-

tance:

i j

Bhattacharya

∑

α,ρ

(α,ρ)

(α,ρ). (3)

Since the nose tip can be located as an area rather

a single point, and the matching is performed using an

average model, we select the facets having a matching

score at a given distance from the maximum. This set

of facets, called Group 3, is deﬁned by:

N = {t \Max

−5σ ≤ D

Bhattacharyya

(GH

,GH) ≤ Max

}

(4)

where sigma is the variance of Bhattacharyya dis-

tances between the GHs samples used for computing

the mean GH model. Figure 3.e depicts and instance

of this set. In the ﬁnal level of our cascaded ﬁltering

implementation, we further reﬁne the location of the

nose tip by computing for each facet in Group 3, the

rank-2 tensor ﬁeld (Mian et al., 2007)

T =

∑

i=1

A|~r

(5)

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

where n is the number of facets in the facet’s neigh-

borhood. a

is the area of the ith facet, ~r

is a vector

from its center to central facet’s center and A is the

total neighbourhood’s area. T represents the covari-

ance of ~r and encodes the local neighborhood varia-

tion which is reﬂected in its three eigenvalues. So in

this level we select the facet having the largest eigen-

value as the one corresponding to the nose tip. Figure

3.(f,g) shows nose tips detected on some face sam-

ples.

5.2 Frontal Face Extraction

Using the same framework for assessing mesh qual-

ity,and exploiting the knowledge of the nose tip area,

we present an extension to extract the frontal face area

from the raw unprocessed 3D facial data. A popu-

lar technique to extract frontal faces discussed in the

literature is using a cropping sphere centered at the

nose tip (e.g. in (F. R. et al., 2008; Nair and Caval-

laro, 2009)). However such a technique is sensitive to

scale variance. An alternative approach discussed in

(R. Niese et al., 2007) uses 3D point clustering based

on texture information. This method requires the tex-

ture map to be available, and is unstable for head ori-

entations greater than ±45

◦

In our approach, we exploit the spiral facets to

develop an intrinsically scale-invariant method for

frontal face extraction. Its implementation is as fol-

lows: For each facet t within a 5-ring size nose tip

neighborhood, we generate a set of facets R (t) using

the GetFacetSpiral algorithm initialized at t and with

the stop condition set to ’Rings reaches a border of

the surface’. Following which, we merge all the sets

R (t) into a single set F using:

F = ]

t∈N

R (t) (6)

where ] is the exclusive union. This procedure en-

sures a maximum coverage of the central face area.

An illustration of the frontal face extraction pro-

cess is shown in Figure 4.

5.3 Face Shape Description

We discuss the 3rd application of the spiral facets

framework in the form of the face shape description.

From the spiral facets we derive a discrete 3D curve

represented by a sequence of points P

,...,P

where

each point is the center of a triangle facet. This curve

is invariant to translation and rotation. The curve ex-

hibits some irregularity inherited from the raw trian-

gular mesh. Rather than performing a costly mesh

regularization preprocessing stage, we simply apply

basic spatial smoothing to the points followed by a 3D

score at a given distance from the maximum. This set

of facets, called Group 3, is deﬁned by:

N = {t \Max

−5σ ≤D

Bhattacharyya

(GH

,GH) ≤Max

}

(4)

where sigma is the variance of Bhattacharyya dis-

tances between the GHs samples used for computing

the mean GH model. Figure 3.e depicts and instance

of this set. In the ﬁnal level of our cascaded ﬁltering

implementation, we further reﬁne the location of the

nose tip by computing for each facet in Group 3, the

rank-2 tensor ﬁeld ((Mian et al., 2007))

T =

∑

i=1

⃗r

A|⃗r

∥

(5)

where n is the number of facets in the facet’s neigh-

borhood. a

is the area of the ith facet, ⃗r

is a vector

from its center to central facet’s center and A is the

total neighbourhood’s area. T represents the covari-

ance of ⃗r and encodes the local neighborhood varia-

tion which is reﬂected in its three eigenvalues. So in

this level we select the facet having the largest eigen-

value as the one corresponding to the nose tip. Figure

3.(f,g) shows nose tips detected on some face sam-

ples.

5.2 Frontal Face Extraction

Using the same framework for assessing mesh

quality,and exploiting the knowledge of the nose tip

area, we present an extension to extract the frontal

face area from the raw unprocessed 3D facial data. A

popular technique to extract frontal faces discussed

in the literature is using a cropping sphere centered

at the nose tip (e.g. in (F.R. et al., 2008; Nair and

Cavallaro, 2009)). However such a technique is

sensitive to scale variance. An alternative approach

discussed in (R.Niese et al., 2007) uses 3D point

clustering based on texture information. This method

requires the texture map to be available, and is

unstable for head orientations greater than ±45

◦

In our approach, we exploit the spiral facets to

develop an intrinsically scale-invariant method for

frontal face extraction. Its implementation is as

follows: For each facet t within a 5-ring size nose

tip neighborhood, we generate a set of facets R (t)

using the GetFacetSpiral algorithm initialized at t

and with the stop condition set to ’Rings reaches a

border of the surface’. Following which, we merge

all the sets R (t) into a single set F using:

F = ⊎

t∈N

R (t) (6)

where ⊎ is the exclusive union. This procedure

ensures a maximum coverage of the central face area.

An illustration of the frontal face extraction process

is shown in Figure 4.

Figure 4: Extraction of the frontal face area: from the each

facet in the nose tip neighborhood we propagate rings until

a border is reached. Then we merge the obtained sets to get

the frontal face area.

5.3 Face Shape Description

We discuss the 3rd application of the spiral facets

framework in the form of the face shape description.

From the spiral facets we derive a discrete 3D curve

represented by a sequence of points P

,...,P

where

each point is the center of a triangle facet. This curve

is invariant to translation and rotation. The curve ex-

hibits some irregularity inherited from the raw trian-

gular mesh. Rather than performing a costly mesh

regularization preprocessing stage, we simply apply

basic spatial smoothing to the points followed by a 3D

Chord Length parametrization and cubic spline inter-

polation (Piegl and Tiller, 2006). The parametrization

is performed as follows:

= 0 t

(

∑

i=1

−P

i−1

= 1; (7)

Since the chord length parametrization in an ap-

proximation of the area-length parametrization, the

parameter space of the spiral curve generates a se-

quence of 3D points at nearly uniform intervals. Fig-

ure 5.a shows a portion of 3D spiral curve starting

Figure 4: Extraction of the frontal face area: from the each

facet in the nose tip neighborhood we propagate rings until

a border is reached. Then we merge the obtained sets to get

the frontal face area.

Chord Length parametrization and cubic spline inter-

polation (Piegl and Tiller, 2006). The parametrization

is performed as follows:

= 0 t

(

∑

i=1

−P

i−1

= 1; (7)

Since the chord length parametrization in an ap-

proximation of the area-length parametrization, the

parameter space of the spiral curve generates a se-

quence of 3D points at nearly uniform intervals. Fig-

ure 5.a shows a portion of 3D spiral curve starting

at the nose tip. Figure 5.b shows an instance of 3D

spiral curve spanning the whole face superimposed

on the original surface. This spiral 3D curve encap-

sulates the facial shape variation at a both local and

global scale. Moreover, since the 3D spiral curve is

attached to the facial surface, it can be augmented to

the normal to the face surface at each of points. We

presume that our facial representation spiral facets is

the only model that encode such facial shape varia-

tion into a single mono-dimensional structure. In the

same vein, we construct a 3D closed curve from each

ring in the spiral facets. We obtain a group of con-

centric curves C

,k = 1..N centered at the nose tip.

We can easily control the density of these curves by

a simple subsampling as illustrated in Figure 5.(c).

The C

curves inherit from the spiral facet rings the

iso-geodesic property. Therefore they can be used as

low-cost alternative of the iso-gedesic closed curves

employed in (Samir et al.,2009), which do also re-

quire a mesh regularization.

THE SPIRAL FACETS - A Unified Framework for the Analysis and Description of 3D Facial Mesh Surfaces

at the nose tip. Figure 5.b shows an instance of 3D

spiral curve spanning the whole face superimposed

on the original surface. This spiral 3D curve encap-

sulates the facial shape variation at a both local and

global scale. Moreover, since the 3D spiral curve is

attached to the facial surface, it can be augmented to

the normal to the face surface at each of points. We

presume that our facial representation spiral facets is

the only model that encode such facial shape varia-

tion into a single mono-dimensional structure. In the

same vein, we construct a 3D closed curve from each

ring in the spiral facets. We obtain a group of con-

centric curves C

,k = 1..N centered at the nose tip.

We can easily control the density of these curves by

a simple subsampling as illustrated in Figure 5.(c).

The

curves inherit from the spiral facet rings the

iso-geodesic property. Therefore they can be used as

low-cost alternative of the iso-gedesic closed curves

employed in (Samir et al., 2009), which do also re-

quire a mesh regularization.

(a) (b)

(c)

Figure 5: a.: A piece of 3D spiral curve emanating from the

nose tip. b: The full spiral curve superimposed on the facial

surface. Facial closed-curves at decreasing sampling rate.

5.4 Face Pose Computation

The computation of the face pose is a critical step to

model based localization and recognition tasks. In

this section, we brief on the details of how our frame-

work is adapted to approximate the face pose of a 3D

facial surface. By face pose, we refer to the coordi-

nate system (O,⃗u,⃗v,⃗w), attached to the face, in which

the origin is the nose tip, and the axis are the gaze di-

rection, the normal to the face symmetry plane, and

the view up direction. In order to determine the face

pose: we begin by grouping all the points that form

the discrete curves C

determined in the previous sec-

tion, and simply compute their principal axes via the

standard PCA analysis. Since the curves C

inherit the

symmetry property of the facet with respect to face’s

symmetry plane, it is expected that the PCA method

will produce axis that match the face pose to a reason-

ably good extent. In Figure 6.a we depict some exam-

ples of face pose axis plotted on the raw facial scans.

From the face pose, we also derive the face symmetry

plane, having as normal the vector⃗v and including the

nose tip. Some examples of the symmetry plane are

illustrated in Figure 6(2nd row). We assess the pose

estimation methods in two ways, 1) by aligning pairs

of different face scans of the same individuals using

their estimated poses and 2) by comparing the sym-

metry plane computed by our method with symmetry

plan derived from ground truth data. The ﬁrst experi-

ment was conducted with a group of faces comprising

instances of raw facial scan in neutral expression and

their sad expression counterpart. The facial surface

in this last group are cropped. Figure 6 (3rd and 4th

row) shows some aligned instances. It is clearly ob-

servable that alignments exhibit an acceptable accu-

racy, and thus can be used for a suitable initialization

for the iterative registration algorithms such as the it-

erative closest point method (ICP).

Figure 6: Computation of the face pose (1st row) and deduc-

tion of the face symmetry plane for some face samples (2nd

row). 3rd and 4rth rows:Alignment of cropped instances of

faces exhibiting sad facial expression to their counterparts

raw images in a neutral expressions.

In the second method of assessment, we consider

symmetry plane estimation error as the angle between

the the two normals of the estimated and the actual

planes. We computed the estimation error for a group

of 200 3D face instances (100 neutrals and 100 sads)

and have found a standard deviation error of 2 degree

for a mean error of 0.03 degree, and a maximum error

of 4 degree.

In addition, we also assess the stability of the

Figure 5: a): A piece of 3D spiral curve emanating from

the nose tip. b): The full spiral curve superimposed on the

facial surface. Facial closed-curves at decreasing sampling

rate.

5.4 Face Pose Computation

The computation of the face pose is a critical step to

model based localization and recognition tasks. In

this section, we brief on the details of how our frame-

work is adapted to approximate the face pose of a 3D

facial surface. By face pose, we refer to the coordi-

nate system (O,~u,~v,~w), attached to the face, in which

the origin is the nose tip, and the axis are the gaze di-

rection, the normal to the face symmetry plane, and

the view up direction. In order to determine the face

pose: we begin by grouping all the points that form

the discrete curves C

determined in the previous sec-

tion, and simply compute their principal axes via the

standard PCA analysis. Since the curves C

inherit the

symmetry property of the facet with respect to face’s

symmetry plane, it is expected that the PCA method

will produce axis that match the face pose to a reason-

ably good extent. In Figure 6.a we depict some exam-

ples of face pose axis plotted on the raw facial scans.

From the face pose, we also derive the face symmetry

plane, having as normal the vector~v and including the

nose tip. Some examples of the symmetry plane are

illustrated in Figure 6(2nd row). We assess the pose

estimation methods in two ways, 1) by aligning pairs

of different face scans of the same individuals using

their estimated poses and 2) by comparing the sym-

metry plane computed by our method with symmetry

plan derived from ground truth data. The ﬁrst experi-

ment was conducted with a group of faces comprising

instances of raw facial scan in neutral expression and

their sad expression counterpart. The facial surface

in this last group are cropped. Figure 6 (3rd and 4th

row) shows some aligned instances. It is clearly ob-

servable that alignments exhibit an acceptable accu-

racy, and thus can be used for a suitable initialization

for the iterative registration algorithms such as the it-

erative closest point method (ICP).

at the nose tip. Figure 5.b shows an instance of 3D

spiral curve spanning the whole face superimposed

on the original surface. This spiral 3D curve encap-

sulates the facial shape variation at a both local and

global scale. Moreover, since the 3D spiral curve is

attached to the facial surface, it can be augmented to

the normal to the face surface at each of points. We

presume that our facial representation spiral facets is

the only model that encode such facial shape varia-

tion into a single mono-dimensional structure. In the

same vein, we construct a 3D closed curve from each

ring in the spiral facets. We obtain a group of con-

centric curves C

,k = 1..N centered at the nose tip.

We can easily control the density of these curves by

a simple subsampling as illustrated in Figure 5.(c).

The

curves inherit from the spiral facet rings the

iso-geodesic property. Therefore they can be used as

low-cost alternative of the iso-gedesic closed curves

employed in (Samir et al., 2009), which do also re-

quire a mesh regularization.

(a) (b)

(c)

Figure 5: a.: A piece of 3D spiral curve emanating from the

nose tip. b: The full spiral curve superimposed on the facial

surface. Facial closed-curves at decreasing sampling rate.

5.4 Face Pose Computation

The computation of the face pose is a critical step to

model based localization and recognition tasks. In

this section, we brief on the details of how our frame-

work is adapted to approximate the face pose of a 3D

facial surface. By face pose, we refer to the coordi-

nate system (O,⃗u,⃗v,⃗w), attached to the face, in which

the origin is the nose tip, and the axis are the gaze di-

rection, the normal to the face symmetry plane, and

the view up direction. In order to determine the face

pose: we begin by grouping all the points that form

the discrete curves C

determined in the previous sec-

tion, and simply compute their principal axes via the

standard PCA analysis. Since the curves C

inherit the

symmetry property of the facet with respect to face’s

symmetry plane, it is expected that the PCA method

will produce axis that match the face pose to a reason-

ably good extent. In Figure 6.a we depict some exam-

ples of face pose axis plotted on the raw facial scans.

From the face pose, we also derive the face symmetry

plane, having as normal the vector⃗v and including the

nose tip. Some examples of the symmetry plane are

illustrated in Figure 6(2nd row). We assess the pose

estimation methods in two ways, 1) by aligning pairs

of different face scans of the same individuals using

their estimated poses and 2) by comparing the sym-

metry plane computed by our method with symmetry

plan derived from ground truth data. The ﬁrst experi-

ment was conducted with a group of faces comprising

instances of raw facial scan in neutral expression and

their sad expression counterpart. The facial surface

in this last group are cropped. Figure 6 (3rd and 4th

row) shows some aligned instances. It is clearly ob-

servable that alignments exhibit an acceptable accu-

racy, and thus can be used for a suitable initialization

for the iterative registration algorithms such as the it-

erative closest point method (ICP).

Figure 6: Computation of the face pose (1st row) and deduc-

tion of the face symmetry plane for some face samples (2nd

row). 3rd and 4rth rows:Alignment of cropped instances of

faces exhibiting sad facial expression to their counterparts

raw images in a neutral expressions.

In the second method of assessment, we consider

symmetry plane estimation error as the angle between

the the two normals of the estimated and the actual

planes. We computed the estimation error for a group

of 200 3D face instances (100 neutrals and 100 sads)

and have found a standard deviation error of 2 degree

for a mean error of 0.03 degree, and a maximum error

of 4 degree.

In addition, we also assess the stability of the

Figure 6: Computation of the face pose (1st row) and deduc-

tion of the face symmetry plane for some face samples (2nd

row). 3rd and 4rth rows:Alignment of cropped instances of

faces exhibiting sad facial expression to their counterparts

raw images in a neutral expressions.

In the second method of assessment, we consider

symmetry plane estimation error as the angle between

the the two normals of the estimated and the actual

planes. We computed the estimation error for a group

of 200 3D face instances (100 neutrals and 100 sads)

and have found a standard deviation error of 2 degree

for a mean error of 0.03 degree, and a maximum error

of 4 degree.

In addition, we also assess the stability of the face

pose estimate against increasing number of rings that

deﬁne the faceprint. Here, we consider 100 sample

images, 56 female and 44 male subjects at neutral po-

sitions. For each sample, we compute the face orien-

tation for increasing percentages of the number rings

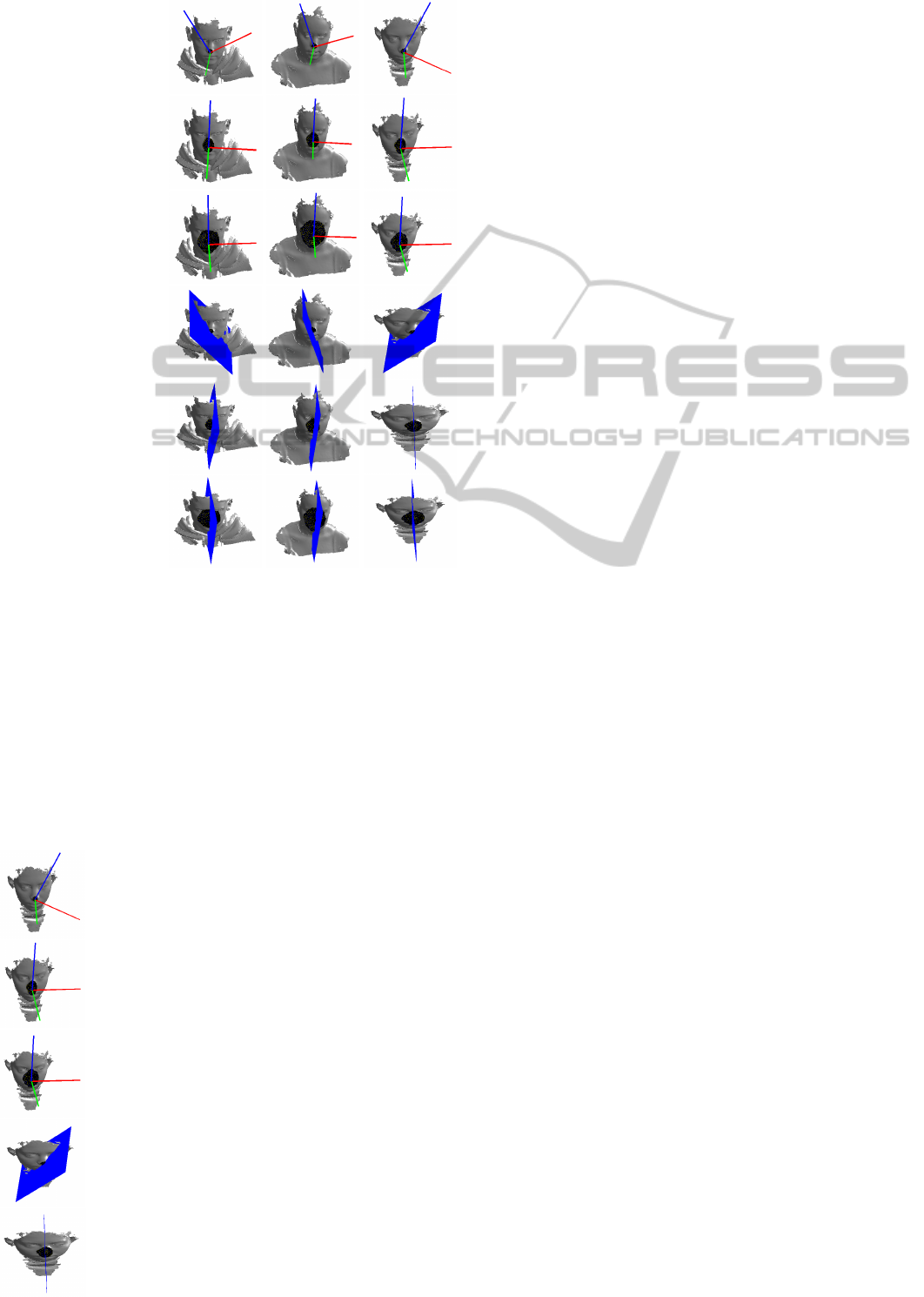
starting 10% to 90% in steps of 20%. In Figure 7, we

illustrate sample results of the aforementioned exper-

iment. Rows 1 to 3 depict the face orientation with

30%, 50% and 70% of the maximum number rings

and rows 4 to 6 shows the corresponding symmetry

planes for different face samples (columns). As we

can visually notice, the face pose stabilizes nearly at

50% of the maximum number of rings that is required

to describe the facial surface.

To further probe the issue of the stability of face

pose, we construct histograms of the percentage of

number of face images that exhibit stable face orien-

tation against increasing percentage of the number of

rings on distinguished male and female subjects as in

Figure 8. We measure stability in face pose as the

difference in the angular distance between consecu-

tive face pose estimates with increasing rings being

lesser than a predeﬁned threshold (which is 0.15 in

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

face pose estimate against increasing number of

rings that deﬁne the faceprint. Here, we consider

100 sample images, 56 female and 44 male subjects

at neutral positions. For each sample, we compute

the face orientation for increasing percentages of

the number rings starting 10% to 90% in steps of

20%. In Figure 7, we illustrate sample results of

the aforementioned experiment. Rows 1 to 3 depict

the face orientation with 30%, 50% and 70% of the

maximum number rings and rows 4 to 6 shows the

corresponding symmetry planes for different face

samples (columns). As we can visually notice, the

face pose stabilizes nearly at 50% of the maximum

number of rings that is required to describe the facial

surface.

Figure 7: Stability of the face pose (1-3 columns) and the

corresponding face symmetry plane (4-6 columns) with in-

creasing number of rings (20% rise) on different face sam-

ples (columns)

To further probe the issue of the stability of face

pose, we construct histograms of the percentage of

number of face images that exhibit stable face orien-

tation against increasing percentage of the number of

rings on distinguished male and female subjects as in

Figure 8. We measure stability in face pose as the

difference in the angular distance between consecu-

tive face pose estimates with increasing rings being

lesser than a predeﬁned threshold (which is 0.15 in

our case). It is clear that over 92% of samples need

just 70% of the maximum rings to produce stable face

orientations and nearly 60% of samples need 50% of

the maximum rings to produce stable face pose esti-

mates.

Figure 8: Percentage of face with stabilized face orienta-

tion (y-axis) versus the percentage increase in the number

of rings across male (blue) and female (yellow) samples

5.5 Nose Proﬁle Identiﬁcation

As the ﬁnal application of the spiral facets framework,

we describe the problem of nose proﬁle identiﬁcation.

We deﬁne the nose proﬁle as a curve that joins the

nose bridge with the nose tip across the face plane of

symmetry. This curve follows the path of high cur-

vature along the nose, which nearly coincides with

shortest path between these two points. We extend

our framework based on geodesic paths as described

at the end of 4 to identify the nose proﬁle. In effect,

at it is shown in Figure 1.f, geodesic paths that join

neighboring facets, in a given ring of the facet spiral,

to the nose tip, get merged into a common path. This

applies particularly for paths emanating at the cen-

tral forehead where we can clearly observe the con-

vergence of the paths at some level of the nose pro-

ﬁle. We draw inspiration from this observation and

use a frequency histogram that accumulates the occur-

rences of the facets at each path. The entries of this

histogram include all the facets crossed by the paths.

Based on this, we propose a nose proﬁle detection

method composed of the following steps: In a ﬁrst

Figure 7: Stability of the face pose (1-3 columns) and the

corresponding face symmetry plane (4-6 columns) with in-

creasing number of rings (20% rise) on different face sam-

ples (columns).

our case). It is clear that over 92% of samples need

just 70% of the maximum rings to produce stable face

orientations and nearly 60% of samples need 50% of

the maximum rings to produce stable face pose esti-

mates.

face pose estimate against increasing number of

rings that deﬁne the faceprint. Here, we consider

100 sample images, 56 female and 44 male subjects

at neutral positions. For each sample, we compute

the face orientation for increasing percentages of

the number rings starting 10% to 90% in steps of

20%. In Figure 7, we illustrate sample results of

the aforementioned experiment. Rows 1 to 3 depict

the face orientation with 30%, 50% and 70% of the

maximum number rings and rows 4 to 6 shows the

corresponding symmetry planes for different face

samples (columns). As we can visually notice, the

face pose stabilizes nearly at 50% of the maximum

number of rings that is required to describe the facial

surface.

Figure 7: Stability of the face pose (1-3 columns) and the

corresponding face symmetry plane (4-6 columns) with in-

creasing number of rings (20% rise) on different face sam-

ples (columns)

To further probe the issue of the stability of face

pose, we construct histograms of the percentage of

number of face images that exhibit stable face orien-

tation against increasing percentage of the number of

rings on distinguished male and female subjects as in

Figure 8. We measure stability in face pose as the

difference in the angular distance between consecu-

tive face pose estimates with increasing rings being

lesser than a predeﬁned threshold (which is 0.15 in

our case). It is clear that over 92% of samples need

just 70% of the maximum rings to produce stable face

orientations and nearly 60% of samples need 50% of

the maximum rings to produce stable face pose esti-

mates.

Figure 8: Percentage of face with stabilized face orienta-

tion (y-axis) versus the percentage increase in the number

of rings across male (blue) and female (yellow) samples

5.5 Nose Proﬁle Identiﬁcation

As the ﬁnal application of the spiral facets framework,

we describe the problem of nose proﬁle identiﬁcation.

We deﬁne the nose proﬁle as a curve that joins the

nose bridge with the nose tip across the face plane of

symmetry. This curve follows the path of high cur-

vature along the nose, which nearly coincides with

shortest path between these two points. We extend

our framework based on geodesic paths as described

at the end of 4 to identify the nose proﬁle. In effect,

at it is shown in Figure 1.f, geodesic paths that join

neighboring facets, in a given ring of the facet spiral,

to the nose tip, get merged into a common path. This

applies particularly for paths emanating at the cen-

tral forehead where we can clearly observe the con-

vergence of the paths at some level of the nose pro-

ﬁle. We draw inspiration from this observation and

use a frequency histogram that accumulates the occur-

rences of the facets at each path. The entries of this

histogram include all the facets crossed by the paths.

Based on this, we propose a nose proﬁle detection

method composed of the following steps: In a ﬁrst

Figure 8: Percentage of face with stabilized face orienta-

tion (y-axis) versus the percentage increase in the number

of rings across male (blue) and female (yellow) samples.

5.5 Nose Proﬁle Identiﬁcation

As the ﬁnal application of the spiral facets framework,

we describe the problem of nose proﬁle identiﬁcation.

We deﬁne the nose proﬁle as a curve that joins the

nose bridge with the nose tip across the face plane of

symmetry. This curve follows the path of high cur-

vature along the nose, which nearly coincides with

shortest path between these two points. We extend

our framework based on geodesic paths as described

at the end of 4 to identify the nose proﬁle. In effect,

at it is shown in Figure 1.f, geodesic paths that join

neighboring facets, in a given ring of the facet spiral,

to the nose tip, get merged into a common path. This

applies particularly for paths emanating at the cen-

tral forehead where we can clearly observe the con-

vergence of the paths at some level of the nose pro-

ﬁle. We draw inspiration from this observation and

use a frequency histogram that accumulates the occur-

rences of the facets at each path. The entries of this

histogram include all the facets crossed by the paths.

Based on this, we propose a nose proﬁle detection

method composed of the following steps: In a ﬁrst

step we select a ring R that passes through the fore-

head, which generally corresponds the last few rings,

however in order to avoid border effects we choose

the third ring from the last one as illustrated in (Fig-

ure 9.a). The chosen ring R intersects the symmetry

plane at two points within two facets located at the

forehead and chin areas. We then extract a portion

of the ring R keeping the selected facets as the me-

dian as shown in Figure 9.b. In the third step, we

generate a group of geodesic paths converging to the

nose tip. These paths are represented by sequences

of facets joining the two strips to the nose tip (Fig-

ure 9.c). From the two groups of facet sequences S

and S

we built two histograms that encodes the dis-

tribution of the facets across these paths (Figure 9.d).

From each histogram we extract the two groups of

facets having a score above a certain threshold (Fig-

ure 9.e) and in order to to select the valid group of

facets; we perform a 3D line ﬁtting to the facets’ ver-

tices in each group (Figure 9.f). Finally, we choose

the line producing the least residual error (Figure 9.g)

to correspond to the nose proﬁle. Figure 9.h depicts

some examples of detected nose proﬁles.

6 CONCLUSIONS AND FUTURE

WORK

In this work, we presented a uniﬁed framework for

analyzing and describing 3D facial surface. Our rep-

resentation of 3D facial surface using spiral facets has

THE SPIRAL FACETS - A Unified Framework for the Analysis and Description of 3D Facial Mesh Surfaces

step we select a ring R that passes through the fore-

head, which generally corresponds the last few rings,

however in order to avoid border effects we choose

the third ring from the last one as illustrated in (Fig-

ure 9.a). The chosen ring R intersects the symmetry

plane at two points within two facets located at the

forehead and chin areas. We then extract a portion

of the ring R keeping the selected facets as the me-

dian as shown in Figure 9.b. In the third step, we

generate a group of geodesic paths converging to the

nose tip. These paths are represented by sequences

of facets joining the two strips to the nose tip (Fig-

ure 9.c). From the two groups of facet sequences S

and S

we built two histograms that encodes the dis-

tribution of the facets across these paths (Figure 9.d).

From each histogram we extract the two groups of

facets having a score above a certain threshold (Fig-

ure 9.e) and in order to to select the valid group of

facets; we perform a 3D line ﬁtting to the facets’ ver-

tices in each group (Figure 9.f). Finally, we choose

the line producing the least residual error (Figure 9.g)

to correspond to the nose proﬁle. Figure 9.h depicts

some examples of detected nose proﬁles.

(a) (b) (c) (d)

(e) (f) (g)

(h)

Figure 9: Nose proﬁle detection. a: Selection of a facet

rings. b:Intersection with the approximate estimation of the

symmetry plane Γ and generation of two stripes. c: Ex-

traction of sequences of facets following the geodesic paths

from the two stripes. to the nose tip. d: For each a group,

a geometric histogram is computed to select facets scoring

large occurrences. e: The two candidate groups of facets (in

blue and yellow in colored images). f: 3D line ﬁtting of two

groups of facets and selection of the one having the lowest

residual error. g: Display of the valid line passing the nose

proﬁle.h: Examples of detected nose proﬁles.

6 Conclusions and Future Work

In this work, we presented a uniﬁed framework for

analyzing and describing 3D facial surface. Our rep-

resentation of 3D facial surface using spiral facets has

resulted in a mechanism that is intrinsic to the face

surface, more simple, compact, generic and compu-

tationally less expensive than other popular represen-

tations. The facet spiral has wide spectrum of appli-

cation that include nose tip detection, frontal face ex-

traction, face shape description, face pose computa-

tion and nose proﬁle identiﬁcation. In the future, we

plan to explore more deeply the facial shape descrip-

tion aspect. In this context, we plan to investigate how

we can derive from the spiral curves and the concen-

tric close curves, a kind of a ”faceprint” that would

uniquely deﬁne the face. We plan also to investigate

further the compactness aspect of the facet spiral, the

spiral-wise ordering of the facets and the topological

constraints in a the facet spiral can exploited to de-

rive a one-dimensional compressed model of the fa-

cial surface.

REFERENCES

Ashbrook, A. P., Fisher, R. B., Robertson, C., and Werghi,

N. (1998). Finding surface correspondance for object

recognition and registration using pairwise geometric

histograms. In Proc European Conference on Com-

puter Vision, pages 674–686.

Berretti, S., Bimbo, A., and Pala, P. (2006). Description and

retrieval of 3d face models using iso-geodesic stripes.

In In Conf. Multimedia Information Retrieval, page

1322.

Bronstein, A., Bronstein, M., and Kimmel, R. (2003). Ex-

pression invariant 3d face recognition. Audio- and

Video-Based Person Authentication, pages 62–70.

Chua, C., Han, F., and Ho, Y. (2000). 3d human face recog-

nition using point signature. In In Conf. on Automatic

Face and Gesture Recognition, pages 233–238.

Colbry, D., Stockman, G., and Jain, A. (2005). Detection of

anchor points for 3d face veriﬁcation. In Proc. Com-

puter Vision and Pattern Recognition.

Cormen, T. H., Leiserson, C., Rivest, R. L., and Stein., C.

(2001). Introduction to Algorithms, Second Edition.

MIT Press and McGraw-Hill.

F.R., A.-O., Bennamoun, M., and Mian, A. (2008). Integra-

tion of local and global geometrical cues for 3d face

recognition. Pattern Recognition, 41(3):1030–1040.

Frey, P. and Borouchaki, H. (1999). Surface mesh qual-

ity evaluation. International Journal for Numerical

Methods in Engineering, 45(1):101–118.

Heseltine, T., Pears, N., and Austin, J. (2008). Three-

dimensional face recognition using combinations of

Figure 9: Nose proﬁle detection. a: Selection of a facet

rings. b:Intersection with the approximate estimation of the

symmetry plane Γ and generation of two stripes. c: Ex-

traction of sequences of facets following the geodesic paths

from the two stripes. to the nose tip. d: For each a group,

a geometric histogram is computed to select facets scoring

large occurrences. e: The two candidate groups of facets (in

blue and yellow in colored images). f: 3D line ﬁtting of two

groups of facets and selection of the one having the lowest

residual error. g: Display of the valid line passing the nose

proﬁle.h: Examples of detected nose proﬁles.

resulted in a mechanism that is intrinsic to the face

surface, more simple, compact, generic and compu-

tationally less expensive than other popular represen-

tations. The facet spiral has wide spectrum of appli-

cation that include nose tip detection, frontal face ex-

traction, face shape description, face pose computa-

tion and nose proﬁle identiﬁcation. In the future, we

plan to explore more deeply the facial shape descrip-

tion aspect. In this context, we plan to investigate how

we can derive from the spiral curves and the concen-

tric close curves, a kind of a ”faceprint” that would

uniquely deﬁne the face. We plan also to investigate

further the compactness aspect of the facet spiral, the

spiral-wise ordering of the facets and the topological

constraints in a the facet spiral can exploited to de-

rive a one-dimensional compressed model of the fa-

cial surface.

REFERENCES

Ashbrook, A. P., Fisher, R. B., Robertson, C., and Werghi,

N.(1998). Finding surface correspondance for object

recognition and registration using pairwise geometric

histograms. In Proc European Conference on Com-

puter Vision, pages 674686.

Berretti, S., Bimbo, A. and Pala, P.(2006). Description

and retrieval of 3D face models using iso-geodesic

stripes. In Conf. Multimedia Information Retrieval,

page 1322.

Bronstein, A., Bronstein, M. and Kimmel, R.(2003). Ex-

pression invariant 3D face recognition. Audio-and

Video-based Person Authentication, pages 6270.

Chua, C., Han, F. and Ho, Y.(2000). 3D Human face recog-

nition using point signature. In Conf. on Automatic

Face and Gesture Recognition, pages 233238.

Colbry, D., Stockman, G. and Jain, A.(2005). Detec-

tion of anchor points for 3D face veriﬁcation. In

Proc.Computer Vision and Pattern Recognition.

Cormen, T. H., Leiserson, C., Rivest, R. L. and Stein.,

C.(2001). Introduction to Algorithms, Second Edition.

MIT Pressand McGraw-Hill.

F. R., A.-O., Bennamoun, M. and Mian, A.(2008). Integra-

tion of local and global geometrical cues for 3D face

recognition. Pattern Recognition, 41(3):10301040

Frey, P. and Borouchaki, H.(1999). Surface mesh qual-

ity evaluation. International Journal for Numerical

Methods in Engineering,45(1):101118.

Heseltine, T., Pears, N. and Austin, J.(2008). Three-

dimensional face recognition using combinations of

surface feature map subspace components. Image and

Vision Computing, 26:382-396

Irfanoglu, M., Gokberk, B. and Akarun, L.(2004). 3D

shape-based face recognition using automatically reg-

istered facial surfaces. In Conf. Pattern Recognition,

volume4, pages 183186.

Kakadiaris, I.(2007). Three-dimensional face recognition in

the presence of facial expressions: An annotated de-

formable model approach. IEEE Transaction on Pat-

tern Analysis and Machine Intelligence,29(4).

Lee, Y., Park, K., Shim, J. and Yi, T.(2003). 3D face recog-

nition using statistical multiple features for the local

depth information. In Conf. Vision Interface, pages

102108.

Lu, X. and Jain, A.(2005). Deformation analysis for 3D

face matching. In IEEE Workshops on Application of

Computer Vision, pages 99104.

Mian, A., Bennamoun, M. and Owens, R.(2007). An efﬁ-

cient multimodal 2D-3D hybrid approach to automatic

face recognition. IEEE Transactions in Pattern Anal-

ysis and Machine Intelligence, 29(11):19271943.

Moreno, A., Sanchez, A. and Martinez, E.(2006). Robust

representation of 3D faces for recognition. Int. Jour-

nal of Pattern Recognition and Artiﬁcial Intelligence,

20(8):11591186.

Nair, P. and Cavallaro, A.(2009) 3-d face detection,land-

mark localization, and registration using a point distri-

bution model. IEEE Trans. Multimedia, 1(4):611623.

Pan, G., Wu, Y., Wu, Z. and Liu, W.(2003). 3D face recog-

nition by proﬁle and surface matching. In IEEE/INNS

Conf. on Neural Networks, volume3, pages 21692174.

Piegl, L. and Tiller, W.(2006) The NURBS Book. Springer.

R. Niese, Al-Hamadi, A. and Michaelsi, B.(2007) A novel

method for 3D face detection and normalization. Jour-

nal of Multimedia,2(5):112.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

Romero, M. and Pears, N.(2009). Landmark localisation in

3D face data. In IEEE Conf. on Advanced Video and

Signal Based Surveillance, pages 7378.

Ruiz, M. and Illingworth,J.(2008). Automatic landmark-

ing of faces in 3D-alf. In 5th International Confer-

ence on Visual Information Engineering(VIE2008),

pages4146.

Samir, C., Srivastava, A., Daoudi, M. and Klassen, E.

(2009) An intrinsic framework for Analysis of facial

surfaces. International Journal of Computer Vision,

82(1).

Segundo, M., Queirolo, C., Bellon,O. and Silva, L.(2007).

Automatic 3D facial segmentation and landmark de-

tection. In Proc. 14th Int.Conf. on Image Analysis and

Processing, page431436.

Sethian, J. and Kimmel., R.(1998). Computing geodesic

paths on manifolds. Proc. National Academy of Sci-

ences, 95(15):84318435.

Wang, Y., Tang, X., Liu, J., Pan, G. and Xiao, R.(2008). 3D

face recognition by local shape difference boosting.

In Proc. European Conference on Computer Vision,

ECCV, pages 603616.

Wu, Y., Pan, G. and Wu, Z.(2003). Face authentication

based on multiple proﬁles extracted from range data.

In Conf. Audio-and Video-Based Biometric Person

Authentication, volume 2688, pages 515522.

Xu, C., Tan, T., Wang, Y. and Quan, L.(2006) Combin-

ing local features for robust nose location in 3D facial

data. Pattern Recognition Letters, 27:14871494.

Xu, C., Wang, Y., Tan, T. and Quan, L.(2004a). Automatic

3D face recognition combining global geometric fea-

tures with local shape variation information. In IEEE

Conf. on Automatic Face and Gesture Recognition,

pages 302307.

Xu, C., Wang, Y., Tan, T. and Quan, L.(2004b) A new at-

tempt to face recognition using eigenfaces. In Asian

Conference on Computer Vision, volume 2, pages

884889.

Xu, D., Hu, P., Cao, W. and Li, H.(2008). 3D face recog-

nition using moment in variants. In IEEE Int. Con-

ference on Shape Modeling and Applications, pages

261262.

THE SPIRAL FACETS - A Unified Framework for the Analysis and Description of 3D Facial Mesh Surfaces