FAST TEMPLATE MATCHING FOR UMTS CODE KEYS

WITH GRAPHICS HARDWARE

Mario Vigliar, Giancarlo Raiconi

DMI, Universit

a degli Studi di Salerno, via Ponte don Melillo, 84083, Fisciano SA, Italy

Alan David Sanders

Wider Networks, 881 Ponce de Leon Ave Suite 10, 30306 Atlanta GA, U.S.A.

Keywords:

Measurements on 3G networks, GPU computation, FFT.

Abstract:

Template matching is a milestone application in Digital Signal Processing, and sets its roots in fundamental

numeric ﬁltering theory, as well as in time and frequency domain analysis. Radio signals, with mass spreading

of high bandwidth cellular networks, have become in recent years much more critical to handle in terms of

QoS (Quality of Service), QoE (Quality of Experience) and SLA (Service Level Agreement), putting mobile

carriers in the need to monitor their network status in a more detailed and efﬁcient way than in past. Here

an efﬁcient use case of GPU computing applied to fast signal processing will be illustrated, with particular

interest in study and development of a SIMD Linear and FFT-based cross correlation of multiple code keys in

air-captured streams for UMTS networks. Developed techniques have been used with success in a commercial

available 3G geotagged scanning equipment.

1 INTRODUCTION

The aim of this paper is to present a parallel comput-

ing approach to solve the problem of precisely mea-

sure the maximal exposure to UMTS (Universal Mo-

bile Telecommunications System) signals in an area.

Because the particular nature of this signal character-

ized by a high crest factor such task cannot be sim-

ply carried out by a ﬁeld intensity meter but the only

means consists in really receive the signal by an ap-

propriate receiver and evaluate the signal quality.

Traditionally to this purpose, which is a computa-

tionally intensive task, the receiver was mounted on a

vehicle, the received signal was recorded and used to

signal exposition evaluation carried out ofﬂine. Such

approach result on a set of costly operations in terms

of time spent and specialized components used. Our

approach consist of direct computation of necessary

data directly onboard using a standard laptop, costly

signal processing operation are performed efﬁciently

exploiting the power of a standard GPU of the laptop

using NVidia’s CUDA framework.

The paper is organized as follows. In the next sec-

tion the problem is stated by as template matching

problem, solvable using classical Digital Signal Pro-

cessing (DSP) technique in order to compute the cross

correlation between sequences. the third section is

devoted to describe the computational technique im-

plemented in the Wider Network’s scanner based on

a specialized FFT algorithm running on GPU. In the

following section the computational aspects of the al-

gorithm are studied in detail and results of benchmark

are reported.

Finally there is a concluding section.

2 PROBLEM STATEMENT

In this section we recall brieﬂy relevant features of the

UMTS signal and describe what computational tasks

need to perform in order to assess the quality of the

signal itself.

2.1 A Brief Sketch of the UMTS Signal

To understand the algorithm which is used to evaluate

UMTS signal quality the knowledge of some details

of its characterization are necessary. UMTS uses a

multiple access technique, where several users as well

as the signalization is separated by different spreading

265

Vigliar M., Raiconi G. and David Sanders A..

FAST TEMPLATE MATCHING FOR UMTS CODE KEYS WITH GRAPHICS HARDWARE.

DOI: 10.5220/0003362902650272

In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2011), pages

265-272

ISBN: 978-989-8425-48-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

codes (WCDMA - Wideband Code Division Multiple

Access). By multiplication with the spreading code,

the data signal is spread in the spectrum. Fig. 1a

taken from (Bornkessel and Wuschek, 2006) shows

a real measured UMTS signal in frequency domain.

The 10 dB bandwidth is about 4.3 MHz. UMTS sig-

nals are noise like showing a large difference between

short time maxima U

Peak

and the RMS value U

RMS

(crest factor C = 20 · log(U

Peak

RMS

) in the 8 to 10

dB range, variable with the trafﬁc of the station).

(a)

(b)

Figure 1: UMTS signal spectrum and its analysis with

WIND3G.

In order to determine the maximal exposure in

a deﬁned volume, the sweeping method is recom-

mended, due to signal nature. Common Pilot Channel

(CPICH) is a ﬁxed rate (30 kbps, Spreading Factor

- SF=256) downlink physical channel that carries a

pre-deﬁned bit sequence. Figure 2 shows the frame

structure of the CPICH. The Primary CPICH is

used by the UEs (user equipments) to ﬁrst complete

identiﬁcation of the Primary Scrambling Code used

for scrambling Primary Common Control Physical

Channel (P-CCPCH) transmissions from the Node

B (in UMTS is the Base Transceiver Station). Later

CPICH channels provide allow phase and power

estimations to be made, as well as aiding discovery

of other radio paths. There is one primary CPICH (P-

CPICH), which is transmitted using spreading code 0

with a spreading factor of 256, notationally written as

ch,256,0

. Optionally a Node B may broadcast one or

more secondary common pilot channels (S-CPICH),

which use 256 codes arbitrarily chosen, written as

ch,256,n

where 0 < n < 256. The CPICH contains

20 bits of data, which are either all zeros, or in the

case that Space-Time Transmit Diversity (STTD)

is employed, is a pattern of alternating 1’s and 0’s

for transmissions on the Node B’s second antenna.

The ﬁrst antenna of a base station always transmits

all zeros for CPICH. See below for P-CPICH and

S-CPICH characterization.

Figure 2: Frame structure and modulation pattern for

Common Pilot Channel.

In case transmit diversity is used on P-CCPCH

and SCH, the CPICH shall be transmitted from both

antennas using the same channelization and scram-

bling code. In this case, the pre-deﬁned bit sequence

of the CPICH is different for Antenna 1 and Antenna

2, see ﬁgure 2 (top section). In case of no transmit

diversity, only the bit sequence of Antenna 1 is used.

The channelization codes are the same codes as

used in the up-link, namely Orthogonal Variable

Spreading Factor (OVSF) codes that preserve the or-

thogonality between downlink channels of different

rates and spreading factors. The channelization code

for the Primary CPICH is ﬁxed to C

ch,256,0

as previ-

ously stated, and the channelization code for the Pri-

mary CCPCH is ﬁxed to C

ch,256,1

. In each cell the UE

may be conﬁgured simultaneously with at most two

scrambling codes. The scrambling code sequences

are constructed by combining two real sequences into

a complex sequence. Each of the two real sequences

are constructed as the position wise modulo 2 sum of

38400 chip segments of two binary m-sequences gen-

erated by means of two generator polynomials of de-

gree 18. The resulting sequences thus constitute seg-

ments of a set of Gold sequences.

The scrambling codes are repeated for every 10

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

266

ms radio frame. Let x and y be the two sequences

respectively. The x sequence is constructed using the

primitive (over GF(2)) polynomial 1+X

. The

y sequence is constructed using the polynomial 1 +

+ X

2.2 Monitoring and Mapping UMTS

Signal Quality

Our main interest is in “measurement for perfor-

mances” and so our main aim will be to decode air-

captured data to evaluate if it is possible to decode

some subsequences in useful cell broadcasting pack-

ets. As signal matching measure was used cross cor-

relation:

( f ? g)[n]

def

∞

∑

m=−∞

∗

[m] g[n +m]. (1)

for a ﬁxed n, in the interval [0...n] it is possible to

compute the single terms of sum sequence just iterat-

ing the product between f

∗

and g terms. For each iter-

ation, a single correlation value will be obtained, and

ﬁnding a local maxima will indicate the best match

position in the search reference of the candidate se-

quence. This computing method is often referred

as linear cross-correlation index, and used in online

systems when seeking for short length templates in

streaming references, due to overall small memory

footprint and good independency from ﬂoating point

precision on the target architecture. Linear cross-corr.

in fact, relies only on sum and multiply operations,

thus ensuring very good computing performances on

DSP-like systems, where MADD (Multiply and AD-

Dition) primitives are present in hardware, and often

within vectorial structures.

Let x,y two sequences and X, Y their Fourier

transforms it can be shown that:

−1

{

∗

· Y

}

N−1

∑

l=0

∗

·(y

)

n+l

def

= (x ? y

)

, (2)

which is the cross correlation of the x sequence

with a periodically extended y sequence deﬁned by:

)

def

∞

∑

p=−∞

(n−pN)

. (3)

This formulation is often referred as circular correla-

tion. Efﬁcient implementations of Fourier transform

on PoT-length (Power of Two) sequences, like FFT

in its many ﬂavors, offer us the chance to lower the

O(n

) complexity bound of linear correlation, to im-

prove performances in terms of no. of possible tem-

plates checkable for time unit (samples/secs).

3 WIDER NETWORKS CASE

STUDY

Wider Networks’ UMTS scanner (WIND3G - Figure

1b) has an CPICH Ec/Io

detection of -25 dB. Lower

Ec/Io detection comes from increased signal process-

ing power.

Given a ﬁxed number of CPICH chips as tem-

plates, the lower is the requested Ec/Io ratio (to avoid

misdetections) the more processing power is needed.

Samples’ length is another key point when evaluating

the real computational complexity of the process, as

linear correlation needs to evaluate the signal ﬁtness

on the whole target sequence. See Figure 3 to better

understand the detection thresholds in the seek pro-

cess.

We are aimed to improve timing for full cross

correlation between air-captured streams and a given

number of ﬁlters (512 scrambling codes for ﬁrst

stage), starting from a vectorized version of lin-

ear cross correlation (provided in Intel Performance

Primitives libraries). Actual routines were running

in SSE2 cores, ﬂoating point single precision IEEE-

754 32 bits, and were multicore aware. There are

512 CPICH scrambling code sequences in UMTS.

WIND3G takes about 3580 chips worth of each and

correlates against one complete UMTS frame, which

is 38400 chips to ﬁnd where these CPICHs have

peaks. This step is called “Searching code”, and it

is actually target of these performance benchmarks.

After searching the peak, a DSP algorithm called

Tracker takes it in charge to monitor variations over

time. Theoretical compound performances of the

Searcher+Tracker modules have a bottom limit of

25.5 dB. A peak with this magnitude (and lower) has

a considerable probability of being a false detection.

Wider Networks’ system are designed to work

in mobile environments (cars, service vans) as the

UMTS scanner is bundled with a GPS receiver and

a geotagging application, to write down on updated

maps the dB values, signal efﬁciency and other mea-

surements done when roaming across cell network

covered area. For this reason, their main comput-

ing unit is often a notebook, and so with no particular

and/or optimized processor for signal processing (up

to 2 cores, no SMP, no expansion slots for accelera-

tors, frequencies up to 2.5 GHz due to thermal and

power issues).

To overcome to these performance limits, a fast

circular cross correlator has been designed to run in

GPU, and most notably on NVidia GeForce 8xxx

In UMTS/CDMA Ec/Io refers to the portion of the RF

signal which is usable. It’s the difference between the signal

strength and the noise ﬂoor.

FAST TEMPLATE MATCHING FOR UMTS CODE KEYS WITH GRAPHICS HARDWARE

267

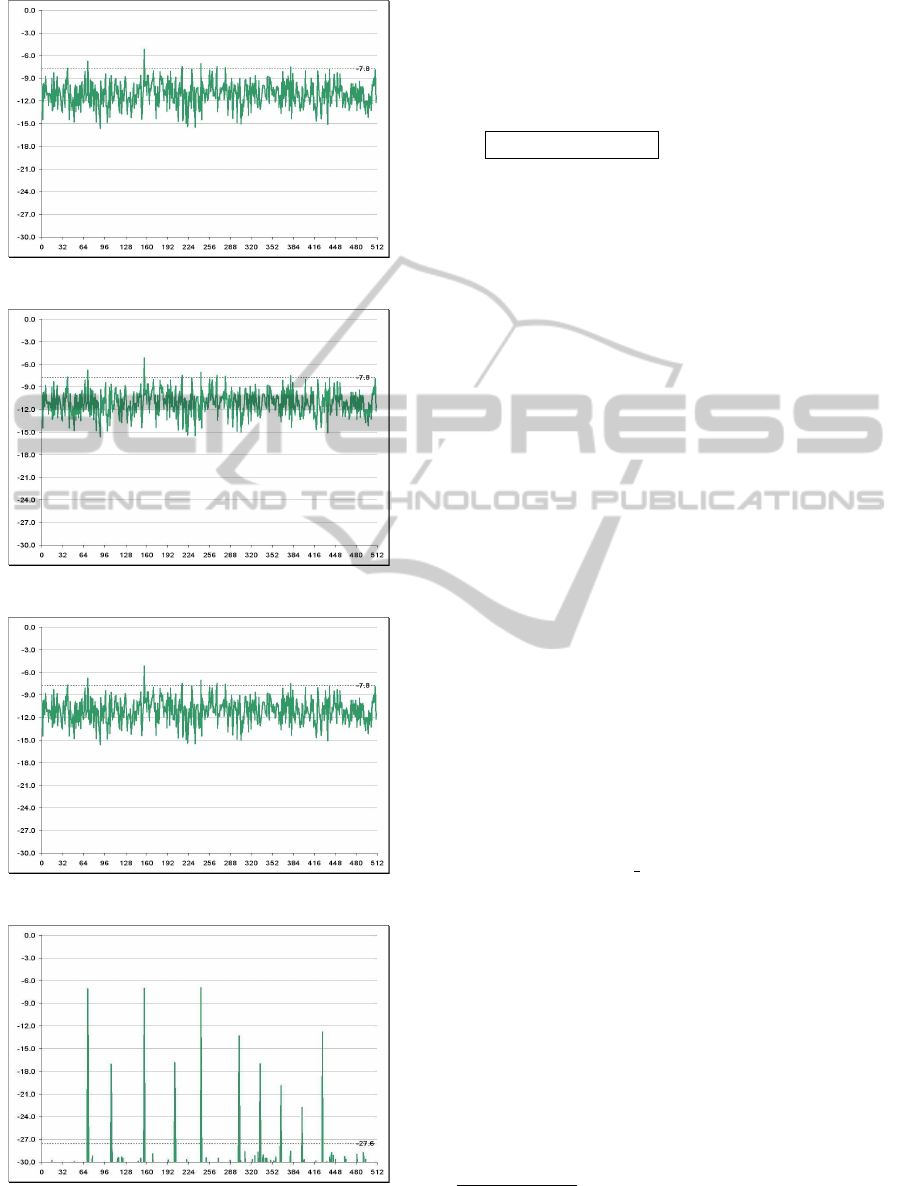
(a) -7.9 dB.

(b) -16.6 dB.

(d) -27.6 dB.

Figure 3: CPICH Ec/Io detection thresholds.

chipsets and newer, by using CUDA development

framework under Windows XP (both 32 and 64 bits).

The OS choice was mandatory to minimize porting

efforts of the whole WIND3G application, already

available for that system.

UMTS Cell Search

• Cell Search by correlating CPICH associated with

all 512 scrambling codes (α-search)

• In fast-mode (β-search) speciﬁed top few candi-

dates (sample positions) are correlated

1. Find the maximum correlation value for each

scrambling code → 512 max values (run code

in 1)

2. Sort these 512 max values, pick the top k scr.

codes (because the maximums of the rest scr.

codes will be anyway discarded later)

3. For each of these k scr-codes, sort their corre-

lation values for all positions disregarding the

values within +/-2 chips of a local max, and

pick the top j or so positions → In total, this

will give us k ∗ j initial candidates

4. Sort the k ∗ j candidates to ﬁnd the ﬁnal m can-

didates to β-search.

Running system use this setup: k = 200, j =

10, m = 200. Values have been tested on ﬁeld and

provide satisfactory results for detection.

3.1 Circular Cross Correlation with

CUDA

Once tested the IPP

cross correlation code, strictly

optimized for x86 platforms, an ofﬂoaded routine

moving part of the computing costs in GPU is pro-

posed here. See Listing 1 for a signiﬁcant snippet

from cudaCrossCorr 32fc.

Listing above requires some explanations for

some critical and interesting points. Firstly, this

CUDA code is totally “masked” (with singular excep-

tion at line 21), keeping reading and maintenance as

easy as for plain C/C++ source code. Thanks to mod-

ular CUFFT structure derived from FFTW library it

has been possible in fact to remove any direct kernel

invocation and substitute 1:1 the IPP calls in this al-

gorithm.

Remarkable point is moreover the stateful nature

of cross corr. code. A major drawback of circular

correlation vs. linear one, especially if built up to have

exactly the same external interface, would have been

Intel

 Integrated Performance Primitives - see

http://software.intel.com/en-us/articles/intel-ipp/ for further

information.

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

268

Listing 1: cudaCrossCorr 32fc source.

extern "C" void

cu daC ros sCo rr_ 32f c ( Co mp le x * h_ fi lt er _k er ne l ,

int fil te rS i ze , \

Co mp le x * h_s i gn al , int si gn al S iz e , \

Co mp le x * h_ co r r _ s i g n a l , int c or rSi ze , \

int lowLa g , bool si gn FF T e d )

{

// Pad signal and filter kernel

Co mp le x * h_ pa dd ed _s ig na l , h _ pa d de d _f i lt e r_ k er n e l ;

[. . .]

// Transform signal and kernel

if (! s i g n FF Te d ) {

cu f f t Ex e c C 2C ( plan , ( c u ff t C o mp l e x *) d_ s ig nal , \

( c uf f tC om p le x *) d _s i gn al , C UF F T _ FO R W A RD ) ;

}

cu f f t Ex e c C 2C ( plan , ( c u ff t C o mp l e x *) d _ f i l t e r_ ke rn el , \

( c uf f tC om p le x *) d_ fi lt er _k er ne l , C U F F T_ F O R WA R D ) ;

// Multiply coefficients together as in corr a.

conj(b)

Co m p l ex C on j P o i n t wi s eM u l A nd S ca l e < < < 3 2 , 256 > > > \

( d_ sig na l , d _ f i l t e r _k er ne l , ne w _s ize , 1. 0 f / ne w_ si ze

);

// Check if kernel execution generated and error

CU T _ C HE C K_ E R R OR \

(" Ke rn el f ai le d [ C o m p l e x Po i nt w is e Mu l An d S c a l e ] " );

// Transform signal back

cu f f t Ex e c C 2C ( plan , ( c u ff t C o mp l e x *) d_ s ig nal , \

( c uf f tC om p le x *) d _s i gn al , C UF F T _ IN V E R SE ) ;

[. . .]

}

been the re-computation of reference signal FFT. At

every cycle, in fact, a new chunk of ref. signal and

a new scrambling code would have been pushed to

the cudaCrossCorr function, that would have done the

FFT twice per iteration and then apply convolution

theorem, multiplying the resulting vectors and anti-

transform the result. Designed to work on multiple

cross correlations per session sharing the reference

signal, instead, using static variables to keep track of

how many FFT have been computed, on which part

of incoming signal and most important where results

are stored in memory, cudaCrossCorr can save up to

30% computing power (1 out of 3 FFT-based opera-

tions) per cycle, with a great advantage in terms of

execution time. See details in Listing 1 to see how

this simple mechanism works.

The only non-masked operation in cudaCrossCorr

body is the recombination of spectra after FFT execu-

tion, ( f

∗

∗ g) in eq. 1.

3.2 About Precision in

Cross-correlation

Several numeric tests have been executed, using

MATLAB as golden standard with its xcorr function

that implements circular cross correlation, computed

in double precision IEEE-754, complex arguments.

CUDA Version showed overall good perfor-

mances when compared to reference standard. See

Figure 4. CUDA FFT crossCorr, matched against

MATLAB FFT xcorr shows a residual term in the

order of ±5.0 · 10

−6

, so perfectly in line with expec-

tations for single precision 32 bit arithmetic of G92

cores.

ippsCrossCorr32fc on the other hand shows al-

most the same performance (single precision) on the

whole signal length, not visible for bigger Y scale,

with a notable exception on master signal’s tail. When

overlap between reference and template signal ex-

ceeded former’s length, cross correlation index starts

dropping towards zero, for effect of zero padding in-

side the matching function. Even if this behavior

has no practice relevance when looking for “best”

match (cross correlation index is guaranteed to be-

come lower than in other parts of data), it could have

dangerous effects if resulting vector will be normal-

ized against its L1 or L2 norm. These manipulations

are quite frequent in digital signal processing, and in

this case such these results could imply a loss of pre-

cision of successive steps of computation.

4 COMPUTATIONAL

CONSIDERATIONS

AND BENCHMARKS

As previously shown in CrossCorr code analysis, all

FFT computations have been ofﬂoaded from CPU

to GPU, and in ﬁrst instance this process was ﬂaw-

less and simple thanks to the CUFFT library usage.

CUFFT provides a simple interface for computing

parallel FFTs on an NVIDIA GPU, which allows

users to leverage the ﬂoating point power and paral-

lelism of the GPU without having to develop a cus-

tom, GPU based FFT implementation. FFT libraries

typically vary in terms of supported transform sizes

and data types. CUFFT API is modeled after FFTW

(see http://www.fftw.org), which is one of the most

popular and efﬁcient CPU based FFT libraries.

Sadly, CUFFT implementation, or at least un-

til v2.1 of CUDA Toolkit, even showing a general

speedup against the underlying CPU structure (> 40

GFlop/s for a grand total of > 20 GB/s on GeForce

G92 8800GTS 512), doesn’t exploited the full poten-

tial of NV’s hardware computing power. That library

is in fact a collection of 5 different implementations

of part of Cooley-Turkey structure, often referred as

Radix2 FFT Scheme as in (Tian et al., 2004), extend-

ing it to cardinality of 3,4 and 5 elements per block,

thus adding to their library the capability to use also

Radix-3, Radix-4 and Radix-5 schemes.

Well accepted theory of “Mixed radix FFT

schemes” is described in detail in (Stasinski and

the re-computation of reference signal FFT. At ev-

ery cycle, in fact, a new chunk of ref. signal and

a new scrambling code would have been pushed to

the cudaCrossCorr function, that would have done the

FFT twice per iteration and then apply convolution

theorem, multiplying the resulting vectors and anti-

transform the result. Designed to work on multiple

cross correlations per session sharing the reference

signal, instead, using static variables to keep track of

how many FFT have been computed, on which part

of incoming signal and most important where results

are stored in memory, cudaCrossCorr can save up to

30% computing power (1 out of 3 FFT-based opera-

tions) per cycle, with a great advantage in terms of

execution time. See details in Listing 1 to see how

this simple mechanism works.

The only non-masked operation in cudaCrossCorr

body is the recombination of spectra after FFT execu-

tion, ( f

∗

∗ g) in eq. 1.

3.2 About Precision in

Cross-correlation

Several numeric tests have been executed, using

MATLAB as golden standard with its xcorr function

that implements circular cross correlation, computed

in double precision IEEE-754, complex arguments.

CUDA Version showed overall good perfor-

mances when compared to reference standard. See

Figure 4. CUDA FFT crossCorr, matched against

MATLAB FFT xcorr shows a residual term in the

order of ±5.0 · 10

−6

, so perfectly in line with expec-

tations for single precision 32 bit arithmetic of G92

cores.

ippsCrossCorr32fc on the other hand shows al-

most the same performance (single precision) on the

whole signal length, not visible for bigger Y scale,

with a notable exception on master signal’s tail. When

overlap between reference and template signal ex-

ceeded former’s length, cross correlation index starts

dropping towards zero, for effect of zero padding in-

side the matching function. Even if this behavior

has no practice relevance when looking for “best”

match (cross correlation index is guaranteed to be-

come lower than in other parts of data), it could have

dangerous effects if resulting vector will be normal-

ized against its L1 or L2 norm. These manipulations

are quite frequent in digital signal processing, and in

this case such these results could imply a loss of pre-

cision of successive steps of computation.

4 COMPUTATIONAL

CONSIDERATIONS

AND BENCHMARKS

As previously shown in CrossCorr code analysis, all

FFT computations have been ofﬂoaded from CPU

to GPU, and in ﬁrst instance this process was ﬂaw-

less and simple thanks to the CUFFT library usage.

CUFFT provides a simple interface for computing

parallel FFTs on an NVIDIA GPU, which allows

users to leverage the ﬂoating point power and paral-

lelism of the GPU without having to develop a cus-

tom, GPU based FFT implementation. FFT libraries

typically vary in terms of supported transform sizes

and data types. CUFFT API is modeled after FFTW

(see http://www.fftw.org), which is one of the most

popular and efﬁcient CPU based FFT libraries.

Sadly, CUFFT implementation, or at least un-

til v2.1 of CUDA Toolkit, even showing a general

speedup against the underlying CPU structure (> 40

GFlop/s for a grand total of > 20 GB/s on GeForce

G92 8800GTS 512), doesn’t exploited the full poten-

tial of NV’s hardware computing power. That library

is in fact a collection of 5 different implementations

of part of Cooley-Turkey structure, often referred as

Radix2 FFT Scheme as in (Tian et al., 2004), extend-

ing it to cardinality of 3,4 and 5 elements per block,

thus adding to their library the capability to use also

Radix-3, Radix-4 and Radix-5 schemes.

Well accepted theory of “Mixed radix FFT

schemes” is described in detail in (Stasinski and

Potrymajo, 2004). Radix-3 and Radix-5 schemes use

FAST TEMPLATE MATCHING FOR UMTS CODE KEYS WITH GRAPHICS HARDWARE

269

(a) CUDA vs. MATLAB.

(b) CUDA vs. IPP.

Figure 4: xCorr precision comparisons.

respectively 35% and 17% more add-mul operations

than Radix-2, but for certain sequence lengths Radix-

2 have high probability to hit a cache miss when look-

ing up for input operands. Once again, source code

for CUFFT for scheduling part, the one spawning the

computing threads, is not available in source format,

and so we can’t ﬁgure how authors handled such these

optimization problems.

These speculations, anyway, can suggest us an in-

teresting direction to focus attention to develop better

code for GPU. Some points:

• FFT stages show a pre-computable locality of in-

put arguments. it is possible to know in advance

which data chunks are needed in a processor in a

warp, for each step.

• Increasing local FFT size (Radix-3,4,5...N-k) will

increase computing time for node, but also will

represent a leap forward in stage’s map.

• Increasing local FFT size will increase probability

of cache miss in input argument, but this event is

related to local cache size.

4.1 Increasing Radix Size Approach

The few considerations above are valid for any com-

puting environment, as they’re resulting from algo-

rithmic analysis, but have great effect when applied

to NVidia GPUs context. All the points highlight

the need for local cache of arguments (see (Frigo

et al., 1999)), as picking them up from central mem-

ory would represent a great penalty in terms of laten-

cies and so for global execution times. Using global

memory in GPU is even more problematic than in

CPU, due to lack of pre-fetching units for each pro-

cessor in the array (there is a central memory handler

that pushes data to the common bus). Memory laten-

cies for GPU can sum up to 400 cycles for a single

transfer, and for this reason keeping low the risk of

cache miss is mandatory. Register ﬁle for each pro-

cessor in the array counts up to 32 entries, with low-

est latency access, but it would not be large enough to

improve data chunk size for thread.

In our help comes the shared memory structure,

16KBytes in pre-GT200 series of CUDA-enabled

GPUs, that has low time access too and can be used

just declaring variables with shared attribute.

NVCC will understand the memory map to be put

in shared separated space, and will push data closer

to processing units. This memory bank is shared on

Multiprocessor basis, and so many threads can access

in parallel to these information.

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

270

4.2 Numerical Benchmarks

In (Volkov and Kazian, 2008) is shown an imple-

mentation of the FFT that achieves 160 GFlop/s on

the GeForce 8800 GTX, which is 3x faster than 50

GFlop/s offered by the CUFFT. It is designed for N =

512, which is hard-coded. Later in the text this ver-

sion will be referred as ”VV” code. The implemen-

tation also includes cases n = 8 and n = 64 working

in a special data layout. This implementation lacked

of support for inverse FFT, and moreover used a not

CUFFT-like calling scheme. It was so updated and

tested always against MATLAB to test precision and

CUFFT to benchmark performances. Special kernels

for Complex Conjugate operations have been sup-

plied externally, as reported in Listing 1. This latter

version, which is the most performant one, will be re-

ferred as ”VV+MV mod” later in the tables.

Using shared memory banks, and keeping N sizes

as power of two even in internal stages produces a

huge speedup, especially on longer sequences where

CUFFT likely spawns a very high number of comput-

ing threads. Using mixed radix sizes, moreover, it is

very hard to keep summation error as low as possi-

ble, as input terms for recombination are divided by

odd numbers, and more in general not for 2. For

this reason, on longer sequences, CUFFT shows a

not optimal precision measure and always higher than

VV+MV implementation. All the tests were executed

for FFT/iFFT sequences.

Some FFT benchmarks between standard CUFFT

design and VV+MV one. CUDA Toolkit v.2.1 on XP

32 bit used. Errors reported are in order of 1 ULP for

IEEE-754 32 bit data.

Device: GeForce 8600M GS

900 MHz clock, 256 MB memory

(CUDA Toolkit v. 2.1 - Windows XP 32 bit)

CUFFT VV+MV mod

N / Batch GFlop/s GB/s Err GF/s GB/s Error

8 / 524288 0.4 0.4 1.8 7.2 7.7 1.6

64 / 65536 2.5 1.4 2.3 10.5 5.6 2.2

512 / 8192 2.9 1.0 2.9 12.3 4.4 2.5

Device: GeForce 8800 GTS 512

1674 MHz clock, 512 MB memory

(CUDA Toolkit v. 2.1 - Windows XP 32 bit)

CUFFT VV+MV mod

N / Batch GFlop/s GB/s Err GF/s GB/s Error

8 / 524288 6.0 6.3 1.8 46.5 49.6 1.6

64 / 65536 37.6 20.1 2.3 94.4 50.3 2.2

512 / 8192 43.4 15.4 2.9 125.4 44.6 2.5

10 km!

Figure 5: WIND3G Sensitivity improvements in a

GPS-tagged context.

In late 2009, NVidia released in 2.3 beta version

of their CUDA toolkit an updated CUFFT library,

with matches best performances above on longest se-

quences. Anyway, it still doesn’t handle properly

shorter length vectors (used often in multimedia pro-

cessing, expecially for noise samples in audio digital

restores).

Here are the same tests with updated values.

Device: GeForce 8800 GTS 512

1674 MHz clock, 512 MB memory

(CUDA Toolkit v. 2.3beta - Windows XP 32 bit)

CUFFT VV+MV mod

N / Batch GFlop/s GB/s Err GF/s GB/s Error

8 / 524288 5.7 6.1 1.7 45.9 49.0 1.6

64 / 65536 36.2 19.3 2.4 92.8 49.5 2.2

512 / 8192 129.1 45.9 2.1 121.9 43.4 2.5

5 CONCLUSIONS

UMTS code scrambling service has proven to be a

very demanding task in a production environment.

FAST TEMPLATE MATCHING FOR UMTS CODE KEYS WITH GRAPHICS HARDWARE

271

Before the CUDA solution was developed, the mobile

system to be used on the ﬁeld should have been pow-

ered by a HPC-like system, with an obvious expen-

sive price tag - and really power hungry (> 2 × 400

Watts). On the road, such a requirement is to be

considered stressful for ﬁnal users. The CUDA im-

provement enabled Wider Networks to ship a really

mobile system, based upon a standard off-the-shelf

GPU equipped laptop, to be used in companion to the

WIND3G Scanner. Total cost of ownership of such

a system is considerably lowered w.r.t to the original

setup. On the results side, the most notable improve-

ment is the higher sensitivity of the scanning proce-

dure, as shown in Figure 5 with a substantially lower

energy used in a shorter computation time slice. As

side effect, CPU+GPU usage, better scheduled in self-

containing computing threads, lowered the total load

to the underlying OS from ≥ 90% to < 35%.

REFERENCES

Bornkessel, C. and Wuschek, M. (2006). Exposure mea-

surements of modern digital broadband radio services.

Technical report, IMST GmbH, Test Centre EMC,

Kamp-Lintfort, Germany University of Applied Sci-

ences Deggendorf, Edlmairst, Deggendorf, Germany.

Frigo, M., Leiserson, C. E., Prokop, H., and Ramachan-

dran, S. (1999). Cache-oblivious algorithms. In

In Proc. 40th Annual Symposium on Foundations of

Computer Science, pages 285–397. IEEE Computer

Society Press.

Stasinski, R. and Potrymajo, J. (2004). Mixed-radix fft for

improving cache performance. EUSIPCO 2004, Pro-

ceedings of.

Tian, J., Xu, Y., Jiang, H., Luo, H., and Song, W. (2004).

Efﬁcient algorithms of fft butterﬂy for ofdm systems.

In Emerging Technologies: Frontiers of Mobile and

Wireless Communication, 2004. Proceedings of the

IEEE 6th Circuits and Systems Symposium on, vol-

ume 2, pages 461–464 Vol.2.

Volkov, V. and Kazian, B. (2008). Fitting fft onto g80 ar-

chitecture. Technical Report CS 252, University of

California, Berkeley.

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

272