PETRI NET BASED APPROACH TO TEST BENCH
CONSTRUCTING FOR DATAPATH
Andrei Karatkevich
Institute of Computer Science and Electronics, University of Zielona Gora, Podgorna 50, Zielona Gora, Poland
Keywords:
System design, Data path, Test bench, Simulation, Verification, Petri nets.
Abstract:
Testing a data path in a digital system such as a microcontroller requires checking every possible way of
sending data between the functional units. This paper considers a task of generating a test bench for a given
data path, which covers every way of data sending with minimized number of simulations of microinstructions.
We present a method in which a data path is modeled by a Petri net. The task of optimal test bench generation is
formulated as a task of covering all transitions by a sequence with minimal length. It can be solved by finding
certain T-invariant of the net and a firing sequence corresponding to it. The proposed method is illustrated by
two case studies of testing data paths of simple processors.
1 INTRODUCTION
The von Neumann computer architecture defines the
control unit as a distinct part of a design. Nowadays,
a digital system is often considered as a composition
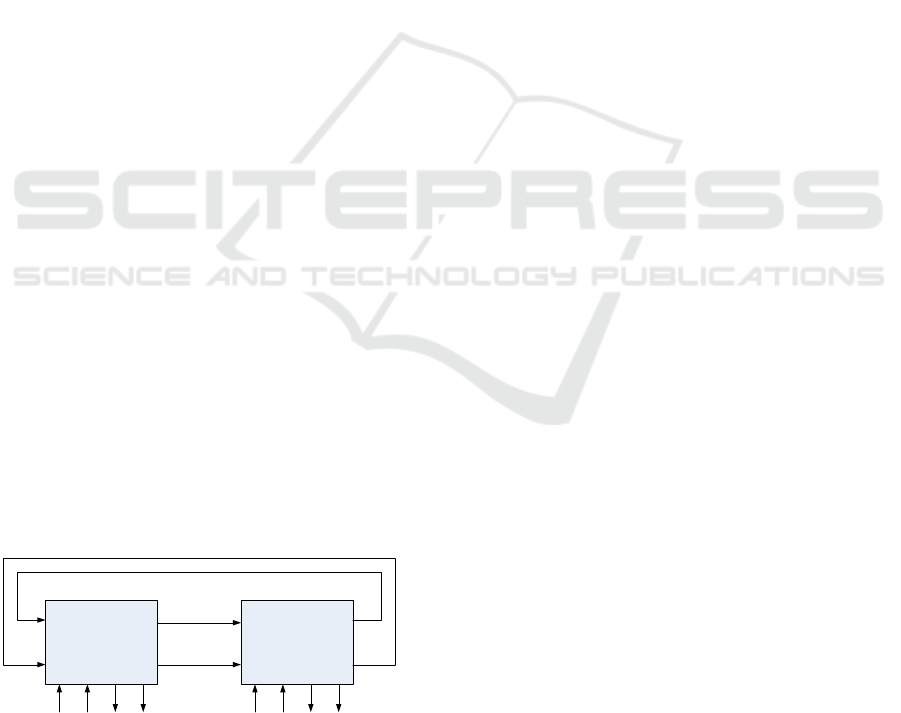
of control unit (CU) and data path (DP) (Fig. 1). The
separate synthesis methods for data path and control
unit are developed (Baranov, 2008; Barkalowand We-
grzyn, 2006; Wisniewski, 2009).
Figure 1: Digital system as a composition of CU and DP.
To verify a formal specification of a design, a test
bench should be constructed. Among the necessary
components of a test bench there are input vectors
(stimuli) and the expected output vectors. The de-
sign is simulated with the stimuli at its input, and the
output values being the result of simulation are com-
pared to the expected values. If there is a difference
between them, then the mistakes in the design are de-
tected (Baranov, 2008).
As far as data path and control unit are designed
separately, it is reasonable to test them also separately,
constructing special test bench for each of them. Data
path consists of such units as memory blocks, regis-
ters, arithmetic logic units, counters, multiplexors and
so on. For testing a data path it is necessary to check
every direct connection between its units at least once.
But it is possible to write some input data directly
only to the inputs of a DP. We also suppose that it is
possible to read data only from the ”output” units. If
a data path is represented by an oriented graph, where
nodes correspond to the data path units, and arcs cor-
respond to direct data sending between the units (a
connection graph), then the task of data path testing
can be presented as a task of covering all arcs of the
graph by the paths from its start nodes to end nodes.
Note that ”sending” data from a data path unit to it-
self (such as operation i := i + 1, where i is imple-
mented as a counter) also should be checked; such
situation can be represented in a connection graph as
a self-loop. Also, every microinstruction should be
checked, even if two or more microinstructions send
data between the same pair of units (it means that a
connection graph may have multi-edges).
An algorithm for automated generation of a test-
ing sequence of microinstructions for data path by
means of connection graph covering is presented in
(Karatkevich and Baranov, 2010); the task is reduced
to one of the variants of the route inspection problem,
which can be effectively solved. But there is a prob-
lem with the graph-based approach: if a microinstruc-
506
Karatkevich A..
PETRI NET BASED APPROACH TO TEST BENCH CONSTRUCTING FOR DATAPATH.
DOI: 10.5220/0003363105060511
In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2011), pages
506-511
ISBN: 978-989-8425-48-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

tion may contain several microoperations (which is
usual for control units (Baranov, 2008)), then one mi-
croinstruction may send data between more than two
data path units. A test sequence consists of microin-
structions, not of microoperations. Then we cannot
directly obtain a test sequence from a path in a data
path connection graph. So it is reasonable to model
a data path not just by a graph, but by a Petri net
(where a transition represents a microinstruction), and
to solve the task by generating a minimized firing se-
quence covering all its transitions. The presented pa-
per describes an algorithm of test sequence generation
for data path, using Petri net as a data path model.
2 PETRI NETS
Petri nets are used as one of the basic models of
concurrent discrete systems (Murata, 1989; Peterson,
1981). A Petri net can be considered as a bipartite ori-
ented graph with two kinds of nodes: places and tran-
sitions (Fig. 2). Places of a net may contain tokens,
and a configuration of the tokens is called a mark-
ing (state) of the net. A marking is denoted as M,
with some indexes if needed. A marking is safe if
no place contains more than one token. A marking
can be changed by firing (execution) of the enabled
transitions. An enabled transition is such transition
that every its input place (a place from which an arc
leads to the transition) contains a token. Transition fir-
ing removes a token from each input place and adds
a token to each output place (a place to which an arc
leads from the transition) of it. Note that we will need,
among others, the transitions without input or output
places. A transition without input places is always en-
abled; a transition without output places, when firing,
does not add any token anywhere.
For a Petri net N with n transitions and m places,
the incidence matrix A = [a
ij
] is an m× n matrix such
that
a
ij
= a
+
ij
− a
−
ij
(1)
where a
+
ij
= 1 if and only if place p
j
is an output place
of transition t
i
, otherwise a
+
ij
= 0; and a
−
ij
= 1 if and
only if place p
j
is an input place of transition t
i
, oth-
erwise a
−
ij
= 0. Every a
ij
represents the number of
tokens changed in place p
j
by firing of transition t
i
.
An integer n-vector x is a T-invariant, if A
T
x = 0.
A firing count vector of a firing sequence (a se-
quence of transition firings) σ is an n-vector of non-
negative integers σ such that the ith entry of σ denotes
the number of times transition t
i
fires in sequence σ.
Theorem 1 (Murata, 1989): An n-vector x ≥ 0 is a
T-invariant if and only if there exists a marking M and
firing sequence σ from M back to M with its firing
count vector σ = x.
σ
Figure 2: An example of Petri net.
3 IDEA OF THE METHOD
Let us construct for given data path a modeling Petri
net in the following way. A place corresponds to ev-
ery data path unit; a transition t
i
corresponds to every
microinstruction Y
i
, and a place p
j
is an input place
for t
i
if and only if there is a microoperation in Y
i
such
that it sends data from the unit corresponding to p
j
;
place p
k
is an output place for t
i
if and only if there
is a microoperation in Y
i
such that it sends data to the
unit corresponding to p
k
.
Now, let us remove every place corresponding to
an input or output data path unit. It will cause that
our net will have transitions without input places and
transitions without output places. Indeed, at any mo-
ment we can write data to the input units and read
from the output units. Hence any firing sequence in
the obtained net will correspond to a possible way of
data sending in the data path.
Suppose that initially the Petri net has no tokens.
The tokens can be introduced by firing the transitions
without input places. Any nonempty firing sequence
leading from empty marking back to empty marking
corresponds to data sending from input to output units
of the data path. As follows from Theorem 1, a T-
invariant corresponds to every such firing sequence.
By finding a T-invariant x > 0 we can find a firing se-
quence coveringall transitions, which will correspond
to a sequence of microinstructions allowing to check
every connection in the data path.
To find the T-invariants, it is necessary to solve
the system of linear equations A
T
x = 0. It can be
solved by Gauss’ method (Hefferon, 2008). Then,
finding among the set of solutions one which consists
of positive integers and has minimal sum of values of
PETRI NET BASED APPROACH TO TEST BENCH CONSTRUCTING FOR DATAPATH
507

the variables is a linear programming task which can
be solved by the simplex method or another appro-
priate method (Vanderbei, 2008). When the minimal
T-invariant covering all transitions is obtained, a cor-
responding firing sequence can be calculated from it.
The test sequence of the microinstructions can be ob-
tained from the firing sequence.
4 THE PROPOSED ALGORITHM
Below the algorithm of test sequence generation is
presented.
1. Create a Petri net N, where places correspond to
the internal data path units, and transitions corre-
spond to possible data transfers between the units
(including input and output ones); one transition
corresponds to one microinstruction.
2. Solve the system of linear equations A
T
x = 0 by
Gauss’ method. Note that the rows of A corre-
sponding to the self-loops and to direct data send-
ing from input to output units consist of zeros. As
far as any values of the corresponding entries of
a T-invariant are possible, use value 1 of them. If
the system has no solutions, go to step 7.
3. Find the solution consisting of positive integers
with minimal sum. It can be formulated as a lin-
ear programming problem with the function to be
maximized f(x) = − x
1
− x
2
− ... − x
n
(note that
not every x
i
is a free variable) and problem con-
strains x
1
> 0, x
2
> 0, ..., x
n
> 0. If the problem
has no trivial solution, it can be solved by the sim-
plex method.
4. Construct for the selected solution (T-invariant)
x a firing sequence σ with its firing count vec-
tor equal to x such that every reached marking is
safe. To do that, simulate firing of the transitions
according to their number in x, starting from the
empty marking. If an unsafe marking is obtained
or a marking in which not all transitions have fired
appropriate number of times but none of them is
enabled, then the constructing should backtrack,
returning to the most resent transition where an-
other possibility of firing existed, and try another
possibility. If the algorithm fails to construct σ for
x, go to step 8.
5. Construct for the firing sequence σ corresponding
sequence of microinstructions for the test bench
in the following way. Scan the firing sequence.
For every transition t
i
add the corresponding mi-
croinstruction Yi, if and only if in the sequence of
microinstructions there is no previous entry of Yi
such that no microinstruction between those en-
tries writes data to at least one of data path units
to which Yi writes or from which it reads.
6. The test sequence is constructed successfully. The
end.
7. Constructing of the test sequence failed (this pos-
sibility is discussed below). The end.
8. Constructing of the test sequence failed, an incon-
sistency in the design is detected (this possibility
is discussed below). The end.
5 EXAMPLES
5.1 General Information
For the examples we use the designs created by means
of the experimental EDA tool Abelite which imple-
ments high-level synthesis and a very fast optimizing
synthesis of FSM and combinational circuits (Bara-
nov, 2008; Baranov, 2009). The Abelite design
methodology follows the common model in which
any digital system is regarded as a composition of
control unit and data path. One of the main concepts
used in this methodology is the construction of the
so-called naked data path, which doesn’t contain any
cloud circuits, only standard regular units. The data
path design is described in detail in (Baranov, 2008).
5.2 A Simple Processor
As the first example we use a design of a very simple
processor implementing two operations - the bubble
sort and the search of the maximal element. It is an
improved version of the design described in (Bara-
nov, 2009). List of its microinstructions is presented
in Table 1. The connection graph of the data path is
presented in Figure 3.
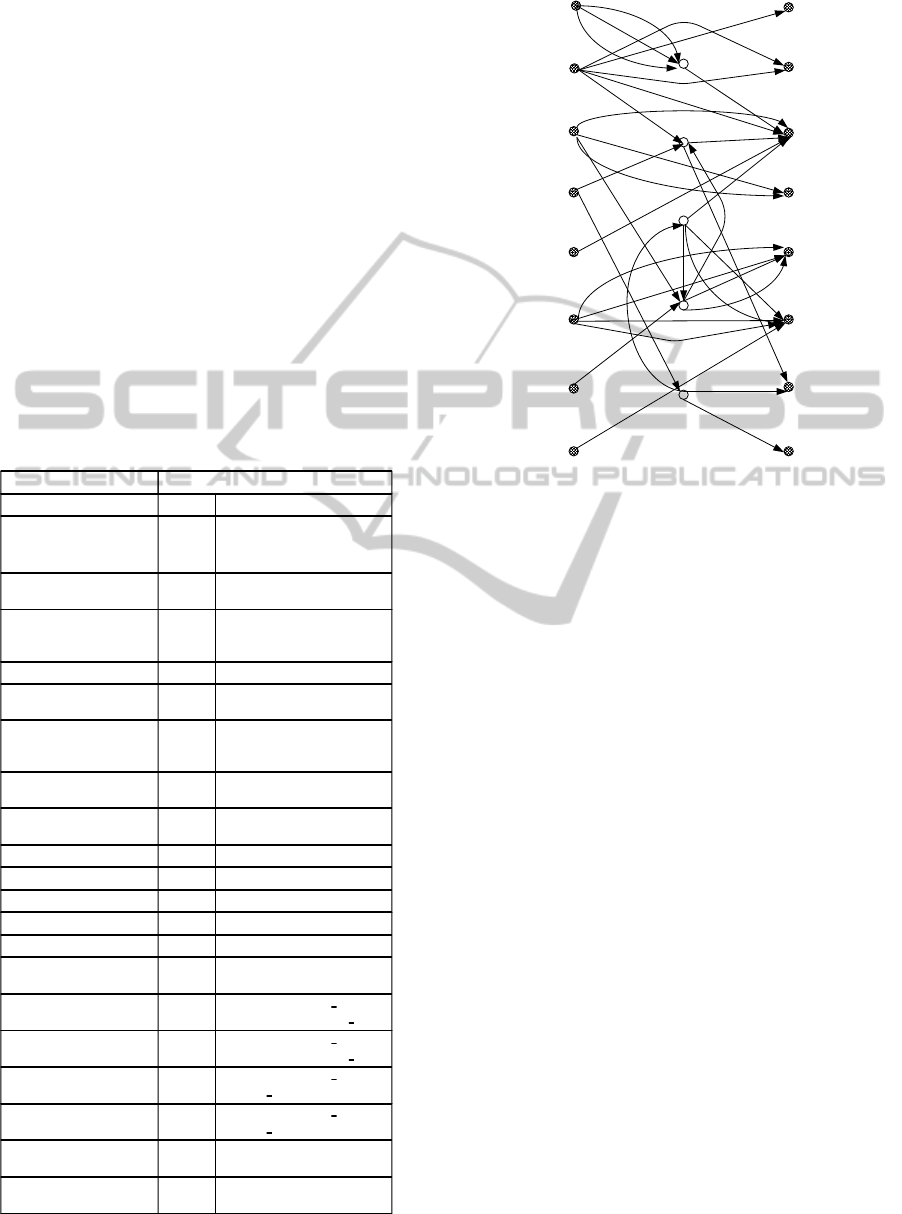
The Petri net modeling the data path is shown in
Figure 4. ”Non-existing” places (corresponding to in-
put and output data path units) and the incident arcs
are dashed. Numbers of transitions correspond to
numbers of microinstructions.
The T-invariants for the net shown in Figure 4 can
be obtained by solving the following system, where
numbers of variables correspond to numbers of tran-
sitions in Figure 4:
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
508

Figure 3: Connection graph for the first example.
Figure 4: Petri net modeling the data path.
−x
18
+ x
19
= 0
x
6
− x
7
− x
8
+ x
10
+ x
16
= 0
x
1
+ x
5
− x
9
− x
21
= 0
x
11
− x
15
− x
18
= 0
x
1
− x
8
+ x
9
− x
10
+ x
15
− x
16
= 0
−x
3
+ x
8
− x
13
− x
16
− x
17
− x
20
= 0
x
3
− x
10
+ x
13
− x
17
− x
20
= 0
(2)
Table 1: Functional microinstructions and microoperations
for the first example.
Y1
y16
y25
i:=0
mac:=0
Y2 y28 mac:=mac+1
Y3 y31 r2:=r1
Y4 y17 i:=i+1
Y5 y16 i:=0
Y6
y20
y23
m[m adr]:=ext out
m
adr:=ext adr
Y7
y15
y23
ext in:=m[m adr]
m
adr:=ext adr
Y8
y24
y30
m adr:=mac
r1:=m[m
adr]
Y9 y26 mac=i
Y10
y20
y23
m[m adr]:=r2
m
adr:=mac
Y11 y18 j:=0
Y12 y19 j:=j+1
Y13
y28
y31
mac:=mac+1
r2:=r1
Y14 y29 mac:=mac-1
Y15 y27 mac:=j
Y16
y20
y23
m[m adr]:=r1
m
adr:=mac
Y17
y8
y12
comp16 in1:=r1
comp16
in2:=r2
Y18
y7
y13
comp16 in1:=j
comp16
in2
:=tempReg16
Y19
y2
y32
alu16 in1:=n
tempReg16:=alu16
Y20
y9
y11
comp16 in1:=r2
comp16
in2:=r1
Y21
y6
y10
comp16 in1:=i
comp16
in2:=n
The solution set can be described by the following
equations:
x
1
= −x
9
+ 2x
10
− x
15
+ 2x
16
+ 2x
17
+2x
20
x
3
= x
10
− x
13
+ x
17
+ x
20
x
5
= 2x
9
− 2x
10
+ x
15
− 2x
16
− 2x
17
−2x
20
+ x
21
x
6
= x
7
+ 2x
17
+ 2x
20
x
8
= x
10
+ x
16
+ 2x
17
+ 2x
20
x
11
= x
15
+ x
19
x
18
= x
19
(3)
The function which should be minimized (keep-
ing all free and bound variables positive integers)
is
∑
21
i=1
x
i
= x
2
+ x
4
+ 2x
7
+ 2x
9
+ 3x
10
+ x
12
+ x
14
+
2x
15
+ 2x
16
+ 6x
17
+ 3x
19
+ 6x
20
+ 2x
21
. One of the
minimal solutions (the T-invariant we are looking for)
is (3, 1, 2, 1, 2, 5, 1, 6, 4, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1).
The following firing sequence can be obtained
from this T-invariant:
PETRI NET BASED APPROACH TO TEST BENCH CONSTRUCTING FOR DATAPATH
509
t
1
t
2
t
4
t
6
t
7
t
6
t
8
t
3
t
6
t
9
t
5
t
8
t
6
t
9
t
5
t
11
t
12
t
14
t
17
t
8
t
3
t
6
t
15
t
8
t
9
t
10
t
1
t
11
t
13
t
8
t
9
t
16
t
1
t
8
t
19
t
18
t
20
t
21
.
The resulting test sequence is:
Y
1
Y
2
Y
4
Y
6
Y
7
Y
8
Y
3
Y
9
Y
5
Y
8
Y
11
Y
12
Y
14
Y
17
Y
8
Y
15
Y
10
Y
13
Y
16
Y
8
Y
19
Y
18
Y
20
Y
21
.
5.3 A More Complex Processor
As the second example we use more complex and re-
alistic design - a 16-bit processor described in (Bara-
nov, 2008). To save place we limit our consideration
only to the 16-bit microoperations which transfer in-
formation from the output of one unit to the input of
another unit (excluding the operations which are exe-
cuted in one operational unit). List of such microop-
erations and corresponding microinstructions is pre-
sented in Table 2. The connection graph of the data
path is presented in Figure 5.
Table 2: Microinstructions and 16-bit microoperations for
the second example
Y1 y2 BoR[AdrW]:=RALU
Y2
y5
y6
y8
ALU1:=BoR[AdrR1]
ALU2:=BoR[AdrR2]
RALU:=ALU
Y3
y6
y8
ALU2:=BoR[AdrR2]
RALU:=ALU
Y4
y12
y13
Adr1:=IR2
BoR[AdrW]
:=M1[Adr1]
Y5 y14 BoR[AdrW]:=IR2
Y6 y15
BoR[AdrW]
:=BoR[AdR2]
Y7
y12
y16
Adr1:=IR2
M1[Adr1]
:=BoR[AdrR1]
Y8 y18
BoR[AdrW]
:=BoR[AdrR1]
Y9
y5
y8
ALU1:=BoR[AdrR1]
RALU:=ALU
Y10 y19 PC:=BoR[AdrR2]
Y11 y20 PC:=IR2
Y13 y22 BoR[AdrW]:=InpR
Y14 y24 OutR:=BoR[AdrR1]
Y17 y28 PC:=x"FFFE"
Y18
y30
y31
Adr1:=x"FFFF"
M1[Adr1]:=PC
Y19
y32
y33
Adr0:=Ext Adr
M0[Adr0]:=Ext
Out
Y20
y34
y35
Adr1:=Ext Adr
M1[Adr1]:=Ext
Out
Y21
y34
y36
Adr1:=Ext Adr
Ext
in:=M1[Adr1]
Y22
y32
y37
Adr0:=Ext Adr
Ext
in:=M0[Adr0]
Y24
y39
y40
Adr0:=PC
IR1:=M0[Adr0]
Y25
y39
y41
Adr0:=PC
IR2:=M0[Adr0]
!
"#
$
$
"
%&
"
Figure 5: Connection graph for the second example.
The modeling Petri net is not shown, because in
this case it is too complex to be readable. There are
5 internal blocks in this datapath: RALU, M0[Adr0],
M1[Adr1], IR2 and PC. So the system of equations
which should be solved to obtain the T-invariants con-
sists of 5 equations (numbers of the variables corre-
spond to the numbers of microinstructions):
−x
1
+ x
2
+ x
3
+ x
9
= 0
x
19
− x
22
− x
24
− x
25
= 0
−x
4
+ x
7
+ x
18
+ x
20
− x
21
= 0
−x
4
− x
5
− x
7
− x
11
+ x
25
= 0
x
10
+ x
11
+ x
17
− x
18
− x
24
− x
25
= 0
(4)
Its minimal positive integer solution is:
(x
1
, x
2
, x
3
, x
4
, x
5
, x
7
, x
9
, x
10
, x
11
, x
17
, x
18
, x
19
, x
20
, x
21
,
x
22
, x
24
, x
25
) = (3, 1, 1, 1, 1, 1, 1, 4, 1, 1, 1, 6, 1, 2, 1, 4).
After constructing a firing sequence cor-
responding to this T-invariant (item 4 of the
algorithm) and test sequence corresponding
to the firing sequence (item 5) we obtain:
Y
2
Y
1
Y
3
Y
1
Y
9
Y
1
Y
10
Y
18
Y
19
Y
21
Y
20
Y
21
Y
22
Y
24
Y
25
Y
5
Y
7
Y
17
Y
25
Y
11
Y
25
Y
4
Y
6
Y
8
Y
13
Y
14
. This sequence covers every
connection and is more representative than the
”hand-made” sequence presented in (Baranov, 2008).
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
510

6 WHEN THE METHOD FAILS
As it can be seen from the description of the algo-
rithm, the situations are possible in which it fails to
generate a test sequence. It happens when there is no
T-invariant x > 0 for the modeling Petri net or when
for the obtained T-invariant the appropriate firing se-
quence does not exist. The second variant means two
possibilities: there is no firing sequence for the ob-
tained T-invariant that starts in empty marking or such
sequence exists, but leads through an unsafe marking.
Three mentioned situations are illustrated in Figure 6.
Figure 6: Examples of nets for which the method fails to
generate the sequence.
The first of them (Figure 6a; there is no T-invariant
without zero entries) corresponds to a case which is
not impossible (however rather untypical) in a correct
design. In this case any sequence of microinstructions
which transfers data from input to output units of the
data path either reads more than once from the same
unit without writing to it between those readings (p
1
),
or writes to an internal unit without reading from it
(p
2
). Then the method described in (Karatkevich and
Baranov, 2010) can be applied.
Two other situations signalize that something is
wrong in the data path structure or in the structure of
microinstructions. If a firing sequence leading from
an empty marking back to itself and covering all tran-
sitions does not exist (Figure 6b), then there is an in-
ternal unit (p
3
) from which data are read before writ-
ing in it. If such firing sequence exists but has to go
through an unsafe marking (Figure 6c), then there is
a unit (p
2
) to which data are written more than once
without reading from it between those writings, which
means that some data are lost.
7 CONCLUSIONS
The proposed method provides possibility of auto-
mated generation of sequences of microinstructions
for testing data path of a digital design constructed
as a composition of a data path and a control unit.
Such sequence is a necessary part of a test bench. The
method we proposetakes into account structure of mi-
croinstructions, which may consist of several micro-
operations. Using Petri net as a model of data path
was found to be suitable for such cases.
However, the method described here at first gener-
ates a long sequence with multiple repetitions of some
transitions and then constructs a sequence of microin-
structions which may be remarkable shorter. Further
research should concentrate on checking whether it
is possible to build a minimized sequence directly,
avoiding constructing a firing sequence correspond-
ing to the T-invariant of the modeling Petri net (as in
this method) or a postman tour in the modeling graph
(as in (Karatkevich and Baranov, 2010)).
ACKNOWLEDGEMENTS
I would like to thank Samary Baranov for inspiration,
fruitful discussions and consultations. The projects of
the processors used for the examples are developed by
him.
REFERENCES
Baranov, S. (2008). Logic and System Design of Digital
Systems. TGU, Tallinn.
Baranov, S. (2009). Asms in high level synthesis of eda
tool abelite. In Preprints of the 4th IFAC Workshop on
Discrete-Event System Design, IFAC, Gandia Beach,
pages 195–200. IFAC. (to appear online in IFAC-
PapersOnLine.net).
Barkalow, A. and Wegrzyn, M. (2006). Design of Con-
trol Units with Programmable Logic. University of
Zielona Gora, Zielona Gora.
Hefferon, J. (2008). Linear Algebra. electronic edition,
Colchester.
Karatkevich, A. and Baranov, S. (2010). Graph based ap-
proach to test bench constructing for datapath. In
IWK’10, 55th Internationales Wissenschaftliches Kol-
loquium, pages 662–667. Technische Universitaet Il-
menau.
Murata, T. (1989). Petri nets: properties, analysis and ap-
plications. Proceedings of the IEEE, 77:541–580.
Peterson, J. L. (1981). Petri net theory and the modeling of
systems. Prentice-Hall.
Vanderbei, R. J. (2008). Linear Programming: Foundations
and Extensions. Springer Verlag, 3rd edition.
Wisniewski, R. (2009). Synthesis of compositional micro-
program control units for programmable devices. Uni-
versity of Zielona Gora, Zielona Gora.
PETRI NET BASED APPROACH TO TEST BENCH CONSTRUCTING FOR DATAPATH
511
