TRAVERSING A BVH CUT TO EXPLOIT RAY COHERENCE
R. Torres, P. J. Mart
´
ın and A. Gavilanes
Departamento de Sistemas Inform
´
aticos y Computaci
´
on, Universidad Complutense de Madrid, Madrid, Spain
Keywords:
Coherence, Bounding volume hierarchy, CUDA, Path tracing, Ray tracing.
Abstract:
In this paper we study how to deal with the ray incoherence that naturally arises in path tracing-based systems.
We introduce the notion of BVH Cut to split the tree into a forest of disjoint subtrees. We will use it to
filter the rays that are successively generated by the path tracing algorithm. Each subtree is then traversed
by its corresponding group of rays. Despite the overload of filtering all the rays each time, a significant
profit is achieved. Nevertheless, constructing a BVH cut is a challenging task, because it can lead to a huge
amount of work if the same rays belongs to many groups. Thus, we present two kind of building heuristics:
structural heuristics that characterizes the root of a subtree by a property (the node’s depth or the surface area
of its bounding volume in this paper), and optimization heuristics that are based on the Simulated Annealing
method. The performance of traversing the cuts so built has been experimentally analyzed over four usual
scenes, using two popular implementations of the subtree traversal (persistent while-while / persistent packet).
The results show a relevant saving time w.r.t. the classic BVH traversal, that grows as the ray incoherence
increases. The best saving ranges from 32.0% / 40.9% for structural heuristics, to 32.0% / 51.7% for cuts built
with Simulated Annealing.
1 INTRODUCTION
One of the main bottlenecks for most ray tracing algo-
rithms is the traversal stage. Although great progress
has been made in their performance through the usage
of modern GPU architectures (Aila and Laine, 2009),
the success of efficiently traversing a great amount
of incoherent rays in parallel remains a challenging
topic, since it is highly connected to the programming
SIMD model of the hardware, and, more precisely,
to the way rays are arranged on the device. There-
fore, the notion of coherence is essential to under-
stand the behavior of SIMD-based implementations,
and more research on coherence is required to design
faster traversal procedures.
Although many definitions of coherence can be
found in the literature, most of them refer to a quali-
tative measure. Thereby, two rays are said to be co-
herent if they traverse the same nodes and triangles
most of the time. In order to exploit coherence in a
GPU, rays are usually grouped into packets, mainly to
allow the rays inside a packet to cooperate when read-
ing scene information from global memory. Thus, ray
packets become the traversal logical unit, which gives
rise to the so called packet-based traversals. Their
main disadvantage is that the rays inside a packet are
forced to traverse the hierarchy in the order the packet
chooses, which usually increases the total number of
nodes traversed w.r.t. the single-ray traversal. Hence,
the success of any packet-based traversal leans on
the assumption that the saving due to the cooperative
reading is greater than this traversal penalty. Conse-
quently, its success depends on the coherence inside
each packet, since the more coherent the rays of a
packet are, the higher the saving is.
Recently, (Aila and Laine, 2009) suggest that the
assumption is not valid for primary, one-bound dif-
fuse and ambient occlusion rays on modern GPUs.
Specifically, their experiments show that a stack-
based single-ray traversal is faster than a stack-based
packet traversal. Nevertheless, although the rays are
not grouped in explicit packets, they are implicitly
grouped since the SIMD model of GPUs is based on
the notion of warp. Therefore, the single-ray traver-
sal they compute can be actually considered packet-
based, since rays are arranged in the warps according
to a specific order (Z-order) of the image.
An important inconvenient of most coherence def-
initions is that it cannot be known before traversing
the tree. Thus, heuristics have to be used for packing
rays in order to obtain a high coherent level afterward.
In the literature, we can find two heuristics. On the
140
Torres R., J. Martín P. and Gavilanes A..
TRAVERSING A BVH CUT TO EXPLOIT RAY COHERENCE.
DOI: 10.5220/0003363401400150
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 140-150
ISBN: 978-989-8425-45-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b) (c) (d)
Figure 1: Scenes used for our testings. The images have been generated at a resolution of 1024 × 1024 with 1000 paths
per pixel (including primary rays). Each path is formed by 10 rays (each primary ray bounces 9 times). The total render-
ing times in SINGLE (persistent while-while) with Cut
root
are CONFERENCEROOM=552.7s (a), FAIRYFOREST=556.3s (b),
SPONZA=787.1s (c) and SIBENIK=815.4s (d). The total rendering time with the best structural depth Cuts in Table 1 and
inter-BVH pruning are CONFERENCEROOM=535.9s (3.03%), FAIRYFOREST=511.4s (8.07%), SPONZA=645.3s (18.01%)
and SIBENIK=605.9s (25.69%). The percentage in brackets are the saving w.r.t. Cut
root
.
one hand, coherence usually has a geometric mean-
ing: two rays are said to be geometrically coherent
whenever their origins lay “near” and/or the angle be-
tween their directions is “small” enough. Therefore,
the geometric coherent attempts to ensure a deeper
coherence, because it is expected for two geometri-
cally coherent rays to traverse the same nodes of the
acceleration structure.
So, it is also natural to suggest a behavioral mean-
ing: two rays are behaviorally coherent w.r.t. a node n
of the acceleration structure whenever both rays inter-
sect the bounding volume enclosing n. The underly-
ing idea behind behavioral coherence is that the accel-
eration structure drives the traversal for all the rays,
or an enough big set of the rays, simultaneously. In
fact, when a node is explored, only those rays inter-
secting its bounding volume are considered and the
rest of them have to be filtered. In that sense, parallel
GPU primitives, such as sorting, compact and (seg-
mented) scan functions, become essential for imple-
menting many tasks during the ray classification. No-
tice that the success of traversal then depends on the
performance of these primitives, and that, although
most of them are well known, their effective imple-
mentations on GPUs are relatively recent.
In this paper we research how to exploit the be-
havioral coherence when a great amount of incoher-
ent rays are shot through the scene, which is usual for
path tracing-based systems. Our main contribution is
double. On the one hand, we propose a BVH traver-
sal that begins classifying the rays on GPU accord-
ing to a sequence of descendants of the root, which
will be called Cut along the paper. This can be con-
sidered a breadth-first traversal for exploiting behav-
ioral coherence, since it results in a set of traversal
tasks involving behaviorally-coherent packets. Then,
these tasks are finally traversed in a classic depth-first
way on GPU. It is worth to mention that our approach
does not depend on the implementation of the traver-
sal that it is integrated into the system, since they are
fully interchangeable. We have actually tested two
of the fastest implementations on GPU –the persis-
tent packet and the persistent while-while by (Aila and
Laine, 2009)– yielding successful saving rates in both
cases.
On the other hand, we present different criteria
for building cuts that are compared each other regard-
ing the performance of their traversal over four usual
scenes. The results show a relevant saving time w.r.t.
the classic BVH traversal, that grows as the ray inco-
herence increases.
2 RELATED WORK
Ray Packets. (Wald et al., 2001) are pioneers in us-
ing ray packets for developing an interactive ray tracer
on CPU. They use the trivial geometric coherence of
neighboring pixels to pack primary rays. Packets al-
low to decrease memory traffic and improve the cache
efficiency by exploiting the 4-wide SIMD units.
Later, packets were adapted to the 32-wide SIMD
units on GPUs. Two different directions have been
followed in order to simulate on GPU the recursive
nature of hierarchical traversals. The first one is based
on stacks, which are implemented on shared memory.
Some of the papers included in this trend are (G
¨
unther
et al., 2007) for BVHs, and (Horn et al., 2007) for
KD-trees. The second approach introduces new links
in the tree to guide its traversal. Examples of these
stackless tracers are (Popov et al., 2007) and (Foley
and Sugerman, 2005) for KD-trees, and (Torres et al.,
2009) for BVHs. Recently, (Zlatuska and Havran,
2010) make a comparison of several GPU implemen-
TRAVERSING A BVH CUT TO EXPLOIT RAY COHERENCE
141

tations, including proposals of both tendencies.
Concerning the efficiency of explicit packets,
(Aila and Laine, 2009) question their practical inter-
est. Indeed, their paper shows that traversing each
ray independently is faster than traversing ray pack-
ets. Nevertheless, it only considers primary and sec-
ondary rays, which are arranged on the device ac-
cording to the image Z-order, thus they are implicitly
packed into geometrically coherent warps.
Geometric Coherence. The notion of geometric
coherence appears very often in the ray tracing bibli-
ography (Wald and Slusallek, 2001), and more espe-
cially in those papers concerning packet-based traver-
sals. Thus, we only mention recent papers that ana-
lyze different techniques for exploiting geometric co-
herence, among their main contributions. (Mansson
et al., 2007) present several geometric heuristics to or-
ganize newly spawn rays. Unfortunately, classifying
secondary rays on CPU takes too much time to make
them applicable. (Noguera et al., 2009) present a KD-
tree traversal for ray packets, using CPU’s SEE. Rays
are simply classified according to the signs of their di-
rections. (Boulos et al., 2007) propose several ways
of packing secondary rays. It shows a performance of
around 3x for the method that groups rays of the same
type vs. the single ray method.
Behavioral Coherence on CPU. Most of the pa-
pers concerning behavioral coherence can be classi-
fied in two groups. The first one is composed of those
works that use the acceleration structure as a refer-
ence to pack the rays into coherent packets. Among
them, (Pharr et al., 1997) describe a Monte Carlo ren-
derer that takes advantage of the cache units to reduce
memory traffic from disk. Furthermore, the rays get
enqueued in the voxels of a uniform grid. The sched-
uler subsystem is then responsible for starting the in-
tersection test of the rays in a queue against the ge-
ometry at the corresponding voxel, depending on the
information already cached.
Similarly, (Navratil et al., 2007) present another
technique to decrease the traffic between DRAM and
cache L2. Queues are now located at some nodes of a
KD-tree, called queue points. The subtrees related to
these nodes fit in cache L2, which is used to accelerate
the traversal of the rays in the queue along the subtree.
More recently, (Boulos et al., 2008) introduce the
quantitative notion of SIMD-coherence to measure
the utilization of the SIMD units. Specifically, it com-
putes the ratio between the number of active rays and
the packet size –which is fixed to 256 rays– to ex-
press how coherent the packet is. It then uses filter-
ing techniques to compact those packets whose ratio
drops below a threshold. This demand-driven reorder-
ing method gives the best results for diffuse path trac-
ing vs. glossy and perfect specular ray tracing.
The second group includes packing techniques
based on the operations that the rays demand, instead
of the nodes of the structure they pass through. The
aim of these proposals is to get the maximum of the
SIMD units. Thereby, (Wald et al., 2007) and (Grib-
ble and Ramani, 2008) present ray tracers in which
the rays are filtered to output those requiring the same
operations. Then, these operations are run over the
corresponding rays in a SIMD manner. The experi-
ments included in the former show a high SIMD uti-
lization, for ray streams of 64×64 at most. The per-
formance of the latter is predicted to 6-16 FPS, which
is subsequently improved to 15-32 FPS by separating
address and data processing (Ramani et al., 2009). In
both papers, the size of the ray streams is also up to
64×64.
Behavioral Coherence on GPU. (Garanzha and
Loop, 2010) is the first paper in explicitly exploiting
the notion of behavioral coherence on GPU, as we are
concerned. It firstly packs the rays using a geometri-
cal criterion that is based on the direction and the ori-
gin of the ray. In order to accelerate the classification,
the rays are previously transformed into hashing keys,
and then sorted by using fast GPU primitives (Harris
et al., CUDPP). Then, the frustum of each packet tra-
verses a BVH in breadth-first order. Finally, a list of
leaves is obtained per ray. The rays related to each
leaf are then split into packets and tested for inter-
section with the bounding volume of the leaf and its
triangles.
Finally, (Aila and Karras, 2010) present an ar-
chitecture similar to NVidia Fermi, that reduces the
memory traffic between DRAM and on-chip caches.
Its traversal is based on hierarchically located queue
points in the spirit of (Navratil et al., 2007).
3 BVH CUTS
A Cut of a BVH is a set of nodes C =
{n
1
, n
2
, . . . , n
N
|n
i
∈ BVH} such that for every leaf l
in the BVH, there exists a unique node n
j
∈ C satis-
fying l ∈ subtree(n
j
) (see Figure 2 for an example).
Thereby, a cut partitions the BVH into two disjoint
sets of nodes T (top) and B (bottom), with root ∈ T
and all the leaves belong to B –which is actually a
forest of N subtrees.
In order to exploit the behavioral coherence, rays
are classified into N sets of rays, one per node of the
cut. Specifically, a ray r is inserted into the set s
i
re-
lated to the node n
i
, whenever r intersects the bound-
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
142

1
2
4
8
9
5
10
16
17
11
3
6
12
13
18
19
7
14
15
4
5
12
13
7
Figure 2: Example of a BVH Cut.
1 i n : Cut C ; Ray R[N
R
] ;
2 out : f l o a t t
g
hit
[N
R
] ;
3 v ar :
4 f l o a t t
hit
[N
R
] ; b o o l mask[N
R
] ;
5 i n t id[N
R
] ; i n t max
R
;
7 f o r each r ∈ [1..N
R
] in p a r a l l e l do
8 t
g
hit
[r] = ∞ ;
10 / / For e a c h node i n t h e Cut
11 f o r e ach n
i
∈ C do {
12 / / I n t e r s e c t i o n o f a l l r a y s
13 / / w i t h t h e BV (n
i
) on GPU
14 f o r e a ch r ∈ [1..N
R
] in p a r a l l e l do {
15 t
hit
[r] = ∞ ;
16 mask[r] = test(r, BV (n
i
)) ;
17 }
18 / / Co m pa c tin g on GPU
19 compact(mask, id, max
R
) ;
20 / / T r a v e r s a l on GPU
21 traversal(R, id, max
R
, B
i
, t
hit
, t
g
hit
) ;
22 }
Figure 3: Traversing a BVH cut.
ing volume BV (n
i
) of n
i
. Observe that a ray can be-
long to different sets, thus, it can require the subse-
quent traversal of different subtrees. The classifica-
tion process can be compared to a breadth-first traver-
sal, since each ray spreads many tasks that are not
solved immediately, but later on. Finally, each set s
i
is split into packets that are behavioral coherent w.r.t.
the node n
i
. This splitting is trivial: a set of 32 con-
secutively rays are arranged into a packet. Moreover,
if the set s
i
yields a packet p, p is then related to the
BVH hanging from the node n
i
, which we will call B
i
.
Cut Traversing. Figure 3 shows the traversal
scheme for a BVH cut. It is mainly composed of three
stages. In the first one (lines 14–17) the array mask
is updated with the intersection test of each ray with
BV (n
i
). The second stage (function compact at line
19) removes the rays that did not pass the last intersec-
tion test by compacting the remaining ones. The array
id stores the indices of the rays that passed the test and
max
R
keeps the number of them. The third stage (line
21) is a traversal algorithm of the BVH B
i
in a depth-
first style. Any traversal algorithm is possible in this
stage and we have tested two GPU approaches as we
will detail in Section 5. The extraction order of the
rays to be traversed respects the order inside the array
R.
Traversing a cut leads to N classic traversals that
compute the nearest intersection point for each ray, in-
side the part of scene the corresponding B
i
covers. As
usual, we use distances to refer to points, and thus we
write t
hit
[r] to denote the intersection point related to
the (local) traversal of the current B
i
w.r.t. a given ray
r. Notice that these local traversals are run on GPU,
but sequentially launched from CPU. Therefore, the
final (global) distance for r, t
g
hit
[r], is computed as the
minimum among the values t
hit
[r] related to each B
i
.
Regarding the integration of pruning techniques,
two improvements can be considered. First, an intra-
B
i
pruning can be applied, and indeed is applied,
when launching the function traversal at line 21. The
current t
hit
[r] is then used during the traversal of B
i
to
rule out farther intersected nodes for r inside B
i
.
Second, an inter-B
i
pruning could be incorporated
at line 15 to suitably initialize the array t
hit
to the cur-
rent t
g
hit
, instead of ∞. Thus, this line would become
t
hit
[r] = t
g
hit
[r]. Again, the aim would be to take advan-
tage of the traversals that have been completed before
running the i-th iteration, i.e. the traversals of those
B
j
with j < i. Specifically, B
i
could be ruled out if
the current t
g
hit
[r] was less than the entry distance to
BV (n
i
). Nevertheless, the order among the B
i
that
leads to the best overall performance cannot be de-
termined in advance. So, we have not implemented
this inter-B
i
pruning and the results (Section 6) are an
upper bound, regardless how the B
i
are sorted.
4 CUT CREATION
In order to boost the efficiency of a cut, we must
compare the benefit from the behavioral coherence of
each packet to the overload due to the total number of
packet traversals the rays produce. Since both issues
are opposite, let us first analyze the two extremes.
The first one corresponds to the case in which the
cut is composed of the leaves of the BVH (C
leaves
).
The overload is then more expensive than the benefit,
because too many traversals arise: each ray requires a
test against each leaf whose bounding volume the ray
intersects. Hence, traversing the cut would degenerate
TRAVERSING A BVH CUT TO EXPLOIT RAY COHERENCE
143

1 Cut c r e a t e d e p t h ( node n , i n t d ) {
2 i f ( i s L e a f ( n ) ∨ d e p t h ( n ) == d )
3 r e t u r n {n} ;
4 e l s e {
5 Cut C
L
= c r e a t e d e p t h ( l e f t ( n ) , d ) ;
6 Cut C
R
= c r e a t e d e p t h ( r i g h t ( n ) , d ) ;
7 r e t u r n C
L
∪C
R
;
8 } }
9 Cut c r e a t e a r e a ( node n , f l o a t a ) {
10 i f ( i s L e a f ( n ) ∨ a r e a ( n ) < a )
11 r e t u r n {n} ;
12 e l s e {
13 Cut C
L
= c r e a t e a r e a ( l e f t ( n ) , a ) ;
14 Cut C
R
= c r e a t e a r e a ( r i g h t ( n ) , a ) ;
15 r e t u r n C
L
∪C
R
;
16 } }
Figure 4: Implementation of the structural heuristics for
building a Cut. Top: cut creation by DEPTH. Bottom: cut
creation by AREA.
into the inefficient brute force.
In the other extreme, the cut is just composed of
the root of the BVH (C
root
). Each ray then traverses
the whole BVH from its root in a depth-first way.
Thus, the usage of the cut is useless. To sum up, our
traversal method is not efficient in both extremes, and
a trade-off between the benefit and the overload of us-
ing a BVH cut should be found. Hence, we present
two different group of heuristics for building cuts,
which are later compared with respect to their per-
formance over usual scenes.
4.1 Structural Heuristics
The first group corresponds to structural heuristics,
because the resulting cuts are composed of those
nodes satisfying certain property that only depends
on the structure of the BVH. In our experiments we
have tested two properties that are respectively based
on the node’s depth (called DEPTH), and on the sur-
face area of its bounding volume (called AREA). Con-
cretely, the cuts consist of the nodes at a given depth
d for the DEPTH heuristic, while it is composed of the
first nodes from the root whose surface area falls be-
low a given threshold a for the AREA heuristic.
Figure 4 shows how to build a cut in function of
the property. Observe that a leaf l is immediately
added to the cut, although the property did not hold
for any node in the path from the root to l. This pre-
vents the traversal from ruling out parts of the scene.
1 Cut S i m u l a t e d A n n e a l i n g ( node root ) {
2 Cut currentCut = {root} ;
3 f l o a t currentTime = r e n d e r ( currentCut ) ;
4 Cut bestCut = currentCut ;
5 f l o a t bestTime = currentTime ;
6 Cut nextCut = e v o l v e ( currentCut ) ;
7 f l o a t nextTime =r e n d e r ( nextCut ) ;
8 i n t temp =MAX TEMP ;
10 f o r ( i = 0 ; i < NSteps ; i++){
11 f o r ( j = 0 ; j < NS t e p s pe r Te m p ; j + +){
12 / / A c c e p t a n c e t h r e s h o l d
13 f l o a t p = exp(
|currentTime−nextTime|
temp
) ;
14 i f ( ( nextTime < currentTime ) ∨ ( r a n d ( 0 , 1 ) < p ) ) {
15 currentCut = nextCut ;
16 currentTime = nextTime ;
17 / / Up d a te t h e b e s t T i m e
18 i f ( currentTime < bestTime ) {
19 bestTime = currentTime ;
20 bestCut = currentCut ;
21 }
22 }
24 nextCut =e v o l v e ( currentCut ) ;
25 nextTime = r e n d e r ( nextCut ) ;
26 } / / f o r j
27 temp = α · temp ;
28 } / / f o r i
30 r e t u r n bestCut ;
31 }
Figure 5: Implementation of Simulated Annealing for
building a cut.
4.2 Simulated Annealing
The cut construction can be formulated as an opti-
mization problem. Thus, our second group of heuris-
tics consists of methods that look for the minimum
solution inside a search space that is composed of all
possible cuts. The objective function to be minimized
is the render time a cut traversal requires. Accord-
ing to this formulation, many of the algorithms em-
ployed in combinatorial optimization can be used to
find the best cut. Nevertheless, searching for the best
cut turns to be unfeasible, as it usually happens for
many combinatorial optimization problems, hence we
focus on approximation algorithms. Among the ex-
isting algorithms, we have adapted the Simulated An-
nealing method (SA in the sequel), since it can be eas-
ily applied to these problems, due to its generic nature
(Zomaya and Kazman, 1999).
SA can be described as a randomized iterative im-
provement algorithm, since it does not only accept de-
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
144

creasing moves, regarding the given objective func-
tion, but it also tolerates increasing moves in order
to avoid getting trapped in local minima. Indeed, it
uses a probability function, that decreases as the exe-
cution advances, for accepting increasing moves. The
method asymptotically converges to a global mini-
mum, whenever certain conditions hold, concerning
the annealing schedule.
Figure 5 describes how to build a BVH cut us-
ing SA. Besides the current cut (currentCut), the al-
gorithm also holds another one (nextCut) that corre-
sponds to a random evolution of the former. These
two cuts advance together along the execution of
two nested loops: one for decreasing the control pa-
rameter temp (line 10) –the temperature used in the
original SA formulation– and another one for trying
many moves at the same temp (line 11). Regard-
ing increasing the render time, the algorithm accepts
those cuts whose acceptance threshold (line 13) is
greater than a uniform random value in [0,1] (line
14). If the nextCut is finally accepted, it is assigned to
currentCut (line 15) and the best cut is updated if re-
quired (lines 18–21). In any case, a new random evo-
lution is computed (line 24) and subsequently stored
in nextCut.
The function evolve generates a reachable cut
from currentCut by applying either the join or
the un f old operation. In the former, an inner
node n of the cut C is replaced by its two chil-
dren: un f old(C, n) = (C −{n})∪{le f t(n), right(n)},
whereas two sibling nodes l, r ∈ C of C are re-
placed by their father in the later: join(C, l, r) = (C −
{l, r}) ∪ { f ather(l)} In this function, one of these op-
erations is randomly chosen (if both are possible).
5 EXPERIMENTAL SETTINGS
Our application has been run on a NVIDIA GeForce
GTX 285 with 1GB of RAM. The test scenes are
FAIRYFOREST, CONFERENCEROOM, SPONZA and
SIBENIK (see Figure 1). The FAIRYFOREST scene
is open but a quadrilateral has been positioned as
a roof, preventing the rays from escaping from the
scene. All the images have been taken at a resolution
of 1024 × 1024.
The BVHs have been built by following the
Surface Area Heuristics (SAH) by (Goldsmith and
Salmon, 1987) and using the greedy top-down algo-
rithm by (Ize et al., 2007). To improve the overall per-
formance of the BVH, we have also applied the early
split clipping technique by (Ernst and Greiner, 2007).
So, before starting the construction, the bounding vol-
ume of each triangle is iteratively halved until its sur-
face area is lower than a certain threshold.
We have used path tracing (Kajiya, 1986) as our
ray tracing algorithm, and for the sake of conve-
nience, every surface of the scene is considered as
diffuse (i.e. with a constant BRDF). Hence, as soon
as a ray finds the nearest intersection point, a new ray
is spawned. Its origin is the intersection point and
its direction is randomly chosen over a virtual hemi-
sphere on the surface normal. We have considered the
cosine as the probability density function, i.e. those
points near the pole have more probability because it
depends on cos θ (where θ is the angular deviation of
the point from the pole). Since the number of rays
does not increase, we have an absolute control over
the memory that is actually allocated.
Each ray is bound to a persistent CUDA thread,
according to (Aila and Laine, 2009). The set of
rays whose associated threads are simultaneously
launched is called a generation. Generations are enu-
merated; the generation 0 is composed of the primary
rays, and the generation i is composed of the rays
spawn from the generation i − 1. The number of con-
sidered generations in this paper is fixed to 10. The
number of rays in a generation is the biggest one that
our implementation and our graphics card are able to
store: 8 MRays (= 8 · 2
20
rays). The primary rays are
spawned from a bidimensional array of 4096×2048.
Since the images are at a resolution of 1024 × 1024,
each subarray of 4 × 2 rays contains 8 samples for the
same pixel. When it is stored in memory, the bidi-
mensional array is flattened according to the Z-order
(Morton code).
In these settings, path tracing is specially suitable
for our experiments since no property can be assumed
in advance for the rays from generation 0 on (i.e. no
primary rays). As we will see in Section 6, the inco-
herency becomes maximal from generation 2 on.
We have used the linear congruential generator by
(Park and Miller, 1988) as random number generator
algorithm. It has a period of 2
31
− 2, which is greater
than the total amount of random numbers needed in
the tests, ensuring that each ray receives different ran-
dom numbers.
Our path tracer has been implemented with five
CUDA kernels: RayGenerator (RG), Test, Compact,
TraversalIntersection (TI) and Shader (SH). The algo-
rithm runs according to the following scheme. First,
the primary rays are spawned from a pinhole cam-
era, in the kernel RG. Then, in the kernel Test, the
rays are tested for intersection with a node n of the
cut. Next, the rays that passed the previous intersec-
tion test are compacted, in the kernel Compact. This
kernel is actually the primitive cudppCompact of the
CUDPP library by (Harris et al., CUDPP) and pre-
TRAVERSING A BVH CUT TO EXPLOIT RAY COHERENCE
145

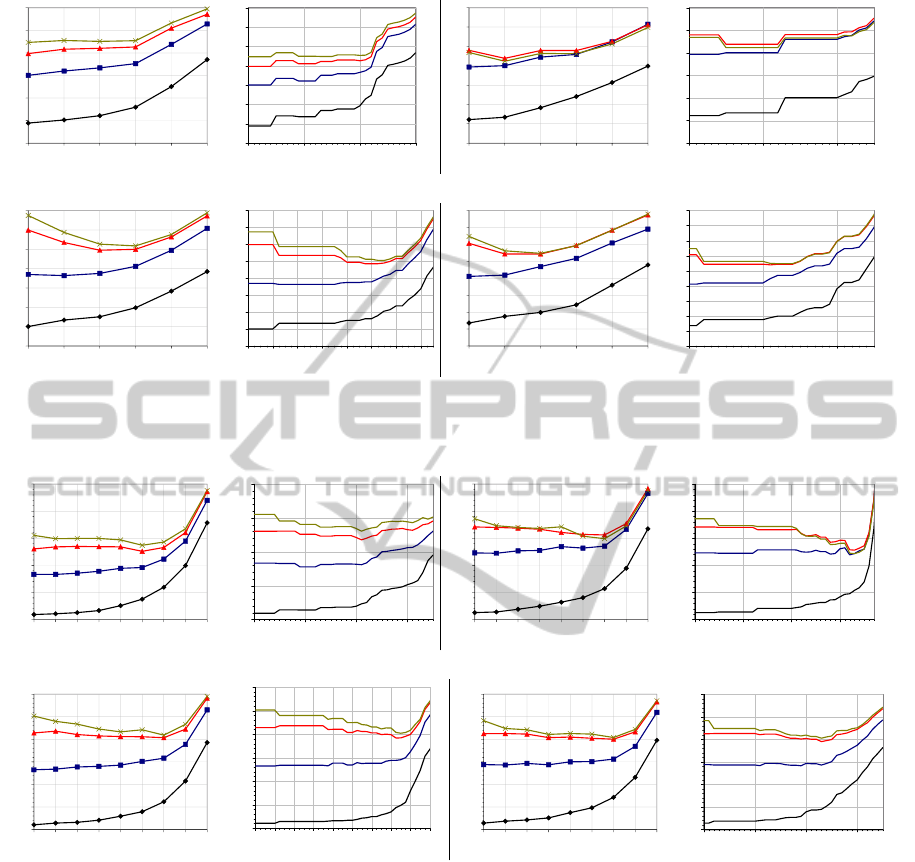
Conference Room Fairy Forest
0 1 2 3 4 5
Depth
0
100
200
300
400
500
600
10000200003000040000
Area
0
100
200
300
400
500
600
700
0 1 2 3 4 5
Depth
0
100
200
300
400
500
600
700
200003000040000
Area
0
100
200
300
400
500
600
Sibenik Sponza
0 1 2 3 4 5
Depth
0
100
200
300
400
500
600
700
600100014001800
Area
0
100
200
300
400
500
600
700
800
0 1 2 3 4 5
Depth
0
100
200
300
400
500
600
700
800
200003000040000
Area
0
100
200
300
400
500
600
700
800
900
Figure 6: Render times (in ms) measured for the four scenes with the traversal algorithm SINGLE by using structural cuts. The
colors are: black (generation 0), blue (generation 1), red (generation 2), green (generation 3).
Conference Room Fairy Forest
0 1 2 3 4 5 6 7 8
Depth
0
500
1000
1500
2000
2500
10000200003000040000
Area
0
500
1000
1500
2000
0 1 2 3 4 5 6 7 8
Depth
0
500
1000
1500
2000
2500
10000200003000040000
Area
0
500
1000
1500
2000
2500
Sibenik Sponza
0 1 2 3 4 5 6 7 8
Depth
0
500
1000
1500
2000
2500
3000
200600100014001800
Area
0
500
1000
1500
2000
2500
3000
0 1 2 3 4 5 6 7 8
Depth
0
500
1000
1500
2000
2500
3000
10000200003000040000
Area
0
500
1000
1500
2000
2500
3000
Figure 7: Render times (in ms) measured for the four scenes with the traversal algorithm PACKET by using structural cuts.
The colors are: black (generation 0), blue (generation 1), red (generation 2), green (generation 3).
serves the Z-order of the initial rays. Afterward, the
kernel TI finds the nearest intersection for every ray
by traversing the subtree hanging from n. The two
algorithms used for traversing a subtree are due to
(Aila and Laine, 2009). They are the persistent packet
and the persistent while-while and will be denoted by
PACKET and SINGLE, respectively. Finally, a new sec-
ondary ray is spawned over the hemisphere from the
nearest intersection in the kernel SH.
6 RESULTS
Structural Heuristics. Several structural cuts have
been built with different values for the parameter of
the DEPTH and AREA heuristics. The render time for
their traversal are depicted in Figure 6 for SINGLE and
in Figure 7 for PACKET. In the y-axis, the measured
render times (in ms) of the cut traversal are displayed.
In the x-axis, different values of the parameter are in-
cluded. Points of the same generation are joined in a
continuous line. However, only the first four genera-
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
146

Table 1: The percentage of saving in render time of the best cut built with the DEPTH heuristics w.r.t. C
root
. The numbers in
brackets are the depths of the best cuts.
SINGLE
Scene \ Gen. 0 1 2 3 4 5 6 7 8 9
Conf.Room 0.0(0) 0.0(0) 0.0(0) 0.0(0) 0.1(2) 1.4(2) 1.6(2) 2.0(2) 2.1(2) 2.1(2)
FairyForest 0.0(0) 0.0(0) 8.6(1) 9.6(1) 10.0(1) 9.7(1) 9.5(1) 9.4(1) 9.3(1) 9.0(1)
Sibenik 0.0(0) 1.5(1) 17.3(2) 23.2(3) 26.2(3) 28.0(3) 29.0(3) 29.8(3) 30.3(3) 30.6(3)
Sponza 0.0(0) 0.0(0) 10.4(2) 15.4(2) 17.1(2) 18.3(2) 19.0(2) 19.5(2) 19.8(2) 20.1(2)
PACKET
Scene \ Gen. 0 1 2 3 4 5 6 7 8 9
Conf.Room 0.0(0) 0.0(0) 3.3(5) 11.7(5) 7.4(5) 14.3(5) 9.0(5) 14.4(5) 9.0(5) 14.4(5)
FairyForest 0.0(0) 0.5(1) 8.6(6) 19.7(6) 16.7(6) 22.1(6) 18.0(6) 22.7(6) 18.1(6) 22.6(6)
Sibenik 0.0(0) 0.0(0) 4.9(6) 16.7(6) 13.8(6) 20.1(6) 17.0(6) 22.3(6) 17.8(6) 21.8(6)
Sponza 0.0(0) 0.6(1) 5.7(6) 15.4(6) 12.8(6) 17.9(6) 14.8(6) 19.7(6) 15.6(6) 20.0(6)
Table 2: The percentage of saving in render time of the best cut built with the AREA heuristics w.r.t. C
root
. The numbers in
brackets are the percentage of surface area related to the best cut w.r.t. the surface area of the root.
SINGLE
Scene \ Gen. 0 1 2 3 4 5 6 7 8 9
Conf.Room 0.0(100) 0.0(100) 0.0(100) 0.0(100) 0.8(75.3) 2.2(75.3) 2.4(75.3) 2.7(75.3) 2.4(75.3) 2.3(75.3)
FairyForest 0.0(100) 0.0(100) 8.6(99.4) 9.6(99.4) 10.0(99.4) 9.7(99.4) 9.5(99.4) 9.4(99.4) 9.3(99.4) 9.0(99.4)
Sibenik 0.0(100) 1.5(99.5) 18.9(59.7) 25.1(51.2) 27.9(51.2) 29.6(51.2) 30.6(51.2) 31.3(51.2) 31.7(51.2) 32.0(51.2)
Sponza 0.0(100) 0.0(100) 11.1(75.3) 15.4(72.7) 17.1(72.7) 18.3(72.7) 19.0(72.7) 19.5(72.7) 19.8(72.7) 20.1(72.7)
PACKET
Scene \ Gen. 0 1 2 3 4 5 6 7 8 9
Conf.Room 0.0(100) 6.5(86.4) 9.7(53.0) 16.0(53.0) 10.5(53.0) 16.6(53.0) 10.7(53.0) 16.3(53.0) 10.5(53.0) 15.7(53.0)
FairyForest 0.0(100) 2.8(22.7) 25.0(19.8) 34.6(19.8) 34.3(19.8) 39.1(19.8) 36.4(19.8) 40.3(19.8) 37.1(22.7) 40.9(22.7)
Sibenik 0.0(100) 0.0(100) 10.2(31.2) 19.6(28.4) 17.6(28.4) 23.5(31.2) 20.0(28.4) 25.1(28.4) 20.8(28.4) 24.9(28.4)
Sponza 0.0(100) 1.7(54.5) 8.2(44.1) 16.0(44.1) 13.6(44.1) 19.7(44.1) 15.4(44.1) 20.0(44.1) 16.8(44.1) 19.7(44.1)
Table 3: The percentage of saving in render time of the best cut found with Simulated Annealing w.r.t. C
root
. The numbers in
brackets (D/A) are: D, the averaged depth of the nodes in the cut; and A, the percentage of averaged surface area of the nodes
in the cut w.r.t. the surface area of the root.
SINGLE
Scene \ Gen. 0 1 2 3 4 5 6 7 8 9
Conf.Room 0.0 0.0 0.0 2.5 3.9 5.3 4.9 5.3 5.0 5.0
(0.0/100) (0.0/100) (0.0/100) (4.4/46.9) (4.5/43.2) (4.6/42.9) (4.0/49.0) (4.7/42.4) (4.1/48.8) (4.8/42.2)
FairyForest 0.0 5.9 17.1 16.3 15.8 14.7 14.0 13.4 12.8 12.4
(0.0/100) (5.0/17.9) (5.1/26.1) (4.4/31.2) (4.4/31.2) (4.4/31.2) (4.4/31.2) (4.4/31.2) (4.4/31.2) (4.4/31.2)
Sibenik 0.0 1.5 18.9 25.4 28.0 29.6 30.6 31.3 31.7 32.0
(0.0/100) (1.0/71.3) (2.8/46.9) (3.0/45.5) (3.0/45.5) (3.1/43.8) (3.1/43.8) (3.1/43.8) (3.1/43.8) (3.1/43.8)
Sponza 0.0 0.0 11.1 15.4 17.1 18.3 19.0 19.5 19.8 20.1
(0.0/100) (0.0/100) (1.6/68.2) (2.0/64.5) (2.0/64.5) (2.0/64.5) (2.0/64.5) (2.0/64.5) (2.0/64.5) (2.0/64.5)
PACKET
Scene \ Gen. 0 1 2 3 4 5 6 7 8 9
Conf.Room 0.0 21.8 31.5 37.0 33.3 37.2 32.1 36.0 30.7 34.5
(0.0/100) (6.1/26.8) (6.6/18.3) (6.6/17.4) (6.5/17.0) (6.5/17.4) (6.5/17.0) (6.5/17.4) (6.5/17.4) (6.4/17.7)
FairyForest 0.0 45.1 49.4 51.7 48.5 51.4 47.9 47.7 47.4 47.6
(0.0/100) (5.7/23.5) (5.8/20.0) (5.9/17.9) (5.8/16.6) (5.9/17.9) (5.9/17.8) (5.7/17.8) (5.9/17.9) (5.7/17.8)
Sibenik 0.0 9.3 14.8 21.4 18.8 23.7 20.3 24.5 20.9 24.9
(0.0/100) (5.8/28.0) (6.1/22.4) (6.2/21.3) (5.9/20.9) (6.0/20.9) (6.0/21.4) (6.0/21.8) (5.9/21.5) (6.0/21.8)
Sponza 0.0 3.4 14.8 24.1 21.5 26.6 22.9 27.3 23.2 27.5
(0.0/100) (5.5/32.0) (6.0/29.3) (6.4/28.2) (6.5/30.9) (6.4/29.9) (6.3/30.1) (6.2/30.3) (6.3/30.1) (6.3/29.9)
tions are showed for the sake of clarity, which gives
rise four curves per chart. The remaining ones have a
behaviour similar to generation 3.
The first (the leftmost) value of the parameter al-
ways corresponds to the structural value that builds
C
root
. Therefore, the first value of each curve cor-
TRAVERSING A BVH CUT TO EXPLOIT RAY COHERENCE
147

responds to the SINGLE or PACKET traversal of the
whole BVH plus an extra time due to filtering (around
10 ms according to our measures). Higher values in
DEPTH and lower values in AREA provoke an expo-
nential growth in render time, which is not included in
the charts. We have measured generations for differ-
ent random number seeds. The results are very similar
and only the charts for one seed are displayed on the
figures.
As it can be seen, the curves of a given generation
have a similar shape in every scene. The curves of
generation 0 (primary rays) and generation 1 do not
undergo any improvement w.r.t. the traversal of C
root
.
On the contrary, the generations 2 to 9 have a drop at
the beginning and an exponential increase after. The
depth of this valley depends both on the scene as well
as on the traversal algorithm.
The valley is deeper for PACKET than for SINGLE.
As (Aila and Laine, 2009) mention, SINGLE is more
efficient than PACKET for coherent (such as primary
rays) and non-coherent rays. This is due to the fact
that the memory bandwidth in modern GPUs is high,
and the bottleneck in PACKET is not the memory traf-
fic but the additional amount of traversed nodes.
Notice that, the minimum of each curve occurs
more to the left in SINGLE than in PACKET (i.e. in
shallower nodes or with bigger surface area). The
overload in both algorithms is the same, so the mem-
ory system must be the responsible for this difference.
If the packets are more coherent in SINGLE, the num-
ber of nodes read from memory does not vary, but the
texture caches are better used. On the contrary, if the
packets are more coherent in PACKET, the number of
nodes read from memory decreases, but the texture
cache usage is the same. Therefore, the curves show
that the improvement due to the diminishment of the
read nodes becomes relevant more to the right than
the benefit of cache.
For a given scene, the shape of the curves are very
similar in the DEPTH and AREA charts. This fact is
not surprising since deeper nodes have also smaller
surface areas.
The generations 0 and 1 have not an improvement
by the use of cuts. This is due to the fact that these
rays are very coherent and the improvement obtained
by launching more coherent packets is not enough to
exceed the overload.
Tables 1 and 2 summarize the best saving of the
figures. They include a column for each generation
that shows the percentage of saving of the best struc-
tural cut w.r.t. the performance of traversing C
root
.
Hence, it is computed by comparing the first value
of the corresponding curve with its minimum, that is,
through the expression
t
root
−t
min
t
root
, where t
min
and t
root
denote these two values. The most relevant savings
are 30.6%/32.0% (DEPTH/AREA) for SINGLE applied
to SIBENIK, while 22.7%/40.9% for PACKET applied
to FAIRYFOREST.
Simulated Annealing. The results can be seen on
Table 3. The parameters used are MAX TEMP=600,
NSteps=1000, NSteps per temp=1000 and α=0.99.
Observe that the percentage of saving is always
better than those related to structural cuts. This is nat-
ural since SA manages other cuts apart from structural
cuts.
For some scenes, there is a correspondence be-
tween the averaged depth of the best SA cut and the
best structural-depth cut (e.g. SIBENIK with SINGLE).
However, this cannot be generalized to all scenes.
7 DISCUSSION AND FUTURE
WORK
The benefit of the usage of cuts is consequence of the
fact that the overload due to filtering is less than the
improvement obtained by traversing more coherent
rays. It is an open issue if this technique is also appli-
cable to CPU ray tracers, other rendering algorithms
(such as bidirectional path tracing), other non-diffuse
surfaces (such as specular or glossy), and other accel-
eration structures (such as KD-trees).
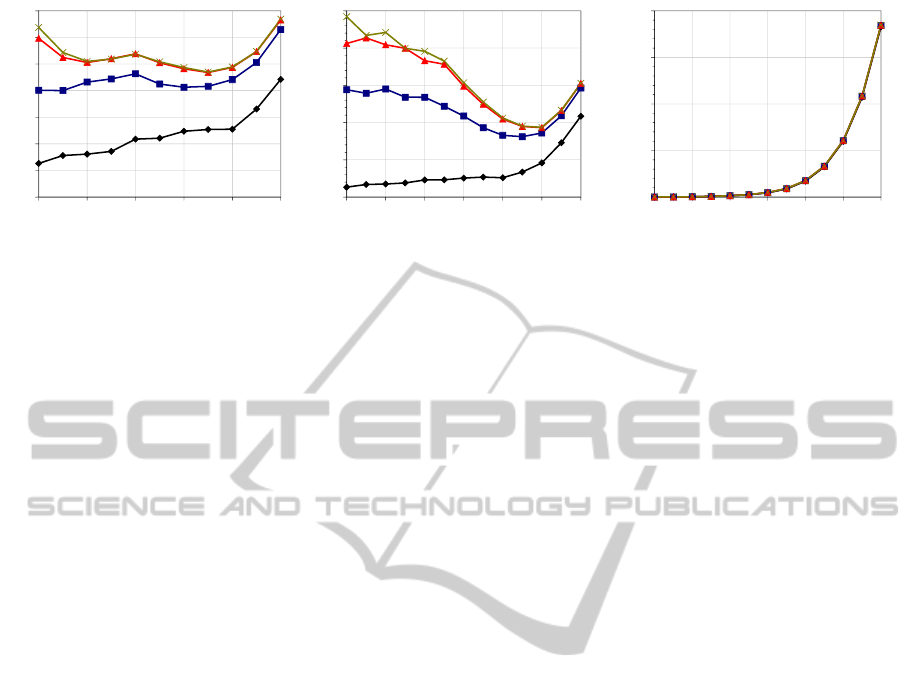
Figures 8a and 8b show the render time for only
the kernel TI concerning SINGLE and PACKET respec-
tively. Observe that the curves of highly incoherent
generations (red and green) present a minimum show-
ing that a cut at a certain depth leads to a relevant
improvement. Nevertheless, the overload due to fil-
tering grows exponentially (Figure 8c). This is why
the minima in Figures 6 and 7 are shifted to the left.
It is necessary to study ways of making the most of
that coherence or diminishing the overload.
In order to diminish the overload (number of fil-
ters), two cuts C1 and C2 can be used. The nodes of
C1 are used to filter the rays whereas the nodes of C2
are used to traverse the scene. Each node n ∈ C1 is
linked to a set of nodes {n
0
1
, . . . , n
0
N
} ⊆ C2, such that
the nodes n
0
i
are descendants of n. Thus, the number
of filters are fewer than the amount of nodes in C2
(since |C1| ≤ |C2|). The inconvenient is that the rays
launched for traversal are more incoherent. We did
not obtain successful results and this technique was
dismissed.
Nowadays, there already exist cards with more
DRAM capacity than the one used in this paper (e.g.
the Tesla C2070 has 6 GB). A bigger amount of mem-
ory would allow more rays to be stored and traversed
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
148

0 2 4 6 8 10
Depth
0
100
200
300
400
500
600
700
0 2 4 6 8 10 12
Depth
0
500
1000
1500
2000
2500
0 2 4 6 8 10 12
Depth
0
5000
10000
15000
20000
(a) (b) (c)
Figure 8: (a) Render time without overload (only TI) for SPONZA and SINGLE; (b) render time without overload (only TI) for
SPONZA and PACKET; (c) overload for the subfigures (a) and (b).
in parallel. Thus, the coherence would be higher and
better results would be expected. However, this anal-
ysis should be experimentally evaluated.
In this paper, the russian roulette method for fin-
ishing a path has not been implemented. On the con-
trary, every ray keeps alive till generation 9. It is ex-
pected that high generations will not behave similarly
if the size of their populations is different.
The time used to build our cuts are not included
in the results, since the construction is considered as
a preprocess. It would be worth to study methods that
quickly find an effective cut in order to execute the
construction during rendering.
8 CONCLUSIONS
In this paper we have studied how to deal with the
ray incoherence that naturally arises in path tracing-
based systems. In order to improve the BVH traver-
sal of a great amount of incoherent rays, we split the
BVH structure into a forest of disjoint subtrees, called
Cut, that will be used to group the rays that are suc-
cessively generated. Each subtree is then traversed
by state-of-the-art algorithms: persistent while-while
and persistent packet. We experimentally show that,
despite the overload of filtering all the rays for each
subtree, the subsequent traversal of all these subtrees
results faster than traversing the whole BVH. The rea-
son is that the rays traversing a subtree are more co-
herent according to the behavioral criterion.
We have presented two kinds of heuristics for
building a BVH cut. The first one corresponds to
structural properties such as the node’s depth and the
surface area of the bounding volume of the node. For
the second one, the construction of the cut is formu-
lated as an optimization problem, and the Simulated
Annealing method is applied to build the best cut. Our
experiments show that using a cut results in a signifi-
cant improvement w.r.t the classic traversal of the
BVH. Moreover, this improvement increases accord-
ing to the incoherent measure of the ray generation.
The saving depends on the scene, and also on the
traversal algorithm (persistent while-while / persistent
packet). For example, for the FAIRYFOREST scene,
the best saving times for DEPTH are 10.0% / 22.7%
(SINGLE / PACKET), for AREA are 10.0% / 40.9%, and
for Simulated Annealing are 17.1% / 51.7%.
ACKNOWLEDGEMENTS
This paper has been supported by the Spanish
projects CCG10-UCM/TIC-5476 and BSCH-UCM
GR58/08-921547.
REFERENCES
Aila, T. and Karras, T. (2010). Architecture considera-
tions for tracing incoherent rays. In Proceedings of
the High-Performance Graphics 2010.
Aila, T. and Laine, S. (2009). Understanding the efficiency
of ray traversal on GPUs. In Proceedings of High-
Performance Graphics 2009, pages 145–149.
Boulos, S., Edwards, D., Lacewell, J. D., Kniss, J., Kautz,
J., Wald, I., and Shirley, P. (2007). Packet-based Whit-
ted and Distribution Ray Tracing. In Proceedings of
Graphics Interface 2007, pages 177–184.
Boulos, S., Wald, I., and Benthin, C. (2008). Adaptive
ray packet reordering. Symposium on Interactive Ray
Tracing, 0:131–138.
Ernst, M. and Greiner, G. (2007). Early split clipping for
bounding volume hierarchies. In Proceedings of the
2007 IEEE Symposium on Interactive Ray Tracing,
pages 73–78.
Foley, T. and Sugerman, J. (2005). KD-tree acceleration
structures for a GPU raytracer. In HWWS’05 Confer-
ence on Graphics Hardware, pages 15–22.
TRAVERSING A BVH CUT TO EXPLOIT RAY COHERENCE
149

Garanzha, K. and Loop, C. (2010). Fast ray sorting and
breadth-first packet traversal for GPU ray tracing. In
Eurographics, volume 29.
Goldsmith, J. and Salmon, J. (1987). Automatic creation
of object hierarchies for ray tracing. IEEE Computer
Graphics and Application, 7(5):14–20.
Gribble, C. P. and Ramani, K. (2008). Coherent ray trac-
ing via stream filtering. In IEEE/Eurographics Sym-
posium on Interactive Ray Tracing, pages 59–66.
G
¨
unther, J., Popov, S., Seidel, H.-P., and Slusallek, P.
(2007). Realtime ray tracing on GPU with BVH-based
packet traversal. In Proceedings of the Eurographics
Symposium on Interactive Ray Tracing, pages 113–
118.
Harris, M., Owens, J. D., Sengupta, S., Tzeng,
S., Zhang, Y., Davidson, A., and Satish, N.
CUDA data parallel primitives library (CUDPP).
http://gpgpu.org/developer/cudpp.
Horn, D. R., Sugerman, J., Mike, H., and Hanrahan, P.
(2007). Interactive KD-tree GPU raytracing. In
I3D’07: Proceedings of the symposium on Interactive
3D graphics and games, pages 167–174.
Ize, T., Wald, I., and Parker, S. G. (2007). Asynchronous
BVH construction for ray tracing dynamic scenes on
parallel multi-core architectures. In Proceedings of
the Eurographics Symposium on Parallel Graphics
and Visualization, pages 101–108.
Kajiya, J. T. (1986). The rendering equation. SIGGRAPH
Computer Graphics, 20(4):143–150.
Mansson, E., Munkberg, J., and Akenine-Moller, T. (2007).
Deep coherent ray tracing. In RT ’07: Proceedings of
the 2007 IEEE Symposium on Interactive Ray Trac-
ing, pages 79–85.
Navratil, P. A., Fussell, D. S., Lin, C., and Mark, W. R.
(2007). Dynamic ray scheduling to improve ray co-
herence and bandwidth utilization. In RT ’07: Pro-
ceedings of the 2007 IEEE Symposium on Interactive
Ray Tracing, pages 95–104.
Noguera, J. M. and Ure
˜
na, C. and and Garc
´
ıa, R. J. (2009).
A vectorized traversal algorithm for ray-tracing. In
International Conference on Computer Graphics The-
ory and Applications (GRAPP 2009), pages 58–63.
Park, S. K. and Miller, K. W. (1988). Random number gen-
erator: Good ones are hard to find. Communications
of the ACM, 31(10):1192–1201.
Pharr, M., Kolb, C., Gershbein, R., and Hanrahan, P. (1997).
Rendering complex scenes with memory-coherent ray
tracing. In SIGGRAPH ’97: Proceedings of the 24th
annual conference on Computer graphics and inter-
active techniques, pages 101–108.
Popov, S., G
¨
unther, J., Seidel, H.-P., and Slusallek, P.
(2007). Stackless KD-tree traversal for high perfor-
mance GPU ray tracing. Computer Graphics Forum
(Proceedings of Eurographics), 26(3):415–424.
Ramani, K., Gribble, C. P., and Davis, A. (2009). Stream-
ray: A stream filtering architecture for coherent ray
tracing. In Internationa Conference on Architectural
Support for Programming Languajes and Operating
System, pages 325–336.
Torres, R., Mart
´
ın, P. J., and Gavilanes, A. (2009). Ray cast-
ing using a roped BVH with CUDA. In Proc. Spring
Conference on Computer Graphics, pages 107 – 114.
Wald, I., Benthin, C., Wagner, M., and Slusallek, P. (2001).
Interactive rendering with coherent ray tracing. In
Computer Graphics Forum (Proceedings of Euro-
graphics’01), volume 20, pages 153–164.
Wald, I., Gribble, C. P., Boulos, S., and Kensler, A. (2007).
SIMD Ray Stream Tracing - SIMD Ray Traversal with
Generalized Ray Packets and On-the-fly Re-Ordering.
Technical Report UUSCI-2007-012.
Wald, I. and Slusallek, P. (2001). State of the art in inter-
active ray tracing. In State of the Art Reports, EURO-
GRAPHICS 2001, pages 21–42.
Zlatuska, M. and Havran, V. (2010). Ray tracing on a GPU
with CUDA – comparative study of three algorithms.
In Proceedings of WSCG’2010, communication pa-
pers, pages 69–76.
Zomaya, A. and Kazman, R. (1999). Handbook of Algo-
rithms and Theory of Computation, chapter Simulated
Annealing Techniques, pages 37.1–33.19. CRC Press.
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
150