
AUTOMATED TUNING OF PARAMETERS FOR THE
SEGMENTATION OF FREEHAND SKETCHES
D. G. Fernández-Pacheco
1
, F. Albert
2
, N. Aleixos
2
, J. Conesa
1
and M. Contero
2
1
Departamento de Expresión Gráfica, Universidad Politécnica de Cartagena, Cartagena, Spain
2
Instituto Interuniversitario de Investigación en Bioingeniería y Tecnología Orientada al Ser Humano
Universidad Politécnica de Valencia, Valencia, Spain
Keywords: Sketching, Segmentation, Simulated annealing.
Abstract: One of the main problems in the segmentation of freehand sketches is the difficulty of tuning the parameters
involved in the process. Commonly, these parameters are chosen empirically from the observation of
segmentation results in training sets. However, this approach rarely gets the best set of parameters,
especially when the parameters depend on each other. This work presents an optimization algorithm, based
on the simulated annealing technique, which tunes the segmentation parameters to improve segmentation
results. The tuning of parameters has been formulated as an optimization problem where the cost function is
expressed as the number of errors in the segmentation of a training set. Errors are determined comparing the
computer segmentation with the correct one defined during the design of the shapes of the training set.
Experimental work used 177 samples of 20 different shapes, achieving a performance ratio of 97.0% for the
correct segmentation after tuning of parameters.
1 INTRODUCTION
Sketching is a useful tool which plays an important
role in the new product development process.
Different types of sketches are used in that process.
Prescriptive or analytical sketches (Varley &
Company, 2008) are hand-made technical drawings
which contain detailed information describing a final
design. They contain a full set of views
complemented by symbolic information conveyed
through standardized symbols, but they do not need
to be geometrically perfect.
Computer processing of this kind of sketches and
its integration on computer aided design applications
still present many issues to be solved. With this aim,
some research groups are exploring new paradigms
for sketch analysis and understanding like agent-
based architectures (p.e. Juchmes, Leclercq & Azar,
2005; Azar, Couvreury, Delfosse, Jaspartz &
Boulanger, 2006; Casella, Deufemia, Mascardi,
Costagliola & Martelli, 2008; Fernández-Pacheco,
Aleixos, Conesa & Contero, 2009; Flasinski, Jurek
& Myslinski, 2009; Fernández-Pacheco, Conesa,
Aleixos, Company & Contero, 2009). In this
context, our research group is performing the
recognition process through a two level agent
architecture, where "primitive agents" are in charge
of the syntactic recognition, and "combined agents"
carry out the semantic recognition using contextual
information.
The reliability of primitive agents strongly
depends on the robustness of the employed
segmentation algorithm and its parameterization. So,
one of the main problems in the segmentation of
freehand sketches is the difficulty of tuning the
parameters involved in the process. The way of
drawing is different for each user and even if the
sketched figures are quite similar, the segmentation
can vary. Commonly, the initial or default values of
the parameters to control the segmentation are
chosen empirically from previous experience, but
this rarely gets the best set of parameters, especially
when the parameters are interrelated. These
misclassifications are usually due to the difficulty of
tuning the whole set of parameters altogether. In
order to overcome this limitation this paper proposes
an optimization approach using a simulated
annealing (SA) algorithm (Kirkpatrick, Gelatt &
Vecchi, 1983) to tune the segmentation parameters.
There are some examples of application of
321
G. Fernández-Pacheco D., Albert F., Aleixos N., Conesa J. and Contero M..
AUTOMATED TUNING OF PARAMETERS FOR THE SEGMENTATION OF FREEHAND SKETCHES.
DOI: 10.5220/0003363903210329
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 321-329
ISBN: 978-989-8425-45-4
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
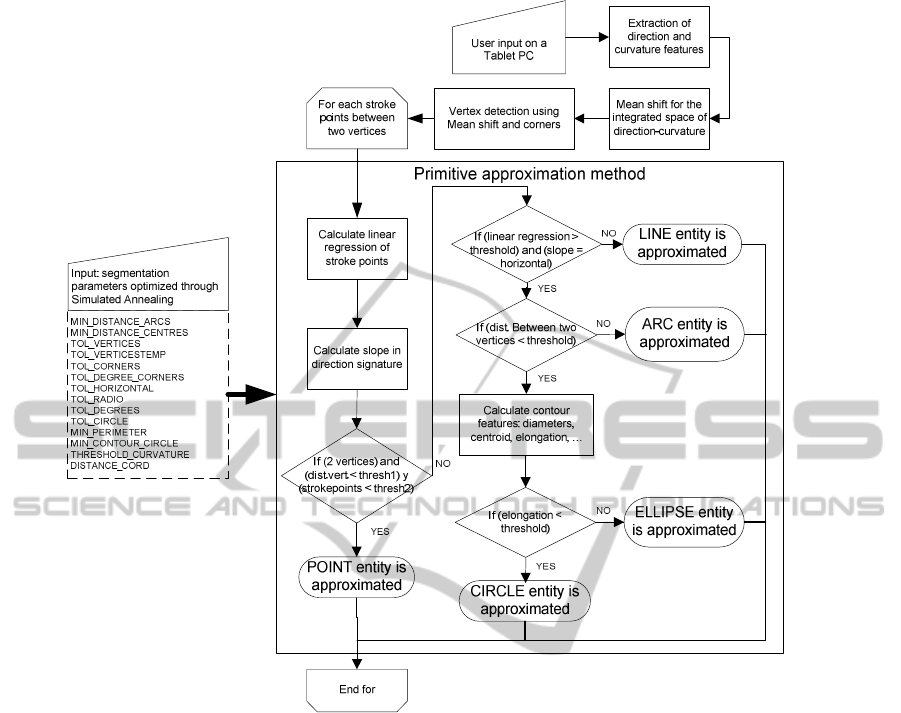
Figure 1: Flow chart of the segmentation algorithm (segmentation parameters listed in Table 1).
optimization algorithms to computer vision
problems: Taylor and Wolf (2004) applied an
optimization approach to improve the settings of
their text detection algorithm in images and video
sequences. Mbogho and Scarlatos (2007) used a
genetic algorithm to tune the colour thresholds to
minimize the effects of lighting variations on the
recognition of colored visual tags. Gelasca,
Salvador and Ebrahimi (2003) proposed a
framework for an intuitive tuning of parameters in
image and video segmentation algorithms. Other
applications to processes related to computer vision
have been developed by Mukerjee et al. (1997),
Davis et al. (2008), or Iakovidis et al. (2007).
The article is organized in the following way:
first the segmentation process is explained
(including the sketch correction, the vertices
detection procedure and the primitive approximation
method), secondly the implementation of the
optimization process by means of the simulated
annealing algorithm is detailed, and finally,
experimental work and results are given.
2 THE SEGMENTATION
ALGORITHM
Our application SegSGeo (Segmenting Sketched
Geometry) analyzes a stroke when a pen up event is
encountered, and fits the sketch into an outlined
sketch (poly-line). Its structure is shown in figure 1
and the procedure consists of five steps:
1. Direction and curvature signatures of the
stroke are calculated.
2. The mean shift (smoothing technique)
procedure is applied to the two previous
signatures (Yu, 2003).
3. Changes in direction of strokes are detected,
and vertices are fixed using peaks in
smoothed curvature signature.
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
322

4. A refinement of vertices is carried out when
their path length is less than a desired
threshold fixed empirically.
5. Finally, the type of each entity between a pair
of vertices is decided by means of a primitive
approximation method. Supported entities are
lines, arcs, circles and ellipses, and its type is
decided by looking into the direction
signature before Mean shift is applied, and
analyzing the points corresponding to that
piece of the stroke.
2.1 Extraction of Direction
and Curvature Signatures
The stroke is composed by a set of coordinates (x,y)
in an interval of pen-down and pen-up events. In
such a stroke, there are two visual features which
can guide recognition: direction and curvature. The
direction gives the angles between two consecutive
pairs of coordinates in the range [-π,π]. The
curvature gives the arctangent of the direction
between two consecutive points, to inform on how
opened or closed such piece of the stroke is.
2.2 Finding Vertices
Mean shift procedure (1) has been used to smooth
the collected stroke, since it has proven to give good
results in analyzing clusters in feature space, and in
eliminating noise (Yu, 2003).
,...2,1,
'
'
1
2
1
2
1
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
∑
∑
=
=
+
j
h
xz
k
h
xz
kx
z
n
i
ij
n
i
ij
i
j
(1)
In order to apply this procedure to the two-
dimensional direction-curvature joint space, we will
consider x
i
, i=1,2…n (where n is the number of
points in the direction-curvature joint space) as the
input vector of the mean shift procedure, that is, the
joint space d
i
and c
i
; and z
i
as the output vector of
smoothed discrete values of direction and curvature,
that is, the new direction and curvature signatures
after smoothing. The term k’ is the derivative of the
profile of Gaussian kernel k(x) = exp(−x / 2), and the
term h is the “bandwidth”, that is, the smoothing
parameter, which has been adjusted to h
d
and h
c
,
depending on direction and curvature respectively.
The smoothed curvature signature guides us to
find vertices in the stroke when seeking for local
maxima values, that is, where curvature changes
considerably (peaks in curvature signature figure
2c). The vertices seek routine finishes merging two
consecutive vertices when the path length between
them is lower than a threshold.
In the example of figure 2, six vertices are found,
and the first entity is approximated to an arc (arc
through 3 points: initial, final and middle of the first
section of the stroke) and the rest of entities to lines.
This has been achieved looking into both, the
original direction signature before mean shift
procedure between each two consecutive vertices,
and the correlation with the linear regression of the
stroke points of each entity, what is done by means
of the primitive approximation method.
Freehand sketch composed of 1
arc and 4 lines (in this order) A)
Direction signature
Curvature signature B)
Result of segmentation
process D)
Direction signature after
smoothing
Curvature signature after
smoothing C)
Figure 2: Example of a sketched figure.
2.3 Primitive Approximation Method
and Segmentation Parameters
The original direction signature and the correlation
of the stroke points from their linear regression are
used to identify the primitive entities composing a
stroke. If the features of the corresponding stroke
points are analyzed and the direction signature is
found to be horizontal, then that section of the stroke
is approximated to a line; otherwise it can be
approximated to an arc, circle or ellipse (see Figure
3). To approximate the section to an arc entity, the
direction signature must be inclined and the vertex
ends V
i
and V
f
separated, thus the section is fitted to
an arc by three points V
i
, V
f
and s. If the vertices are
close, the section is approximated to a circle or
ellipse depending on the elongation (quotient
between major R and minor r radius).
The segmentation process is controlled by 14
parameters, listed in Table 1. For each parameter a
range of values from previous observations has been
established (range column).
AUTOMATED TUNING OF PARAMETERS FOR THE SEGMENTATION OF FREEHAND SKETCHES
323

Table 1: Parameters of the segmentation and its initial range.
Parameter Description Range
MIN_DISTANCE_ARCS Distance between the two ends of an arc [0,50]
MIN_DISTANCE_CENTRES* Distance between the centers of two consecutive arcs [0,100]
TOL_VERTICES Tolerance for the distance between two consecutive vertices [0,30]
TOL_VERTICESTEMP Involved in the seek for local maximums and minimums [1,30]
TOL_CORNERS Distance from a point to both sides to calculate the angle of a corner [1,20]
TOL_DEGREE_CORNERS Threshold to considerate a corner as a vertex [1,60]
TOL_HORIZONTAL Tolerance for a horizontal slope [0,0.05]
TOL_RADIO* Tolerance for large values of radio [200,600]
TOL_DEGREES* Tolerance for the orientation of two consecutive lines [0º,30º]
TOL_CIRCLE Tolerance for the quotient of diameters to distinguish a circle from ellipse [0.3,0.8]
MIN_PERIMETER Minimum length for a line or arc [2,10]
MIN_CONTOUR_CIRCLE Minimum contour for circle or ellipse [30,200]
THRESHOLD_CURVATURE Tolerance for vertices in order to consider the stroke a circle or ellipse [0.1,0.5]
DISTANCE_CORD Arc length to help the decision of an arc or a line [20,300]
* Refinement parameters.
Mid
p
oint
V
i
V
f
Intersection
p
oint
s
α+π/2
α
r
a) Fitting a stretch of sketch to an arc.
V
i
V
f
α+π/2
α
r
R
b) Fitting a stretch of sketch to a circle/ellipse.
Figure 3: Parameters calculated for arcs/circles/ellipses entities.
3 TUNING OF SEGMENTATION
PARAMETERS
The steps for tuning the parameters of the
segmentation process consist of four main parts:
1. Definition of the initial range of values for
each segmentation parameter based on
previous experience.
2. Automatic tuning of parameters inside their
initial range using a simulated annealing
algorithm.
3. Definition of the definitive range of values
for each segmentation parameter, analyzing
the behaviour of each parameter when the
rest of parameters are fixed to their optimal
values.
4. Automatic tuning of parameters inside their
definitive range using a simulated annealing
algorithm.
The quality of the obtained segmentation is
evaluated by means of a cost function (2) that
returns a real value (cost) from a set of n
segmentation parameters P = {p
1
, p
2
, ... p
n
}.
ℜ
→Pc :
(2)
The cost value for a set of parameters is defined
as the ratio of bad segmented shapes using this set of
parameters. A library of sketched figures and their
correct segmentation has been developed in order to
implement the cost function (examples at Figure 4).
The correct or ideal segmentation has been
previously defined by consensus by the research
team of this work. The criteria applied to define a
well segmented shape are based on an all-or-nothing
accuracy, that is, a shape is well segmented if:
The number of vertices must match the
ideal segmentation.
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
324

The type of fitted primitives connecting the
vertices must match the intended primitives
of ideal segmentation.
Sketched shape and correct
segmentation
Result of
segmentation
Primitives=1 line, 1 arc, 2 lines
Primitives=1 arc, 2
lines
Primitives=2 lines, 2 arcs, 1
line
Primitives=3 lines, 1
arc, 2 lines
Figure 4: Examples of missegmentations. (Intended
segmentation vertex ( ), recognized vertex ( ) and
recognized primitive in red color).
3.1 Tuning of Parameters using a
Simulated Annealing Algorithm
The next step carried out to determine the optimal
range of the segmentation parameters is
implemented by a simulated annealing algorithm
(Kirkpatrick, Gelatt and Vecchi, 1983). The SA
algorithm is shown in figure 5 and described below.
The parameters involved in the SA algorithm can be
classified as generic or specific.
The “generic parameters” or "annealing
schedule" control the operation of the algorithm.
They are:
Initial Temperature: initial value of temperature
at the beginning of the SA process. It is
calculated using the following expression
(Kouvelis et al., 1992):
()
()
1
0
0
ln
−
+
Δ
=
χ
C
T
(3)
where
()
+
ΔC
is the mean value of the cost
increment associated to those displacements
with an increment in the cost function. In our
particular case, the tests performed show that
for 100 displacements,
()
5.1≈Δ
+
C
. Where χ
0
is
the expected initial coefficient of acceptance (χ
is the rate of accepted displacements with
respect to the total number of attempts). Using
a typical value of this coefficient in the
literature (χ
0
=0.75), the resulting value for
initial temperature is T
0
≈5.
Cooling Schedule: indicates how temperature
varies from two different steps. The more
common form consists of a potential cooling
(faster with high temperatures):
mm
TkT
⋅
=
+1
(4)
where m is the current temperature step, and k
is the cooling coefficient. A rapid cooling
(small values of k) causes a quick fall in the
cost, but if it is too fast, the SA may exit
without reaching good solutions. Moreover, a
slow cooling down makes the cost function to
have ups and downs (high cost displacement
are allowed) but increases the number of
iterations (the time required) and the
probability of finding the optimal solution. A
value of 0.5 has shown a good compromise
with respect to cost and speed.
END
Frozen
system
?
Change
temperature
?
?
> random(0,1)
?
Accept new solution
n
s
= n
s
+ 1
Generating new solution
m = n
s
= n = 0
c
0
Solution j-1 Solution j
c= c(P
j
)-c(P
j-1
)
e
c
T
yes
yes
no
no
Initialization
Calculate To
n = n + 1
TkT
mm1
mm1
n
s
= n = 0
Figure 5: SA algorithm.
Balance Criterion (change temperature): it
decides when the temperature must go
AUTOMATED TUNING OF PARAMETERS FOR THE SEGMENTATION OF FREEHAND SKETCHES
325
downhill to the next step using this logical
condition:
(
)
()
max
max
nnORnn
ss
>>
(5)
Where:
o n
s
is the number of successful displacements
in the present temperature step.
o n
s
max
is the maximum number of successful
displacements in a temperature step. Usually
this number is determined according to the
size of the space of solutions. In this problem,
the used value is the number of parameters to
optimize, in this case with 14 parameters,
n
s
max
=14.
o n is the number of attempted displacements in
the present temperature step.
o n
max
is the maximum number of attempted
displacements in a temperature step, and
usually is proportional to the n
s
max
value. In
the current context, n
max
= 2· n
s
max
, so n
max
=28.
Freezing Criterion: it is the stop criterion that
terminates the SA process:
()
(
)
max
min
mmOR ><
χχ
(6)
The freezing condition can be accomplished
when the temperature has experimented a
specific number of downhill moves (m
max
), or
when the coefficient of acceptance is very low
(χ = n
s
/ n), where:
o
χ
min
is the minimum coefficient of
acceptance, in this case 1% is the selected
value.
o m
max
is the maximum allowed number of
temperature steps, in this case the selected
value is 50.
The specific parameters of the SA in the context
of our problem are:
The Space of Solutions P, that in this case
corresponds to the 14 parameters used for
segmentation (see table 1):
P = {p
1
, p
2
, ... p
14
}
(7)
A displacement mechanism for choosing a
solution nearby the current one. For each
parameter pi to optimize in the iteration j, its
value is obtained from its previous value (from
the iteration j-1) as follows:
ijijiij
pp
ξδ
⋅+=
− )1(
(8)
Where p
i
∈
[p
i
min
, p
i
max
], δ
i
=α·(p
i
max
- p
i
min
),
and α is the maximum displacement ratio (α =
0.1 provided a good performance in the current
problem).
ξ
ij
is a random number in the range
[−1,1], obtained for each parameter in each
iteration.
The cost function
ℜ→Pc :
that gives a value
that must be minimized. For a training set of nt
sketched figures this function is defined as:
c = n
m
/ n
t
(9)
Where n
m
is the number of mistakes
corresponding to those bad segmented shapes
applying the criterion defined at the beginning
of section 3.
The best solution obtained during the
optimization process is stored, in order to avoid
situations where the final solution does not
correspond to the optimal one.
0
10
20
30
40
50
60
70
80
90
100
0 100 200 300 400 500
Figure 6: Cost and temperature evolution in a SA process.
3.2 Individual Parameter Adjustment
After the first simulated annealing step, in order to
establish the definitive range for a specific parameter
p
i
we have fixed the rest of the parameters to their
optimal value (obtained from the previous simulated
annealing step), and the cost is obtained with the
parameter p
i
ranged in its whole initial range (and
expanded if it is necessary). The definitive range is
fixed centring it in the optimal value obtained from
the process and expanded or compressed if it is
necessary.
Figure 7 shows the initial or default range for the
segmentation parameter TOL_VERTICES fixed
from expertise. As notice, the value of this
parameter for the minor cost function is beyond the
right value 30, so best results in segmentation are
never reached. Figure 8 shows the corrected range
for this parameter. Now, the optimal value is
Best solution
Local minimum
Cost / Temperature
Iterations
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
326

centered in the range so better results in
segmentation can be achieved.
So, the value of the parameter for the lowest
function cost has been centered in a range, and its
width has been fixed in order to avoid the function
cost increase more than a percentage. This width is
variable for each parameter.
0
5
10
15
20
25
30
35
40
45
50
0102030
Initialrange:[0,30]
Figure 7: Initial range for parameter TOL_VERTICES.
0
5
10
15
20
25
30
35
40
45
50
0 1020304050607080
Definitiverange:[0,80]
Figure 8: Definitive range for parameter TOL_VERTICES
after the correction process.
When all the ranges have been adjusted, the
second simulated annealing step provides the final
segmentation parameter values.
4 EXPERIMENTAL WORK
The segmentation process has been applied to a set
of 177 samples of 20 different sketched figures
(including circle and ellipse) collected from 3 users
and stored in a DB. Each user drew 3 samples of
each figure, and 3 figures with poor quality were
discarded.
Figures 9 and 10 show some examples of
sketched figures segmented using the parameters
optimized with the SA algorithm.
Sample01
Sample02 Sample03
Sample04
Sample05 Sample06
Sample09
Sample10 Sample11
Figure 9: Examples of sketched figures used in the tests
including only lines.
Sample12
Sample13
Sample17
Sample18
Sample20
Sample14
Figure 10: Examples of sketched figures used in the tests
including lines (in red) and arcs (in blue).
The segmentation process has been carried out
with a different set of segmentation parameters for
each SA iteration. And the SA process has been
made up with different ranges for segmentation
parameters and different values for SA parameters as
described in section 3.
5 CONCLUSIONS
From results obtained, we can state that the
optimization process improves significantly the
AUTOMATED TUNING OF PARAMETERS FOR THE SEGMENTATION OF FREEHAND SKETCHES
327

results of the segmentation, demonstrating that, in
general, the recognition process can benefit much if
optimization techniques are applied to its parameters
tuning them for their optimal values. The results
improved in more than 10% respect those obtained
with previous parameters fixed empirically from
observation. The segmentation approach SegSGeo
with the optimization process obtained a success of a
92% of well segmented figures (all-or-nothing-
accuracy), which increases to 97% if we consider
isolated entities instead of complete figures.
With respect to the optimization technique, tests
with different SA parameters show a very stable
behavior of SA algorithm, so it can find good
solutions though the SA parameters vary within a
fairly wide range. The most critical parameter is the
displacement mechanism, that is, the maximum
displacement ratio α: it must be high enough to get
out from local minimum, but not too high to avoid
jumping haphazardly (see figure 11).
0
10
20
30
40
50
60
70
80
90
100
0 100 200 300
0
10
20
30
40
50
60
70
80
90
100
0 100 200 300 400 500
Figure 11: Cost evolution in two different SA processes
(above: α=0.4) (below: α=0.1).
The following parameters in order of importance
are those that control the cooling scheme: the initial
temperature T
0
and cooling coefficient k. The
probability of finding an optimal solution increases
when more tests are performed with a slow cooling
(higher T
0
, or k closest to 1), but increasing the time
too. Good solutions can be found with a set of SA
process with a fast cooling scheme or with a single
SA process with a slow cooling scheme.
Tests show that classical values for balance and
freezing criterions (dependent on the number of
parameters to optimize) are appropriate. On the one
hand, changes in balance criterion have a similar
effect that changes in cooling scheme, on the other
hand, changes on freezing criterion do not
significantly affect the SA time or result.
REFERENCES
Azar, S., Couvreury, L., Delfosse, V., Jaspartz, B. and
Boulanger, C. (2006). An agent-based multimodal
interface for sketch interpretation. In Proceedings of
International Workshop on Multimedia Signal
Processing (MMSP-06), 488 - 492.
Casella, G., Deufemia, V., Mascardi, V., Costagliola, G.
and Martelli, M. (2008). An agent-based framework
for sketched symbol interpretation. Journal of Visual
Languages and Computing, 19, 225–257.
Davis, R. C., Colwell, B. and Landay, J. A. (2008). K-
Sketch: A ‘Kinetic’ Sketch Pad for Novice Animators.
Proceedings of the twenty-sixth annual SIGCHI
conference on Human factors in computing systems.
Aesthetics, Awareness, and Sketching, 413-422.
Fernández-Pacheco, D. G., Aleixos, N., Conesa, J. and
Contero, M. (2009). Natural interface for sketch
recognition. Advances in Intelligent and Soft
Computing, 55, 510-519.
Fernández-Pacheco, D. G., Conesa, J., Aleixos, N.,
Company, P. and Contero, M. (2009). An agent-based
paradigm for free-hand sketch recognition. Lecture
Notes in Artificial Intelligence, 5883, 345-354.
Flasinski, M., Jurek, J. and Myslinski, S. (2009). Multi-
agent System for Recognition of Hand Postures.
Lecture Notes in Computer Science, 5545, 815-824.
Gelasca, E. D., Salvador, E. and Ebrahimi, T. (2003).
Intuitive strategy for parameter setting in video
segmentation. Visual communications and image
processing, SPIE proceedings series, 5150 (3), 998-
1008.
Iakovidis, D. K., Savelonas, M. A., Karkanis, S. A. and
Maroulis, D. E. (2007). A genetically optimized level
set approach to segmentation of thyroid ultrasound
images. Applied Intelligence, 27 (3), 193-203.
Juchmes, R., Leclercq P. and Azar, S. (2005). A freehand-
sketch environment for architectural design supported
by a multi-agent system. Computers & Graphics, 29
(6), 905–915.
Kirkpatrick, S., Gelatt, C. D. and Vecchi, M. P. (1983).
Optimization by Simulated Annealing. Science, 220
(4598), 671-680.
Kouvelis, P. and Chiang, W. C. (1992). A simulated
annealing procedure for single row layout problems in
Cost
Iterations
Cost
Iterations
GRAPP 2011 - International Conference on Computer Graphics Theory and Applications
328

flexible manufacturing systems, International Journal
of Production Research, 30 (4), 717-732.
Mbogho, A. J. & Scarlatos, L. L. (2007). Genetic
parameter tuning for reliable segmentation of colored
visual tags. In Proceedings of the 9th Annual
Conference on Genetic and Evolutionary
Computation, ACM, 1525-1525.
Mukerjee, A., Agrawal, R. B., Tiwari, N. and Hasan, N.
(1997). Qualitative sketch optimization. Artificial
intelligence for engineering design, analysis and
manufacturing, 11 (4), 311-323.
Taylor, G. W. & Wolf, C. (2004). Reinforcement Learning
for Parameter Control of Text Detection in Images and
Video Sequences. In Proc. of the IEEE International
Conference on Information & Communication
Technologies.
Varley, P. & Company, P. (2008). Automated sketching
and engineering culture. In Proceedings of VL/HCC
Workshop Sketch Tools for Diagramming, 83-92.
Yu, B. (2003). Recognition of freehand sketches using
mean shift. In Proceedings of IUI, 204–210.
AUTOMATED TUNING OF PARAMETERS FOR THE SEGMENTATION OF FREEHAND SKETCHES
329
