
EVALUATION OF FEATURES AND COMBINATION APPROACHES
FOR THE CLASSIFICATION OF EMOTIONAL SEMANTICS IN
IMAGES
Ningning Liu, Emmanuel Dellandr
´
ea, Liming Chen
Universit
´
e de Lyon, CNRS
Ecole Centrale de Lyon, LIRIS, UMR5205, F-69134, Lyon, France
Bruno Tellez
Universit
´
e de Lyon, CNRS
Universit
´
e Lyon 1, LIRIS, UMR5205, F-69622, Lyon, France
Keywords:
Emotional semantic, Image classification, Evidence theory.
Abstract:
Recognition of emotional semantics in images is a new and very challenging research direction that gains
more and more attention in the research community. As an emerging topic, publications remains relatively
rare and numerous issues need to be addressed. In this paper, we propose to investigate the efficiency of
different types of features including low-level features and proposed semantic features for classification of
emotional semantics in images. Moreover, we propose a new approach that combines different classifiers
based on Dempster-Shafer’s theory of evidence, which has the ability to handle ambiguous and uncertain
knowledge such as the properties of emotions. Experiments driven on the International Affective Picture
System (IAPS) image databases, which is a common stimulus set frequently used in emotion psychology
research, demonstrated that the proposed approach can achieve promising results.
1 INTRODUCTION
In recent years, online photo sharing communities are
emerged and are growing (like, flick.com, photo.net,
dpchallenge.com, deviantart.com). In the era of in-
formation explosion especially with more and more
pictures and other multimedia, it is an urgent thing
to continuously develop intelligent systems for au-
tomatic image emotional semantic analysis.(A. W.
M Smeulders, 2000; R. Datta, 2005)
One of the goals of computer science, and partic-
ularly artificial intelligence is to elaborate intelligent
computers having the ability to interact with human
beings in a natural way. Thus, one of key issues is
to allow computers to recognize, understand and ex-
press emotions, and numerous works have been done
for recent years on these aspects (J. Z.Wang, 2001;
K. Kuroda, 2002; Picard, 1997; C. Columbo, 1999;
C.-H. Chan, 2005; S. Wang, 2005; C.-T. Li, 2007;
Z. Zeng, 2009; W. Wang, 2008).
As far as emotion recognition is concerned, re-
searches mainly focus on affect recognition in audio
(speech and music) and visual based facial expres-
sions. Limited contributions deal with the recogni-
tion of emotions carried by images (V.Yanulevskaya,
2008; W. Wei-ning, 2006; S. Wang, 2005; Q. Wu,
2005; C. Columbo, 1999), and a lot of issues need
to be addressed particularly concerning the three fol-
lowing fundamental problems: emotion models, fea-
ture extraction for emotion recognition and classifi-
cation schemes to handle the distinctive characteris-
tics of emotions, and the main difficulty remains to
bridge the gap between low-level features extracted
from images and high level semantic concepts such
as emotions.
Several models have been considered in the litera-
ture to represent emotions (P. Dunker, 2009), and the
two main approaches are the discrete one and the di-
mensional one. The first model consists in consider-
ing adjectives or nouns to specify the emotions, such
as happiness, sadness, fear, anger, disgust and sur-
prise. The second model describes emotions accord-
352
Liu N., Dellandréa E., Chen L. and Tellez B..
EVALUATION OF FEATURES AND COMBINATION APPROACHES FOR THE CLASSIFICATION OF EMOTIONAL SEMANTICS IN IMAGES.
DOI: 10.5220/0003364603520357
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 352-357
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ing to one or more dimensions representing a special
mood characteristic, such as pleasure, arousal or con-
trol. These models allow representing a wider range
of emotions than the first one. In this paper, the di-
mensional model has been employed as illustrated in
Fig. 1.
Few works have been done to propose an efficient
automatic images emotion recognition system. Yan-
ulevskaya et al. (V.Yanulevskaya, 2008) propose an
emotion categorization approach for art works based
on the assessment of local image statistics using sup-
port vector machines. Wang et al. (S. Wang, 2005)
uses a Support Vector Machine of Regression to pre-
dict values of emotional factors based on three im-
age features: luminance fuzzy histogram, saturation
fuzzy histogram integrated with color contrast and
luminance contrast integrated with edge sharpness.
Colombo et al. (C. Columbo, 1999) use a suitable
set of rules to extract some intermediate semantic lev-
els, and then build the semantic representation by
a process of syntactic construction called composi-
tional semantics. Wu et al. (Q. Wu, 2005) use SVMs
to learn the mapping correlation between affective
space and visual feature space of images, and then the
trained SVMs are used to estimate and classify im-
ages automatically. However, no study has attempted
to identify the most adapted features and type of clas-
sifiers to handle the characteristics of emotions which
are high-level semantic concepts. Thus, we propose
in this paper to evaluate the efficiency of different
types of features and combination methods for emo-
tion recognition. Moreover, we present a novel com-
bination approach based on Dempster-Shafer’s The-
ory of Evidence, which allows to handle ambiguity
and uncertainty which are characteristics of emotions.
The rest of this paper is organized as follows. Im-
age features used for characterizing emotions in im-
ages are presented in section 2. The proposed fusion
of information based on the Theory of Evidence is de-
tailed in section 3. Experiments setup and results are
presented in section 4, followed by the conclusion in
section 5.
2 IMAGE FEATURES FOR
EMOTION CLASSIFICATION
2.1 Low-level Image Features
Most of works dealing with emotion recognition
make use of traditional image features that are also
used for other computer vision problems. The three
main categories of image features are based on color,
texture and shape informations. Concerning color,
studies have shown that HSV (Hue, Saturation, Value)
color space is more related to human color percep-
tion than others such as RGB color space. Based on
HSV color space, authors (P. Dunker, 2009; Q. Wu,
2005) use several ways to describe color contents in
images such as moments of color, color histograms,
correlograms and histograms of color temperature.
Concerning texture, Tamura features (Q. Wu, 2005)
have been proven to correlate strongly with human
visual perception: coarseness, contrast, directionality.
The spatial grey-level difference statistics (C.-T. Li,
2007), known as co- occurrence matrix, can describe
the brightness relationship of pixels within neighbour-
hoods, and the local binary pattern (LBP) descriptor
is a powerful feature for image texture classification.
Figure 1: A dimensional emotion model: dimension of
pleasure (ranging from pleasant to unpleasant) and arousal
(ranging from calm to excited). Each point represents an
image from database IAPS (P. J. Lang, 1999).
Concerning shape, studies on artistic paintings
have brought to the fore semantic meanings of shape
and lines, and it is believed that shapes in a picture
also influence the degree of aesthetic beauty perceived
by humans (Q. Wu, 2005). In this paper, the hough
transform is employed to build a histogram of line ori-
entations in 12 different orientations.
EVALUATION OF FEATURES AND COMBINATION APPROACHES FOR THE CLASSIFICATION OF
EMOTIONAL SEMANTICS IN IMAGES
353

2.2 Semantic Image Features
Some attempts have been made to identify higher
level image features linked to emotions. Thus, studies
on artistic paintings have brought to the fore seman-
tic meanings of color and lines that have been used
for designing image features for emotion recognition
purposes in the work of (C. Columbo, 1999). Indeed,
Figure 2: Itten’s chromatic circle.
color combinations can produce effects such as har-
mony, non-harmony, calmness and excitation. The vi-
sual harmony can be obtained by combining hues and
saturations so that an effect of stability on human eye
can be produced. This harmony can be represented
thanks to Itten’s chromatic circle (Itten, 1961) where
colors are organized into a chromatic circle and con-
trasting colors have opposite coordinates according to
the center of the circle (Fig. 2). To extract an im-
age feature that characterizes harmony, dominant col-
ors in the image are first identified and plotted into
the chromatic circle. Then, the polygon linking these
colors is considered. The harmony can finally be de-
scribed by a value in such a way that a value next to 1
corresponds to a regular polygon whose center is next
to the circle center which characterizes a harmonious
image, and a value next to 0 corresponds to an irregu-
lar polygon characterizing a non harmonious image.
Lines also carry important semantic information
in images: oblique lines communicate dynamism and
action whereas horizontal or vertical lines rather com-
municate calmness and relaxation. To characterize
dynamism and action in images, the ratio is computed
between the numbers of oblique lines respect to the
total number of lines in an image.
3 THE THEORY OF EVIDENCE
FOR EMOTION RECOGNITION
Emotions are high-level semantic concepts that are by
nature highly subjective and ambiguous. Thus, in or-
der to perform efficiently this recognition task, it is
necessary to handle informations that can be uncer-
tain, incomplete, ambiguous and leading to conflicts,
this paper attempts to solve this issue by proposing a
new technique based on the Theory of Evidence.
3.1 Fundamentals of the Theory of
Evidence
The Theory of Evidence (Dempster, 1968) introduced
by Dempster and then formalized by Shafer (Shafer,
1976) and Smets(Smets, 1990) offers a theory allow-
ing the reasoning on knowledge that can be uncertain,
incomplete, and leading to conflicts.
Let Ω = {H
1
, H
2
, . . . , H
n
} be a finite set of possi-
ble hypotheses. This set is referred to as the frame of
discernment, and its power set denoted by 2
Ω
. Fol-
lowing are the basic concepts of the theory:
Belief Mass Functions. The confidence, or belief, we
can have in a hypothesis given a source of information
(a type of feature in our case) is expressed by the mass
function m associated to this source of information.
Thus, the mass function assigns a value in [0, 1] to
every subset A of Ω and satisfies the following:
m
Ω
(
/
0) = 0 and
∑
A⊆Ω
m
Ω
(A) = 1 (1)
Combination Rule. Different mass functions from
several sources of information can be combined to im-
prove the knowledge used for the classification deci-
sion. Let m
Ω
S1
and m
Ω
S1
be two mass functions from
two independent sources of information S1 and S2.
Then, the Transferable Belief Model (TBM) (Smets,
1990) combined mass function m
Ω
S1∩S2
of an hypothe-
sis A ⊆ Ω is given by:
m
Ω
S1⊕S2
(A) =
∑
B∩C=A
m
Ω
S1
(B).m
Ω
S2
(C)
1 − m
Ω
S1⊕S2
(
/
0)
(2)
where m
Ω
S1⊕S2
(
/
0) =
∑
B∩C=
/
0
m
Ω
S1
(B).m
Ω
S2
(C)
3.2 Computation of the Evidence
We propose in this paper an original approach for
computing evidence. The principle is as follows. For
each type of feature, considered as source of informa-
tion S
j
, SVM classifiers are first trained to recognize
each of the classes, or hypotheses H
i
. The outputs
of these classifiers are used to compute the beliefs.
This is done by applying on them membership func-
tions, represented in Fig. 3 allowing to give a belief to
the different classes and combination of classes, ac-
cording to classifiers. However, the classifiers are not
perfect and can be mistaken. To integrate this, the
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
354
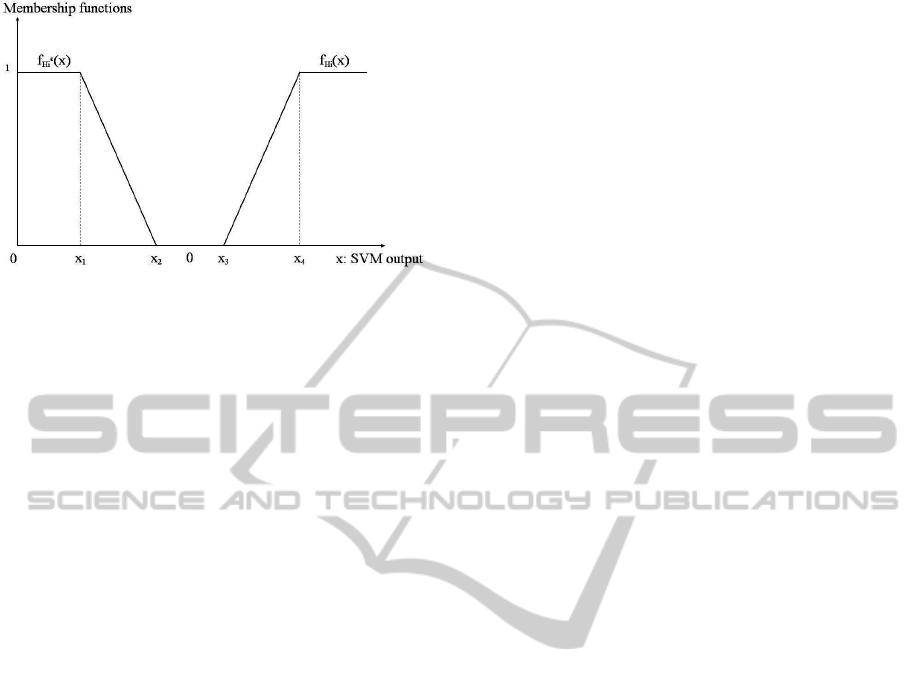
Figure 3: Membership functions f
H
i
and f
H
c
i
, associated re-
spectively to classes H
i
and H
c
i
, applied on SVM output x
to build mass functions.
efficiency of the classifiers (i.e. precision, given by
the confusion matrix) is used to weight their decision.
This is formalized as follows.
Let S
1
, S
j
, S
m
be the m sets of features considered
as sources of information. For all S
j
, n binary clas-
sifiers c
i j
are trained to recognize the n classes H
i
.
Let now consider the building of the mass function
m
c
i j
corresponding to the belief mass obtained from
source of information S
j
using classifier c
i j
trained to
recognize class H
i
. According to the output x
i j
of c
i j
,
and using membership functions (Fig. 3), the mass is
distributed on three subsets of Ω: Ω itself, H
i
and H
c
i
the complement of H
i
in Ω as in Eq. 5.
m
c
i j
(H
i
) = f
H
i
(x). p
c
i j
(H
i
) (3)
m
c
i j
(H
c
i
) = f
H
c
i
(x). p
c
i j
(H
c
i
) (4)
m
c
i j
(Ω) = 1 − m
c
i j
(H
i
) − m
c
i j
(H
c
i
) (5)
where p
c
i j
(H
i
) is the precision of c
i j
for class H
i
and p
c
i j
(H
c
i
) is the precision of c
i j
for class H
c
i
, both
computed from the confusion matrix of c
i j
.
Thus, if the output x of classifier c
i j
is a high pos-
itive value, it means that c
i j
is sure that the input is
in class H
i
. But, as c
i j
may be mistaken, the mass is
distributed not only on H
i
but also on Ω which corre-
sponds to uncertainty, according to the ability of c
i j
to correctly recognize H
i
. On the contrary, if x is very
negative, it means that c
i j
is sure that the input is in
class H
c
i
. However, this decision is also weighted by
the ability of c
i j
to correctly recognize H
c
i
, leading to
a distribution of mass between H
c
i
and Ω. Finally, if
x is around 0, it means that classifier c
i j
has a doubt,
thus the mass is in majority given to Ω, which corre-
sponds to uncertainty.
Once mass functions m
c
i j
are computed from all
classifiers c
i j
, they are combined according to a given
combination operator, such as Dempster’s one (Eq.2),
which corresponds to a fusion of informations given
by all sources S
j
. Finally, a single mass function is
obtained distributing the belief over some subsets of
Ω. The final decision can be taken according to deci-
sion measures presented in section 3.1.
4 EXPERIMENTS
In our experiments, we have made used of the IAPS
database (P. J. Lang, 1999), which provides ratings of
affect (pleasure or valence, arousal and control) for
1192 emotionally-evocative images. We have con-
sidered an emotion model based on the pleasure and
arousal dimensions using four classes corresponding
to each quadrant as shown in Fig. 5. The IAPS cor-
pus is partitioned into a train set (80% of the data, 953
images) and a test set (20% of the data, 239 images),
and all the experiments repeated ten times to get the
average correct classification rate (CR).
To explore the performance of different feature
sets for visual emotion recognition presented in Sec-
tion 2, we have built a classification scheme using two
support vector machine classifiers to identify each
class: the first one is to identify arousal dimension,
and the second one is dedicated to the pleasure di-
mension. The results obtained are shown in Figure 6.
From these results, it appears that among the dif-
ferent features, texture (LBP, Tamura) are the most ef-
ficient ones. Moreover, the higher level features (dy-
namism and harmony) may first seem giving lower
performance, but as they consist in a single value,
their efficiency is in fact remarkable.
To evaluate the efficiency of different types of
combination approaches, we have built an emotion
classification scheme that combined classifiers based
on different features according to the framework il-
lustrated in Fig. 4. In these systems, SVM classifiers
are employed and each feature set S
j
was used to train
classifiers c
i j
, which produces measurement vector y
i j
corresponding to the probability of inputs to belong
to different classes C
i
. Vectors y
i j
are then used to
perform the combination to get the classification re-
sults according to section 3.2. The following com-
bination methods have been implemented and com-
pared to our approach based on the Theory of Evi-
dence: maximum-score, minimum-score, mean-score
and majority-score. The results obtained are shown in
Table 1.
These results show that fusion with the Theory of
Evidence is more efficient with an average percent-
age of 54.7% compared to fusion with mean-score,
min-score, max-score, and majority voting, according
to following equation (Robert Snelick, 2005) , which
proves the ability of the Theory of Evidence to com-
EVALUATION OF FEATURES AND COMBINATION APPROACHES FOR THE CLASSIFICATION OF
EMOTIONAL SEMANTICS IN IMAGES
355

Figure 4: The classification scheme, which combined different classifier outputs.
Table 1: The accuracy for four classes, performed by the different fusion methods.
Max
score
Min
score
Mean
score
Majority
voting
Proposed
combined
I 56.32 51.25 50.87 55.20 58.97
II 53.08 50.24 52.51 53.36 55.00
III 52.67 48.31 50.43 47.37 51.76
IV 50.34 51.42 53.67 52.30 53.08
CR 51.87 50.31 53.10 52.05 54.70
Figure 5: The dimensional emotion model is used to define
4 classes of emotions corresponding to the 4 quadrants.
bine the different sources of information and to ex-
ploit their complementarities.
Z(i) =
1
N
N
∑
n=1
y
n
i
.∀i. (6)
Z(i) = min(y
1
i
, y
2
i
, ..., y
N
i
), ∀i. (7)
Z(i) = max(y
1
i
, y
2
i
, ..., y
N
i
), ∀i. (8)
Z(i) = argmax(y
1
i
, y
2
i
, ..., y
N
i
), ∀i. (9)
where y
n
i
represent the i
th
measurement of classifier
C
n
.
Figure 6: The average correct classification rate obtained
using individual feature set.
5 CONCLUSIONS
We have investigated in this work the efficiency of
different types of features and combination of clas-
sifiers for visual emotion recognition in realistic im-
ages. Experiments on IAPS dataset have brought
to the fore that texture features as well as harmony
and dynamism features carry important information
for the emotional semantics classification purpose.
Moreover, the proposed fusion approach based on
the Theory of Evidence has achieved an encouraging
classification rate, certainly due to its ability to repre-
sent uncertainty and ambiguity of emotions.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
356

ACKNOWLEDGEMENTS
This work is partly supported by the French ANR un-
der the project Omnia ANR-07-MDCO-009.
REFERENCES
A. W. M Smeulders, Marcel Worring, S. S. A. G. R. J.
(2000). Content-based image retrieval: the end of the
early years. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 22(12):1349–1380.
C. Columbo, A. Del Bimbo, P. P. (1999). Semantics in vi-
sual information retrieval. IEEE Multimedia, 6(3):38–
53.
C.-H. Chan, G.-J.-F. J. (2005). Affect-based indexing and
retrieval of films. ACM Multimedia, pages 427–430.
C.-T. Li, M.-K. S. (2007). Emotion-based impression-
ism slideshow with automatic music accompaniment.
ACM Multimedia, pages 839–842.
Dempster, A. P. (1968). A generalization of bayesian infer-
ence. Journal of the Royal Statistical Society, Series
B, 30:205–247.
Itten, J. (1961). The art of color. Otto Maier Verlab, Ravens-
burg, Germany.
J. Z.Wang, J. L. (2001). Simplicity: Semantics-sensitive
integrated matching for picture libraries. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
23(9):947C963.
K. Kuroda, M. H. (2002). An image retrieval system by
impression words and specific object names iris. euro
computing, 43:259–276.
P. Dunker, S. Nowak, A. B. C. L. (2009). Content-based
mood classification for photos and music. ACM MIR,
pages 97–104.
P. J. Lang, M. M. Bradley, B. N. C. (1999). The iaps: Tech-
nical manual and affective ratings. Tech. Rep. GCR in
Psychophysiology.
Picard, R. W. (1997). Affective computing. MIT Press,
Cambridge.
Q. Wu, C. Zhou, C. W. (2005). Content-based affective
image classification and retrieval using support vector
machines. ACII, pages 239–257.
R. Datta, J. Li, J. Z. W. (2005). Content-based image re-
trieval: approaches and trends of the new age. ACM
Workshop MIR, Singapore, pages Nov. 11–12.
Robert Snelick, Umut Uludag, A. M. M. I. A. J. (2005).
A survey of affect recognition methods: audio, vi-
sual and spontaneous expressions. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
27(3):450–455.
S. Wang, X. W. (2005). Emotion semantics image retrieval:
a brief overview. ACII, pages 490–497.
Shafer, G. (1976). A mathematical theory of evidence.
Princeton University Press.
Smets, P. (1990). The combination of evidence in the trans-
ferable belief model. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 12(5):447–458.
V.Yanulevskaya, J.C.Van Gemert, e. a. (2008). Emotional
valence categorization using holistic image features.
ICIP, pages 101–104.
W. Wang, Q. H. (2008). A survey on emotional semantic
image retrieval. ICIP, pages 117–120.
W. Wei-ning, Y. Ying-lin, J. S.-m. (2006). Image retrieval
by emotional semantics: A study of emotional space
and feature extraction. IEEE ICSMC, 4.
Z. Zeng, M. Pantic, G. I. R. T. S. H. (2009). A survey of
affect recognition methods: audio, visual and spon-
taneous expressions. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 31(1):39–58.
EVALUATION OF FEATURES AND COMBINATION APPROACHES FOR THE CLASSIFICATION OF
EMOTIONAL SEMANTICS IN IMAGES
357
