DATA RELIABILITY AND DATA SELECTION

IN REAL TIME HIGH FIDELITY SENSOR NETWORKS

Nina Peterson

Department of Natural Sciences and Mathematics, Lewis-Clark State College, Lewiston, Idaho, U.S.A.

Behrooz A. Shirazi, Medha Bhadkamkar

School of Electrical Engineering and Computer Science, Washington State University, Pullman, Washington, U.S.A.

Keywords: Data quality, Data selection, Wireless sensor networks, Bayesian network, Knapsack optimization.

Abstract: Due to advances in technology, sensors in resource constrained wireless sensor networks are now capable of

continuously monitoring and collecting high fidelity data. However, all the data cannot be trusted since data

can be corrupted due to several reasons such as unreliable, faulty wireless sensors or harsh ambient

conditions. Further, due to bandwidth constraints that limit the amount of data being transmitted in sensor

networks, it is important that only the high priority, accurate data is transmitted. In this paper, we propose a

data selection model that makes two significant contributions. First, it provides a way to determine the

confidence in or reliability of the data values and second, it determines which subset of data is of the highest

quality or of most interest given the state of the network system and its current available bandwidth. Our

model is comprised of two phases. In Phase I we determine the reliability of each input data stream using a

Bayesian network. In Phase II, we use a 0-1 Knapsack optimization approach to choose the optimal subset

of data. An evaluation of our best data selection model reveals that it eliminates erroneous data and

accurately determines the subset of data with the highest quality when compared with conventional

algorithms.

1 INTRODUCTION

There is an increasing demand for high fidelity,

continuous data sampling from resource constrained

wireless sensor network environments. For instance,

real-time applications that monitor environments,

such as an active volcano, employ wireless sensor

networks to continuously monitor, collect and

analyze data under extreme environmental

conditions such as snow, wind, rain or ice. Ideally,

we should be able to collect and transmit all this data

continuously. However, in the real world, this is not

feasible since the continuously sampled data is of

such high frequency and resolution that it can

quickly consume all the available bandwidth and

drop data packets during transmission. Additionally,

due to sensor malfunctions and harsh environmental

conditions, the quality of data cannot be trusted at all

times. Thus, it is imperative that only the high

quality data is transmitted over the network, and the

remaining data is transmitted only if bandwidth

space permits. The quality of data for any wireless

sensor network deployment is an important issue

that has ramifications in network management and is

of significance to the user. Dynamic scheduling

algorithms, such as Tiny-DWFQ (Peterson et al.,

2008), are complementary to this work and may be

utilized to assign priorities to the data to ensure that

high quality data would be made available to the end

users.

This paper presents a two-phase, best data

selection model that determines the best subset of

data to select from a given set of input data streams

in a sensor network. Phase I identifies reliable data

from different input data streams, while Phase II

selects the best data subset for delivery to the end

user given the network bandwidth. We applied our

model to the data collected by a volcanic monitoring

sensor network (called OASIS) deployed at Mount

St. Helens, an active volcano site. The sensors in

OASIS collect and transmit hi-fidelity data in real

time which may be prone to errors and hence

Peterson N., A. Shirazi B. and Bhadkamkar M. (2011).

DATA RELIABILITY AND DATA SELECTION IN REAL TIME HIGH FIDELITY SENSOR NETWORKS .

In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems, pages 42-53

DOI: 10.5220/0003365600420053

 SciTePress

provides an ideal framework for the evaluation for

our model. Our results reveal that our model

determines the most appropriate subset of data with

high accuracy.

The rest of the paper is organized as follows.

Section 2 discusses the motivations for and

contributions of the project. To elucidate our setup,

we present relevant background information in

Section 3. Details of each phase of our model

including our solutions to relevant challenging

issues they posed are discussed in Section 4. We

present our analysis and evaluation of the proposed

system in Section 5 and make concluding remarks in

Section 6.

2 MOTIVATIONS

AND CONTRIBUTIONS

Our motivation for developing the optimal data

selection model was due to the lack of an acceptable

existing solution. Our investigation revealed that

amongst the researchers who addressed optimal data

selection, there were three common shortcomings

that degraded the overall performance of the system.

In this section, we discuss each of these

shortcomings and how we address them in our

optimal data selection model. Our solution enables

us to achieve an overall enhanced accuracy.

2.1 Improving Data Confidence

and Assignment

The first issue we observed in the existing solutions

was the method in which the data confidence levels

(reliabilities) were assigned. We define the data

confidence level as the assurance or belief that the

data value we obtained is correct when compared to

the true value. It is a measure of the reliability of the

data and is a crucial parameter in several studies.

In previous work for optimal data selection in

wireless sensor networks, the user assigned a

confidence level to each type of data or each

individual parameter using either expert knowledge

(Lee and Meier, 2007) (Kumar, et al., 2003) or a

very simplistic metric such as ranking or thresholds

(Ahmen et al., 2005) (Bettini et al., 2007). While

both expert knowledge and user-defined threshold

values have an impact on the confidence level of the

data, we believe that these methods are only reliable

in extremely simplistic situations and environments.

For example, if the threshold method was used to

determine the “hotness” inside a building, a

threshold of 75°F would be reasonable, given the

criteria. However, in several sophisticated scenarios,

such as our volcanic activity monitoring scenario,

numerous factors and complex conditions affect the

data values continuously and using non-adaptive

threshold values to assign data confidence levels can

produce inaccurate results. Hence, we developed an

adaptive optimized confidence level mechanism

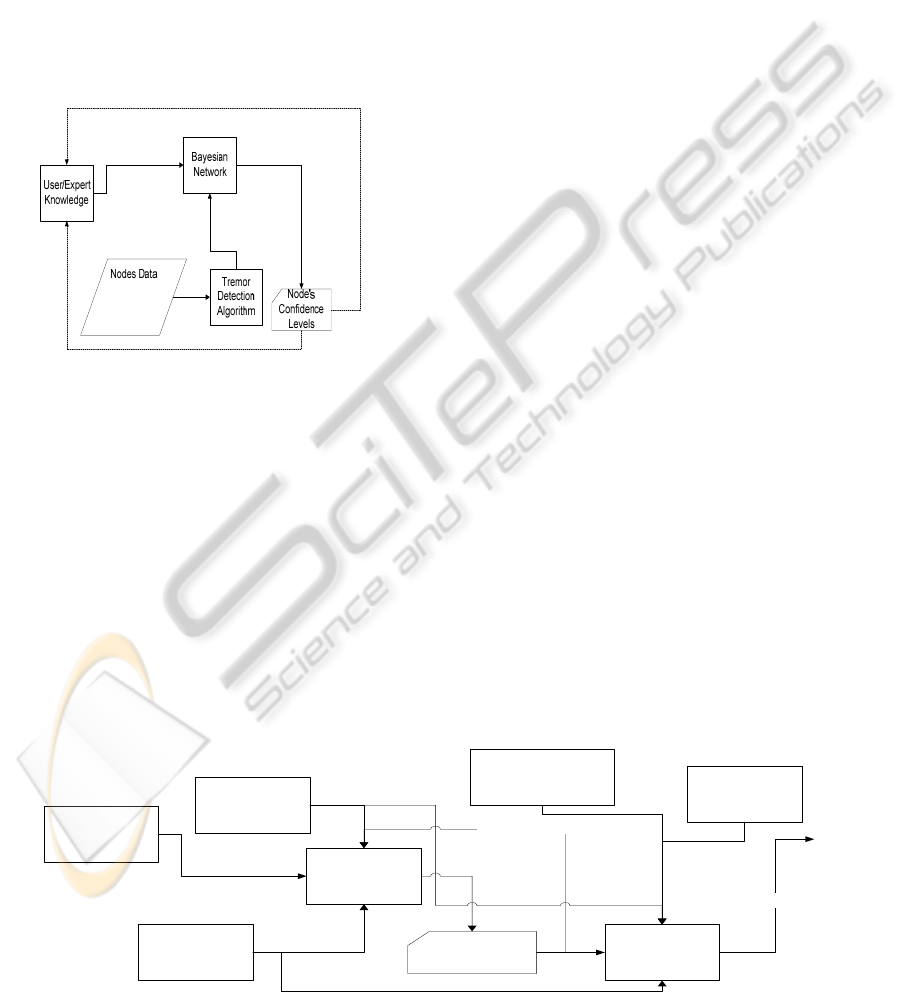
using a Bayesian Network as shown in Figure 1. The

Bayesian Network minimizes the effects of users’

(expert) knowledge imperfections and allows us to

render a dynamic confidence level to each data flow.

Our Bayesian network uses both expert knowledge

and node data as the input parameters. Using this

input, the Bayesian network is able to determine the

confidence level of the node’s data. This is further

discussed in detail in Section IV. Before passing the

raw data into the Bayesian network we first run it

through a tremor detection algorithm. The tremor

detection algorithm is the industry standard that is

used for determining the possibility of seismic

activity.

2.2 Dynamic Confidence Assignments

Existing confidence value assignments mechanisms

are generally static and do not change through the

lifetime of the network (Bettini et al., 2009). We

believe that it is unrealistic to assume that the

reliability of sensors and their readings do not

change (possibly drastically) throughout the lifetime

of the network. For example, let us assume that

shortly after deployment, node X recorded accurate

seismic data and was assigned a corresponding

confidence level of 98%. However, a minor eruption

(or rock fall) caused severe damage to the antenna

for node X, resulting in bad readings. In this

scenario, it would be damaging to the network to

continue to represent node X’s seismic reading with

a confidence level of 98%.

To adapt to the continually changing state of the

network, we designed our confidence level

assignment to be dynamic, where the Bayesian

network re-computes the confidence level for each

data stream after a certain, application specific, time

period (say every 5 minutes). The user can also

execute a re-computation if necessary.

The dynamic confidence assignment also reduces

the impact of any errors that result from the user’s

input to the system. While we do not believe that the

user knowledge or a threshold should be the sole

criteria for determining the confidence level, to

some degree this information must be inserted into

the model. Thus, we use this information as a

DATA RELIABILITY AND DATA SELECTION IN REAL TIME HIGH FIDELITY SENSOR NETWORKS

starting point and continually update and adjust the

confidence level to minimize any errors in these

values. The Bayesian Network allows us to render a

dynamic confidence level to each data flow. We

choose to use a Bayesian network for two reasons.

First, it has an inherent ability to minimize

inaccuracies within the system. For example, if one

of the parameters, say y has an initial probability of

q, any errors in the assignment of q are minimized

by the other variables and their relationships within

the network. This property of Bayesian networks can

be seen in the ability of the user to assign equal,

random or normalized probabilities to variables to

which an initial probability is unknown.

Figure 1: Adaptive Optimized Confidence Level.

Secondly, Bayesian networks do not require all

the possible outcomes to be expressed. In order to

express all outcomes, extensive knowledge of all

possible actions that may occur must be known. This

is fine for a very controlled and simplistic scenario;

however our real world volcanic scenario makes this

assumption impractical, if not impossible.

2.3 Optimal Subset Selection

In our investigation of the current context modelling

techniques developed for wireless sensor networks,

it appears that none of them address the optimal

subset selection problem. Optimal subset selection

has been studied and proven to be beneficial in many

other areas of research since it allows one to inject

the best possible subset of data in the network to

maximize one’s return.

In order to choose the optimal subset of data, we

utilized a 0-1 Knapsack approach. This enabled us to

maximize the return (in our case value or priority of

the data) while minimizing the cost (in our case cost

of transmission in terms of bandwidth). This ensures

that data with a low confidence (say 5%) does not

degrade the network performance as it could in the

general models. It should be noted that cluster data

is used as an input to the Bayesian network, as

shown in Figure 2, in order to both provide a way to

validate the data of closely placed nodes

(geographically) and to be able to provide a way to

identify areas of activity. A cluster is a group of

neighboring sensor nodes whose data are correlated

to determine the occurrence of an event (such as a

tremor in the context of volcano monitoring).

The quality of the data which is the output of

Phase I, the current data priority and the network

bandwidth are input to Phase II. The current data

priority is an adaptive measure of the importance of

a specific data type. Like the seismic data reliability,

the seismic data priority is also derived from Phase

I. The Bayesian network does not directly determine

the occurrence of a tremor. However, the occurrence

of a tremor directly affects the rest of the network

that it was a part of. We choose to utilize this in

order to assign a seismic data priority to each data

flow. This allowed us to give more importance to

nodes in area(s) where we believe activity (seismic

tremor) is occurring. This is very important as we

are not just interested in the most reliable data but

rather in the most important, reliable data. Thus we

combine (through a summation) the seismic data

reliability and the seismic data priority into one

entity, the confidence parameter, vi. This is

discussed in detail in Section 4.

Figure 2: Optimal Data Selection.

U se r/E xp e rt

Input

Bayesian

Network

Q uality of

Data

Updates baseline confidence

Cluster Data

0-1

Knapsack

O p tim a l d a ta su b s e t

Nodes Data

Bandw idth

R esources

C u rre n t D a ta

Priority

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

3 BACKGROUND

INFORMATION

3.1 OASIS

In this section, we provide an overview of the

Optimized Autonomous Space In-Situ Sensor-web

(OASIS) (Song et al., 2008), which provides the

testbed for the design and development of our data

selection model. While volcanic sensor-webs used in

previous studies were deployed only for a few

weeks, OASIS is the first volcanic monitoring

sensor network deployment which has been

deployed for over a year at the volcano site at Mount

St. Helens. The OASIS wireless sensor network is

composed of several Imote2 sensor nodes deployed

on Mount St. Helens. Each node is attached to a

seismic sensor, an infrasonic sensor, and a lightning

sensor. To withstand the harsh weather consisting of

snow, ice, wind and rain, these sensors are housed in

a mechanical structure that resembles a “spider”

which is designed by the earth scientists at the U.S.

Geological Survey (USGS, 2009). Multiple car

batteries provide power to all the components

housed in the “spider”. These sturdy “spiders” can

be lowered at desired locations on the mountain by

helicopters. Once the sensors are placed on the

mountain they are able to self-configure and

autonomously determine both the node bandwidth

and power allocations.

OASIS is the first system of its kind that

integrates both ground components (sensors and

control center) and space components (satellite) and

maintains a continuous feedback loop between them.

The feedback loop enables the network to be

accurate, sensitive and robust. For instance, events

overlooked by sensors in a specific area on the

ground can be detected by the satellite which in turn,

can increase the priority of the corresponding

sensors on the ground. Further, if volcanic activity

occurs on a section of the mountain, it reconfigures

the network and re-tasks the satellite to monitor the

area of interest. The high fidelity data is acquired by

the satellite and sent back to the command and

control center. The ground network ingests the data

and re-organizes as needed.

We used the sensor network in OASIS as the

framework for the design and development of our

optimal data selection component.

3.2 Experimental Setup

Before we discuss our model further it is necessary

to describe the experimental scenario we used so

that we can use it as reference in the remainder of

this work.

Figure 3: Experimental Test bed showing the placement of

nodes on Mt. St. Helens.

Our test-bed scenario originated from the real

sensor node deployment on Mount St. Helens. We

choose to use both real data streams from Mount St.

Helen’s as well as simulated data streams. Due to

lack of recent volcanic activity, we periodically

injected the real data with values to simulate specific

seismic tremor scenarios. The test bed used for all of

our analysis is shown below in Figure 3 in which the

locations of the sensors are marked with a yellow

pin and labeled with a number.

The nodes are grouped into four clusters based

on their geographical location. Cluster 1 contains

four nodes: 9, 11, 12, and 14. Cluster 2 contains

four nodes: 8 13, 15, and 16. Cluster 3 contains five

nodes 1, 2, 3, 10, and 17, and finally, Cluster 4

contains three nodes: 4, 5, and 6.

4 DATA SELECTION MODEL

Our modeling framework is composed of two

phases. Phase I uses an intelligent method for

determining an appropriate confidence parameter for

each data type. In Phase II, we determine the optimal

subset of the data types and the data sources. This

section explains each of these phases in detail.

4.1 Phase I: Bayesian Network

Our goal in Phase I is to determine a confidence

level or reliability for each of the sensor’s data

streams. A data stream is a particular type of data

generated at a particular node. Thus, seismic data

from node X might have a different confidence level

than seismic data from node Y. The reliability of

DATA RELIABILITY AND DATA SELECTION IN REAL TIME HIGH FIDELITY SENSOR NETWORKS

each data stream is determined from the correlation

of each stream and the relationships between nodes

within the same cluster. This information, as well as

expert knowledge, is input into our Bayesian

network as shown in Figure 4.

To determine the reliability, the baseline

reliability needs to be established first. This section

first explains how the baseline reliability is derived

using cross correlations. Next, it explains the

significance of the data from the nodes within a

cluster and how it can be utilized to determine

reliability. It then explains how knowledge from the

experts can be included in our model. Finally, it

discusses the construction of our Bayesian network

using the cross correlations and the expert

knowledge as input.

4.1.1 Baseline Reliability

using Cross Correlation

While it is possible to test the reliability of the

sensors in our lab to determine the baseline

reliability we encounter three major problems with

this approach.

First, it is very difficult to simulate volcanic

activity (or other real-world situations) realistically

in the lab. To accomplish this you need to accurately

vary both the intensity and the frequency of the

volcanic activity in a reasonable manner.

Second, the reliability of a sensor in the field is

drastically different than its reliability in the lab due

to the large amount of variability that is injected into

the situation on the mountain. For example, as the

environment changes, such as when the ash

coverage occurs or a rock falls close to the node

blocking its line of sight to its nearest neighbour, the

baseline reliability of the nodes change accordingly.

However, this degradation cannot be uniformly

applied to the sensors as it depends on its precise

location and its relative positions to the other nodes.

Likewise, our experimentation shows that the lab

can have some negative effects that are not

experienced in the field. For example, within the lab

located on a University campus we noticed extreme

interference in the communication of the nodes from

the high volume of Internet traffic on campus, which

resulted in sub-optimal performance. We did not

experience this same problem in the field as there

was no wireless activity on the volcano apart from

our transmissions.

Thus, we developed a dynamic baseline

reliability framework that uses cross correlation to

determine the reliability of each individual node’s

seismic sensor to detect the occurrence of a tremor.

Our tremor detection algorithm uses an industry

standard cross correlation detection algorithm to

indicate the occurrence of a tremor. For cross

correlation, it is necessary to use the seismic sensor

readings from at least two nearby sensors. Due to the

limited number of sensors deployed in OASIS, we

only considered two sensors at a time when we used

the tremor detection algorithm. In order to use cross

correlation to determine the occurrence of a tremor,

we employed a standard two-party cross.

(1)

Equation 1: Cross Correlation.

Note that x(i) and y(i) are the i

seismic sensor

readings from sensors X and Y, d is the distance

between sensors X and Y, and mx and my are the

mean seismic values for sensors X and Y.

The cross correlation does not provide a

definitive answer to whether a tremor occurred at

sensor X. Instead it indicates the occurrence of a

tremor if the correlation between nodes is high. It is

a common practice to use cross correlation to

determine how well two sensors seismic values

correlate. While not ideal, this is satisfactory

because of the ability of the Bayesian Network to

minimize inaccuracies and it is the most reliable

method currently employed by seismologists.

Additionally, in our real-world deployment this

provided us with a much more accurate

representation than a normal or random distribution

which are both commonly acceptable distributions to

be used as baseline reliabilities with Bayesian

Networks.

Instead of using the cross correlation algorithm

to determine the correlation of individual sensor

nodes as isolated entities (just using two sensors),

we chose to utilize the relationships between the

data collected from a geographically located group

or cluster of nodes. This allows us to take advantage

of these clusters’ relationships in order to gain a

more accurate representation of the network’s

behavior.

4.1.2 Cluster Data

After consulting with domain experts we discovered

that significant seismic activity was not isolated to

one specific sensor but was felt by a group of

neighboring sensors. Thus, if one sensor collected

readings indicative of a tremor but it was not

∑∑

∑

−−−

mydiymxix

))(())((

)))((*))(((

)(

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

detected by any of its neighbor’s sensors then it was

likely erroneous. In order to capture this

characteristic in our model, we chose to implement

our Bayesian network so that it included inter-node

correlations, which is referred to as cluster

correlations and are the correlations between nodes

in a cluster and intra-node correlations, which is

referred to as node correlations and are the

correlations between different data streams of a

node. We utilize this in order to impart additional

knowledge to our model regarding neighboring

cluster nodes.

Because of this and our efforts to incorporate the

entire cluster’s characteristics, we ran the tremor

detection algorithm on every pair of nodes within

each cluster. For example, for Cluster 3, which is

composed of nodes 1, 2, 3, 10, and 17, we had 10

node correlations: {1,2}{1,3}{1,10}{1,17}{2,3}

{2,10}{2,17}{3,10}{3,17} and {10,17}.

Once this was done we needed a way to

consolidate this into one descriptive cross

correlation for each node. Our first thought was to

take the average of the cross correlations for each

node. After further examination, we determined that

this was not a reliable means of describing the cross

correlation of the nodes. Earth Scientists determined

that high threshold of 90% or more corresponds to a

“high correlation”. Thus, if even one node within a

cluster had a low correlation it would bring the

average of the other nodes below the 90% threshold

resulting in an inaccurate description of the other

nodes as having a “low correlation”. Therefore, we

could not use a simple average to determine the

correlation for each node.

Instead, we chose to use a voting scheme. For

each node we determined the number of other nodes

within its cluster with which it had a cross

correlation greater than or equal to 90% and

regarded this as a positive vote. All of the nodes

within the cluster with which the node had a cross

correlation less than 90% were considered a negative

vote. If the number of positive votes was greater

than or equal to the number of negative votes then

the cluster was considered to have a high correlation.

Otherwise, the cluster was assigned a low

correlation. This voting scheme did not allow the

bad data from one node to skew the results from the

rest of the nodes in its cluster.

Next we will discuss the role of the Earth

Scientists’ expert knowledge in our Bayesian

network.

Table 1: Default Probability Cluster Correlations.

Nodes’ correlation

values

Probability of cluster

correlation

High Low

3-node

cluster

All 3 high 100% 0%

All 3 low 0% 100%

2 high and 1 low 70% 30%

1 high and 2 low 10% 90%

4-node

cluster

All 4 high 100% 0%

All 4 low 0% 100%

3 high and 1 low 90% 10%

1 high and 3 low 10% 90%

2 high and 2 low 70% 30%

5-node

cluster

All 5 high 100% 0%

All 5 low 0% 100%

4 high and 1 low 98% 2%

1 high and 4 low 10% 90%

3 high and 2 low 90% 10%

2 high and 3 low 70% 30%

4.1.3 Expert Knowledge

In our optimal data selection model we used expert

knowledge as one input into our Bayesian network.

This was done through the use of a “user’s profile”.

The user profile is created using expert knowledge

and can be modified as necessary.

The purpose of the user profile is to determine

the relationships between every node’s (within the

cluster) seismic sensor correlation values. This

information is input into the Bayesian network in the

form of Conditional Probability Tables (CPT). For

consistency we designed a default user profile for

each cluster scenario as shown below in Tables 1.

Table 1 denotes the default probability cluster

correlation given the nodes’ correlation values for

different cluster sizes (3, 4, and 5 nodes per cluster).

In addition to the CPTs discussed above, expert

knowledge is also used to impart knowledge into

two more CPTs that are used for all networks

regardless of their size. The first one is for the

individual node’s seismic sensor correlation. If a

tremor occurs, the probability of the seismic sensor

correlation is set to 98% (high) and 2% (low),

respectively. Similarly, if a tremor does not occur

the probability of the seismic sensor correlation is

set to 2% (high) and 98% (low), respectively. The

final CPT is for the individual node’s seismic data

reliability. If the node’s seismic correlation and its

cluster correlation agrees (either high or low) then

the reliability is set to 100% (reliable) and 0%

(unreliable), respectively. This means regardless of

what activity is detected, if it is the same then we

deem the node reliable. If the node’s sensor correla-

DATA RELIABILITY AND DATA SELECTION IN REAL TIME HIGH FIDELITY SENSOR NETWORKS

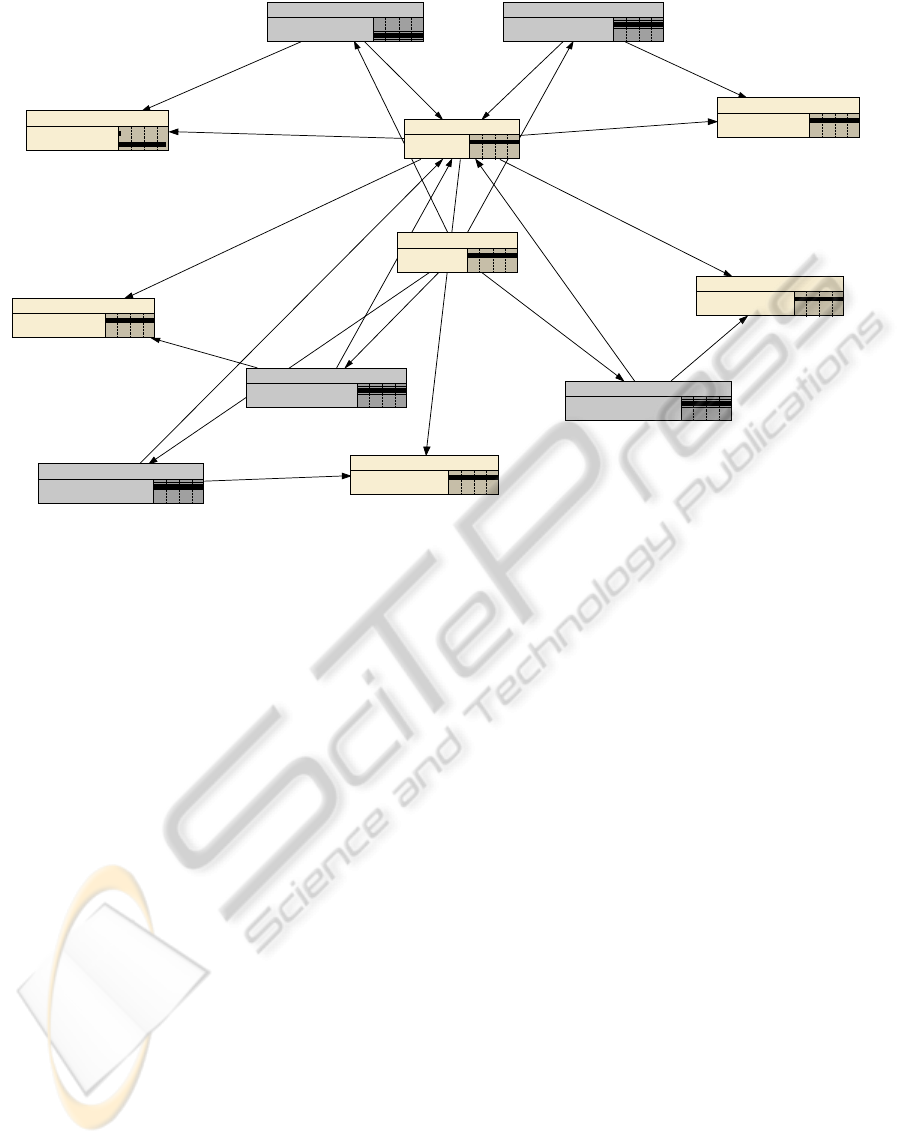
Figure 4: Bayesian Network Example.

tion and the cluster correlation disagree then the

reliability is set to 2% (reliable) and 98%

(unreliable).

4.1.4 Bayesian Network

In our Bayesian network, the existence of a tremor at

a particular cluster is depicted in the center of the

network labeled as ClusterYTremor, where ‘Y’

denotes the node number. Figure 4 shows an

example Bayesian Network for node 3. It should be

noted that in this phase we do not attempt to

determine whether a tremor has occurred. However,

the existence of a tremor is a factor that influences

the seismic sensor correlation and the cluster

correlations which ultimately determine the seismic

reliability of the data. Hence, ClusterYTremor lies at

the center of our network. It should be noted that we

did not need to input whether or not a tremor was

occurring into our Bayesian network as it was not

assumed that this was known. Instead it was

assumed that there was an equal probability of a

tremor occurring or not occurring. Once some

known data, specifically seismic data correlations,

were input into the Bayesian network, it would

automatically adjust the probability of a tremor

occurring. In addition to the ClusterYTremor nodes

in our Bayesian networks, there are other nodes:

NYSeismicSensorCorrelation, where Y is the sensor

N’s node number. Similar to the ClusterYTremor

nodes the value of the ClusterYCorrelation is not

definitively known. However, unlike the

ClusterYTremor node, the probability of the

ClusterYCorrelation is not 50/50. Because we had

additional knowledge about the cluster correlation

we could impart this knowledge into the Bayesian

network in the form a correlation table.

We imparted this knowledge into the table in the

form of probabilities. The final nodes in our

Bayesian networks are labelled

NYSeismicDataReliabiliy, where Y is the nodes

number (N2SeismicDataReliability). This was

represented by a percentage of the confidence that

we had in node Y’s seismic data and it was

computed and returned as the result of executing our

Bayesian network.

Once we determine the data reliability for all the

data streams, we use it as input into Phase II in order

to obtain an optimal data subset.

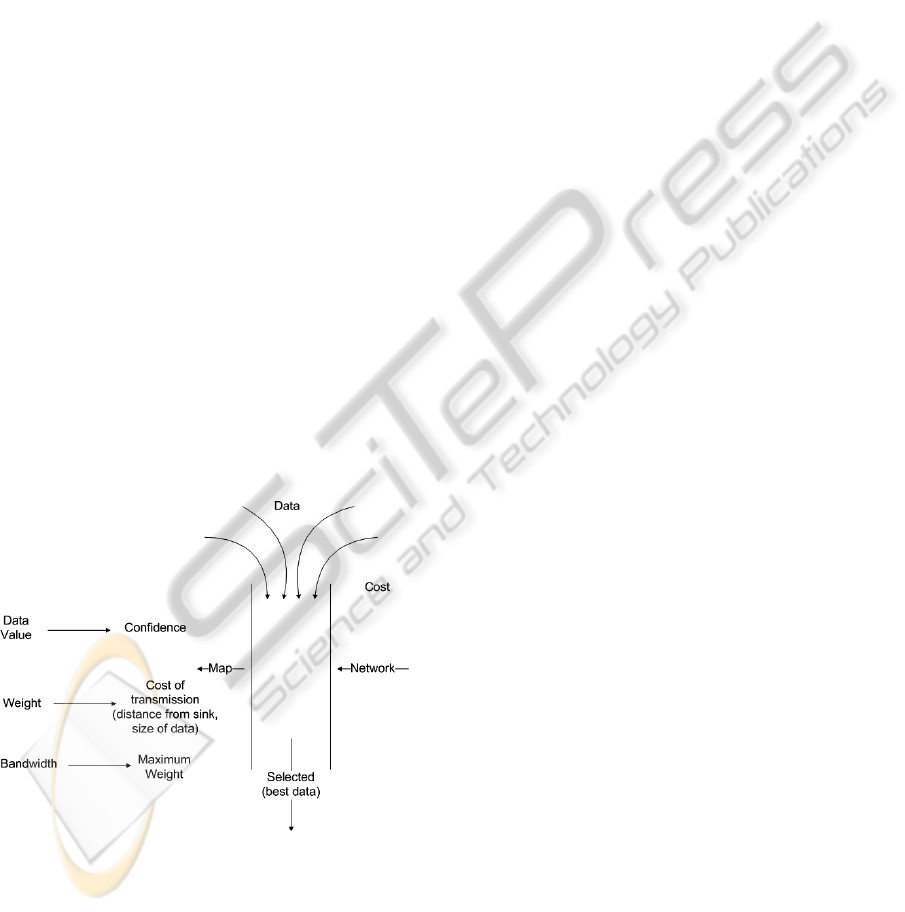
4.2 Phase II Knapsack Optimization

Phase II of our optimal data selection model uses the

data reliabilities assigned in Phase I and the

available bandwidth as input (refer Figure 5). In

OASIS, our resource constrained wireless sensor

network bandwidth was a limiting factor which had

to be conserved. As mentioned above, we had 16

sensor nodes, each of which were attached to

multiple, continuously sampling high fidelity

N2SeismicSensorCorrelation

High

Low

100

Cluster3Correlation

High

Low

98.0

2.00

Cluster3Tremor

Tru e

False

100

0 +

N1SeismicSenorCorrelation

High

Low

100

N10SeismicSensorCorrelation

High

Low

100

N1SeismicDataReliability

Reliable

Unreliable

3.96

96.0

N2SeismicDataReliability

Reliable

Unreliable

98.0

1.96

N10SeismicDataReliability

Reliable

Unreliable

98.0

1.96

N3SeismicDataReliability

Reliable

Unreliable

98.0

1.96

N17SeismicSensorCorrelation

High

Low

100

N17SeismicDataReliability

Reliable

Unreliable

98.0

1.96

N3SeismicSensorCorrelation

High

Low

100

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

sensors. Each sensor node had a seismic, an

infrasonic, and a lightning sensor which were

sampled at a 100Hz, 100Hz, and 10Hz, respectively.

Due to the large amount of data being continuously

sampled and the limited bandwidth that was being

shared between the 16 nodes, it was not possible for

all of the data from all of the nodes to be transmitted

in real-time. The network bandwidth problem was

exasperated by the funnelling of data to a sink point

for transmission to an access point. Therefore, we

had to determine at any specific point in time which

was the “best” data to be sent. To decide what the

“best” data was, we needed to use the confidence

parameters determined by the Bayesian network and

optimize the bandwidth using a 0-1 Knapsack

approach, as shown in Figure 5, and discussed

thoroughly in the remainder of this section.

We used the confidence parameters because they

allowed us to reflect our belief in the correctness or

accuracy of the data in our decision. For example, if

some of the data had a confidence parameter of 15%

we would probably not have wanted to use our

valuable bandwidth to transmit such unreliable data.

The reason that we needed to optimize the

bandwidth and not just “fill up” all of the bandwidth

with the highest priority data was due to the

bandwidth sharing and funnelling effect of the

network topology of our sensor network. Further, we

need to minimize the bandwidth usage (by not

transmitting unreliable data) while maximizing the

return (high priority packets).

Figure 5: Knapsack Optimization.

In general, the knapsack optimization technique

originated from the class of problems using fixed

sized knapsack in which the user wants to carry the

most valuable items while minimizing the weight

that they had to bear. The 0-1 knapsack problem is

the most common type of knapsack problem in

which the number of each item is limited to either 0

or 1. Generally speaking, in a bounded knapsack

problem this number does not have to be limited to

one but may be any integer less than y, as specified

by the user. However, for our scenario each data

stream was unique, we never had duplicates of the

same data stream so it followed that we would use

the 0-1 knapsack approach.

Let us first define a value v

and a weight w

to be

associated with each of the data streams. Further, we

also had to assign a maximum weight, MW which

the entire network could not exceed. In our scenario,

the value, v

, of each item was the confidence

parameter. The weight, w

, associated with each data

stream was the cost of transmission in terms of

bandwidth. Finally, MW was the limiting bandwidth

available within the network. Our goal, which was to

minimize the weight w

while maximizing the value

received v

, is defined formally below in Equation 2

and Equation 3. Note, j

is the number of each of the

data streams which in our scenario was restricted to

0 or 1.

}1,0{∈∀j

(2)

Equation 2: Weight Maximizing.

}1,0{∈∀j

(3)

Note that for n items if we were to use a brute

force technique and compute all possible

combinations of the n data steams then this would

require 2

combinations to be computed. Thus, this

brute force approach has a computational

complexity, which is NP-complete. However, we

use a pseudo-polynomial time dynamic

programming solution, which reduces the

complexity to O(nW), which for known inputs is

weakly NP-complete and can be computed.

We input the confidence parameter and the

available bandwidth into the 0-1 knapsack

optimization algorithm. The output of this algorithm

is the optimum data subset. More specifically this is

a decision regarding the data, some subset i of our

total data set z, that would optimize our resources by

minimizing the cost while maximizing the return.

Thus, in choosing several items, say b items, we had

a choice, we could either add another item, say b+1,

or we could just have b items. If adding the

additional b+1 item would cause the total weight of

the subset, say w

, to exceed the maximum weight

MW then item b+1 could not be added. However, if

∑

≤

MWjw

DATA RELIABILITY AND DATA SELECTION IN REAL TIME HIGH FIDELITY SENSOR NETWORKS

adding item b did not cause MW to be exceeded then

b+1 could be added. We chose to add item b+1 if

adding it would increase the confidence of the subset

(if v

sb+1

> v

), otherwise (if v

sb+1

<= v

) we

excluded it. It should be noted that the algorithm

only determines the maximum confidence that can

be achieved. It does not tell us which items attain

that confidence. In order to get the items we had to

additionally “mark” each item that should be

included. The items that should be included are the

ones that increase the overall confidence of the

subset (this is denoted v

sb+1

> v

). The

implementation is discussed in detail in (Peterson,

2010).

5 EXPERIMENTS AND RESULTS

To provide input to Phase I, we emulated a

continuously changing stream of seismic data which

encompassed the different scenarios that we

expected to see on a volcano. We used 4 different

experimental setups. The first two experiments

consisted of real sensor data (with added tremor

points) while the second two experiments consisted

of random data with randomly occurring tremors and

random data with exponentially occurring tremors,

respectively. We divided each of the four

experiments into six time periods (for a total of 24

time periods), where each period represented a

specific scenario. It was important to use well

controlled data streams in which we knew which

sensors data streams contained bad or erroneous data

to be able to definitively state if the algorithms used

in the evaluations were accurately determining the

reliability.

In the experiments that will be described next,

we use the results from Phase I as input to Phase II

(as depicted in our model) and let the results for the

optimal data selection from both phases be

compared with other schemes, including schemes

that use various threshold values (expert knowledge)

or averaging for data selection.

We used the number of high priority nodes

selected (i.e., the number of high priority, high

reliable data selected) as the metric to measure the

accuracy of our algorithm. In general, our algorithm

selected more optimum nodes than the other

algorithms. We did this by selecting the nodes with

lower bandwidth requirements. Additionally our

algorithm also included additional nodes because we

continued to include nodes in the optimized subset

until we consumed all the remaining bandwidth.

In the previous section, we stated that we used

the individual data streams reliability parameters

from the Bayesian network. However, in our

discussion of the Knapsack implementation we said

that the value v

, of each data stream was the

confidence parameter. This confidence parameter is

a combination of both the reliability parameter and

the seismic data priority of each data stream both of

which are derived from Phase I. We choose to utilize

this in order to assign a seismic data priority to each

data flow. This allowed us to give more importance

to nodes in area(s) where we believed activity

(seismic tremor) was occurring. This was very

important as we were not just interested in the most

reliable data but rather the most significant reliable

data. Thus, we simply combined (through a

summation) the seismic data reliability and the

seismic data priority into one entity, the confidence

parameter, v

. We implemented our algorithm in

MATLAB.

5.1 Experiment Scenarios

In order to evaluate our algorithm, we compared it

with three other commonly used algorithms (Ahmen

et al., 2005) (Bettini et al., 2007). The first algorithm

(referred to as Threshold) used a threshold of 90% as

advised by the Earth Scientists. However, as

discussed in Phase I, a single low value will result in

an average below 90% for the entire cluster. Thus,

we also evaluated using a low threshold of 75% to

accommodate this (referred to as Low Threshold). In

addition we also tested it using the median of all

data values, excluding all values below the median

(referred to as Median). This is a simplified version

of our voting algorithm (from Phase I). We also

made the assumption that all of the algorithms start

selecting the nodes numerically beginning with the

lowest number (for consistency).

As previously stated, our first experiment

consisted of real seismic data “injected” with

seismic tremor points as well as faulty data. We

performed and collected the results for all four

experiments, each having six periods for a total of

96 different results. The trace scenarios for Periods I

– VI are as follows.

| Period I: Tremor detectable by all nodes

| Period II: Tremor detectable by all clusters

y Nodes 8 and 17 produce some erroneous data.

| Period III: Tremor detectable by all clusters

y Nodes 1, 6, 11, 16 some erroneous data

| Period IV: Tremor detectable by Clusters 3 & 4

y Nodes 1,2,3,10,17

y Nodes 4,5,6

| Period V: Tremor detectable by Clusters 3 and 4

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

y Nodes 1, 2, 3, 10, 17 (4 good, 1 bad)

y Nodes 4, 5, 6 (all good nodes)

y Nodes 8, 17 some erroneous data

| Period VI: Tremor detectable by Clusters 3 and 4

y Nodes 1, 2, 3, 10, 17 (4 good, 1 bad)

y Nodes 4, 5, 6 (2 good, 1 bad)

y Clusters 1 and 2 cannot detect tremor and also

each have one node with some erroneous data.

y Nodes 1, 6, 11, 15 erroneous

5.2 Results

For all of the experiments we represented the 16

nodes with their id number in matrix M = [1, 2, 3, 4,

5, 6, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17]. The weights

of the nodes correspond to the bandwidth that was

required to transmit the data from that node to the

sink node (in number of hops) and was given by

weights = [2, 2, 2, 1, 1, 1, 3, 3, 2, 3, 3, 3, 3, 3, 3, 2].

The SeismicDataReliabilty and the

SeismicDataPriority (both resulting from the

Bayesian network in Phase I) were each represented

in a matrix. In the interest of space we will not

display all of the SeismicDataReliabilty and the

SeismicDataPriority matrices. As an example the

matrices for Experiment I, Phase III are:

SeismicDataReliability = [3.96, 98, 98, 70.6, 70.6,

31.4, 90.2, 90.2, 98, 11.8, 90.2, 90.2, 90.2, 90.2,

11.8, 98]

SeismicDataPriority = [0, 100, 100, 100, 100, 0,

100, 100, 100, 0, 100, 100, 100, 100, 0, 100]. These

two matrices were added together to get the resulting

confidence parameter that is used as input into the

algorithms. Confidence parameter = [3.96, 198, 198,

170.6, 170.6, 31.4, 190.2, 190.2, 198, 11.8, 190.2,

190.2, 190.2, 190.2, 11.8, 198].

We used two measures to evaluate the algorithms:

accuracy (explained below) and the percentage of

the optimal data selected. It should be noted that in

our volcanic monitoring scenario all the data is not

treated equal. Rather, some of the data can be

categorized as good or error free data, while other

data is referred to as bad or erroneous data.

Additionally, the good data must further be

categorized as good data which is generated from a

node that is physically located in an area of activity,

and hence has a higher priority or good data that is

generated from a node that is in a non-active area

and has a lower priority. We must adhere to these

distinctions to correctly measure the accuracy of the

algorithms.

We designed a point system to measure the

accuracy of the algorithms such that it reflects the

information related to the type of data selected by

the algorithm. The accuracy of the algorithm is

initially set to 0. Each algorithm is then assigned

points based on the type of node it includes in the

optimal data subset. For each node in the optimal

subset that is erroneous we add “-1” to its current

accuracy. Each good node that is included in the

optimal subset “+1” or “+2” is added to the accuracy

for low priority and the high priority nodes,

respectively.

Figures 6 – 9 show the accuracy of all the

algorithms for time periods I – VI under different

network bandwidths. The available bandwidth refers

to the space available to transmit the data. Thus,

high bandwidth indicates that 83% of the data is

allowed to be transmitted, while medium high,

medium, and low can handle 53%, 26%, and 13% of

allowable data, respectively. In Period I of Figures 6

– 8, all four algorithms performed equally. This was

as expected as this time period contained no activity

and had no erroneous data; rather it was used as a

validity test. When the available bandwidth was low,

Figure 9, we performed better due to our

optimization of the nodes and their associated

bandwidth requirements. In all four figures you can

see that in relation to the other algorithms, ours

showed the most improvement in Periods III, V, and

VI. This is because those were the time period that

contained some erroneous data. Additionally, you

can see that the increase in the amount of accuracy

points that our algorithm gains versus the other

algorithms is inversely related to the available

bandwidth. Thus, while our algorithm never

performed worse than the competition, it displays

the most gains when the bandwidth resources are

restricted and erroneous data is present.

The second metric that we used to evaluate our

optimum data selection algorithm was a measure of

the percentage of the optimal data that was chosen.

By optimal data, we refer to all of the data that does

not contain errors. In order to compute the

percentage, as shown in Figures 10 – 13, we took the

ratio of the total number of good nodes that were

selected in the optimum data set to the total number

of nodes that were in the entire sample. From the

results it is evident that the percentage of increase is

directly proportional to the available bandwidth.

Thus, it is expected that when the bandwidth is

limited, the total number of nodes selected is also

reduced. However we can refer to the relative gain

between algorithms in order to compare their results.

As demonstrated in Figure 10, when the

bandwidth is limited, our algorithm outperformed

others in all cases. Again, it is demonstrated in all of

the figures that we showed the greatest improve-

DATA RELIABILITY AND DATA SELECTION IN REAL TIME HIGH FIDELITY SENSOR NETWORKS

Figure 6: Accuracy for High Bandwidth.

Figure 7: Accuracy for Medium High Bandwidth.

Figure 8: Accuracy for Medium Bandwidth.

Figure 9: Accuracy for Low Bandwidth.

Figure 10: Good Data Selected High Bandwidth.

ments in the periods where there was erroneous data

present. This is particularly important because this

algorithm is not necessary if none of the data was

erroneous or if the bandwidth was such that all of

the data could be select. Rather it is when the

bandwidth is restricted and the data is not all good

that we require optimization of the subset selection

algorithm.

Figure 11: Good Data Selected Medium High Bandwidth.

Figure 12: Good Data Selected Medium Bandwidth.

Figure 13: Good Data Selected Low Bandwidth.

6 CONCLUSIONS

AND FUTURE WORK

Optimal data selection has become an important

issue in environment monitoring, where high-

fidelity, continuous data samples are used. We

designed, implemented, and tested our optimal data

selection model system for wireless sensor networks.

Our model is composed of two phases: one to

identify the confidence in the data and second to

optimize the selection of the data based on its

reliability and availability of network bandwidth.

Our analysis showed that when compared to other

algorithms, our optimal data selection model was

able to significantly outperform existing algorithms.

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

While we implemented and tested our algorithm

in a volcanic monitoring scenario, our work is not

constrained to this arena. The proposed optimal data

selection model is ideally suited to many resource

constrained wireless sensor networks where data

quality and data selection are important. Further, we

are extending this optimal data selection model into

a larger context modeling framework that also

determines when a tremor occurs, as opposed to

other events such as a rock falling, and its location.

REFERENCES

Ahmen, B., Lee, Y-K., Lee, S., Zhung, Y., 2005. ‘Scenario

Based Fault Detection in Context-Aware Ubiquitous

Systems using Bayesian Networks’, Computational

Intelligence for Modelling , Control and Automation,

pp. 414-420.

Bettini, C., Brdiczka, O., Henricksen, K., Indulska, J.,

Nicklas, D., Ranganathan, A., Riboni, D., 2009. ‘A

survey of context modelling and reasoning

techniques’Pervasive and Mobile Computing, pp. 161-

180.

Bettini, C., Maggiorini, D., Riboni, D., 2007. ‘Distributed

Context Monitoring for the Adaptation of Continuous

Services’, World Wide Web, Springer Netherlands.

Kumar, et al., 2003. ‘PICO: A Middleware Framework for

Pervasive Computing’, IEEE Pervasive Computing,

pp. 72-79.

Survey, U.S. Geological. www.usgs.gov/

Lee, D., Meier, R., 2007. ‘Primary-Context Model and

Ontology: A Combined Approach for Pervasive

Transportation Services’, IEEE Pervasive Computing

and Communications Workshops, pp. 419-424.

Peterson, N., 2010. ‘Adaptive Context Modeling and

Situation Awareness for Wireless Sensor Networks’,

Ph.D. dissertation, Dept. Elect. Eng. and Competer

Science, Washington State Univ., Pullman, WA.

Peterson N., et al., 2008. ‘Tiny-OS Based Quality of

Service Management in Wireless Sensor Networks’,

Hawaii International Conference on System Sciences,

pp. 1-10.

Song, W., et al., 2008. ‘Optimized Autonomous Space In-

situ Sensor-Web for Volcano Monitoring’, IEEE

Journal of Selected Topics in Earth Observations and

Remote Sensing, pp. 1-10.

DATA RELIABILITY AND DATA SELECTION IN REAL TIME HIGH FIDELITY SENSOR NETWORKS