METHOD OF EXTRACTING INTEREST POINTS BASED ON

MULTI-SCALE DETECTOR AND LOCAL E-HOG DESCRIPTOR

Manuel Grand-brochier, Christophe Tilmant and Michel Dhome

Laboratoire des Sciences et Matriaux pour l’Electronique, et d’Automatique (LASMEA)

UMR 6602 UBP-CNRS, 24 avenue des Landais, 63177 Beaumont, France

Keywords:

Multi-scales analysis, Local descriptor, Robustness to image transformations, Elliptical-HOG.

Abstract:

This article proposes an approach to extraction (detection and description) of interest points based Fast-Hessian

and E-HOG. SIFT and SURF are the two most used methods for this problem and their studies allow us to

understand their construction and extract the various advantages (invariances, speeds, repeatability). Our goal

is, ﬁrstly, to couple these advantages to create a new system (detector, descriptor and matching) and, secondly,

to determine the characteristic points for different applications (image transformation, 3D reconstruction...).

Our system must also be as invariant as possible for the image transformation (rotations, scales, viewpoints

for example). Finally, we have to ﬁnd a compromise between a good matching rate and the number of points

matched. All the detector and descriptor parameters (orientations, thresholds, analysis shape) will be also

detailed in this article.

1 INTRODUCTION

There are a large number of applications based on im-

age analysis, especially 3D reconstruction problems,

tracking or pattern recognition for example. These ap-

plications need data usually extracted with two tools:

the detection of interest points (Li and Allison, 2008)

and the local description (Li and Allison, 2008) of

these. The detector analyses the image to extract

the characteristic points (corners, edges, blobs). The

neighborhood study allows us to create a local points

descriptor, in order to match them. For matched in-

terest points, the robustness of various transforma-

tions of the image is very important. To be robust to

scale, interest points are extracted with a global multi-

scales analysis, we considered the Harris-Laplace de-

tector (Harris and Stephens, 1988; Mikolajczyk and

Schmid, 2004b; Mikolajczyk and Schmid, 2002), the

Fast-Hessian (Bay and al., 2006) and the difference

of Gaussians (Lowe, 1999; Lowe, 2004). The de-

scription is based on a local exploration of interest

points to represent the characteristics of the neighbor-

hood. In comparative studies (Choksuriwong and al.,

2005; Mikolajczyk and Schmid, 2004a; Bauer and al.,

2007), it is shown that oriented gradients histograms

(HOG) give good results. Among the many meth-

ods using HOG, we retain SIFT (Scale Invariant Fea-

ture Transform) (Lowe, 1999; Lowe, 2004) and SURF

(Speed Up Robust Features) (Bay and al., 2006), us-

ing a rectangular neighborhood exploration (R-HOG:

Rectangular-HOG). We also mention GLOH (Gra-

dient Location and Orientation Histogram) (Mikola-

jczyk and Schmid, 2004a; Dalal and Triggs, 2005)

and Daisy (Tola et al., 2008), using circular geometry

(C-HOG: Circular-HOG). To provide the best possi-

ble list of points for different applications, we pro-

pose to create a system of detection and local de-

scription which is the most robust possible against the

various transformations that can exist between two

images (illumination, rotation, viewpoint for exam-

ple). It should also be as efﬁcient as possible as re-

gards the matching rate. Our method relies on a Fast-

Hessian points detector, an elliptical exploration and a

local descriptor based E-HOG (Elliptical-HOG). We

propose to estimate local orientation, with the study

of the Harris matrix, in order to adjust the descrip-

tor (rotation invariance) and ﬁnally we will normalize

(brightness invariance).

Section 2 presents brieﬂy SIFT and SURF, and

lists the advantages of each. The various tools and

their parameters (orientations, thresholds, analysis

pattern) we use are detailed in Section 3. To com-

pare our approach to SIFT and SURF, many tests have

been carried out. A synthesis of the different results

is presented in Section 4.

Grand-brochier M., Tilmant C. and Dhome M..

METHOD OF EXTRACTING INTEREST POINTS BASED ON MULTI-SCALE DETECTOR AND LOCAL E-HOG DESCRIPTOR.

DOI: 10.5220/0003369300590066

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 59-66

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

In order to propose a robust method and giving many

interest points, Lowe propose a new approach, SIFT

(Lowe, 1999; Lowe, 2004), consisting of a difference

of Gaussians (DoG) and R-HOG analysis. The de-

tector is based on an approximation of the Laplacian

of Gaussian (Lindeberg, 1998) and interest points are

obtained by maximizing the DoG:

D(x, y, σ) =(G(x, y, kσ) −G(x, y, σ)) ∗I(x, y)

L(x, y, kσ) −L(x, y, σ).

(1)

The descriptor uses an orientation histogram, based

on equation 2, to determine the angle of rotation θ to

be applied to the mask analysis.

θ(x, y) = tan

−1

(

(L(x, y + 1) −L(x, y −1)

(L(x + 1, y) −L(x −1, y)

) (2)

It then uses R-HOG, formed by local gradients in the

neighborhood, previously smoothed by a Gaussian.

Finally, the descriptor is normalized to be invariant

to illumination changes.

An extension of SIFT, GLOH (Mikolajczyk and

Schmid, 2004a; Dalal and Triggs, 2005), has been

proposed to increase the robustness. It amounts to

the insertion of a grid in log polar localization. The

mask analysis of this descriptor is composed of three

rings (C-HOG), whose two largest are divided along

eight directions. More recently, the descriptor Daisy

(Tola et al., 2008) has been proposed. It is also based

on a circular neighborhood exploration and constructs

convolved orientation maps.

SIFT has not a fast computational speed. SURF

(Bay and al., 2006) proposes a new approach, whose

main objective is to accelerate the various image pro-

cessing steps. The ﬁrst problem was to choose the

detector method. The various tests (Juan and Gwun,

2009; Bay and al., 2006) show that the Fast-Hessian

has the best repetability rate. It is based on the Hes-

sian matrix:

H(x, y, σ) =



(x, y, σ) L

(x, y, σ)

(x, y, σ) L

(x, y, σ)



, (3)

with L

i j

(x, y, σ) the second derivative in the directions

i and j of L. The maximization of its determinant

(Hessian) allows us to extract the coordinates of in-

terest points in a given scale. The second step, the

local description, is based on Haar wavelets. These

estimate the local orientation of the gradient, allow-

ing the construction of the descriptor. Finally, SURF

studied the sign of the wavelet transform to increase

the quality of results.

The presented methods use similar tools: multi-

scale analysis (Fast-Hessian or DoG), local descrip-

tion based HOG, local smoothing and descriptor nor-

malization. For matching they use a minimization

of either the Euclidean distance between descrip-

tors (SURF) or the angle between vectors descriptors

(SIFT). Many tests (Mikolajczyk and Schmid, 2004a;

Juan and Gwun, 2009; ?) can establish a list of dif-

ferent qualities of each. It follows that SURF, with

its detector, has the best repeatability for viewpoint

changes, scale, noise and lighting. It is also faster

than SIFT, however it has a higher precision rate for

rotations and scale changes. It has also a higher num-

ber of detected points for all transformations. It might

be interesting to combine these two methods.

3 METHOD

The method we propose is divided into three parts: a

Fast-Hessian multi-scale detector, a local E-HOG de-

scriptor and an optimized matching. This section de-

scribes the different steps of our method and param-

eters used. The detector Fast-Hessian provides a list

of interest points, characterized by their coordinates

and local scale. Our descriptor is based on the Harris

matrix interpretation, and the construction of E-HOG.

Matching is based on an approximation of the nearest

neighbors and removing duplicates. These issues will

be detailed below.

3.1 Detection

The Fast-Hessian is an approximated method of Hes-

sian matrix (equation 3), to reduce the computing

time. This detector uses integral images (Figure 1),

therefore it takes only three additions and four mem-

ory accesses to calculate the sum of intensities inside

a rectangular region of any size. The Fast-Hessian

Figure 1: Determination of integral image.

relies on the exploitation of the Hessian matrix (equa-

tion 3), whose determinant is calculated as follows:

det(H(x, y, σ)) =

(x, y, σ)L

(x, y, σ) −L

(x, y, σ)),

(4)

where L

(x, y, σ) is the convolution of the Gaus-

sian second order derivative

∂

∂x

g(σ) with the im-

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

age I in point (x, y), and similarly for L

(x, y, σ) and

(x, y, σ). Gaussians are optimal for scale-space

analysis and the Fast-Hessian provides an approxima-

tion of these second order derivative (Figure 2).

Figure 2: Top row: Gaussian second order partial deriva-

tives, bottom row: approximation for the second order

Gaussian partial derivatives.

By looking for local maxima of the determinant,

we establish a list of K points associated with a scale,

denoted {(x

, y

, σ

); k ∈[[0;K −1]]}, where:

, y

, σ

) = argmax

{x,y,σ}

(det(H(x, y, σ))). (5)

The number of interest points obtained depends on the

space scale explored and thresholding of local max-

ima. We have to ﬁnd a compromise between scale

space exploration and relevance of extracted points.

The inﬂuence of this one will be detailed in Section 4.

3.2 Description

As with SIFT and SURF, our method is based on

HOG, yet our analysis window will consist of ellipses

(E-HOG). Different tools will also be necessary to ad-

just and normalize our descriptor.

3.2.1 Determining the Local Orientation

Gradient

To be as invariant as possible for rotations, estimat-

ing the local orientation gradient of the interest point

is necessary. This parameter allows us to adjust the

E-HOG, giving an identical orientation for two corre-

sponding points. For this, we use the Harris matrix,

calculated for each point (x

, y

) and deﬁned by:

, y

) =

∑

V (x

)

, y

)]

∑

V (x

)

, y

)

∑

V (x

)

, y

)

∑

V (x

)

, y

)]

(6)

where V (x

, y

) represents the neighborhood of the in-

terest point, I

and I

are the ﬁrst derivatives in x and

y of image, calculated using the Canny-Deriche oper-

ator. The properties of this matrix can study the infor-

mation dispersion. The local analysis of its eigenvec-

tors (

−→

and

−→

) associated with corresponding eigen-

values can extract an orientation estimate:

∆ = Trace(M

, y

))

−4Det(M

, y

))

Trace(M

, y

)) +

√

∆

−→







(

∑

V (x

)

)]

)−λ

∑

V (x

)







= arctan(

−→

). (7)

3.2.2 Descriptor Construction

The initial shape of our descriptor relies on a circular

neighborhood exploration of the interest point. The

seventeen circles used, are divided into three scales

(Figure 3) and are adjusted by θ

(equation 7).

Figure 3: Initial mask analysis of our descriptor, centered at

, y

) and oriented by an angle θ

This angle allows us to be robust to image rotation.

The circle diameter is proportional to σ

, thus accen-

tuating the scale invariance. To manage the prob-

lem of viewpoint changes and anisotropic transforma-

tions, we propose to modify the shape of our descrip-

tor. The goal is to get local information more consis-

tently. We propose to use an elliptical exploration to

describe the neighbor of interest points (Figure 4).

An analysis of the properties of afﬁne detectors

(Mikolajczyk and Schmid, 2004b; Mikolajczyk and

al., 2005) allows us to determine the ratio r

between

the axes of ellipses. For example for the Harris afﬁne

detector, two scales are used and are bound by the

following equation: σ

= sσ

where σ

is the differ-

entiation scale, σ

is the integration scale and s is the

ratio. It is noted that s is generally between 0.5 and

METHOD OF EXTRACTING INTEREST POINTS BASED ON MULTI-SCALE DETECTOR AND LOCAL E-HOG

DESCRIPTOR

Figure 4: Final mask analysis of our descriptor, centered at

, y

) and oriented by an angle θ

Figure 5: Example of local description of interest points.

0.75. By the parallelism between these two scales and

our ellipses, it is possible to determine the best ratio

. Based on many tests, the ratio giving the best re-

sult is equal to 0.5. Figure 5 illustrates the construc-

tion of our ellipses (for better visualization, we only

show the central ellipse of each descriptor).

We construct a HOG eight classes (in steps of 45)

for each ellipse. Our descriptor, we note des

, y

belongs to R

136

(17 ellipses × 8 directions). To be

invariant for brightness changes, histogram is normal-

ized and we use also a threshold for E-HOG to remove

the high values of gradient.

3.3 Matching

The objective is to ﬁnd the best similarity (corre-

sponding to the minimum distance) between descrip-

tors of two images. Euclidean distance, denoted d

between two descriptors is deﬁned by:

(des

), des

, y

)) =

[des

, y

)]

·des

, y

(8)

The minimization of d

, denoted d

min

, provides a pair

of points {(x

, y

);(x

, y

)}:

l = argmin

l∈[[0;L−1]]

(des

, y

), des

, y

))), (9)

min

= d

(des

, y

), des

, y

)). (10)

To simplify the search for this minimum distance,

we propose to use an approximative nearest neigh-

bor search method (a variant of k-d tree) (Arya and

al., 1998). The principle is to create a decision tree

based on descriptors components of the second image

(Figure 6). So, for each new descriptor of the ﬁrst im-

Figure 6: Example of decision tree to extract the nearest

neighbors.

age, all components are tested and the nearest neigh-

bor is deﬁned. Research is therefore faster, without

sacriﬁcing precision. To have a more robust match-

ing, thresholding is applied to this distance, to ﬁnd a

``high´´minimum. The pair of points is valid if:

min

≤ α ×min(d

(des

, y

), des

, y

))), (11)

for l ∈[[0; N −1]]\

l and with α the threshold selection

(detailed in Section 4). We do not allow a point to

match with several other points, and a ﬁnal step is to

remove duplicates.

4 RESULTS

We are going to compare our method with SIFT and

SURF. These two methods are the most used and give

the best results. We propose to study the matching

rate and the precision of each of them. We will also

study the recall = f (1 −precision) curves and the es-

timation error of the transformed image.

4.1 Databases

To validate our method, we chose two databases:

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

• The ﬁrst one, noted ODB and extracted from the

Oxford

database, proposes scene transforma-

tions with an access to the matrix of homography.

Transformations studied are brightness changes

(ODB

), modiﬁed jpeg compressions (ODB

blur (ODB

), rotations and scales (ODB

), and

small and large angle viewpoint changes (respec-

tively ODB

and ODB

). Figure 7 illustrates this

database.

ODB

Figure 7: Examples of images used for transformations:

(top: left to right) brightness changes, modiﬁed jpeg com-

pressions, blur, (bottom: left to right) rotations + scales,

viewpoint changes (small angle), and viewpoint changes

(large angle).

• A second database, noted SDB, composed of a

set of synthetic image transformations (Figure 8

and Figure 9). These transformations are rota-

tions 45 (SDB

), scales (SDB

), anisotropic scales

(SDB

), rotations 45 + scales (BS

) and rotations

45 + anisotropic scales (BS

ras

SDB

Figure 8: Examples of laboratory images (board cameras)

used for synthetic transformations.

http://www.robots.ox.ac.uk/∼vgg/data/data-aff.html

SDB

ras

SDB

Figure 9: Examples of internet images (Pig, Lena, Beatles)

used for synthetic transformations.

4.2 The Parameters of our Method

4.2.1 Inﬂuence of the Number of Octave

(Detection Parameter)

To get the best compromise between relevance and

number of extracted points, we use the following

curves:

Figure 10: These graphs represent, for ODB

images: (top)

the correct matching rate according to the number of octave

and (bottom) the number of points that can be matched.

It represents, on one hand the matching precision

for ODB

images, on the other hand the number of

points that can be matched. The best compromise is

two octaves, it has better precision than three or four

octaves while keeping an almost identical number of

points. One octave has a better precision than two

octaves, but loses a lot of points. Therefore we choose

two octaves instead of four used by SURF.

4.2.2 Threshold Selection

The threshold selection α used in the equation 11 is

determinated by analysing the curves of Figure 11.

This threshold allows us to increase the selectivity,

METHOD OF EXTRACTING INTEREST POINTS BASED ON MULTI-SCALE DETECTOR AND LOCAL E-HOG

DESCRIPTOR

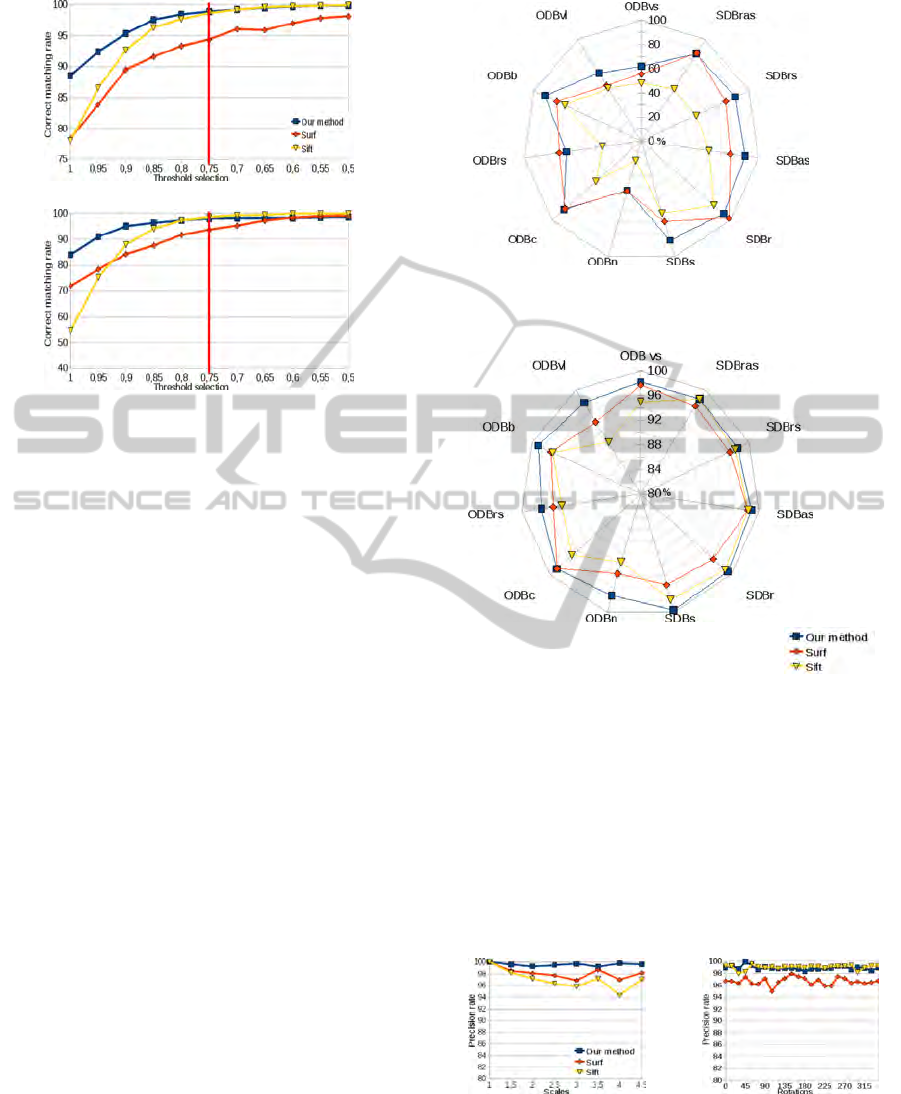
Figure 11: These graphs represent the correct matching rate

according to the threshold selection. Top is for viewpoint

changes (graﬁti 1 → 2) and bottom is for rotation + scale

(boat 1 → 3).

but the consequence is a reduction in the number of

matched points.

If the threshold goes away from 1, the matching

becomes more selective and therefore fewer points are

used. The problem is to ﬁnd the best compromise be-

tween the correct matching rate and the number of

matched points. SIFT recommands a threshold of 0.8

and SURF a threshold of 0.7. By analysing curves of

Figure 11, we choose a threshold α = 0.75.

4.3 Evaluation Tests and Results

4.3.1 Matching Rate and Precision

We propose to compare the matching rate T

, as well

as the precision P of every method. T

is deﬁned by

the number of correct matches divided by the num-

ber of possible matches. P is deﬁned by the number

of correct matches divided by the number of matches

performed. A synthesis of the results obtained is pro-

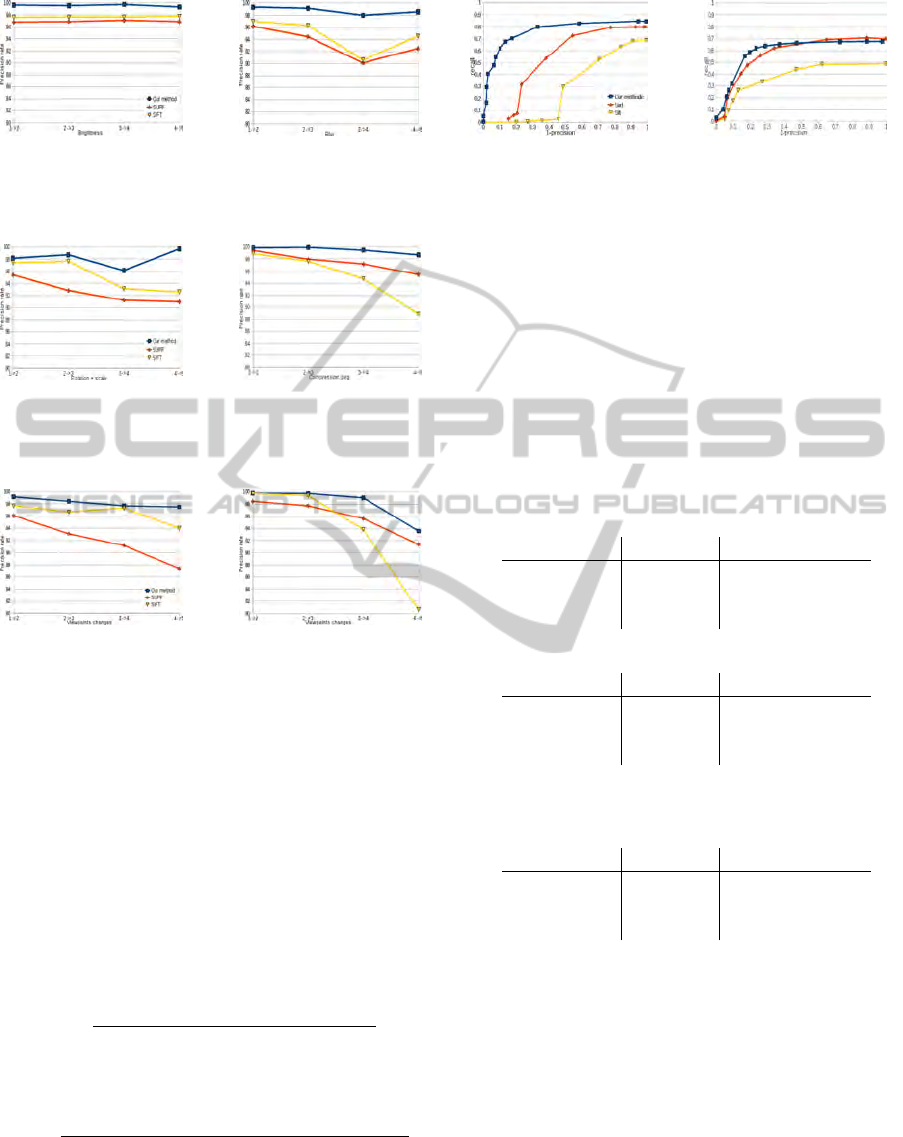
posed in Figure 12.

Our method presents results better or as good as

SIFT and SURF. Our matching rate remains better

than the two other methods with the exception of the

databases ODB

and SDB

transformations. Never-

theless the difference between SURF and our method

for this type of transformation is lower than 4%. For

other type of transformation, the biggest differences

are observed for rotation 45 + scale (≈ 10% between

our method and SURF and 37% with SIFT) and for

large angle viewpoint changes (≈ 18% with SURF

and SIFT). Our matching precision is also better and

Figure 12: These graphs represent at top: a matching rate

and at bottom: a matching precision. Matching rate is the

ability to match points and matching precision is the match

quality. The goal is to have the highest rate of correctly

matched points (with better precision).

remains constantly above 95%. The biggest differ-

ence is obtained for large angle viewpoint changes

(4% for SURF and 8% for SIFT). To detail the preci-

sion curves of different methods, we propose graphs

in Figures 13 to 16.

(a) (b)

Figure 13: (a) precision rate for scales changes (SDB

) and

(b) precision rate for rotations (SDB

These curve show a better precision rate for our

method, or similar for rotation transformations (ﬁgure

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

(a) (b)

Figure 14: (a) precision rate for brightness (ODB

) and (b)

precision rate for blur (ODB

(a) (b)

Figure 15: (a) precision rate for rotation and scale (ODB

)

and (b) precision rate for compression jpeg (ODB

(a) (b)

Figure 16: (a) and (b) precision rate for viewpoints changes

respectively (ODB

) and (ODB

13.b). Another observation can be made through the

transformations studied, concerning the stability of

our method. Indeed, our curves decrease more slowly

than SIFT and SURF, implying a precision rates more

constant.

4.3.2 Inﬂuence of Data

To observe the inﬂuence of data on different methods,

we use the recall = f (1 −precision) curves (Mikola-

jczyk and Schmid, 2004a) with two components come

from:

recall =

number of correct matches

number of possible correct matches

and

1 −precision =

number of false matches

number of (correct matches + false matches

We propose to analyse two curves (Figure 17) and we

can observe that our method is more stable than SIFT

and SURF. Therefore, our method is more robust to

the deterioration of data for these transformations.

(a) (b)

Figure 17: (a) a recall versus 1-precision for brightness

(ODB

: 1→ 4) and (b) a recall versus 1-precision for ro-

tation + scale (ODB

: 2→ 4).

4.3.3 Estimation of the Image Transformation

We propose a ﬁnal study on the estimation of the ho-

mography matrix. For 3D reconstruction, for exam-

ple, the estimate of this matrix is very important, and

the goal is to have the best estimation (the error as low

as possible) with maximum points validating this ma-

trix. The estimation is based on the matches and the

Ransac algorithm. We studied three transformations

and the results are:

• viewpoints changes (ODB

error (%) valid points (%)

Our method 0.06 96.72

SURF 3.46 96.34

SIFT 2.98 92.35

• rotation and scale (ODB

error (%) valid points (%)

Our method 0.54 93.23

SURF 1.69 86.03

SIFT 2.06 88.24

• blur (ODB

error (%) valid points (%)

Our method 0.61 97.13

SURF 0.66 92.1

SIFT 0.58 96.56

Our method obtains, for the ﬁrst two transformations,

an error rate below SIFT and SURF and a higher rate

of valid points. For the last transformation, the results

are similar for all three methods.

5 CONCLUSIONS

In this article we presented a method based on, on the

one hand the avantages of SIFT and SURF (repetabil-

ity, invariances) and on the other hand the use of tools

such as the Harris matrix, the HOG or the decision

tree. Detection relies on Fast-hessian detector that we

METHOD OF EXTRACTING INTEREST POINTS BASED ON MULTI-SCALE DETECTOR AND LOCAL E-HOG

DESCRIPTOR

thresholded. Description interprets the Harris matrix

and uses an elliptical shape to adapt the descriptor

to the image transformation. Finally, matching cre-

ates decision tree and removes duplicates. To vali-

date our method, we compared it to SIFT and SURF.

Our method has better matching rate and better preci-

sion for most transformations. It is also robust to data

degradation problems and provides an estimation of

homography matrix more reliable, keeping good rate

of valid points. Therefore data extracted from im-

ages are better and will result in an improvement of

the applications referred (3D reconstruction or pattern

recognition for example).

Our prospects are a generalization of our method,

with application to a spatio-temporal analysis. We

will add a temporal variable to the Hessian matrix

(equation 3). We also transform our descriptor shape

to obtain an neighborhood exploration ellipsoidal (for

tracking for example). An other prospect is to inte-

grate a third dimension to use it in medical imaging.

REFERENCES

Arya, S., Mount, D., Netanyahu, N., Silverman, R., and

Wu, A. (1998). An optimal algorithm for approxi-

mate nearest neighbor searching in ﬁxed dimensions.

J.ACM, 45:891–923.

Bauer, J., Snderhauf, N., and Protzel, P. (2007). Compar-

ing several implementations of two recently published

feature detectors. Intelligent Autonomous Vehicles.

Bay, H., Tuylelaars, T., and Gool, L. V. (2006). Surf :

Speeded up robust features. European Conference on

Computer Vision.

Choksuriwong, A., Laurent, H., and Emile, B. (2005).

Etude comparative de descripteur invariants d’objets.

ORASIS.

Dalal, N. and Triggs, B. (2005). Histograms of oriented

gradients for human detection. IEEE Conference on

Computer Vision and Pattern Recognition.

Harris, C. and Stephens, M. (1988). A combined corner and

edge detector. Alvey Vision Conference, pages 147–

151.

Juan and Gwun (2009). A comparison of sift, pca-sift

and surf. International Journal of Image Processing,

3(4):143–152.

Li, J. and Allison, N.M. (2008). A Comprehensive Review

of Current Local Features for Computer Vision. Neu-

rocomputing, 71(10-12):1771–1787.

Lindeberg, T. (1998). Feature detection with automatic

scale selection. International Journal of Computer Vi-

sion, 30(2):79–116.

Lowe, D. (1999). Object recognition from local scale-

invariant features. IEEE International Conference on

Computer Vision, pages 1150–1157.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91–110.

Mikolajczyk, K., and Schmid, C. (2002). An afﬁne invari-

ant interest point detector. European Conference on

Computer Vision, 1:128–142.

Mikolajczyk, K. and Schmid, C. (2004a). A performance

evaluation of local descriptors. IEEE Pattern Analysis

and Machine Intelligence, 27(10):1615–1630.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaffalitzky, F., Kadir, T., and Van Gool, L.

(2005). A comparaison of afﬁne region detectors. In-

ternational Journal of Computer Vision, 65(1/2):43–

72.

Mikolajczyk, K. and Schmid, C. (2004b). Scale & afﬁne in-

variant interest point detectors. International Journal

of Computer Vision, 1(60):63–86.

Tola, E., Lepetit, V., and Fua, P. (2008). A fast local descrip-

tor for dense matching. IEEE Conference on Com-

puter Vision and Pattern Recognition.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications