ADABOOST GPU-BASED CLASSIFIER

FOR DIRECT VOLUME RENDERING

Oscar Amoros

, Sergio Escalera

and Anna Puig

Barcelona Supercomputing Center - CNS, K2M Building, c/ Jordi Girona, 29 08034 Barcelona, Spain

UB-Computer Vision Center, Campus UAB, Ediﬁci O, 08193, Bellaterra, Barcelona, Spain

WAI-MOBIBIO Research Groups, University of Barcelona, Avda.Corts Catalanes, 585, 08007 Barcelona, Spain

Keywords:

Volume rendering, High-performance Computing and parallel rendering, Rendering hardware.

Abstract:

In volume visualization, the voxel visibility and materials are carried out through an interactive editing of

Transfer Function. In this paper, we present a two-level GPU-based labeling method that computes in times

of rendering a set of labeled structures using the Adaboost machine learning classiﬁer. In a pre-processing

step, Adaboost trains a binary classiﬁer from a pre-labeled dataset and, in each sample, takes into account a

set of features. This binary classiﬁer is a weighted combination of weak classiﬁers, which can be expressed as

simple decision functions estimated on a single feature values. Then, at the testing stage, each weak classiﬁer

is independently applied on the features of a set of unlabeled samples. We propose an alternative represen-

tation of these classiﬁers that allow a GPU-based parallelizated testing stage embedded into the visualization

pipeline. The empirical results conﬁrm the OpenCL-based classiﬁcation of biomedical datasets as a tough

problem where an opportunity for further research emerges.

1 INTRODUCTION

The deﬁnition of the visibility and the optical proper-

ties at each volume sample is a tough and non intuitive

user guided process. It is often performed through

the user deﬁnition of Transfer Functions (TF). Selec-

tion of regions is deﬁned indirectly by assigning to

zero the opacity since totally transparent samples do

not contribute to the ﬁnal image. The use of TFs al-

lows to store them as look-up tables (LUT), directly

indexed by the intensity data values during the vi-

sualization, which signiﬁcantly speeds up rendering

and it is easy to implement in GPUs. In previous

works, the transfer function is broken into two sepa-

rated steps (Cerquides et al., 2006): the Classiﬁcation

Function (CF) and the optical properties assignment.

The Classiﬁcation Function determines at each point

inside the voxel model at which speciﬁc structure the

point belongs. Next, the optical properties assignment

is a simple mapping that assigns to each structure a

set of optical properties. In this approach, we focus

on the deﬁnition and the improvement of the Classiﬁ-

cation Function and its integration into the rendering

process. The main advantage of the classiﬁcation ap-

proach is that, since a part of the classiﬁcation can be

carried on a pre-process, before rendering, it can use

more accurate and computationally expensive classi-

ﬁcation methods than transfer functions mappings.

Speciﬁcally, we use a learning-based classiﬁca-

tion method that splits into two steps: learning and

testing. In the learning step, given a set of train-

ing examples, each marked by an end-user as belong-

ing to one of the set of the labels or categories, the

Adaboost-based Machine Learning training algorithm

builds a model, or classiﬁer, that predicts whether a

new voxel falls into one category or the other. In the

testing stage, the classiﬁer is used to classify a new

voxel description. Thus, the learning step is done in

a pre-process stage, though the testing step is inte-

grated on-the-ﬂy into the GPU-based rendering. In

the rendering step, at each voxel value, the classiﬁer

is applied to obtain a label. We propose a GPGPU

strategy to apply the classiﬁer, interpret the voxels as

the set of objects to classify, and their property values,

derivatives and positions as the attributes or features

to evaluate. We apply a well-known learning method

to a sub-sampled set of already classiﬁed voxels and

next we classify a set of voxel models in a GPU-based

testing step. Our goal is three-fold:

• to deﬁne a voxel classiﬁcation method based on a

215

Amoros O., Escalera S. and Puig A..

ADABOOST GPU-BASED CLASSIFIER FOR DIRECT VOLUME RENDERING.

DOI: 10.5220/0003369902150219

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 215-219

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

powerful machine learning approach,

• to deﬁne a GPGPU-based testing stage of the pro-

posed classiﬁcation method integrated to the ﬁnal

rendering,

• to analyze the performance of our method com-

paring ﬁve different implementations with differ-

ent public data sets on different hardware.

2 ADABOOST CLASSIFIER

In this paper, we focus on the Discrete version of Ad-

aboost, which has shown robust results in real ap-

plications (Friedman et al., 1998). Given a set of N

training samples (x

, y

), .., (x

, y

), with x

a vector

valued feature and y

= −1 or 1, we deﬁne F(x) =

∑

(x) where each f

(x) is a classiﬁer produc-

ing values ±1 and c

are constants; the correspond-

ing prediction is sign(F(x)). The Adaboost procedure

trains the classiﬁers f

(x) on weighted versions of

the training sample, giving higher weights to cases

that are currently misclassiﬁed. This is done for a se-

quence of weighted samples, and then the ﬁnal clas-

siﬁer is deﬁned to be a linear combination of the clas-

siﬁers from each stage. For a good generalization of

F(x), each f

(x) is required to obtain a classiﬁcation

prediction just better than random (Friedman et al.,

1998). Thus, the most common ”weak classiﬁer” f

is the ”decision stump”. Stumps are single-split trees

with only two terminal nodes. If the decision of the

stump obtains a performance inferior to 0.5 over 1, we

just need to change the polarity of the stump, assur-

ing a performance greater (or equal) to 0.5. Then, for

each f

(x) we just need to compute a threshold value

and a polarity to take a binary decision, selecting that

one that minimizes the error based on the assigned

weights.

In Algorithm 1, we show the testing of the ﬁnal de-

cision function F(x) =

∑

(x) using the Discrete

Adaboost algorithm with Decision Stump ”weak clas-

siﬁer”. Each Decision Stump f

ﬁts a threshold T

and a polarity P

over the selected m-th feature. In

testing time, x

corresponds to the value of the fea-

ture selected by f

(x) on a test sample x. Note that c

value is subtracted from F(x) if the hypothesis f

(x)

is not satisﬁed on the test sample. Otherwise, positive

values of c

are accumulated. Finally decision on x is

obtained by sign(F(x)).

We propose to deﬁne a new and equivalent repre-

sentation of c

and |x| that facilitate the paralleliza-

tion of the testing. We deﬁne the matrix V

(x)

of size

3 × (|x| · M), where |x| corresponds to the dimension-

ality of the feature space. First row of V

(x)

codiﬁes

the values c

for the corresponding features that have

been considered during training. In this sense, each

position i of the ﬁrst row of V

(x)

contains the value

for the feature mod(i, |x|) if mod(i, |x|) 6= 0 or |x|,

otherwise. The next value of c

for that feature is

found in position i + |x|. The positions corresponding

to features not considered during training are set to

zero. The second and third rows of V

(x)

for column

i contains the values of P

and T

for the correspond-

ing Decision Stump. Thus, each “weak classiﬁer” is

codiﬁed in a channel of a 1D-Texture, respectively.

As our main goal is to have real time test-

ing, we deal with two main possibilities: a

GLSL-programmed method on the fragment shader

and an OpenCL/CUDA implementation using the

OpenCL/CUDA-GL integration. We choose OpenCL

for portability reasons. Using GLSL, the gradient cal-

culation habitually is computed on CPU because it’s

faster. Then the results are send to the GPU as shown

in Figure 1. The testing and visualization stages can

be computed into the fragment shader to obtain good

speedups. Through OpenCL, in contrast to GLSL,

we can control almost all the hardware so we can

solve the gradient problem faster in the GPU using

an adaptation of the Micikevicius algorithm (Micike-

vicius, 2009). Thus, the gradient calculation and the

classiﬁcation steps can be computed into the GPU re-

ducing the PCIe transfers and computing each step

faster. In the OpenGL side we use a 3D Texture Map

to visualize the models. The integration of OpenCL

and OpenGL allows to avoid sending the OpenCL la-

beled voxel model back to the Host and visualize it di-

rectly. The OpenGL layer loads the data to the graph-

ics card and then OpenCL obtains the ownership of

the data from the global memory, processes it and re-

turns ownership to OpenGL when ﬁnished.

3 GPGPU IMPLEMENTATION:

INTRODUCING WORK GROUP

SHARING

As shown in Figure 1, we propose two OpenCL ker-

nels: the gradient and the classiﬁcation or testing ker-

nel.

Algorithm 1: Discrete Adaboost testing algorithm.

1: Given a test sample x

2: F(x) = 0

3: Repeat for m = 1, 2, .., M:

(a) F(x) = F(x) + c

· x

< P

· T

);

4: Output sign(F(x))

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

216

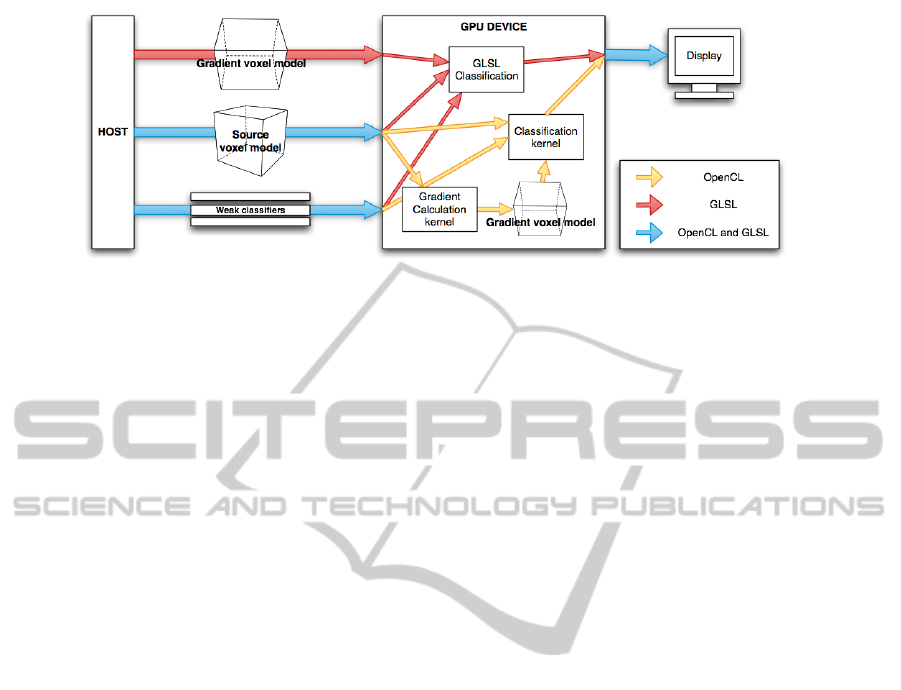
Figure 1: GPGPU implementation overview: GLSL and OpenCL approaches.

Next, we overview our proposed OpenCL classi-

ﬁcation kernel algorithm. The eight features consid-

ered for each sample by our binary classiﬁer are: the

spatial location (x, y,z), the sampled value (v), and its

associated gradient value and magnitude (gx, gy, gz,

|g|). Our binary classiﬁer has a total of N possible c

values, with N = 3 · M. We create a matrix of Work-

Groups (WG) that covers the x and y dimensions of

the dataset, whereas the component z is computed in a

loop. Each WG classiﬁes one voxel. Inside each WG,

we deﬁne N · 8 threads or WorkItems (WI) where N

is a multiple of two. Each WI computes a single step

with the three weights weak classiﬁers and produces

a value. These N · 8 values will be reduced at the end

of the execution. This process parallelizes the step

3 of the Discrete Adaboost testing algorithm deﬁned

in Algorithm 1. Finally, the sign of this computed

value (sign(F(x))) is used to obtain the label of the

processed voxels.

The way we are using threads and Global Memory

transfers follows what we call Work Group Sharing

(WGS), a short form of Work Group global memory

transfer sharing. Our WGS method is characterized

by:

• Counter intuitive global memory use. A work

group reads minimum global memory data and

produces the result for a single voxel. Classify-

ing different voxels allows the work group to read

at maximum global memory bandwidth. It is as to

say that several work groups share a single global

memory transaction, but in fact we are using only

one WG.

• To process n voxels we can use 240 threads se-

rializing n steps instead of using n threads seri-

alizing 240 steps each one. That gives a greater

number of threads and so forth better performance

(latency hiding) and scalability.

• Local memory gets alleviated. We store n half

voxels instead of 240 for each workgroup.

In summary, ﬁner grain parallelization, more local

memory and more registers available allow to extra

tune the code for faster execution.

4 SIMULATIONS AND RESULTS

In order to present the results, ﬁrst, we deﬁne the data,

methods, hardware platform, and validation protocol.

• Data. We used three datasets: the Thorax data

set represents a phantom human body; Foot and

Hand are CT scan of a human foot and a human

hand, respectively.

• Methods. We use a Discrete Adaboost classiﬁer

with 30 Decision Stumps and codiﬁed the testing

classiﬁer in Matlab, C++, OpenMP, GSGL, and

OpenCL codes.

• Hardware Platform. We used a Pentium Dual

Core 3.2 GHz with 3GB of RAM and equipped

with a NVIDIA Geforce 8800 GTX with 1 GB

of memory running a 64-bit Ubuntu Linux distri-

bution, a PC with a quad core Phenom2 x4 955

processor with 4GB of DDR3 memory equipped

with an NVDIA Geforce GTX470 with 1,28 GB

of memory. The viewport size is 700 × 650.

• Validation Protocol. We compute the mean ex-

ecution time from 500 code runs. For accuracy

analysis, we performed stratiﬁed ten-fold cross-

validation.

The classiﬁcation performance of the Adaboost-

GPU classiﬁer on each individual dataset is analyzed

in Table 1. We deﬁned different binary classiﬁcation

problems of different complexity for the three medi-

cal volume datasets. Last column of the table shows

the number of weak classiﬁers required by the clas-

siﬁer in order to achieve the corresponding perfor-

mance. For the different binary problems we achieve

performances between 80% and 100% of accuracy.

These performances depend on the feature space and

ADABOOST GPU-BASED CLASSIFIER FOR DIRECT VOLUME RENDERING

217

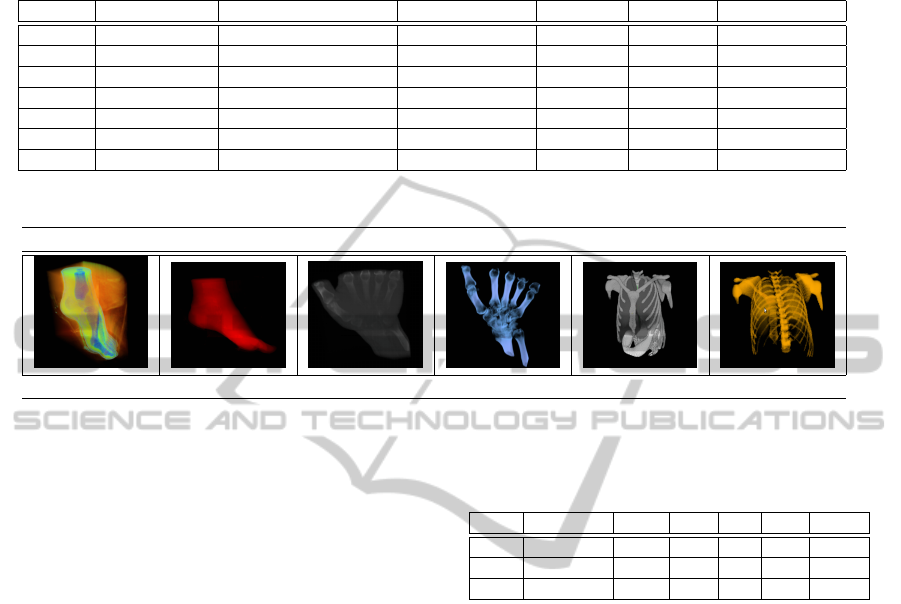
Table 1: Testing step times in seconds of the different datasets. The different labellings to learn increases the number of weak

classiﬁers needed to test them. Testing times has been obtained running our OpenCL implementation on a GTX470 graphic

card.

Dataset Size Features Weak classiﬁers Accuracy Learning Testing (GPU)

Foot 128x128x128 Bones and Soft tissue 1 99.95% 2.3s 0.0461s

Foot 128x128x128 Finger’s bone 8 99.89% 11.45s 0.1567s

Foot 128x128x128 Ankle’s muscle 7 99.21% 10.01s 0.1611s

Thorax 400x400x400 Vertebra and Column 3 99.01 3.2s 0.7157s

Thorax 400x400x400 Bone and lungs 30 84.15% 33.14s 1.9253s

Thorax 400x400x400 Bone and liver 30 78.28% 32.8s 1.9154s

Hand 244x124x257 Bone 1 100% 2.8s 0.1653s

Table 2: Results and times in seconds of the integrated OpenCL GPU-based renderings in the GTX470 graphic card.

Foot Hand Thorax

0.1256s 0.1653s 1.9253s

its inter-class variability. Binary problems which con-

tain classes with a higher variability of appearance re-

quire more weak classiﬁers in order to achieve good

performance. This increment of weak classiﬁers also

implies an additional learning time. However, the

testing time of the GSGL approach basically depends

on the size of the data set and on the number of weak

classiﬁers learned in the training stage. We can con-

clude that there also exists a constant time in the load-

ing of data into GPU, and that the variability in the

testing times is non-signiﬁcant.

In Table 2, we analyze the testing performance

for the different CPU-GPU implementations and

hardware. First of all, we have compared the time per-

formance of our GPU parallelized testing step in rela-

tion to the CPU-based implementations and the GLSL

approach. We show the averaged times of the ﬁve im-

plementations with the different sized datasets. Our

proposed OpenCL-based optimization has a speed up

of 89.91x over a C++ CPU-based algorithm and a

speed up of 8.01x over the GLSL GPU-based algo-

rithm. Finally, Table 3 shows the visualization of

the three datasets and the corresponding timings of

their visualizations, with the integrated in the render-

ing pipeline.

5 CONCLUSIONS

In this paper, we presented an alternative approach in

medical classiﬁcation that allows a new representa-

tion of the Adaboost binary classiﬁer. We also deﬁned

Table 3: Testing step times in seconds of the different

datasets with the ﬁve implementations. GLSL and OpenCL

times has been obtained using the GTX470 graphic card.

Dataset Size Matlab CPU OMP GLSL OpenCL

Foot 128x128x128 18.32s 9.63s 8s 1.32s 0.12s

Hand 244x124x257 67.29s 26s 20s. 2.86s 0.16s

Thorax 400x400x400 114.28s 33.76s 25s 4.41s 1.92s

a new GPU-based parallelized Adaboost testing stage

using a OpenCL implementation integrated to the ren-

dering pipeline. We used state-of-the-art features for

training and testing different datasets. The numerical

experiments based on large available data sets and the

performed comparisons with CPU-implementations

show promising results.

ACKNOWLEDGEMENTS

This work has been partially funded by the projects

TIN2008-02903, TIN2009-14404-C02, CON-

SOLIDER INGENIO CSD 2007-00018, by the

research centers CREB of the UPC and the IBEC

and under the grant SGR-2009-362 of the Generalitat

de Catalunya, and the CASE and Computer Science

departments of Barcelona Supercomputing Center.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

218

REFERENCES

Cerquides, J., Lpez-Snchez, M., Ontan, S., Puertas, E.,

Puig, A., Pujol, O., and Tost, D. (2006). Classiﬁca-

tion algorithms for biomedical volume datasets. LNAI

4177 Springer, pages 143–152.

Friedman, J., Hastie, T., and Tibshirani, R. (1998). Additive

logistic regression: a statistical view of boosting. In

The annals of statistics, volume 38, pages 337–374.

Micikevicius, P. (2009). 3d ﬁnite difference computation on

gpus using cuda. In General Purpose Processing on

Graphics Processing Units, GPGPU-2, pages 79–84,

New York, NY, USA. ACM.

ADABOOST GPU-BASED CLASSIFIER FOR DIRECT VOLUME RENDERING

219