BALL ROTATION DETECTION BASED

ON ARBITRARY FEATURES

Alexander Sz

Institute of Computer Technology, Vienna University of Technology, Gusshausstr. 27-29/384, A-1040 Vienna, Austria

Keywords:

Visual rotation detection, Motion tracking, Sports engineering, Racket equipment classiﬁcation.

Abstract:

This work presents an objective method to detect ball rotation in image sequences. We apply this method to

objectively classify racket sports equipment. Therefore, we observe the ball impact on a racket and compare

rotation differences detected prior to and after the impact. The method combines ball center tracking with sur-

face corner tracking to calculate ball rotation. Because our method’s application has real-time constraints our

rotation detection is fully automatic. The bottom line: Our experimental results enable racket classiﬁcations.

Athletes and sports federations are therefore our stakeholders.

1 INTRODUCTION

We present a visual method for detecting ball rotation

aimed for the ball sports domain. Knowledge about

ball rotation enables a range of applications for sports

where rotation plays a crucial role like in table tennis,

tennis, soccer, baseball, golf, bowling, and billiard.

Our envisioned application in racket sports is racket

equipment classiﬁcation. The amount of rotation a

racket imparts on a ball is a signiﬁcant classiﬁcation

factor. Such classiﬁcations can be used in two ways:

First, athletes can make objective and deliberate de-

cisions to purchase equipment. Second, sports feder-

ations can classify illegal equipment which does not

conform to the rules.

Ball rotation has been analyzed in following sports

domains: tennis (Goodwill and Haake, 2004), soc-

cer (Neilson et al., 2004), table tennis (Tamaki et al.,

2004), and baseball (Theobalt et al., 2004). Neilson et

al. (Neilson et al., 2004) measure the spin of a soccer

ball. Their results are based on a unique color pat-

tern on the ball surface where each 2D view of the

ball identiﬁes its 3D position. Our approach in con-

trast works with arbitrary corner features on a ball’s

surface. Tamaki et al. (Tamaki et al., 2004) mea-

sure ball spin of table tennis balls. Their approach is

based on image registration in addition to depth infor-

mation from a manually ﬁtted 3D sphere model. The

work of Boracchi et al. (Boracchi et al., 2009) exam-

ines spin by analyzing blurred images. For the general

case of a spinning and translating ball they propose a

semi-automatic user-assisted approach. Both (Tamaki

et al., 2004) and (Boracchi et al., 2009) require man-

ual user intervention whereas our approach is fully

automatic. Theobalt et al. (Theobalt et al., 2004) de-

termine the spin of baseballs based on multi-exposure

stereo images. Their approach relies on 3D depth data

of predeﬁned tracked color markers. We instead only

use a single camera and do not need depth informa-

tion.

Our contribution is a fully automated rotation de-

tection without user intervention. The high-speed

cameras we use deliver gray scale image data. There-

fore, our method copes with arbitrary corner features

in gray scale image data. We provide detection re-

sults within less than three seconds for 20 processed

frames—this is sufﬁcient to classify a racket. Further,

our method is independent from any motion model

and works with monocular camera data. We point out

that we only detect rotation with an axis perpendicular

to the image plane.

We brieﬂy explain our data acquisition setting in

Section 2 followed by implemented method details in

Section 3. In Section 4 we discuss experimental re-

sults and revise our contribution.

2 DATA ACQUISITION

We use rotating table tennis balls as a test environ-

ment. Compared to tennis, soccer, baseball, and

golf we can reproduce and verify results with less

effort due to a simpler data acquisition setting, de-

700

Szép A..

BALL ROTATION DETECTION BASED ON ARBITRARY FEATURES.

DOI: 10.5220/0003372707000703

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 700-703

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

picted in Figure 1. We use an automatic ball feeder

(on the left in the ﬁgure) to obtain repeatable pre-

conditions. The feeder propels the balls with back-

spin (3800 ± 100 revolutions per minute (rpm)) to-

wards the rigidly mounted racket from a short dis-

tance (0.5 m)—we capture the ball before and after

impact on the racket with a high-speed camera. The

image plane is parallel to the translational ball motion

and the camera observes the ball from 2 m distance

(focal length 100 mm). We light the scene with three

1000 W ﬂoodlights to achieve enough contrast on the

ball contour and on the ball surface features for fur-

ther processing. The main light direction of all three

ﬂoodlights is positioned perpendicular to the image

plane. The frame rate is 1000 frames per second (fps),

the exposure time is

7000

s to minimize motion blur,

and the captured image sequences have a resolution of

1280 × 512 pixels (landscape). Every certiﬁed table

tennis ball has a printed logo of the manufacturer on

its surface. A single logo is an insufﬁcient feature for

our measurement approach, therefore we augment the

surface texture with additional painted artiﬁcial fea-

tures to ensure visible texture in every captured frame.

Figure 1: Data acquisition setting.

3 SPIN CALCULATION

Figure 2 depicts the detection principle with four su-

perimposed frames of a sequence—the ball moves

from left to right as in Figure 1. The ﬁrst two frames

are taken prior to the ball impact whereas the last two

frames are taken after the impact. For better visibility

a yellow dot marks a particular surface corner which

is tracked in all ﬁve frames (this yellow dot only aug-

ments Figure 2 and does not exist on the ball itself).

The rotation magnitude results from the angle the dot

has traveled between two frames within an elapsed

time. Blue dashed lines mark the ball center in each

frame and solid red lines indicate the current angle of

the tracked dot with reference to the current ball cen-

ter. We calculate rotation magnitudes (spin rates) for

the sequence between frames 13 and 19 as well as be-

tween frames 36 and 56. The lower part of the ﬁgure

sums up the interpretation and calculation: An angle

difference of 138.5

◦

within 6 frames corresponds to

Figure 2: Detection principle.

3847 rpm whereas an angle difference of 17

◦

within

20 frames corresponds to 141 rpm.

Our basic idea is the calculation of displacements

between corresponding corners in two subsequent

frames. The approach consists of the following six

steps:

Step 1: Segmenting ball from background: To do this,

we learn a background model based on frames be-

fore a ball becomes visible in the scene. During this

learning phase we observe a certain intensity range for

each image pixel. After the learning phase a pixel is

considered as foreground when this pixel’s intensity

value is outside the learned intensity range.

Step 2: Determining center position: First, we ﬁt a

bounding box around the ball contour. Second, we ﬁt

a circle into this bounding box. Figure 3 shows an

input image with a superimposed ﬁtted circle and the

ball center. This image highlights a problem: If the

ball surface is not lit uniformly, as in our case, the

contrast varies between the projected sphere contour

and the background. This hinders accurate circle ﬁt-

ting and center ﬁnding.

Figure 3: Circle ﬁtting to ball contour.

BALL ROTATION DETECTION BASED ON ARBITRARY FEATURES

701

Step 3: Identifying corners within the ball contour:

According to the criterion for “good” corners in (Shi

and Tomasi, 1994) we identify corners where both

eigenvalues of the second moment matrix are above

a certain threshold. We set the threshold to 80% of

the best found corner’s lower eigenvalue.

Step 4: Tracking identiﬁed corners: For ﬁnding cor-

respondences between found corners we apply the

pyramid version of the Lucas-Kanade optical ﬂow

algorithm (Lucas and Kanade, 1981) which allows

for larger displacements than the conventional Lucas-

Kanade approach.

Step 5: Calculating rotational displacement: Figure 4

explains the spin calculation based on vector subtrac-

tion by means of two frames (top row of ﬁgure) super-

imposed in a third frame (lower row of ﬁgure). The

solid blue crosses mark the ball center and the dashed

red crosses mark the tracked corner. The vector sub-

traction is depicted right of the superimposed frame:

The ball translation vector in blue is subtracted from

the general corner displacement vector in red. This

results to the pure rotational displacement of the cor-

ners highlighted in green.

Figure 4: Calculating rotational displacement.

Step 6: The spin magnitude is calculated with

straightforward trigonometry and requires no further

details.

4 RESULTS AND CONCLUSIONS

Obtaining ground truth data from real image se-

quences is a tedious task. Therefore, we gener-

ated synthetic image sequences where ground truth

is known. Figure 5 visualizes a snapshot of an ana-

lyzed synthetic image sequence where the simulated

spin is 3667 rpm prior to impact. Three corners of

the square-like region are automatically chosen and

tracked. The upper right image corner contains the

three computed corresponding spin values. Ideally,

all three values should be the same, the difference be-

tween them indicates inaccuracy. Seven vectors with

three different colors are visible, their end points are

marked with dots of the same color. According to Fig-

ure 4 the ball center translation is shown in blue, the

tracked corners’ general displacements are shown in

red, and the pure rotational corner displacements after

vector subtraction of the center translation are shown

in green. In this particular snapshot we obtain a mean

error of -7.7%.

Figure 5: Spin computation (synthetic image sequence).

Figure 6 shows the calculated spins of the syn-

thetic image sequence. Ground truth spin prior to

impact is 3667 rpm and after impact 417 rpm. The

values in this diagram represent average values calcu-

lated over the number of each spin value contributed

by the tracked corners—with reference to Figure 5

this is an average over three values. Of course this

simple averaging includes also outliers but we wanted

to show the mean result variation. The mean measure-

ment error prior to impact is -4.7% and after impact

-0.9%.

Figure 6: Results of synthetic image sequence.

Figure 7 depicts a snapshot of an analyzed real

image sequence where the manually measured spin

is 3750 rpm prior to impact. The mean error -20.5%

of this sequence results mainly from inexact contour

ﬁtting and thus, inexact center computation because

of non-uniform lighting especially at the ﬁrst frames.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

702

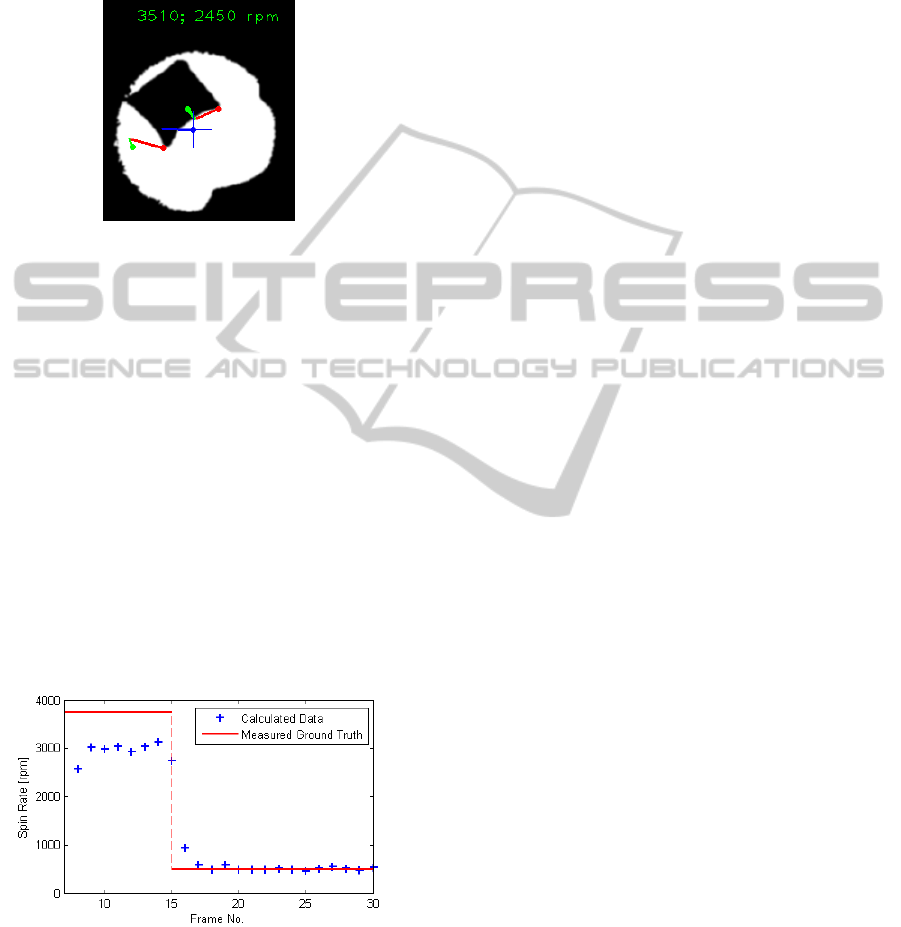
A comparison between Figure 7 and Figure 5 illus-

trates the apparently different shape of ball contours

after segmentation, additionally only two corners are

tracked in the real sequence due to corner correspon-

dence quality.

Figure 7: Spin computation (real image sequence).

Figure 8 shows the calculated spins of a real im-

age sequence. Ground truth spin prior to impact is

3750 rpm and after impact 500 rpm. Our ground truth

values are themselves error-prone as we obtain them

by manually measuring angle differences in the se-

quence on a computer display. As mentioned above

the large deviations of the values prior to impact re-

sult from inexact contour ﬁtting due to non-uniform

lighting. The mean measurement error prior to impact

is -21.8% but is simultaneously less important. Prior

to impact we can assume that the ball feeder gener-

ates a constant spin through all captured sequences—

therefore, spin prior to impact needs not to be mea-

sured accurately because no changes are expected.

In contrast, after impact, when we expect differences

caused by different rackets, the mean error magnitude

descends signiﬁcantly to 2.4%.

Figure 8: Results of real image sequence.

We captured experimental sequences with ﬁve dif-

ferent rackets according to Figure 1—overall eight se-

quences were captured, some of them with the same

racket. Manual spin measurements after impact re-

vealed an average spin range per sequence between

200 and 1250 rpm.

We have shown a motion analysis approach espe-

cially for the measurement of ball spin. Experiments

proved this method’s feasibility to infer racket prop-

erties from spin measurements based on arbitrary sur-

face features without user intervention. The execution

time for processing 20 frames was about 3 seconds (s)

(run on an Intel Core i7 L620, 2 GHz processor). A

sequence of 20 captured frames is sufﬁcient for a sig-

niﬁcant racket classiﬁcation and the time delay of 3s

is acceptable for on site classiﬁcation of illegal rack-

ets during sport events.

Future Work: We will successively challenge our

method’s robustness by decreasing the number of ar-

tiﬁcial surface features. Another measurement setting

with two opposing cameras can lower the risk of oc-

cluded features even when only a single feature is ex-

istent on the whole ball surface.

REFERENCES

Boracchi, G., Caglioti, V., and Giusti, A. (2009). Estima-

tion of 3d instantaneous motion of a ball from a single

motion-blurred image. In VISIGRAPP, pages 225–

237.

Goodwill, S. R. and Haake, S. J. (2004). Ball spin genera-

tion for oblique impacts with a tennis racket. Experi-

mental Mechanics, 44(2):195–206.

Lucas, B. D. and Kanade, T. (1981). An iterative image-

registration technique with application to stereo vi-

sion. In Proceedings of International Joint Conference

on Artiﬁcial Intelligence (IJCAI), pages 674–679.

Neilson, P., Jones, R., Kerr, D., and Sumpter, C. (2004).

An image recognition system for the measurement of

soccer ball spin characteristics. Measurement Science

and Technology, 15(11):2239–2247.

Shi, J. and Tomasi, C. (1994). Good features to track. In

1994 IEEE Conference on Computer Vision and Pat-

tern Recognition (CVPR’94), pages 593–600.

Tamaki, T., Sugino, T., and Yamamoto, M. (2004). Measur-

ing ball spin by image registration. In Proceedings of

the Tenth Korea-Japan Joint Workshop on Frontiers of

Computer Vision, pages 269–274.

Theobalt, C., Albrecht, I., Haber, J., Magnor, M., and Sei-

del, H.-P. (2004). Pitching a baseball - tracking high-

speed motion with multi-exposure images. In Pro-

ceedings of ACM SIGGRAPH.

BALL ROTATION DETECTION BASED ON ARBITRARY FEATURES

703