ILLUMINATING AND RENDERING HETEROGENEOUS

ARTICIPATING MEDIA IN REAL TIME USING

OPACITY PROPAGATION

Anthony Giroud and Venceslas Biri

University Paris Est, Marne-la-Vall´ee, LIGM, 77454 Marne-la-Vall´ee, France

Keywords:

Real-time rendering, Light scattering, Participating media, Propagation volume, Occlusion, Radial basis func-

tion.

Abstract:

We present a new approach to illuminate and render single scattering effects in heterogeneous participating

media in real time. The medium’s density is modeled as a sum of radial basis functions, and is then sampled

into a ﬁrst volumetric grid. We then integrate the extinction function from each light source to each cell in

the volume by a fast cell-to-cell propagation process on the GPU, and store the result in a second volume. We

ﬁnally render both scattering medium and surfaces using a regular step ray-marching from the observer to the

nearest surface. As we traverse the medium, we fetch data from both volumes and approximate a solution to

the scattering equation. Our method is real-time, easy to implement and to integrate in a larger pipeline.

1 INTRODUCTION

Participating media are massively used nowadays,

both in applications where real-time is required, such

the video game industry and in interactive simula-

tions, as well as in domains where visual quality is

much more important than user interactions, like cin-

ema and animation.

Figure 1: Left: the original scene. Right: a scattering media

s added.

Rendering natural phenomena such as clouds or

fog is absolutely not trivial, but is now compulsory

for any rendering engine, since these are the elements

in a scene which contribute the most to photorealism.

Considering the latest innovations and perfor-

mances of modern GPUs, it should be possible to illu-

minate and render heterogeneous fog or smoke more

easily and in real time.

Based on the three-steps algorithm and the

idea behind Light Propagation Volumes (Kaplanyan,

2009) where indirect radiance is propagated on sur-

faces, we introduce a new method to illuminate and

render in real time heterogeneous participating media

modeled as a sum of gaussians. We focus on single

scattering of light within an anisotropic medium, and

on shadow effects caused by the medium onto the ob-

jects. In this manuscript, we do not handle occlusions

by the geometry.

The contribution of this paper is:

• Establishing a modular framework to illuminate

and render inhomogenous scattering media.

• Introducing a new approach for the precomputa-

tion of the optical depth between each light source

and each point in the scene.

• Presenting an efﬁcient implementation of this

framework.

2 PREVIOUS WORK

In this section, we only focus on single scattering

techniques. For more details about global illumi-

nation techniques, the reader is invited to refer to

(Cerezo et al., 2005). Scattering media rendering

techniques are classically divided in three categories:

analytic, stochastic and deterministic methods.

We focus on deterministic methods, that seek a

113

Giroud A. and Biri V..

ILLUMINATING AND RENDERING HETEROGENEOUS PARTICIPATING MEDIA IN REAL TIME USING OPACITY PROPAGATION.

DOI: 10.5220/0003374101130118

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2011), pages 113-118

ISBN: 978-989-8425-45-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

good approximation to media rendering equations

that can allow fast computation.

(Max, 1994) and (Nishita et al., 1987) worked on

an analytic solution for rendering atmospheric scat-

tering, one of the most studied applications by re-

cent works. Later, (Stam and Fiume, 1993) applied

Nishita’s model to render turbulent wind ﬁelds. More

recently, (Biri, 2006) presented an analytic reformu-

lation of the single scattering effect of a point light

source.

Using particles to model heterogeneous participat-

ing media appears much natural, and has also already

been intensively used (Stam, 1999; Fedkiw et al.,

2001).

(Zhou et al., 2007), propose an hybrid approach

to handle single scattering in an heterogeneous par-

ticipating medium, combining particles (i.e. gaus-

sians) and spherical harmonics. Despite good perfor-

mances, since all lighting computation depend on the

observer’s point of view, the whole pipeline has to be

processed at each frame. Moreover, it seems not con-

venient to implement and not easy to integrate in an

existing pipeline.

Approaches where the medium is discretized over

a 3D grid of voxels start with (Kajiya and Von Herzen,

1984). The scattering media is modeled as a set of

voxels of varying density. As a ﬁrst step, the radiance

arriving at each voxel from each light source is com-

puted ; then, the main scattering integral is evaluated

iteratively between the viewer and the farthest voxel

intersected by a ray-tracing. Our method is inspired

from this two-step scheme.

(Kniss et al., 2003) present a technique to illu-

minate volumetric data based on half angle slicing

(Wilson et al., 1994), handling both a direct and an

approximated indirect lighting, but only for a single

light source situated outside the medium.

(Magnor et al., 2005) introduce a method to vi-

sualize reﬂection nebulae in interactive time. The

method uses a three-step algorithm similar to our

method, but where the medium’s density is kept un-

changed, due to the need for lighting precomputa-

tions.

Recently, (Kaplanyan, 2009) introduces the con-

cept of Light Propagation Volumes, to scatter indirect

lighting. After generating reﬂective shadow maps and

obtaining a set of virtual point lights on reﬂective sur-

faces, direct lighting is injected in a radiance volume,

which is a simple volumetric grid. In a third step,

using graphics hardware, indirect lighting is propa-

gated from cell-to-cell by iteratively solving differen-

tial schemes inside the volumetric grid.

Although focusing only on indirect lighting on

surfaces, this approach by propagation within a vol-

umetric grid is fast, allow more ﬂexibility and could

as well be adapted in the case of direct incoming ra-

diance within a scattering media.

3 THEORETICAL BACKGROUND

3.1 Modeling the Participating Media

using a Radial Function Basis

Because our participating media is not static and can

evolve over time, the modeling step must be as simple

as possible for the user.

Like (Zhou et al., 2007), we choose to model our

heterogeneous participating media as a sum of radial

basis functions (RBF).

To deﬁne the medium’s appearance, the user just

provides a list of radial particles, which can differ in

both amplitude and scale. The particle’s density will

then be evaluated and injected into a 3D grid.

As the radial function itself, we simply chose the

gaussian function, deﬁned on R

β(x) = ce

−a

kx−bk

(1)

where a ∈ R is its amplitude, b ∈ R

its center and

c ∈ R its scale.

To evaluate a function deﬁned in a radial function

basis, we must sum all basis functions that overlay at

the given coordinates.

f(x) =

∑

i=0

(x) ⇐

⇒ f(x) =

∑

i=0

−a

kx−b

(2)

where i is the index of the RBF, and N is the total

number of RBFs in the basis.

3.2 Our Illumination Model

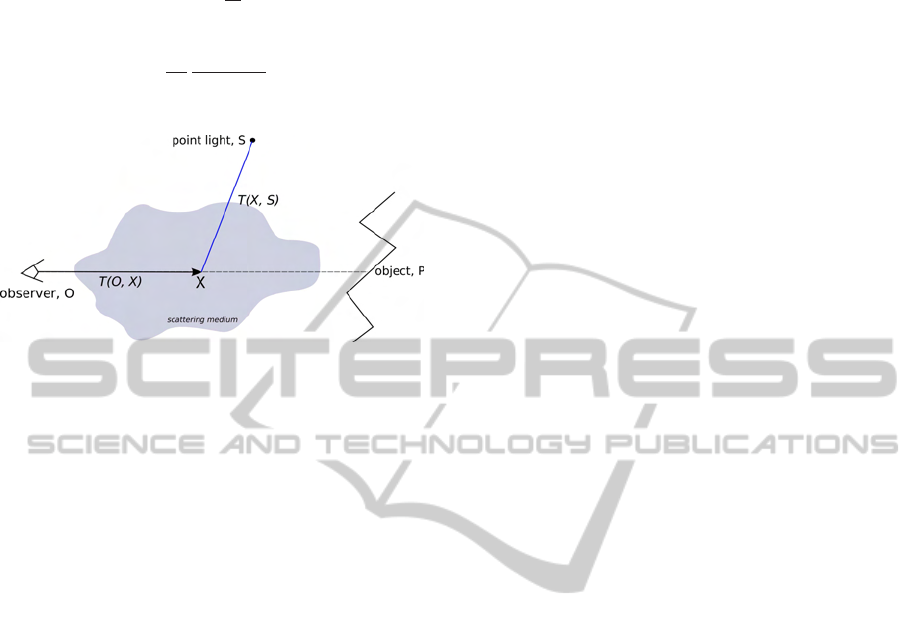
The appearance of a participating medium is linked

to airlight (Arvo, 1993). When light is emitted from a

point light source S, then goes through a participating

medium which an extinction function f (see ﬁgure 2),

the light L

(O) received by the observer at position O,

who looks in the direction of point P is given by:

(O) =

f(X)k(α(X))

kS− Xk

−T(O,X)−T(X,S)

(3)

where k(α) is the scattering phase function, I

the in-

tensity of light S, and T(A, B) is the optical depth of

the medium between points A and B:

T(A, B) =

(t)dt (4)

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

114

where K

is the extinction function of the medium.

In our method, we will assume an isotropic scat-

tering involving k(α(X)) =

4π

Therefore, our ﬁnal model is:

(O) =

f(X)

4π

kS− Xk

−T(O,X)−T(X,S)

(5)

Figure 2: The integral of T(X, S) is computed during the

opacity propagation stage (blue path), between each light S

and each position X. The integral of T(O, X) is accumulated

at the rendering step.

4 OUR METHOD

4.1 Overview

Our pipeline is composed of three steps:

1. Density injection: The medium’s extinction func-

tion f is injected into a 3D grid, called the extinc-

tion volume (EV).

2. Opacity propagation: The optical depth T(S,X)

is integrated from each light source S to each cell

in another 3D grid called the opacity propagation

volume (OPV).

3. Volume rendering: The participating medium is

rendered, using a simple ray-marching technique,

and based on data obtained at the two previous

steps.

The following sections describe each step and de-

tail the algorithm. Our application is programmed us-

ing C++ and OpenGL, and GLSL for the shaders.

4.2 Density Injection

Since our medium is composed by a set of RBFs, the

ﬁnal extinction coefﬁcient at a given point within the

medium is obtained considering all particles that over-

lay at this point.

Thanks to the low frequency nature of the scatter-

ing medium, we can avoid such costly computation

on many points by pre-sampling the extinction coefﬁ-

cients on a 3D grid: the extinction volume.

The EV is implemented as a 3D texture, having

the same dimensions as the OPV. Each texel stores

only one decimal value, therefore a 16-bit ﬂoating

point encoding is sufﬁcient. To ﬁll the texture, we

perform a plane sweep along the Z-axis (depth). Each

plane sweep step ﬁlls one texture slice, which is

bound to a framebuffer object.

For each RBF contributing to the current slice, we

draw its bounding quad facing the camera. The RBF

is computed at each point on the quad using equation

2, evaluated in a fragment shader. Since several gaus-

sians may be overlayed on the same slice, we need to

activate additive blending.

4.3 Opacity Propagation

4.3.1 The Opacity Propagation Volume

Now that the medium’s density has been discretized

into voxels in the EV, we need to compute the optical

depth between each light source S and each EV cell X.

Contrarily to (Magnor et al., 2005), we allow both the

medium and lighting to evolve over time, and must

therefore consider repeating this step for each frame

for which these conditions have changed. To achieve

this in real time, our idea is to use the radiance gath-

ering scheme presented by (Kaplanyan, 2009) for in-

direct lighting on surfaces, and adapt it to propagate

(i.e. integrate) the optical depth between each light

source and each voxel in the EV. The resulting values

are stored in a separate grid: the opacity propagation

volume.

4.3.2 Propagation Scheme

When propagating radiance in a discrete neighbour-

ing, it is actually difﬁcult to naturally simulate the

quadratic attenuation. When, like in (Kaplanyan,

2009), only cell-to-cell propagation directions are

considered, the radiance is distributed among all

neighbours and therefore scatters too rapidly around

the source, even in scenes without occluding surfaces

or media.

Because a scattering method is not adapted to an

implementation on graphics hardware, we instead use

a gathering scheme.

As each cell gathers optical depth from its six

neighbours and accounts for its own local density, our

solution is to consider both each discrete neighbour-

to-cell incoming directions and the accurate non-

discrete light-to-cell direction.

We compute a weighted mean of incoming optical

depth from all six neighbours, where the six weights

ILLUMINATING AND RENDERING HETEROGENEOUS PARTICIPATING MEDIA IN REAL TIME USING

OPACITY PROPAGATION

115

are determined by the similarity between the accurate

lighting direction

SX and the 6-connexity cell-to-cell

incoming direction, determined by their dot product.

As the light cannot arrive from a direction op-

posed to source, optical depth incoming with a neg-

ative scalar product must be discarded.

In other words, we have:

n+1

(X,S) = K(X) +

∑

i=0

S,i

(X)T

(X −

,S)

∑

i=0

S,i

(X)

(6)

where T

(X,S) is the portion of the density received

from source S by cell X at step n,

is the incoming

density direction from the i

neighbouring cell, and

which W

S,i

is the weight in the sum, given by:

S,i

= (1− K

(X))max

SX,

i,0

(7)

Figure 3: Optical depth gathering: weighting incoming di-

rections. A: Cells already visited by the propagation wave-

front are shown in blue, S is the position of the light source

and X is the center of the cell for which the gathering pro-

cess is detailed. B: We compute the dot product between

the non-discrete lighting direction

SX and each orthogonal

cell-to-cell direction. C: Neighbours whose dot product is

negative are discarded.

4.3.3 Algorithm

Like to the EV, the OPV is stored as a 3D 16-bit ﬂoat-

ing point texture with the same dimensions. Each

texel stores one optical depth integral for each light

source, i.e. one texture is need per group of four

lights. Because using a texture for both reading and

writing in a shader is not available, the propagation

process which is implemented on the GPU requires

at least two copies of each texture. They are alterna-

tively used either for reading or writing at each new

step.

The integration originates from a single cell con-

taining the light, and advances radially like a wave-

front. By marking the visited texels using an addi-

tional texture, we can speed up the process in the

shader by discarding cells which either have already

been computed, or have not been reached yet.

To initialize a new propagation process, the two

OPV textures are cleared so that each texel starts with

zero, except for the cells which contain a light source,

which are initialized with their respectivelocal extinc-

tion coefﬁcient.

Each single propagation step involves a plane

sweep along the texture slices. The gathering algo-

rithm is implemented in a fragment shader, called on

a fullscreen quad.

Algorithm 1 shows the pseudo-code of the frag-

ment shader for the gathering process.

Algorithm 1: Propagation - Pixel shader (GPU).

K(X) = Read local density from EV

for light source S do

/* 1. Gather density from neighbours */

wghtd dens sum = 0

weights sum = 0

for gathering direction

S,i

= max(dot(

SX,

), 0)

K(X −

) = Read neighbour density

wghtd dens sum += W

S,i

∗ K(X −

)

weights sum += W

S,i

end for

/* 2. Result for light S */

pxl

channels[S] = K(X) + wghtd dens sum /

weights sum

pixel color = pxl channels

end for

4.4 Rendering

4.4.1 Visualizing the Medium

Visualizing our participating medium means solving

the scattering equation 5, which deﬁnes how to obtain

the ﬁnal color of each pixel.

Considering our model, we need to perform an in-

tegration along the view ray

OP. We have little choice

but solving this integration using a conventional ray-

marching over our grid.

We use a ﬁxed integration step, even if more so-

phisticated techniques can be used (Giroud and Biri,

2010).

The entire algorithm is implemented on a frag-

ment shader, and is repeated separately for each light

source. We start the integration from the observer and

move in the direction of the surface in front of the

camera.

Based on precomputations performed in the two

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

116

previous sections, and considering equation 5, each

ray-marching step is straightforward:

1. Fetch f (X), the extinction coefﬁcient correspond-

ing to the local density of our scattering medium,

and accumulate it with the values fetched at previ-

ous steps. At this point, the density of the medium

will decide how much light will locally not pass

through and thus be reﬂected, making the medium

visible to the camera.

2. Fetch T(X, S), the optical depth between X and

each separate light source S. The radiance from S

reaching X is obtained with: e

−T(X,S)

3. Compute quadratic attenuation: kS− Xk

−2

4. Compute this step’s contribution, and add the ra-

diance in the integral result:

(X) = (1− K

(X))L

(X) + K

(X) (8)

where L

(X) is the incoming radiance from the

source, given by:

(X) = I

∗ e

−T(X,S)

(9)

5. Repeat until the nearest surface is reached.

4.4.2 Rendering Surfaces

Last but not least, in order to render the surface in

front of the current pixel, we have to use a simple

and fast illumination model. In our implementation,

we compute a simple Phong illumination, but other

models can be used as well.

The ﬁnal pixel color is ﬁnally obtained as the re-

sult of an additional integration step, outside the main

ray-marching loop:

(O) = Ph

(P, O)e

−T(O,P)−T(P,S)

kS− Xk

−2

(10)

where Ph

(P, O) is the Phong illumination for light

S, at position P on the surface, and as perceived by

observer O.

5 RESULTS

This algorithm has been implemented using GLSL,

an Intel Core 2 Quad 2.8Ghz processor and a NVidia

GeForce GTX 280 graphics card. Screen resolution is

800x600.

Although classic ray-tracing based methods have to

perform again the major part of the computations at

each frame, our pipeline is very modular.

Which computation phases are or are not per-

formed at each new frame (see table 1) is the parame-

ter which impacts most on the speed at runtime.

Table 1: Depending on the type of scene, our method makes

it possible to precompute (P) the EV density injection and

the OPV propagation, and only update (U) volumes when

required.

Static elements Injection Propagation

Nothing U U

Medium P U

Lighting and medium P P

Table 2: FPS results with different volume resolutions and

lighting conditions. (P): phases 1 and 2 are precomputed.

Volumes size 1L(P) 1L 2L 4L 8L

320 62 62 51 34

251 38 37 35 22

203 17 17 16 9

120 9 9 9 5

In table 2, we can see that computing lighting for

between one and up to four sources does not bring

signiﬁcant extra cost. With more than four lights, a

second OPV texture is required, which implies more

texture fetching and writing operations. In the second

column, only the rendering phase is performed.

Table 3: FPS results rendering mediums with different com-

plexities, with dynamic and static scenes, using extinction

and occlusion volumes with a 20

resolution, in our Cornell

box.

Nb RBFs Dynamic sc. Static sc.

1 38 251

125 36 250

1000 35 252

8000 22 215

27000 9 142

Table 3 shows that the medium’s dimensions al-

most only affect the density injection phase. After

phase 1, the complexity of the medium does not de-

pend on the number of particles anymore, but on the

number of cells in the extinction volume.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we presented a new method for illumi-

nating and rendering heterogeneous isotropic scatter-

ing media in real time. The medium is modeled by

providing a simple list of gaussians, which are ﬁrst

sampled over a volumetric grid. Then, the optical

depth T(X, S) between each light source and each grid

cell is computed by propagating occlusions through-

out a second volume using a modiﬁed version of Cry-

ILLUMINATING AND RENDERING HETEROGENEOUS PARTICIPATING MEDIA IN REAL TIME USING

OPACITY PROPAGATION

117

Figure 4: Left: Single large particle, one light. Middle: 16 particles, two lights. Right: Multiple lights in a thick fog.

tek’s algorithm. We ﬁnally render the medium and

surfaces by performing a ray-marching between the

camera and the nearest surface.

Our method fully achieves real time on conven-

tional hardware, and renders scattering effects such

as halos around light sources within the medium with

good quality. Using OpenGL and GLSL, we believe

that it is easy to implement and most of all, easy to

integrate in an existing graphics engine.

We are currently working at several improvements

to our method. First, by taking in account occlusions

by the geometry. Then, by optimizing the propaga-

tion algorithm so that the shader only processes cells

sutuated on the propagation wavefront. Finally, we

would like to speed-up our ray-marching, by optimiz-

ing GPU memory cache management.

REFERENCES

Arvo, J. (1993). Transfer equations in global illumination.

In Global Illumination, SIGGRAPH 93 Course Notes.

Biri, V. (2006). Real Time Single Scattering Effects. In Best

Paper of 9th International Conference on Computer

Games (CGAMES’06), pages 175 – 182.

Cerezo, E., Perez-Cazorla, F., Pueyo, X., Seron, F., and Sil-

lion, F. (2005). A survey on participating media ren-

dering techniques. the Visual Computer.

Fedkiw, R., Stam, J., and Jensen, H. W. (2001). Visual Sim-

ulation of Smoke. In proceedings of SIGGRAPH’01,

Computer Graphics, pages 15–22.

Giroud, A. and Biri, V. (2010). Modeling and Render-

ing Heterogeneous Fog in Real-Time Using B-Spline

Wavelets. In WSCG 2010.

Kajiya, T. and Von Herzen, B. P. (1984). Ray Tracing Vol-

ume Densities. In Computer Graphics (ACM SIG-

GRAPH ’84 Proceedings).

Kaplanyan, A. (2009). Advances in Real-Time Rendering

in 3D Graphics and Games Course. In SIGGRAPH

2009.

Kniss, J., Premoˇze, S., Hansen, C., Shirley, P., and McPher-

son, A. (2003). A model for volume lighting and mod-

eling. IEEE Transactions on Visualization and Com-

puter Graphics.

Magnor, M. A., Hildebrand, K., Lintu, A., and Hanson, A.J.

(2005). Reﬂection nebula visualization. IEEE Visual-

ization 2005.

Max, N. L. (1994). Efﬁcient Light Propagation for Multiple

Anisotropic Volume Scattering. In proceedings of 5th

Eurographics Workshop on Rendering, pages 87–104.

Nishita, T., Miyawaki, Y., and Nakamae, E. (1987). A

Shading Model for Atmospheric Scattering consider-

ing Luminous Distribution of Light Sources. In pro-

ceedings of SIGGRAPH’87, Computer Graphics, vol-

ume 21(4), pages 303–310.

Stam, J. (1999). Stable Fluids. In proceedings of SIG-

GRAPH’99, Computer Graphics, pages 121–128.

Stam, J. and Fiume, E. (1993). Turbulent Wind Fields

For Gaseous Phenomena. In proceedings of SIG-

GRAPH’93, Computer Graphics, pages 369–376.

Wilson, O., Gelder, A. V., and Wilhelms, J. (1994). Direct

volume rendering via 3d textures. Tech. Rep. UCSC-

CRL-94-19.

Zhou, K., Hou, Q., Gong, M., Snyder, J., Guo, B., and

Shum, H.-Y. (2007). Fogshop: Real-time design and

rendering of inhomogeneous, single-scattering media.

In PG ’07: Proceedings of the 15th Paciﬁc Confer-

ence on Computer Graphics and Applications, pages

116–125. IEEE Computer Society.

GRAPP 2011 - International Conference on Computer Graphics Theory and Applications

118