SCALABLE OPTICAL TRACKING

A Practical Low-cost Solution for Large Virtual Environments

Steven Maesen and Philippe Bekaert

Hasselt University - tUL - IBBT, Expertise Centre for Digital Media, Wetenschapspark 2, 3590 Diepenbeek, Belgium

Keywords:

Optical tracking, Wide-area, Low-cost, Scalable.

Abstract:

Navigation in large virtual reality applications is often done by unnatural input devices like keyboard, mouse,

gamepad and similar devices. A more natural approach would be letting the user walk through the virtual

world as if it was a physical place. This involves tracking the position and orientation of the participant over

a large area. We propose a pure optical tracking system that only uses off-the-shelf components like cameras

and LED ropes. The construction of the scene doesn’t require any off-line calibration or difﬁcult positioning,

which makes it easy to build and indeﬁnitely scalable in both size and users.

The proposed algorithms have been implemented and tested in a virtual and a room-sized lab set-up. The ﬁrst

results from our tracker are promising and can compete with many (expensive) commercial trackers.

1 INTRODUCTION

A big step towards the immersive feeling in virtual

reality is the ability to walk through the virtual en-

vironment instead of pushing buttons to move. This

requires a wide-area tracking system. But many com-

mercial systems (acoustic, mechanic, magnetic,...)

don’t support this kind of scalability.

An example of such a system is the optical track-

ing system HiBall (Welch et al., 2001), which pro-

vides great speed and accuracy. The HiBall tracker

uses a special-purpose optical sensor and active infra-

red LEDs. Their use of specially designed hardware

probably explains why the system is so expensive.

Our main goal is to build a pure optical wide-area

tracking system at a low cost using only off-the-shelf

components. We also don’t expect the position of

each LED to be known or calibrated, which makes the

construction of the set-up fast and easy. By using only

passive markers, we can support an indeﬁnite number

of cameras to be tracked because there is no synchro-

nization required between them and each camera is a

self-tracker (Bishop, 1984). It also makes it very easy

to expand the working volume indeﬁnitely provided

you have sufﬁcient ceiling space.

2 RELATED WORK

Tracking of participating persons has been a funda-

mental problem in virtual immersive reality from the

very beginning (Sutherland, 1968). In most cases,

special-purpose hardware trackers were developed

with usually a small (accurate) working area. Most

trackers are used to track the head of a person wearing

a head mounted display (HMD) to generate the virtual

world from their point of view. Many different tech-

nologies have been used to track HMDs: mechanical,

magnetic, acoustic, inertial, optical, ... and different

kinds of hybrid combinations.

The ﬁrst HMD by Ivan Sutherland (Sutherland,

1968) used a mechanical linkage to measure the head

position. Mechanical trackers are very fast and accu-

rate, but suffer from a limited range because the user

is physically attached to a ﬁxed point.

Magnetic-based systems on the other hand don’t

have a physical linkage with the magnetic source, in

fact they don’t even need a line-of-sight between its

source and receiver. But they suffer from a limited

range (as do all source-receiver systems that use only

1 source) and are not very scalable. Also metal or

other electromagnetic ﬁelds cause distortions in the

pose measurements.

Acoustic tracking systems use ultrasonic sounds to

triangulate its position. This system does require a

line-of-sight between source and receiver and also

suffers from a limited range. The accuracy of the sys-

tem also depends on the ambient air conditions.

Inertial tracking systems use inertia to sense po-

sition and orientation changes by measuring accel-

538

Maesen S. and Bekaert P..

SCALABLE OPTICAL TRACKING - A Practical Low-cost Solution for Large Virtual Environments.

DOI: 10.5220/0003374205380545

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 538-545

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

eration and torque. This type of system doesn’t re-

quire any source or markings in the environment and

therefore has an unlimited range. However this also

means that there is no absolute position given and the

measured position quickly drifts from the exact posi-

tion. Inertial self-trackers are often combined with vi-

sion systems (optical trackers) to counteract the weak

points of each other. An example of such a hy-

brid tracker is the VIS-Tracker (Foxlin and Naimark,

2003; Wormell et al., 2007). The VIS-Tracker uses

paper patterns for absolute reference to counter drift

from its inertial tracker. Filming paper markings has

the disadvantage of needing enough light and a long

shutter time, which increases the effect of motion blur.

The patterns also need to be calibrated before use.

With the rapid rise of CPU speeds and advances

in affordable camera systems, computer vision based

tracking systems can operate in real-time. But the best

vision based systems, like the HiBall tracker (Welch

et al., 2001), still are very expensive and require spe-

cial hardware. Optical systems need line-of-sight to

detect feature points in the world, but can have a great

accuracy and update rate with hardly any latency as

shown by the commercially available HiBall tracker.

Another low-cost optical tracking system was de-

veloped at MERL (Raskar et al., 2007) which esti-

mates position, orientation and incident illumination

at 124 Hz. They use cheap electronic components to

build a projector of light patterns. The receiver uses

these coded light signals to estimate position and ori-

entation. But the system only has a limited working

area of a few meters.

More information about all these techniques

can be found in the course ”Tracking: Beyond 15

Minutes of Thought” by Gary Bishop, Greg Welch

and B. Danette Allen (Allen et al., 2001).

Our goal is to make a wide-area tracking system

that allows the user to walk around in a building. Most

systems discussed above only have a limited range

and therefore aren’t really suited for this task. The

VIS-Tracker and the HiBall tracker are designed for

the same goal. But the VIS-Tracker mostly relies on

its inertial tracker and uses its camera secondary for

recalibration of its absolute position. The HiBall on

the other hand is also a pure optical tracking system.

In fact their set-up shows similarities in the way that

we also chose a inside-looking-out system with mark-

ers on the ceiling.

The HiBall system uses a specially designed sen-

sor with multiple photo diodes that measures the

position of each sequentially ﬂashed infra-red LED

in the specially designed ceiling. The system uses

the 2D-3D correspondences of each LED to accu-

rately estimate the position and orientation of the Hi-

Ball as discussed by Wang (Wang et al., 1990) and

Ward (Ward et al., 1992). The ﬁnal version of the

HiBall tracker uses a single-constraint-at-a-time ap-

proach or SCAAT tracking (Welch, 1997).

We take a different approach to estimate rota-

tion and position. We calculate the orientation from

the vanishing points of the constructed lines paral-

lel to the X- and Y-directions. This can be done

separately from the cameras position. Camera cali-

bration from vanishing points isn’t a new technique.

Caprile (Caprile and Torre, 1990) used vanishing

points for off-line calibration of a stereo pair of cam-

eras. Cipolla (Cipolla et al., 1999) used a similar tech-

nique to calibrate images of architectural scenes for

reconstruction purposes.

3 OVERVIEW TRACKING

SYSTEM

3.1 Set-up of the Tracking System

In our set-up, we have constructed a grid of LED

ropes to identify the parallel lines in both the X and

Y direction on the ceiling. We consider the distance

between LED ropes to be known which is needed for

position tracking.

The person or object that needs to be tracked will

have a camera placed on top of it pointing upwards.

We will consider the intrinsic parameters of the cam-

era known. Those values are constant if we assume

that the camera does not have a variable zoom or fo-

cus.

We choose to use LED ropes instead of ordinary

markers because it makes the construction and detec-

tion in a real lab set-up easier. Choosing a LED rope

saves a lot of time because we don’t need to attach

each LED separately and minimal extra wiring is re-

quired. Mass production of LED ropes also reduces

production costs, which makes them relatively cheap.

By using light sources instead of markers, we can de-

crease the shutter time of our cameras. This means we

can have a higher camera frame rate, less background

noise and motion blur in our images. This increases

the performance and robustness of our tracking sys-

tem.

Figure 1 shows our lab set-up tracking one person

with virtual reality glasses by ﬁlming the grid of LED

ropes on the ceiling.

SCALABLE OPTICAL TRACKING - A Practical Low-cost Solution for Large Virtual Environments

539

Figure 1: Our lab set-up with a 4 by 3 meter grid of LED ropes on the ceiling. The camera mounted on the virtual reality

glasses tracks its position and orientation by ﬁlming this grid.

3.2 Overview Algorithm

Our tracking algorithm gets the images of the camera

as input. The extrinsic parameters will be estimated

in the following steps:

• Detection of the LED ropes

• Calculating orientation from vanishing points

• Calculating position with known orientation

These steps will be explained in detail in the following

sections.

4 DETECTION OF THE LED

ROPES

Our ﬁrst task is the detection of our constructed grid

in the input image. We ﬁrst segment the individual

LEDs by evaluating the hue value of each pixel. Then

we use a simple ’ﬂood ﬁll’ algorithm to cluster the

pixels corresponding to a LED and retain only its cen-

ter. That way we speed up the line detection consid-

erably and eliminate a lot of random noise.

Secondly if we use a real camera, we need to take

lens distortion into account. The effects of lens dis-

tortion are clearly visible when using a lens with a

wide ﬁeld of view. It causes straight lines to bend,

especially near the edges. This is something we want

to avoid at all costs. Therefore we calculate the dis-

tortion parameters beforehand with ’GML Toolbox’

(V.VezhnevetsandA.Velizhev, 2005) based on the im-

age processing library OpenCV (Bradski, 2000). Un-

like the undistortion function in OpenCV, we do not

want to undistort entire images because that would be

prohibitory slow. Instead we create a lookup table to

undistort individual LEDs very fast.

Last step in the detection of the LED ropes is the

line pattern recognition in the collection of detected

LEDs. A mature technique for line pattern recogni-

tion is the patented Hough Transform (Hough, 1962).

4.1 Hough Transformation

In general the Hough transformation is a mapping

of the input points to a curve in a dual parameter

space. The parameterization of the pattern (in this

case a line) determines the used parameter space and

the shape of the dual curves. The most common used

parameterization maps an input point (x

) to a si-

nusoidal curve in the ρθ-plane with equation:

cosθ+ y

sinθ = ρ (1)

The geometrical interpretation of the parameters

(θ,ρ) is illustrated in ﬁgure 2.

Figure 2: Left: Geometrical interpretation of the (θ, ρ) pa-

rameterization of lines. Right: Subdividing the parameter

space into accumulator cells. (Image courtesy: (Gonzalez

and Woods, 2001)).

The Hough algorithm (Gonzalez and Woods,

2001) attains its computational attractiveness (O(N))

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

540

by subdividing the parameter space into so-called ac-

cumulator cells (Figure 2). Each input point gener-

ates votes for every accumulator cell correspondingto

its mapped sinusoid in parameter space. Finally the

accumulator cells with the highest amount of votes

(most intersections) represent the line patterns in the

input space.

Although the Hough algorithm has a linear time

complexity, it has a high constant cost of ’drawing’

and searching for ’highlights’. Therefore most Hough

transformations cannot be performed in real-time. Al-

though we only have a small number of input points,

the high constant cost weighed heavily on the trackers

speed. Therefore we propose another line parameter-

ization to speed up the calculations with a relatively

small amount of input points.

4.2 Line Parameterization with Circles

To increase the speed and accuracy of the line de-

tection, we propose to calculate the intersections in

the Hough parameter space analytical. But this isn’t

trivial with sinusoidal curves (eq. 1). Therefore we

propose a new parameterization that maps each input

point (x

) to a circle in the XY-plane with equation:



x−





y−



−C

)

+ (y

−C

)

(2)

with (C

) a ﬁxed point in the image, like the prin-

cipal point. This means that for every point (x

)

we will construct a circle with the midpoint between

) and (C

) as center and radius equal to half

the distance between these two points. The geometri-

cal interpretation of this parameterization is shown in

Figure 3.

The analytic intersection point of 2 circles is much

easier to calculate than with 2 sinusoids. Given 2 cir-

cles with centers C

and C

and radiuses r

and r

and

the ﬁxed point C, we can calculate the second inter-

section point P (ﬁrst intersection point is C) as fol-

lows:

P = (C

) +

− r

−C

) −C

with d the distance between C

and C

In practice, we will represent each line with this in-

tersection point P. This ’line center’ deﬁnes a line

through this center P and perpendicular to the direc-

tion

PC.

Figure 3: Geometrical interpretation of the circle parame-

terization of lines. Each line L through input point (x

) is

characterized by a point (x,y) ∈ C.

4.3 Line Detection with the New

Parameterization

To detect lines in our input image, we try to esti-

mate the most apparent line centers. For every LED

in the input image, we try to estimate a local direc-

tion/line, e.g. by using the closest LED. Each of these

lines deﬁnes a line center in the line parameterization

space. Noise and measurement errors cause the lo-

cal line centers representing the same line to slightly

vary their position. This means that we must deﬁne a

dynamic error bin around possible groups of line cen-

ters. The bins with the most points represent the most

apparent line patterns in the image. The algorithm has

an average complexity of O(N

). In applications with

a small set of input points -like our tracker- our Hough

algorithm greatly outperforms the standard algorithm.

5 CALCULATING ORIENTATION

FROM VANISHING POINTS

The lines detected in the previous step are the pro-

jections of the constructed parallel lines. Therefore

we know that each set of lines corresponding to one

axis (one color of LEDs) intersects in a single point,

the vanishing point. Classically the best ﬁt intersec-

tion point of the lines is used as the vanishing point.

This can introduce a lot of jitter in the vanishing

point when the lines are nearly parallel. Therefore

we propose to calculate the vanishing direction sep-

arate from the distance to the vanishing point. The

vanishing direction is the direction from the principal

point of the camera to the 2D position of the vanish-

ing point. If we used the principal point as the ﬁxed

point in the line detection step (§4.2), it can be shown

SCALABLE OPTICAL TRACKING - A Practical Low-cost Solution for Large Virtual Environments

541

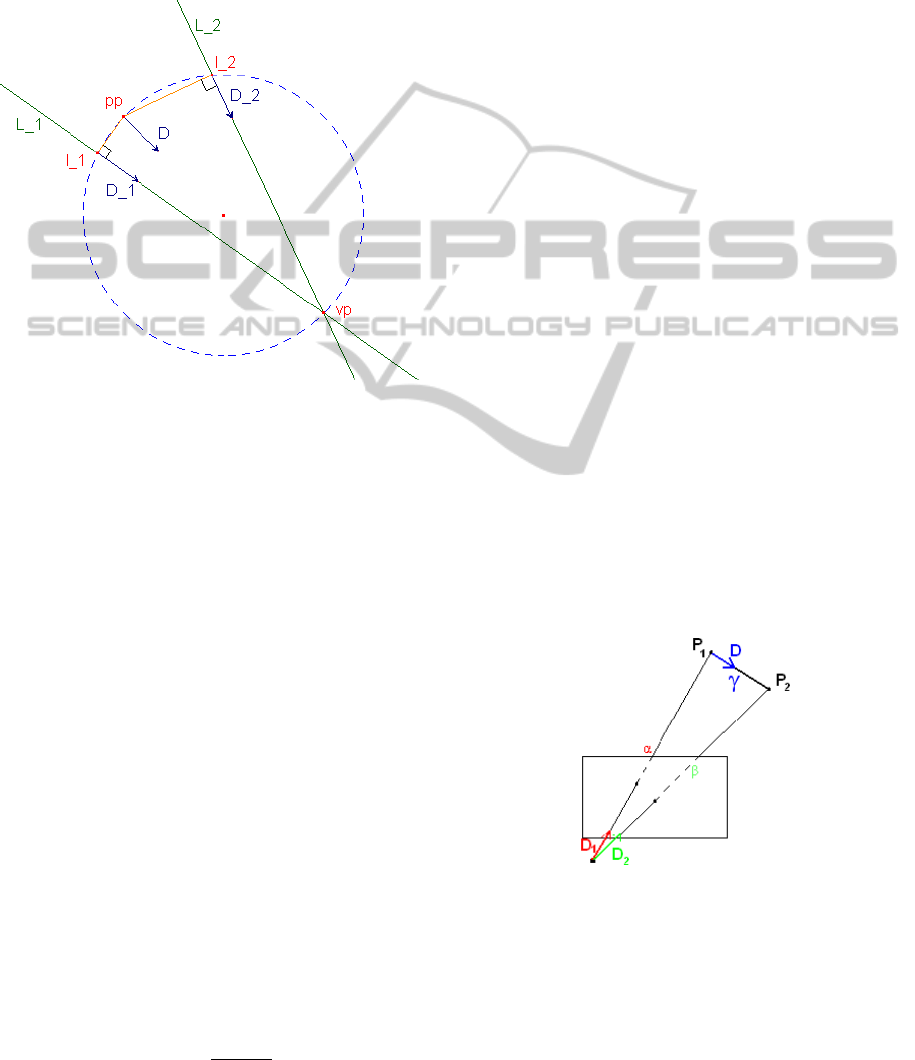
that the vanishing direction D equals the interpolation

of two line directions D

and D

D = ||l

, pp|| ∗ D

+ ||l

, pp|| ∗ D

(3)

with pp the principal point and l

, l

the line cen-

ters from lines L

and L

. Figure 4 gives a geomet-

ric representation of the interpolation. The vanishing

Figure 4: Calculating the vanishing direction D separate

from vanishing distance. The ﬁxed point in this parameteri-

zation is the principal point pp. vp is the vanishing point of

lines L

and L

, with l

and l

as their line centers and D

and D

their line directions.

point corresponds with a point at inﬁnity (intersec-

tion of parallel lines) and therefore is unaffected by

translation. This means that we can calculate the ro-

tation independent from the translation (Caprile and

Torre, 1990; Cipolla et al., 1999). We can see this

clearly in the projection equation of the vanishing

point V

= (u

), the projection of the point at in-

ﬁnity D

= (x

D,i

,0) (direction of the parallel

lines):









= K[R|T]







D,i







(4)

with λ

a scale factor, K the calibration matrix with

the intrinsic parameters, R the rotation matrix and T

the translation vector. Which gives us:

−1

= RD

(5)

The only unknown factor λ

can be calculated using

the fact that the inverse of a rotation matrix is its trans-

pose (so R

R = I) (Foley et al., 1996) and D

is a

normalized direction vector (so D

= 1):

= ±

−1

(6)

By using the coordinates of the found vanish-

ing points with their corresponding directions (X-,Y-

,Z-axis), the rotation matrix can be calculated from

Equation 5. Because of the uncertainties of the sign

of λ

, the orientation is ambiguous but this can be

solved by looking at previous frames or adding an ex-

tra marker.

The calculation of the 9 unknowns of the 3x3 ro-

tation matrix seems to require 3 vanishing points. But

knowing that the 3 rows of the matrix form an orthog-

onal base (Foley et al., 1996), we only need 2 corre-

spondences and therefore only 2 axis must be visible

at all times (in our case the X- and Y-axis, the ceiling).

6 CALCULATING POSITION

WITH KNOWN ORIENTATION

Given the rotation matrix and point or line correspon-

dences between frames, the direction of the transla-

tion can be recovered (Caprile and Torre, 1990). The

length of the translation is impossible to determine

without a reference distance in the input image. In

our system we choose to use the known interdistance

between LED ropes.

Caprile (Caprile and Torre, 1990) demonstrates

that by using 2 image points (with camera directions

and

) and known length γ and orientation

D be-

tween the world coordinates of points P

and P

, we

can calculate the distances to both points (α and β) by

triangulation (see Figure 5). Thus we have the follow-

ing system of linear equations with unknowns α and

β:

D = β

− α

(7)

Figure 5: Depth estimation (α,β) of two points P

and P

can be done by a simple triangulation given the distance γ

and spatial orientation

D of the chosen points.

Given the rotation matrix calculated in the previ-

ous step, we undo the rotation on the lines. What we

get is a regular grid parallel to the image plane. Since

we know the distance between two neighboring lines,

the absolute distance to the ceiling can be calculated

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

542

by using triangulation (Equation 7). It is also not re-

quired that the X- and Y-lines are at the same height, if

the distance between them is known. This fact makes

the construction of our lab set-up easier.

The only remaining unknown is the translation in

X- and Y- direction. Given the lines in the previous

frame, this translation can be trivially calculated.

7 RESULTS

The proposed algorithms have been implemented and

tested in a virtual set-up as well as in a real room-sized

lab set-up.

7.1 Virtual Set-up

To evaluate the soundness of our algorithm and de-

sign, we ﬁrst constructed a virtual scene (see Figure

6). The virtual scene consists of a 8 by 10 meters

room and about 2.5 meters in height. The ceiling of

this room consists of a 2D grid of markers (LEDs) in

2 colors: red LEDs to indicate the lines parallel to the

X-axis and green to indicate those parallel to the Z-

axis. The distance between 2 adjacent parallel lines is

known, namely 50 cm.

Figure 6: Implementation of the virtual set-up. Left: view-

point of the user. Right: viewpoint of the tracker camera

and input of the tracking system.

A virtual test set-up has the advantage of knowing

the exact position and orientation of the user. We use

this data to evaluate our tracking system. The test con-

sists of a path through the virtual environment while

looking around. The run has been performed on a

standard pc and consists of about 400 frames at a res-

olution of 1024x768.

Figure 7(a) shows the calculated look- and up-

vectors deﬁning the orientation of the camera poses

of the run. Because we have the real orientation of the

camera, we can calculate the absolute RMS error. We

ﬁnd that the accuracy of our algorithm on relatively

noise free data is about 0.02

◦

for Yaw and 0.035

◦

for

Pitch and Roll.

Using this rotation, the path traveled by the cam-

era can be calculated (Figure 7(b)). We compare the

calculated positions with the real poses and get a RMS

accuracy of 4 millimeter in X- and Y-directions and

2.4 millimeter accuracy of the height of the camera.

Both orientation and position give a good result

under near optimal conditions. Therefore we built a

real set-up to test this under real-world conditions.

7.2 Lab Set-up

A virtual set-up is good to do the initial testing, but

our goal is off course to build a real tracking sys-

tem. So we constructed a room-sized (4x3 meter)

lab set-up as visible on Figure 1. Figure 9 shows

a input image of the camera that we want to track.

We use a ’Point Grey Flea Firewire’ camera captur-

ing 1024x768 images at 30 fps with a wide ﬁeld of

view camera. Because we use LEDs, the shutter time

can be set at as little as 1 ms, which practically elim-

inates motion blur. This also implies that the system

can work in a large variety of lighting conditions, as

long as the LED’s are the brightest colored features.

Figure 8 shows the recording of estimated orientation

and position during a walk through our lab set-up.

Unlike the virtual set-up, we cannot compare the

results with absolute data. Therefore we captured

around 2000 frames at a stationary pose and took the

average as the ground truth position. The RMS er-

ror of the orientation tracker gives us an accuracy of

0.16

◦

Yaw and 0.23

◦

Pitch and Roll. The position

data gives us an accuracy of 5 millimeter in X- and

Y-direction and 8 millimeter in the Z-direction. If we

look at the processor time the camera tracker requires,

we see that it does not need more than 11 milliseconds

to compute. Most of this computing power (around

9.5 ms) is required to segment the LEDs, but still a lot

of processor power is left for other tasks or improve-

ments to our algorithm.

During tests, we’ve seen that the system func-

tions well under varying lighting conditions. How-

ever when used with the room lights, the LEDs under

the light can’t be segmented due to the camera’s low

dynamic range.

Although the tracking algorithm does not experi-

ence any drift, the global pose of persons using the

system can differ. Some sort of global starting posi-

tion must be deﬁned if all participants need to be in

the same world space. There is also an inherit ambi-

guity in the global pose if the user moves when the

sensor is occluded. This problem could be improved

if we use an inertial sensor when line-of-sight is bro-

ken or by placing global positioning beacons.

SCALABLE OPTICAL TRACKING - A Practical Low-cost Solution for Large Virtual Environments

543

Figure 7: Results of the orientation and position tracker on input of a virtual camera. Left (a): Position of the look vector

(green) and up vector (blue) on the unit sphere with the original orientation overlaid (red). Right (b): Position of the camera

(blue) with the original position overlaid (red).

Figure 8: Tracking results of the camera tracker in a room-sized lab set-up. Left (a): Orientation of the calculated camera

with the look vector (blue) and up vector (green) on the unit sphere. Right (b): Estimated position of the camera in the lab.

Figure 9: Image from the camera in our lab set-up.

8 CONCLUSIONS AND FUTURE

WORK

In this paper we have proposed our low-cost wide-

area optical tracking system using regular cameras

and LED ropes. Our proposed real-time orientation

tracking algorithm using vanishing points has been

shown to be accurate and fast. This could be accom-

plished using a new parameterization of the Hough

transform for detecting line patterns. We are currently

looking at iterative reﬁnement algorithms to get even

better results.

We are also looking to expand our current test set-

up to a larger theater room. This may require the

placement of global beacons to get an absolute po-

sition when line-of-sight is restored.

The ﬁrst results from our tracking system are very

promising for a build-it-yourself wide-area tracker.

With orientation accuracy under 0.25 degrees and

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

544

position errors smaller than 1 cm, our system can

compete with many expensivecommerciallyavailable

tracking systems on the market.

ACKNOWLEDGEMENTS

Part of the research at EDM is funded by the ERDF

(European Regional Development Fund) and the

Flemish government. Furthermore we would like to

thank our colleagues for their help and inspiration.

REFERENCES

Allen, B., Bishop, G., and Welch, G. (2001). Tracking:

Beyond 15 minutes of thought. In SIGGRAPH 2001,

Course 11.

Bishop, T. G. (1984). Self-tracker: a smart optical sensor

on silicon. PhD thesis, Chapel Hill, NC, USA.

Bradski, G. (2000). The OpenCV Library. In Dr. Dobbs

Journal of Software Tools.

Caprile, B. and Torre, V. (1990). Using vanishing points for

camera calibration. In Int. Journal Computer Vision.

Kluwer Academic Publishers.

Cipolla, R., Drummond, T., and Robertson, D. (1999).

Camera calibration from vanishing points in images

of architectural scenes. In BMVC ’99, British Machine

Vision Conference.

Foley, J. D., van Dam, A., Feiner, S. K., and Hughes, J. F.

(1996). Computer graphics: principles and practice

(2nd ed. in C). Addison-Wesley Longman Publishing

Co.

Foxlin, E. and Naimark, L. (2003). Vis-tracker: a wear-

able vision-inertial self-tracker. In IEEE Virtual Real-

ity 2003.

Gonzalez, R. C. and Woods, R. E. (2001). Digital Im-

age Processing. Addison-Wesley Longman Publish-

ing Co., New Jersey, 2nd edition.

Hough, P. V. C. (1962). Method and means for recognizing

complex patterns. United States Patent 3069654.

Raskar, R., Nii, H., Dedecker, B., Hashimoto, Y., Summet,

J., Moore, D., Zhao, Y., Westhues, J., Dietz, P., Barn-

well, J., Nayar, S., Inami, M., Bekaert, P., Noland, M.,

Branzoi, V., and Bruns, E. (2007). Prakash: lighting

aware motion capture using photosensing markers and

multiplexed illuminators. In SIGGRAPH ’07: ACM

SIGGRAPH 2007 papers, New York, NY, USA. ACM

Press.

Sutherland, I. E. (1968). A head-mounted three dimensional

display. In Proceedings of the 1968 Fall Joint Com-

puter Conference, AFIPS Conference Proceedings.

V.Vezhnevets and A.Velizhev (2005). Gml

c++ camera calibration toolbox.

http://research.graphicon.ru/calibration/gml-c++-

camera-calibration-toolbox.html.

Wang, J., Azuma, R., Bishop, G., Chi, V., Eyles, J., and

Fuchs, H. (1990). Tracking a head-mounted display

in a room-sized environment with head-mounted cam-

eras. In Proc. of Helmet-Mounted Displays II.

Ward, M., Azuma, R., Bennett, R., Gottschalk, S., and

Fuchs, H. (1992). A demonstrated optical tracker with

scalable work area for head-mounted display systems.

In SI3D ’92: Proceedings of the 1992 symposium on

Interactive 3D graphics. ACM Press.

Welch, G., Bishop, G., Vicci, L., Brumback, S., Keller, K.,

and Colucci, D. (2001). Highperformance wide-area

optical tracking: The hiball tracking system. In Pres-

ence: Teleoperators and Virtual Environments.

Welch, G. F. (1997). SCAAT: incremental tracking with in-

complete information. PhD thesis, Chapel Hill, NC,

USA.

Wormell, D., Foxlin, E., and Katzman, P. (2007). Advanced

inertial-optical tracking system for wide area mixed

and augmented reality systems. In EGVE 2007, 13th

Eurographics Workshop on Virtual Environments.

SCALABLE OPTICAL TRACKING - A Practical Low-cost Solution for Large Virtual Environments

545