
TWO-LEVEL STRATEGY
FOR IMAGE BOUNDARY DETECTION
Karin S. Komati, Evandro O. T. Salles and Mario Sarcinelli-Filho
Graduate Program on Electrical Engineering, UFES, Av. Fernando Ferrari, 514, Vitória/ES, Brazil
Keywords: Boundary detection, Multifractal measurement, J value, 1/f spectrum, Region-growing, Edge detection.
Abstract: A new method for boundary detection in natural images is here proposed, consisting of two levels, or two-
stage sequential processes: embedded integration and post-processing integration. In the embedded
integration, two different methods to measure homogeneity in region-growing technique are integrated,
based on a global statistical property: the shape of the power spectrum of the image being analyzed. One
homogeneity measure is the J value (provided by the classical JSEG algorithm) and the second measure is a
multifractal measurement. This first step provides a region extraction. In the second level, edge information
is extracted by a classical method, and integrated with region information. This structure, called KSS,
eliminates false boundaries in the region map, guided by the edge map, and the noise in edge map as well,
now guided by the region map, thus taking the advantage of their complementary nature. Experiments on a
large dataset of natural color images show that the result of such two-level strategy matches the human
perception better than the individual methods, quantitatively and qualitatively speaking.
1 INTRODUCTION
Boundary detection is one of the most important
tasks in computer vision. Traditionally, the
techniques can be classified in region or edge
approaches. There may exist gaps and noisy edges in
edge-approach results, whereas region-approach
results tend to be over-segmented with inaccurate
boundaries. There are many proposals combining the
outputs of region-growing and edge detection
methods to improve the quality of their results.
Muñoz, Freixenet, Cufí and Martí (2003) show
seven different strategies for combining similarity
(region) and discontinuity (edge) information. They
were grouped in two classes: embedded integration
and post-processing integration.
In this work, these two classes are considered in
two sequential levels. In the embedded integration,
the J value obtained by using the classical JSEG
method (Deng and Manjunath, 2001) and a
multifractal measurement are integrated, the
integration being controlled by the shape of the
power spectrum of the image under analysis. Such
statistical property is also used to calibrate the
threshold of the merging process. The segmentation
obtained by merging the results of both individual
methods (hereinafter referred to as MM-Frac
method) is more informative than the result of each
individual method, as it is shown ahead.
Till now, the region-growing result of MM-Frac
and edge information are extracted parallely and
separately. Our strategy is to put the two maps
together, eliminating the false boundaries in the
region map, based on edge information, and
eliminating the noisy edges in the edge map, based
on region information. Such method is hereinafter
referred to as KSS (Komati, Salles and Sarcinelli-
Filho, in press). In the sequel, we show that the
resulting image is closer to human perception than
any of the two images used as input for the post-
processing integration.
Quantitative performance comparison requires
ground truth and well defined metrics. Both
requirements can be found in “The Berkeley
Segmentation Dataset and Benchmark” (BSDS)
(Martin, Fowlkes, Tal and Malik, 2001). For each
image in the BSDS, there are at least five hand-
labeled segmentations made by human beings,
which constitute the ground truth. The standard
metrics of BSDS are precision, recall and F-
measure, determining how well the boundary map
approximates the human ground truth boundaries
(Martin, Fowlkes, and Malik, 2004).
181
Komati K., Salles E. and Sarcinelli-Filho M..
TWO-LEVEL STRATEGY FOR IMAGE BOUNDARY DETECTION .
DOI: 10.5220/0003375801810186
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 181-186
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 THE PROPOSED METHOD
2.1 First-Level of Integration
2.1.1 J value
The essence of the JSEG method is to separate the
segmentation process in two independently
processed stages: color quantization and spatial
segmentation. The result of color quantization is a
class-map which associates a color class label to
each pixel belonging to a class.
In the spatial segmentation stage, a criterion to
measure the distribution of color classes, the J
measure, is calculated. Essentially, it measures the
distances between different classes, divided by the
distances between the members within each class, an
idea similar to the Fisher's multi-class linear
discriminator. The J value can be calculated by
using a local area of the class-map. Multi-scale J-
images are calculated changing the local window
size. In the J-image, the higher the local J value is,
the more likely the pixel is part of a boundary
region, like a 3-D terrain map containing valleys and
mountains. Then, a region growing method is used
to segment the image. Finally, to overcome the over-
segmentation problem, regions are merged based on
their color similarities, by directly applying a
Euclidean distance measure.
2.1.2 The Multifractal Measurement
In this work, we will use the differential box-
counting method, proposed by Chaudhuri and Sarkar
(1995), to estimate the multifractal measurement
(MM) of the original image.
The MM of a single pixel is calculated in a small
window surrounding it, generating a Fractal-image
for each channel in Luv color space (Komati et al.,
2010). The Fractal-images are also a 3D terrain
maps, that is because the MM in the border regions
of a texture is lower than the MM of a homogeneous
region (Pentland, 1984). Each value in Fractal-image
is converted to be higher in boundary regions and to
have the same limits applied to a J-image.
2.1.3 1/f Spectra of Natural Images
Statistics of natural images have been found to
follow particular regularities. Torralba and Oliva
(2003), studying the statistics of real-world images,
observed that the energy spectra of such images
falls, in average, into a form 1/f
α
with α∼2. They
also show that the shape of the power spectrum can
be used to categorize the different semantic of
scenes (single objects, rooms, places, large outdoors
and panoramic scenes).
(a)
(b)
Figure 1: Graphic of one image power spectrum (a) 3D (b)
2D.
Here α represents the slope of the decreasing
energy spectrum values, from low to high spatial
frequencies, varying with the scene complexity.
Figure 1(a) exemplifies a 3D power spectrum, where
the slope is emphasized in red. Figure 1(b) shows
the slope (red) in a 2D graphic and the interpolated
slope (the dotted black line). The estimated -α value
is then -2.31, or α value is then +2.31.
Pentland (1984) showed that fractal natural
surfaces (as mountains, forests) produce a fractal
image with an energy spectrum of the form 1/ f
α
,
where α is related to the fractal dimension of the 3D
surface (e.g., its roughness). Slope characteristics
may be grouped in two main families, a slow slope
(α∼1), for environments with textured and detailed
objects, and a steep slope (α∼3), for scenes with
large objects and smooth edges. Thus, the slower the
slope is, the more textured the image is.
2.1.4 MM-Frac
In this new proposal, the integration of two
measurements, J-image and Fractal-image, is
controlled by the value of α as in the work of Côco,
Salles, Sarcinelli-Filho (2009). Figure 2 shows a
simplified architecture of the proposed MM-Frac
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
182
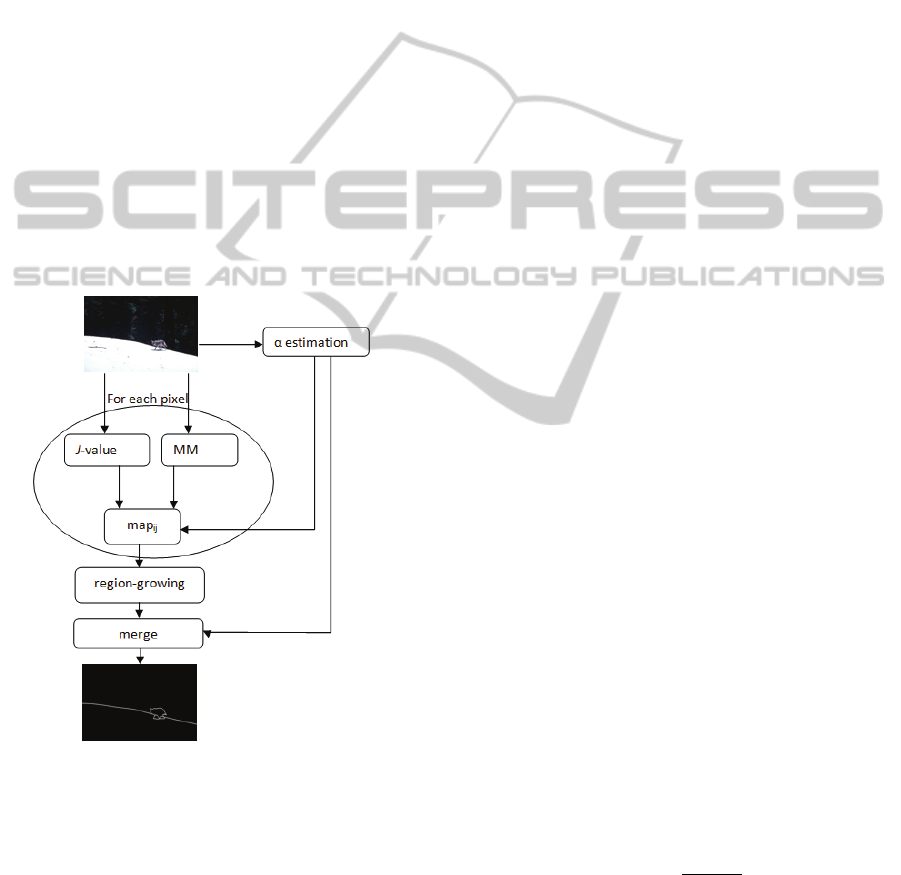
system. The global estimated value α controls two
process:
1) the local integration of the J-value and local
Fractal-value. Each pixel of the 3D terrain map is
now calculated as:
map
i
j
= J-value×α
norm
+ (1-α
norm
)×Fractal-value, (1)
where α
norm
= α/max(α
i
), i indexing the 200 images
used as training set (provided by BSDS). For low α
values, the image presents more texture, and the
multifractal weight is greater than that of the J-
value, as multifractal models textures in a better way
than the J-value;
2) the threshold used in region merging is
(0.4×α
norm
), where 0.4 is the default value for the
JSEG method. The lower the threshold is, lesser
regions will be merged, and the segmentation result
will present more regions with a lower threshold,
compared to a higher threshold. An image with high
α value presents large objects and smooth edges, so
it is expected that the segmentation result will
present just a few regions.
Figure 2: Simplified architecture of MM-Frac.
2.2 Second-Level of Integration
2.2.1 Edge Detection
We considered here some classical edge detectors
(Sobel, Prewitt, Laplacian and morphological
gradient), which generates an output known as a soft
boundary map, with each pixel valued from zero to
one, where higher values mean greater confidence in
the existence of a boundary. To choose a good edge
detector, it was made a preliminary test and the
morphological gradient presents the overall F-
measure slightly better than the other detectors.
Therefore, it was chosen as the edge detection
method.
It is quite usual to smooth the image to eliminate
noise before the edge detection. We choose a
classical non-linear edge-preserving-smoothing
filter, the Kuwahara filter with 5×5 mask size. To
process a color image, each of three color channels,
RGB, is processed separately, and then all results are
added into one image.
2.2.2 Second-level of Integration: KSS
The integration method is independent of how the
edge-map and region-map are processed. However,
it is necessary that the region-map be a binary image
and the edge-map be a soft map. Figure 3 shows a
simplified architecture of the proposed KSS system.
First, we will present the algorithm as a pseudocode:
1. Inputs: edge-map and region-map
2. Set image-result as the sum of edge-map and region-
map
3. Build a weak-edge-map from edge-map
4. For each pixel
I. If (the pixel is marked as edge on region-map
and the pixel is marked as a weak on weak-edge-
map and the majority of neighborhood is marked as
a weak on weak-edge-map).
Then set non-edge in the pixel location in the
resulting image.
II. If (the pixel is marked as a non-edge on
region-map and the pixel is marked as a weak on
weak-edge-map).
Then set non-edge in the pixel location in the
resulting image.
In the step-2, the sum operation will enhance all
boundary pixels that match in the two different input
maps. In the rest of the code, the logic is to eliminate
or reduce false information. In the step-3,the purpose
is to detect the weak edges from the edge-map. To
automate the threshold value, it was used an idea
similar to the one in Rotem, Greenspan and
Goldberger (2007), the value of the threshold is
based on edge-map histogram h, and is given by
ℎℎ
=
∑
ℎ
∑
ℎ
,
(2)
where i=[0,255] is the value of a pixel in the image.
A noisy edge-map will result in low values of
threshold
weak
while a strongly defined edge-map will
result in higher values. Step-4.I eliminates false
boundaries provided by region-map and step-4.II
TWO-LEVEL STRATEGY FOR IMAGE BOUNDARY DETECTION
183

eliminates the noisy information provided by the
edge-map source. The neighbourhood of KSS weak-
edge-map was set to 3×3 for all images.
The higher the threshold
weak
value is, more weak-
edges are obtained, and thus more information will
be eliminated in the process. The result presents less
edge information in the region-map and less weak
information in the edge-map. The result seems
cleaner, preserving only the strong edges of both
maps. However, when the image is noisy, all
information about both maps is preserved, with the
strong edges emphasized. In such images, we notice
that region-map information is more valuable than
edge-map information.
Figure 3: Simplified architecture of KSS.
3 EXPERIMENTAL RESULTS
AND DISCUSSION
We tested our proposed method with natural colored
images provided by the BSDS image dataset,
applying it to all one hundred images of the test
dataset. The BSDS binarize the boundary map at
many levels, according to the threshold parameter
(the chosen value is 10).
Figure 4 shows some results, where (a) shows
the input image, (b) the human benchmark and the
segmentation result of (c) corresponds to JSEG, (d)
MM-Frac, (e) morphological gradient edge detection
and (f) result of KSS process, already binarized in
the best threshold computed by the BSDS. Each
result has its computed F-measure metric.
In a qualitatively comparison, the original JSEG
algorithm tends to over-segment images, splitting
objects into several smaller regions. The MM-Frac
approach, by its turn, significantly decreases over-
segmentation. For an example, the trees in the
background in the first image are not segmented as
in the JSEG result. Moreover, the results present
more accurate boundaries when compared to the
human benchmark. In the second line, the boundary
encompasses the entire body of the snake and not
fragments.
In the fifth column, the results of edge detection
are presented. The results are very noisy and this is
mainly due to the fact that edge detection techniques
rely entirely on the local information available in the
image. The edge-map responds to all contrast
variations over the texture regions, like in the sand
area on the second line of Figure 4. At the same
time, the method of edge detection is responsible for
highlighting details such as the stick in the left in the
snow area in the first line of Figure 4 and the insect
near to the snake in the second image of Figure 4.
The results for the KSS method are presented in
the last column. Details detected using edge
detection method are kept, but the noise was
attenuated and disappears after the binarization
computed by BSDS. Now, the boundaries are more
accurate and are closer to the human perception.
Deng and Manjunath (2001) pointed out that the
major problem they observed in JSEG result is
caused by the varying shades due to the illumination.
For instance, the color of a sky can vary in a very
smooth transition as in the image BSDS image
42049, the last line of Figure 4. Visually, there is no
clear boundary. However, the JSEG result presents a
circle region in the image. The human perception
does not perceive this smooth varying of color as a
different region. The result after KSS does not
present this false boundary. The smooth is not
perceived by the edge detection, and then the
boundary is erased by the KSS method.
Quantitatively speaking, the metrics recall,
precision and F-measure of each method computed
by the BSDS are tabbed in the superior part of Table
1.
MM-Frac approach improves the recall metric
without decreasing precision, thus raising the F-
measure score a little bit. Edge detection looses in
terms of precision, because of the noisy pixels.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
184

Input Image
Human
Benchmark
JSEG MM-Frac Edge Detection KSS
167062 F-measure = 0.95
F-measure = 0.62
F-measure=0.88
F-measure=0.92
F-measure=0.94
196073
F-measure = 0.85
F-measure=0.55
F-measure=0.74 F-measure=0.70
F-measure=0.79
41033
F-measure = 0.88
F-measure=0.56 F-measure=0.62
F-measure=0.60
F-measure = 0.66
42049
(a)
F-measure = 0.96
(b)
F-measure = 0.75
(c)
F-measure = 0.58
(d)
F-measure = 0.93
(e)
F-measure = 0.91
(f)
Figura 4: (a) Input image (b) Human benchmark (c) JSEG result (d) MM-Frac result (e) Edge Detection result (f) KSS
result in the best threshold.
After KSS method, the F-measure increases to 0.61,
this is the closest value, comparing to the human
perception.
Table 1: Metrics of each method computed by BSDS.
Human
JSEG
MM-Frac
Edge
Detection
After
KSS
B
S
D
S
Recall 0.70 0.61 0.63 0.65 0.69
Precision 0.89 0.56 0.56 0.49 0.54
F-measure 0.79 0.58 0.59 0.56 0.61
m
e
a
n
Recall 0.70 0.61 0.63 0.69 0.73
Precision 0.89 0.57 0.57 0.55 0.57
F-measure 0.78 0.58 0.59 0.59 0.63
BSDS computes the maximum F-measure value
across the precision-recall curve, for which each
point corresponds to an image in the test dataset.
Differently, bottom part of Table 1 shows the
average value of the same three metrics, for the one
hundred images available in the test dataset. From
such average values, the advantage of the proposed
two-level strategy becomes much clearer.
4 CONCLUSIONS
This work proposes a new two-level approach to
boundary detection for natural color images. In the
first level we embedded a MM in the classical JSEG
algorithm. The integration, called MM-Frac, is
controlled by the slope of the image power
spectrum. One conclusion is that the MM improves
the sensitivity to boundary regions, thus providing
segmentation results that match the human
perception better than the segmentation results
associated with the original JSEG algorithm.
In the second-level, the post-processing
integration, the main goal is to integrate the region-
growing result from MM-Frac and edge information.
Our strategy, called KSS, is to put together the two
maps, eliminating the false boundaries in region-
TWO-LEVEL STRATEGY FOR IMAGE BOUNDARY DETECTION
185

map, based on edge information, and eliminating the
noisy edges in the edge-map, based on region
information. The KSS algorithm works well and
solves the problem of false boundaries pointed out in
other works. Furthermore, all strong edges of both
input maps are held, improving the boundary
detection. Unfortunately, the KSS results present
broken edges, not keeping the contour closed.
The conclusion is that the two-level approach
proposed here improves the boundary detection
results, generating segmented images that match the
human perception better than the results associated
to the individual methods used in the architecture.
ACKNOWLEDGEMENTS
The authors would like to thank CAPES (Brazil) for
financial support.
REFERENCES
Chaudhuri, B. B.; Sarkar, N., 1995. Texture segmentation
using fractal dimension, IEEE Trans. Pattern Anal.
Mach. Intell., 17 (1), 72–77.
Côco, K. F., Salles, E. O. T., Sarcinelli-Filho, M., 2009.
Topographic independent component analysis based
on fractal and morphology applied to texture
segmentation, Lecture Notes in Computer Science,
5441, 491-498.
Deng, Y., Manjunath, B. S., 2001. Unsupervised
segmentation of color-texture regions in images and
video, IEEE Trans. Pattern Anal. Mach. Intell., 23 (8).
Komati, K. S., Salles, E. O. T., Sarcinelli-Filho, M., 2010.
Unsupervised color image segmentation based on local
fractal dimension, In Proc. 17th International
Conference on Systems, Signals and Image Processing
(IWSSIP 2010), 1, 243-246.
Komati, K. S., Salles, E. O. T., Sarcinelli-Filho, M., in
press. A Strategy for Image Boundary Detection
Combining Region and Edge Maps, Computing in
Science and Engineering, IEEE computer Society
Digital Library. doi: 10.1109/MCSE.2010.148.
Martin, D., Fowlkes, C., Tal, D., Malik, J., 2001. A
database of human segmented natural images and its
application to evaluating segmentation algorithms and
measuring ecological statistics, In Proc. 8th IEEE Int´l
Conf. Computer Vision, 2, 416–423.
Martin, D. R., Fowlkes, C. C., Malik, J., 2004. Learning to
detect natural image boundaries using local brightness,
color, and texture cues, IEEE Trans. Pattern Anal.
Mach. Intell., 26(5), 530–549, 2004.
Muñoz, X., Freixenet, J., Cufí, X., Martí, J., 2003.
Strategies for image segmentation combining region
and boundary information, IEEE Pattern Recognition
Letters, 24(1-3), 375–392.
Pentland, A. P., 1984 Fractal-based description of natural
scenes. IEEE Trans. on Pattern Analysis and Machine
Intelligence, 6.
Rotem, O., Greenspan, H., Goldberger, J., 2007.
Combining Region and Edge Cues for Image
Segmentation in a Probabilistic Gaussian Mixture
Framework. In Proc 2007 IEEE Conference on
Computer Vision and Pattern Recognition, 1-8.
Torralba, A., Oliva, A., 2003. Statistics of natural image
categories, Institute of Physics Publishing:
Computation in Neural Systems, 14, 391-412.
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
186
