ACTION RECOGNITION BASED ON MULTI-LEVEL

REPRESENTATION OF 3D SHAPE

Binu M. Nair and Vijayan K. Asari

Department of Electrical and Computer Engineering, University of Dayton, Dayton, Ohio, U.S.A.

Keywords:

Spacetime shape, Radon transform, Distance transform, Shape descriptor.

Abstract:

A novel algorithm has been proposed for recognizing human actions using a combination of shape descrip-

tors. Every human action is considered as a 3D space time shape and the shape descriptors based on the 3D

Euclidean distance transform and the Radon transform are used for its representation. The Euclidean distance

transform gives a suitable internal representation where the interior values correspond to the action performed.

By taking the gradient of this distance transform, the space time shape is divided into different number of

levels with each level representating a coarser version of the original space time shape. Then, at each level and

at each frame, the Radon transform is applied from where action features are extracted. The action features

are the R-Transform feature set which gives the posture variations of the human body with respect to time and

the R-Translation vector set which gives the translatory variation. The combination of these action features is

used in a nearest neighbour classiﬁer for action recognition.

1 INTRODUCTION

Human action recognition has been a widely re-

searched area in computer vision as it holds a lot of

applications relating to security and surveillance. One

such application is the human action detection and

recognition algorithm implemented in systems using

CCTV cameras where the system is used for detecting

suspicious human behavior and alerting the authori-

ties accordingly (C. J .Cohen et al., 2008). Another

area is in object recognition where, by evaluating the

human interaction with the object and recognizing the

human action, the particular object is recognized (M.

Mitani et al., 2006). Thus arises the need for faster

and robust algorithms for human action recognition.

Action recognition involves the extraction of

suitable distinguishable features representing certain

variations in the human body caused due to the action.

One approach involves the use of 2D or 3D shape de-

scriptors to represent a space time shape which is a

concatenation of human silhouettes across time. An-

other approach involves the computation of certain lo-

calised motion ﬁelds and trajectories of speciﬁc points

from a space time shape. The various invariant prop-

erties extracted from these motion ﬁelds and trajecto-

ries are then considered as action features. In the algo-

rithm proposed in this paper, a combination of shape

descriptors are used for the representation of the space

time shape and the extraction of action features. This

algorithm is closely related to the action recognition

framework based on Poisson’s shape descriptor (M.

Blank et al., 2005) and the shape descriptor based on

the Radon transform (Y. Wang et al., 2007).

In the next section, a review of the algorithms that

have been proposed over the last few years for action

recognition, is explained brieﬂy. The algorithms de-

scribed are mainly based on the motion ﬁelds and the

shape descriptors. In the third section, the proposed

algorithm for action recognition is explained in detail

with illustrations. Results are provided in the fourth

section where the recognition rates are compared with

those of other algorithms. The variation of the accu-

racies with respect to certain parameters of the algo-

rithm are also given. Finally, the paper concludes the

algorithm by mentioning the pros and cons and dis-

cusses the improvements and the future work.

2 PREVIOUS WORK

In this section, we shall go through some of the works

which are based on motion ﬁelds, shape descriptors

and trajectories of tracked body parts.

378

M. Nair B. and K. Asari V..

ACTION RECOGNITION BASED ON MULTI-LEVEL REPRESENTATION OF 3D SHAPE.

DOI: 10.5220/0003376303780386

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 378-386

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Segmentation of Dog silhouette given in (S.Tabbone et al., 2006).

2 PREVIOUS WORK

In this section, we shall go through some of the works

which are based on motion ﬁelds, shape descriptors

and trajectories of tracked body parts.

2.1 Algorithms Based on Motion

Capture Fields or Trajectories

Earlier works in action recognition makes use of

temporal templates such as motion history images

(J.W.Davis and A.F.Bobick, 1997), the timed mo-

tion history images (G.R.Bradski and J.W.Davis,

2000) and the hierarchical motion history images

(J.W.Davis, 2003) where these templates provides the

motion characteristics such as the motion history im-

age and motion energy image at every spatial location

of a frame in an image sequence. Some of the features

extracted are the optical ﬂow vectors from the MHI

gradient, the radial histogram and local and global

orientation computed at each pixel (G.R.Bradski and

J.W.Davis, 2000). The speed of motion of a body

movement was incorporated by computing the MHI

from scaled versions of the images and extracting the

motion ﬁelds from each level (J.W.Davis, 2003).

Motion descriptors based purely on the optical

ﬂow measurements computed from each pixel of

the video frame are used to describe an action of

an individual at a far off distance from the camera

(A.A.Efros et al., 2003). These optical ﬂow mea-

surements are calculated from a ﬁgure-centric spatio-

temporal volume using the Lucas-Kanade algorithm.

The time variation of the optical ﬂow vector computed

is considered as an action feature which are compared

by a correlation based similarity measure.

Algorithms proposed in (J.C.Niebles et al., 2006;

P.Scovanner et al., 2007) consider action features as

codewords in a codebook where these features are ex-

tracted from interest regions in a space time shape.

In (J.C.Niebles et al., 2006), the interest regions are

the local maxima regions of a response function de-

ﬁned by a combination of a Gaussian and a Gabor

ﬁlter computed at every frame and the extracted fea-

tures are the gradient and the optical ﬂow from these

regions while in (P.Scovanner et al., 2007), the inter-

est regions are obtained by random sampling of the

pixels at different locations, time and scale and the

3D SIFT descriptors extracted from these regions are

taken as the action features.

Some of the works proposed a particular model

which includes tracking or segmenting of various

parts of the human body. In (S.Ali et al., 2007), hu-

man actions have been modelled as a non-linear dy-

namical system where the state variables are deﬁned

by the reference joints in the human body silhouette

and their functions are deﬁned by their trajectories.

Here, action features are derived by analysing the tra-

jectories as a time series data and extracting the in-

variant properties. Many methods are available for

studying the time series data but the one used here

applies the theory of chaotic systems to analyze the

non-linear nature (J.Zhang et al., 1998).

The concept of mid-level features known as space

time shapelets is introduced in (D.Batra et al., 2008)

where these shapelets are local volumetric objects or

local 3D shapes extracted from a space time shape.

Thus, an action is represented by a combination of

such shapelets as these represent the motion charac-

teristics on a more localised level. Extracting all the

possible such volumes from each space time shape

of the database and clustering these sub-volumes pro-

vides the cluster centers which are then considered as

space time shapelets.

2.2 Algorithms Based on Shape

Descriptors

Shape descriptors (D.Zhang and G.Lu, 2003; Q.Chen

et al., 2004; A.Khotanzad and Y.H.Hong, 1990;

M.K.Hu, 2008) can be used to extract the variation of

the silhouettes across the video frames. Better vari-

ations can be extracted using shape descriptors such

as the one based on Poisson’s equation (L.Gorelick

et al., 2004) and the one based on the Radon transform

(S.Tabbone et al., 2006). This is because they not only

give the boundary representation of a silhouette of a

3D shape but also give an internal representation. A

brief discussion on these algorithms will be provided

as these form the basis for the algorithm proposed in

this paper.

In (M.Blank et al., 2005), the concept of a space

time shape is introduced where a space time shape

Figure 1: Segmentation of Dog silhouette given in (S. Tabbone et al., 2006).

2.1 Algorithms based on Motion

Capture Fields or Trajectories

Earlier works in action recognition makes use of tem-

poral templates such as motion history images (J.

W. Davis and A. F. Bobick, 1997), the timed mo-

tion history images (G. R. Bradski and J.W.Davis,

2000) and the hierarchical motion history images (J.

W. Davis, 2003) where these templates provides the

motion characteristics such as the motion history im-

age and motion energy image at every spatial loca-

tion of a frame in an image sequence. Some of the

features extracted are the optical ﬂow vectors from

the MHI gradient, the radial histogram and local and

global orientation computed at each pixel (G. R. Brad-

ski and J.W.Davis, 2000). The speed of motion of a

body movement was incorporated by computing the

MHI from scaled versions of the images and extract-

ing the motion ﬁelds from each level (J. W. Davis,

2003).

Motion descriptors based purely on the optical

ﬂow measurements computed from each pixel of the

video frame are used to describe an action of an in-

dividual at a far off distance from the camera (A. A.

Efros et al., 2003). These optical ﬂow measurements

are calculated from a ﬁgure-centric spatio-temporal

volume using the Lucas-Kanade algorithm. The time

variation of the optical ﬂow vector computed is con-

sidered as an action feature which are compared by a

correlation based similarity measure.

Algorithms proposed in (J. C. Niebles et al., 2006;

P. Scovanner et al., 2007) consider action features as

codewords in a codebook where these features are ex-

tracted from interest regions in a space time shape.

In (J. C. Niebles et al., 2006), the interest regions are

the local maxima regions of a response function de-

ﬁned by a combination of a Gaussian and a Gabor

ﬁlter computed at every frame and the extracted fea-

tures are the gradient and the optical ﬂow from these

regions while in (P. Scovanner et al., 2007), the inter-

est regions are obtained by random sampling of the

pixels at different locations, time and scale and the

3D SIFT descriptors extracted from these regions are

taken as the action features.

Some of the works proposed a particular model

which includes tracking or segmenting of various

parts of the human body. In (S. Ali et al., 2007), hu-

man actions have been modelled as a non-linear dy-

namical system where the state variables are deﬁned

by the reference joints in the human body silhouette

and their functions are deﬁned by their trajectories.

Here, action features are derived by analysing the tra-

jectories as a time series data and extracting the in-

variant properties. Many methods are available for

studying the time series data but the one used here

applies the theory of chaotic systems to analyze the

non-linear nature (J. Zhang et al., 1998).

The concept of mid-level features known as space

time shapelets is introduced in (D. Batra et al., 2008)

where these shapelets are local volumetric objects or

local 3D shapes extracted from a space time shape.

Thus, an action is represented by a combination of

such shapelets as these represent the motion charac-

teristics on a more localised level. Extracting all the

possible such volumes from each space time shape

of the database and clustering these sub-volumes pro-

vides the cluster centers which are then considered as

space time shapelets.

2.2 Algorithms based on Shape

Descriptors

Shape descriptors (D. Zhang and G. Lu, 2003; Q.

Chen et al., 2004; A. Khotanzad and Y. H. Hong,

1990; M. K. Hu, 2008) can be used to extract the vari-

ation of the silhouettes across the video frames. Bet-

ter variations can be extracted using shape descrip-

tors such as the one based on Poisson’s equation (L.

Gorelick et al., 2004) and the one based on the Radon

transform (S. Tabbone et al., 2006). This is because

they not only give the boundary representation of a

silhouette of a 3D shape but also give an internal rep-

resentation. A brief discussion on these algorithms

will be provided as these form the basis for the algo-

rithm proposed in this paper.

In (M. Blank et al., 2005), the concept of a space

time shape is introduced where a space time shape

is formed by the concatenation of silhouettes in the

video frames and considering actions as 3D shapes.

The shape descriptors based on the Poisson’s equa-

tion in 3D used to represent the space time shape and

various properties such as local space-time saliency,

shape structure, action dynamics and local orientation

ACTION RECOGNITION BASED ON MULTI-LEVEL REPRESENTATION OF 3D SHAPE

379

are extracted. A shape descriptor based on the Radon

transform (R. N. Bracewell, 1995) known as the R-

Transform is deﬁned in (Y. Wang et al., 2007). This

transform is used to represent the low-level features

in a binary silhouette in a single frame and these are

used in the training of hidden Markov models to rec-

ognize the action.

A combination of shape ﬂow and motion ﬂow

features have been used as action features in

(A.Mohiuddin and S.W.Lee, 2008) where the shape

ﬂow features are a combination of different moment

based shape descriptors and the motion ﬂow feature

is the optical ﬂow. The shape descriptors used are

the Hu’s invariant moments (M. K. Hu, 2008) and

Zernike moments (A. Khotanzad and Y. H. Hong,

1990). In (X. Sun et al., 2009), instead of using op-

tical ﬂow feature vectors to represent the local fea-

tures, both 2D and 3D SIFT descriptors are used while

the global features extracted are the Zernike moments

from the motion energy images. The 2D SIFT de-

scriptor emphasizes the 2D silhouette shape and the

3D SIFT descriptor emphasizes the motion.

3 MULTI-LEVEL SHAPE

REPRESENTATION

We shall ﬁrst review the multi-level representation of

a 2D shape using the R-Transform which is proposed

in (S. Tabbone et al., 2006). First, the distance trans-

form (G. Borgefors, 1984; D. W. Paglieroni, 1992; A.

Rosenfeld and J. Pfaltz, 1966) based on the Euclidean

distance is computed for that shape. The computation

involves the approximation of the Euclidean distance

transform and this approximation is the (3,4) Chamfer

distance transform. Using the values obtained from

the transform, the 2D shape is segmented into dif-

ferent levels using a predeﬁned threshold. The levels

correspond to the coarseness of the shape and this is

illustrated in Figure 1. As shown, the silhoutte of a

dog has been segmented into 8 different levels. Now,

at each of these levels, the R-transform is computed

which can be deﬁned as

(α) =

+∞

−∞

(s,α)ds (1)

where T (s,α) is the radon transform of the 2D bi-

nary image. As proved in (S. Tabbone et al., 2006),

the R-Transform is translation invariant and is made

scale invariant by normalizing it with its area. Since

it is not rotation invariant, the scaled magnitude of

the discrete Fourier transform is computed. There-

fore, the multi-level representation of 2D shape is the

set of magnitudes of the discrete Fourier transform of

the R-Transform at each level of the shape.

4 PROPOSED ALGORITHM

The proposed algorithm is an application of the multi-

level shape representation to a space time shape which

provides the necessary features of action classiﬁca-

tion. The 3D Euclidean distance transform (P. F.

Felzenszwalb and D. P. Huttenlocher, 2004) gives the

internal representation where its gradient is used to di-

vide the space time shape into different levels. Then,

at each level, the R-Transform and the R-Translation

features are extracted and these are considered as suit-

able action features. The various steps involved in the

algorithm are explained in detail in this section.

is formed by the concatenation of silhouettes in the

video frames and considering actions as 3D shapes.

The shape descriptors based on the Poisson’s equa-

tion in 3D used to represent the space time shape and

various properties such as local space-time saliency,

shape structure, action dynamics and local orienta-

tion are extracted. A shape descriptor based on the

Radon transform (R.N.Bracewell, 1995) known as the

R-Transform is deﬁned in (Y.Wang et al., 2007). This

transform is used to represent the low-level features

in a binary silhouette in a single frame and these are

used in the training of hidden Markov models to rec-

ognize the action.

A combination of shape ﬂow and motion ﬂow

features have been used as action features in

(A.Mohiuddin and S.W.Lee, 2008) where the shape

ﬂow features are a combination of different moment

based shape descriptors and the motion ﬂow feature

is the optical ﬂow. The shape descriptors used are the

Hu’s invariant moments (M.K.Hu, 2008) and Zernike

moments (A.Khotanzad and Y.H.Hong, 1990). In

(X.Sun et al., 2009), instead of using optical ﬂow fea-

ture vectors to represent the local features, both 2D

and 3D SIFT descriptors are used while the global

features extracted are the Zernike moments from the

motion energy images. The 2D SIFT descriptor em-

phasizes the 2D silhouette shape and the 3D SIFT de-

scriptor emphasizes the motion.

3 MULTI-LEVEL SHAPE

REPRESENTATION

We shall ﬁrst review the multi-level representation

of a 2D shape using the R-Transform which is pro-

posed in (S.Tabbone et al., 2006). First, the dis-

tance transform (G.Borgefors, 1984; D.W.Paglieroni,

1992; A.Rosenfeld and J.Pfaltz, 1966) based on the

Euclidean distance is computed for that shape. The

computation involves the approximation of the Eu-

clidean distance transform and this approximation is

the (3,4) Chamfer distance transform. Using the val-

ues obtained from the transform, the 2D shape is seg-

mented into different levels using a predeﬁned thresh-

old. The levels correspond to the coarseness of the

shape and this is illustrated in Figure 1. As shown, the

silhoutte of a dog has been segmented into 8 different

levels. Now, at each of these levels, the R-transform

is computed which can be deﬁned as

(α) =

+∞

−∞

(s,α)ds (1)

where T (s,α) is the radon transform of the 2D bi-

nary image. As proved in (S.Tabbone et al., 2006),

the R-Transform is translation invariant and is made

scale invariant by normalizing it with its area. Since

it is not rotation invariant, the scaled magnitude of

the discrete Fourier transform is computed. There-

fore, the multi-level representation of 2D shape is the

set of magnitudes of the discrete Fourier transform of

the R-Transform at each level of the shape.

4 PROPOSED ALGORITHM

The proposed algorithm is an application of the multi-

level shape representation to a space time shape

which provides the necessary features of action clas-

siﬁcation. The 3D Euclidean distance transform

(P.F.Felzenszwalb and D.P.Huttenlocher, 2004) gives

the internal representation where its gradient is used

to divide the space time shape into different lev-

els. Then, at each level, the R-Transform and the R-

Translation features are extracted and these are con-

sidered as suitable action features. The various steps

involved in the algorithm are explained in detail in

this section.

Figure 2: Extraction of a silhouette from a video frame.

Figure 3: Space time shapes of jumping jack and walk ac-

tions.

4.1 Silhouette Extraction and

Formation of Space-time shapes.

First, the silhouettes are extracted from each frame of

the video sequence by comparing it with its median

background and then, thresholding, dilating and erod-

ing to form the binary silhouette image shown in Fig-

ure 2. Once the silhouettes are extracted, a predeﬁned

number are concatenated to form the 3D space time

Figure 2: Extraction of a silhouette from a video frame.

is formed by the concatenation of silhouettes in the

video frames and considering actions as 3D shapes.

The shape descriptors based on the Poisson’s equa-

tion in 3D used to represent the space time shape and

various properties such as local space-time saliency,

shape structure, action dynamics and local orienta-

tion are extracted. A shape descriptor based on the

Radon transform (R.N.Bracewell, 1995) known as the

R-Transform is deﬁned in (Y.Wang et al., 2007). This

transform is used to represent the low-level features

in a binary silhouette in a single frame and these are

used in the training of hidden Markov models to rec-

ognize the action.

A combination of shape ﬂow and motion ﬂow

features have been used as action features in

(A.Mohiuddin and S.W.Lee, 2008) where the shape

ﬂow features are a combination of different moment

based shape descriptors and the motion ﬂow feature

is the optical ﬂow. The shape descriptors used are the

Hu’s invariant moments (M.K.Hu, 2008) and Zernike

moments (A.Khotanzad and Y.H.Hong, 1990). In

(X.Sun et al., 2009), instead of using optical ﬂow fea-

ture vectors to represent the local features, both 2D

and 3D SIFT descriptors are used while the global

features extracted are the Zernike moments from the

motion energy images. The 2D SIFT descriptor em-

phasizes the 2D silhouette shape and the 3D SIFT de-

scriptor emphasizes the motion.

3 MULTI-LEVEL SHAPE

REPRESENTATION

We shall ﬁrst review the multi-level representation

of a 2D shape using the R-Transform which is pro-

posed in (S.Tabbone et al., 2006). First, the dis-

tance transform (G.Borgefors, 1984; D.W.Paglieroni,

1992; A.Rosenfeld and J.Pfaltz, 1966) based on the

Euclidean distance is computed for that shape. The

computation involves the approximation of the Eu-

clidean distance transform and this approximation is

the (3,4) Chamfer distance transform. Using the val-

ues obtained from the transform, the 2D shape is seg-

mented into different levels using a predeﬁned thresh-

old. The levels correspond to the coarseness of the

shape and this is illustrated in Figure 1. As shown, the

silhoutte of a dog has been segmented into 8 different

levels. Now, at each of these levels, the R-transform

is computed which can be deﬁned as

(α) =

+∞

−∞

(s,α)ds (1)

where T (s,α) is the radon transform of the 2D bi-

nary image. As proved in (S.Tabbone et al., 2006),

the R-Transform is translation invariant and is made

scale invariant by normalizing it with its area. Since

it is not rotation invariant, the scaled magnitude of

the discrete Fourier transform is computed. There-

fore, the multi-level representation of 2D shape is the

set of magnitudes of the discrete Fourier transform of

the R-Transform at each level of the shape.

4 PROPOSED ALGORITHM

The proposed algorithm is an application of the multi-

level shape representation to a space time shape

which provides the necessary features of action clas-

siﬁcation. The 3D Euclidean distance transform

(P.F.Felzenszwalb and D.P.Huttenlocher, 2004) gives

the internal representation where its gradient is used

to divide the space time shape into different lev-

els. Then, at each level, the R-Transform and the R-

Translation features are extracted and these are con-

sidered as suitable action features. The various steps

involved in the algorithm are explained in detail in

this section.

Figure 2: Extraction of a silhouette from a video frame.

Figure 3: Space time shapes of jumping jack and walk ac-

tions.

4.1 Silhouette Extraction and

Formation of Space-time shapes.

First, the silhouettes are extracted from each frame of

the video sequence by comparing it with its median

background and then, thresholding, dilating and erod-

ing to form the binary silhouette image shown in Fig-

ure 2. Once the silhouettes are extracted, a predeﬁned

number are concatenated to form the 3D space time

Figure 3: Space time shapes of jumping jack and walk ac-

tions.

4.1 Silhouette Extraction and

Formation of Space-time Shapes

First, the silhouettes are extracted from each frame of

the video sequence by comparing it with its median

background and then, thresholding, dilating and erod-

ing to form the binary silhouette image shown in Fig-

ure 2. Once the silhouettes are extracted, a predeﬁned

number are concatenated to form the 3D space time

shapes with axes x,y and t. The space time shapes are

shown in Figure 3.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

380

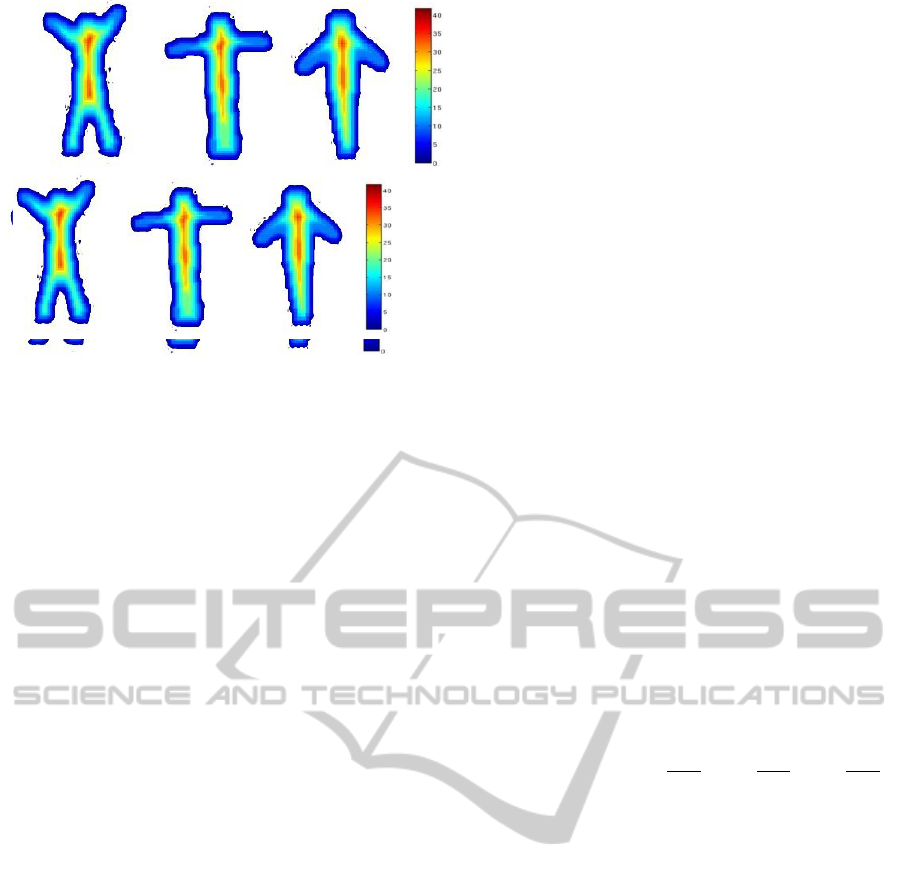
Figure 4: Sample Frames of the distance transformed space

time shape formed from 10 silhouttes.

Figure 5: Sample frames of the gradient of the distance

transformed shape.

shapes with axes x, y and t. The space time shapes are

shown in Figure 3.

4.2 Computation of Euclidean Distance

Transform

To segment the space time shape, the 3D distance

transform (P.F.Felzenszwalb and D.P.Huttenlocher,

2004) based on the Euclidean distance is computed.

This transformation assigns to a interior voxel a value

which is proportional to the Euclidean distance be-

tween this voxel and the nearest boundary voxel. The

computation involves the use of a 3-pass algorithm

where each pass is associated with a raster scan of the

entire space time shape in a particular dimension us-

ing a 1D mask.

The minimum distance calculation is done by

ﬁnding the local minima of the lower envelope of the

set of parabolas where each parabola is deﬁned on the

basis of the Euclidean distance between two points

(P.F.Felzenszwalb and D.P.Huttenlocher, 2004). The

intermediate distance transform vales computed in the

ﬁrst pass is based directly on the Euclidean distance.

In the next two passes, the distance transform values

are computed from the set of parabolas deﬁned on the

boundary voxels in the respective dimension. This

type of distance transform is given by

(p) = min

qε B

((p − q)

+ f (q)) (2)

where p is a non-boundary point, q is a boundary

point, B is the boundary and f (q) is the value of the

distance measure between points p and q. It is seen

that for every qεB, the distance transform is bounded

by the parabola rooted at (q, f (q)). In short, the dis-

tance transform value at point p is the minima of the

lower envelope of the parabolas formed from every

boundary point q. The distance transformation of the

space time shape is shown in Figure 4. It is seen

that the area covered by the torso part of the body

has higher values than the area covered by the limbs.

By varying the aspect ratio, the different axes x,y and

t will have different emphasis on the computed dis-

tance transform.

4.3 Segmentation of the 3D Space-time

Shape

Human actions are distinguished from the variation

of the silhouette and these variations are more along

the limbs than in the torso. So, a better representation

of the space time shape is required which emphasizes

fast moving parts so that the features extracted gives

the necessary variation to represent the action. Thus, a

normalized gradient of the distance transform is used

and, as shown in Figure 5, the fast moving parts such

as the limbs have higher values compared to the torso

region. The gradient of the space time shape φ(x,y,t)

(M.Blank et al., 2005) is deﬁned as

φ(x,y,t) = U (x,y,t) +K

∂

∂x

∂

∂y

∂

∂t

(3)

Figure 6: 8-Level segmentation of sample frames of the

space time shape of the “Jumping-Jack” action.

where U(x,y,t) is the distance transformed space time

shape, K

is the weight added to the derivative taken

along the i

axis. The weights associated with the

Figure 4: Sample Frames of the distance transformed space

time shape formed from 10 silhouttes.

Figure 4: Sample Frames of the distance transformed space

time shape formed from 10 silhouttes.

Figure 5: Sample frames of the gradient of the distance

transformed shape.

shapes with axes x,y and t. The space time shapes are

shown in Figure 3.

4.2 Computation of Euclidean Distance

Transform

To segment the space time shape, the 3D distance

transform (P.F.Felzenszwalb and D.P.Huttenlocher,

2004) based on the Euclidean distance is computed.

This transformation assigns to a interior voxel a value

which is proportional to the Euclidean distance be-

tween this voxel and the nearest boundary voxel. The

computation involves the use of a 3-pass algorithm

where each pass is associated with a raster scan of the

entire space time shape in a particular dimension us-

ing a 1D mask.

The minimum distance calculation is done by

ﬁnding the local minima of the lower envelope of the

set of parabolas where each parabola is deﬁned on the

basis of the Euclidean distance between two points

(P.F.Felzenszwalb and D.P.Huttenlocher, 2004). The

intermediate distance transform vales computed in the

ﬁrst pass is based directly on the Euclidean distance.

In the next two passes, the distance transform values

are computed from the set of parabolas deﬁned on the

boundary voxels in the respective dimension. This

type of distance transform is given by

(p) = min

qε B

((p − q)

+ f (q)) (2)

where p is a non-boundary point, q is a boundary

point, B is the boundary and f (q) is the value of the

distance measure between points p and q. It is seen

that for every qεB, the distance transform is bounded

by the parabola rooted at (q, f (q)). In short, the dis-

tance transform value at point p is the minima of the

lower envelope of the parabolas formed from every

boundary point q. The distance transformation of the

space time shape is shown in Figure 4. It is seen

that the area covered by the torso part of the body

has higher values than the area covered by the limbs.

By varying the aspect ratio, the different axes x,y and

t will have different emphasis on the computed dis-

tance transform.

4.3 Segmentation of the 3D Space-time

Shape

Human actions are distinguished from the variation

of the silhouette and these variations are more along

the limbs than in the torso. So, a better representation

of the space time shape is required which emphasizes

fast moving parts so that the features extracted gives

the necessary variation to represent the action. Thus, a

normalized gradient of the distance transform is used

and, as shown in Figure 5, the fast moving parts such

as the limbs have higher values compared to the torso

region. The gradient of the space time shape φ(x,y,t)

(M.Blank et al., 2005) is deﬁned as

φ(x,y,t) = U(x, y,t)+K

∂

∂x

∂

∂y

∂

∂t

(3)

Figure 6: 8-Level segmentation of sample frames of the

space time shape of the “Jumping-Jack” action.

where U(x,y,t) is the distance transformed space time

shape, K

is the weight added to the derivative taken

along the i

axis. The weights associated with the

Figure 5: Sample frames of the gradient of the distance

transformed shape.

4.2 Computation of Euclidean Distance

Transform

To segment the space time shape, the 3D distance

transform (P. F. Felzenszwalb and D. P. Huttenlocher,

2004) based on the Euclidean distance is computed.

This transformation assigns to a interior voxel a value

which is proportional to the Euclidean distance be-

tween this voxel and the nearest boundary voxel. The

computation involves the use of a 3-pass algorithm

where each pass is associated with a raster scan of the

entire space time shape in a particular dimension us-

ing a 1D mask.

The minimum distance calculation is done by

ﬁnding the local minima of the lower envelope of the

set of parabolas where each parabola is deﬁned on the

basis of the Euclidean distance between two points (P.

F. Felzenszwalb and D. P. Huttenlocher, 2004). The

intermediate distance transform vales computed in the

ﬁrst pass is based directly on the Euclidean distance.

In the next two passes, the distance transform values

are computed from the set of parabolas deﬁned on the

boundary voxels in the respective dimension. This

type of distance transform is given by

(p) = min

qεB

((p − q)

+ f (q)) (2)

where p is a non-boundary point, q is a boundary

point, B is the boundary and f (q) is the value of the

distance measure between points p and q. It is seen

that for every q εB, the distance transform is bounded

by the parabola rooted at (q, f (q)). In short, the dis-

tance transform value at point p is the minima of the

lower envelope of the parabolas formed from every

boundary point q. The distance transformation of the

space time shape is shown in Figure 4. It is seen

that the area covered by the torso part of the body

has higher values than the area covered by the limbs.

By varying the aspect ratio, the different axes x,y and

t will have different emphasis on the computed dis-

tance transform.

4.3 Segmentation of the 3D Space-time

Shape

Human actions are distinguished from the variation

of the silhouette and these variations are more along

the limbs than in the torso. So, a better representation

of the space time shape is required which emphasizes

fast moving parts so that the features extracted gives

the necessary variation to represent the action. Thus, a

normalized gradient of the distance transform is used

and, as shown in Figure 5, the fast moving parts such

as the limbs have higher values compared to the torso

region. The gradient of the space time shape φ(x,y,t)

(M. Blank et al., 2005) is deﬁned as

φ(x,y,t) = U(x,y,t) + K

∂

∂x

∂

∂y

∂

∂t

(3)

Figure 4: Sample Frames of the distance transformed space

time shape formed from 10 silhouttes.

Figure 5: Sample frames of the gradient of the distance

transformed shape.

shapes with axes x,y and t. The space time shapes are

shown in Figure 3.

4.2 Computation of Euclidean Distance

Transform

To segment the space time shape, the 3D distance

transform (P.F.Felzenszwalb and D.P.Huttenlocher,

2004) based on the Euclidean distance is computed.

This transformation assigns to a interior voxel a value

which is proportional to the Euclidean distance be-

tween this voxel and the nearest boundary voxel. The

computation involves the use of a 3-pass algorithm

where each pass is associated with a raster scan of the

entire space time shape in a particular dimension us-

ing a 1D mask.

The minimum distance calculation is done by

ﬁnding the local minima of the lower envelope of the

set of parabolas where each parabola is deﬁned on the

basis of the Euclidean distance between two points

(P.F.Felzenszwalb and D.P.Huttenlocher, 2004). The

intermediate distance transform vales computed in the

ﬁrst pass is based directly on the Euclidean distance.

In the next two passes, the distance transform values

are computed from the set of parabolas deﬁned on the

boundary voxels in the respective dimension. This

type of distance transform is given by

(p) = min

qε B

((p − q)

+ f (q)) (2)

where p is a non-boundary point, q is a boundary

point, B is the boundary and f (q) is the value of the

distance measure between points p and q. It is seen

that for every qεB, the distance transform is bounded

by the parabola rooted at (q, f (q)). In short, the dis-

tance transform value at point p is the minima of the

lower envelope of the parabolas formed from every

boundary point q. The distance transformation of the

space time shape is shown in Figure 4. It is seen

that the area covered by the torso part of the body

has higher values than the area covered by the limbs.

By varying the aspect ratio, the different axes x,y and

t will have different emphasis on the computed dis-

tance transform.

4.3 Segmentation of the 3D Space-time

Shape

Human actions are distinguished from the variation

of the silhouette and these variations are more along

the limbs than in the torso. So, a better representation

of the space time shape is required which emphasizes

fast moving parts so that the features extracted gives

the necessary variation to represent the action. Thus, a

normalized gradient of the distance transform is used

and, as shown in Figure 5, the fast moving parts such

as the limbs have higher values compared to the torso

region. The gradient of the space time shape φ(x, y,t)

(M.Blank et al., 2005) is deﬁned as

φ(x,y,t) = U (x,y,t)+K

∂

∂x

∂

∂y

∂

∂t

(3)

Figure 6: 8-Level segmentation of sample frames of the

space time shape of the “Jumping-Jack” action.

where U(x, y,t) is the distance transformed space time

shape, K

is the weight added to the derivative taken

along the i

axis. The weights associated with the

Figure 6: 8-Level segmentation of sample frames of the

space time shape of the “Jumping-Jack” action.

where U(x,y,t) is the distance transformed space time

shape, K

is the weight added to the derivative taken

along the i

axis. The weights associated with the

gradients along each of the axes are usually kept the

same. It is seen that the proper variation occurs where

the time axis has more emphasis. The fast moving

parts in this case being the hands and legs have high

values, the region surrounding the torso which are not

so fast moving have moderate values while the torso

region which moves very slowly with respect to the

limbs have very low values. Moreover this represen-

tation also contains concatenation of silhouettes from

the previous frame onto the current frame due to the

ACTION RECOGNITION BASED ON MULTI-LEVEL REPRESENTATION OF 3D SHAPE

381

gradient and so, the time nature is emphasized in a

single frame of the space time shape. In short, this

representation of the space time shape is tuned more

towards the time variation where this variation is di-

rectly related to the action being performed. The nor-

malized gradient L(x,y,t) is given by

L(x,y,t) =

log(φ(x, y,t))

max

(x,y,t)ε S

(φ(x,y,t))

(4)

gradients along each of the axes are usually kept the

same. It is seen that the proper variation occurs where

the time axis has more emphasis. The fast moving

parts in this case being the hands and legs have high

values, the region surrounding the torso which are not

so fast moving have moderate values while the torso

region which moves very slowly with respect to the

limbs have very low values. Moreover this represen-

tation also contains concatenation of silhouettes from

the previous frame onto the current frame due to the

gradient and so, the time nature is emphasized in a

single frame of the space time shape. In short, this

representation of the space time shape is tuned more

towards the time variation where this variation is di-

rectly related to the action being performed. The nor-

malized gradient L(x,y,t) is given by

L(x,y,t) =

log(φ(x,y,t))

max

(x,y,t)εS

(φ(x,y,t))

(4)

Figure 7: R-Transform Feature Set of the jumping jack and

the walk actions at a ﬁnest level.

This normalized gradient is used to segment the

space time shape into multiple levels where at each

level, the features corresponding to the silhouette

variations in a frame are extracted. The standard

deviation of L(x,y,t) is computed to deﬁne the in-

Figure 8: R-Translation vector set of the jumping jack and

the walk actions at the coarsest level.

terval between adjacent levels. The interval is de-

ﬁned by s = StdDev/Scale where StdDev is the stan-

dard deviation and Scale is the factor which is usu-

ally taken as 4. The minimum value is taken to be

zero and the threshold for each level is computed as

T h = (p − 1) × s where p refers to the level. For a K

level segmentation, p varies from 1 to K. An illustra-

tion of 8-level segmentation of a space time shape for

different frames are shown in Figure 6. The segmen-

tation is done on each frame using the values of the

normalized gradient and from each level, a particular

set of features are extracted. In the next section, the

type of features extracted from the space time shape

will be discussed.

4.4 Extraction of Features

There are two sets of features which are extracted

from the segmented space time shape. One is the set

of translation invariant R-Transform features obtained

at each level and the other is the R-Translation vectors

which are extracted at the coarsest level of the space

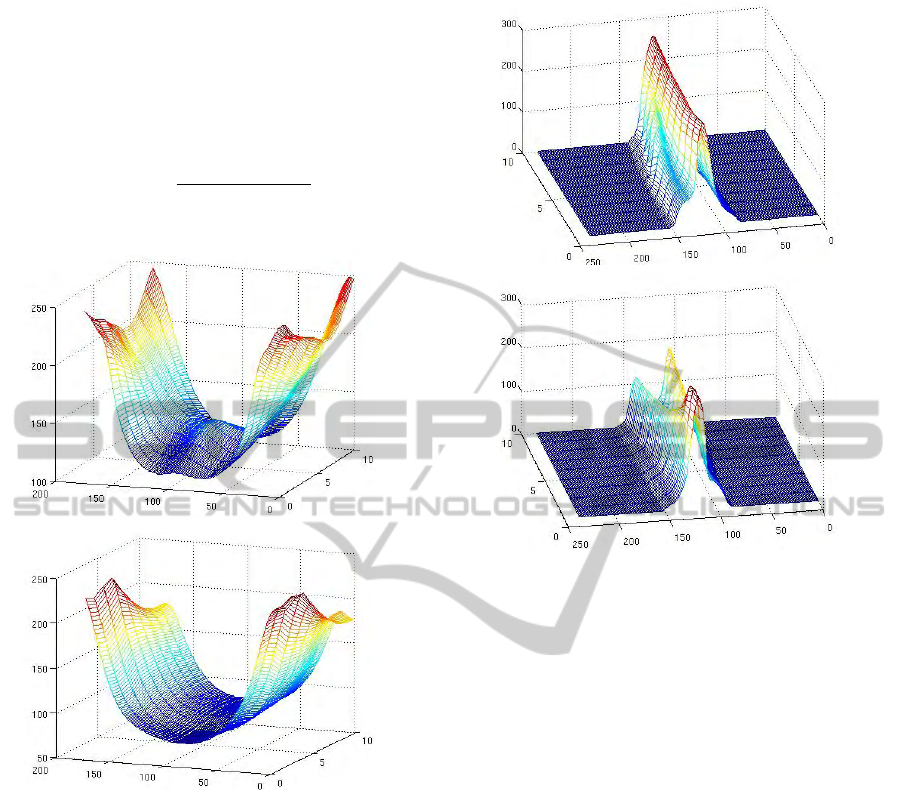
time shape. The R-Transform describes the 2D shape

in a frame at a certain level. The set of R-Transforms

taken across the frames of the space time shape at

Figure 7: R-Transform Feature Set of the jumping jack and

the walk actions at a ﬁnest level.

This normalized gradient is used to segment the

space time shape into multiple levels where at each

level, the features corresponding to the silhouette

variations in a frame are extracted. The standard

deviation of L(x, y,t) is computed to deﬁne the in-

terval between adjacent levels. The interval is de-

ﬁned by s = StdDev/Scale where StdDev is the stan-

dard deviation and Scale is the factor which is usu-

ally taken as 4. The minimum value is taken to be

zero and the threshold for each level is computed as

T h = (p − 1) × s where p refers to the level. For a K

level segmentation, p varies from 1 to K. An illustra-

tion of 8-level segmentation of a space time shape for

different frames are shown in Figure 6. The segmen-

tation is done on each frame using the values of the

normalized gradient and from each level, a particular

set of features are extracted. In the next section, the

gradients along each of the axes are usually kept the

same. It is seen that the proper variation occurs where

the time axis has more emphasis. The fast moving

parts in this case being the hands and legs have high

values, the region surrounding the torso which are not

so fast moving have moderate values while the torso

region which moves very slowly with respect to the

limbs have very low values. Moreover this represen-

tation also contains concatenation of silhouettes from

the previous frame onto the current frame due to the

gradient and so, the time nature is emphasized in a

single frame of the space time shape. In short, this

representation of the space time shape is tuned more

towards the time variation where this variation is di-

rectly related to the action being performed. The nor-

malized gradient L(x,y,t) is given by

L(x,y,t) =

log(φ(x,y,t))

max

(x,y,t)ε S

(φ(x,y,t))

(4)

Figure 7: R-Transform Feature Set of the jumping jack and

the walk actions at a ﬁnest level.

This normalized gradient is used to segment the

space time shape into multiple levels where at each

level, the features corresponding to the silhouette

variations in a frame are extracted. The standard

deviation of L(x,y,t) is computed to deﬁne the in-

Figure 8: R-Translation vector set of the jumping jack and

the walk actions at the coarsest level.

terval between adjacent levels. The interval is de-

ﬁned by s = StdDev/Scale where StdDev is the stan-

dard deviation and Scale is the factor which is usu-

ally taken as 4. The minimum value is taken to be

zero and the threshold for each level is computed as

T h = (p − 1) × s where p refers to the level. For a K

level segmentation, p varies from 1 to K. An illustra-

tion of 8-level segmentation of a space time shape for

different frames are shown in Figure 6. The segmen-

tation is done on each frame using the values of the

normalized gradient and from each level, a particular

set of features are extracted. In the next section, the

type of features extracted from the space time shape

will be discussed.

4.4 Extraction of Features

There are two sets of features which are extracted

from the segmented space time shape. One is the set

of translation invariant R-Transform features obtained

at each level and the other is the R-Translation vectors

which are extracted at the coarsest level of the space

time shape. The R-Transform describes the 2D shape

in a frame at a certain level. The set of R-Transforms

taken across the frames of the space time shape at

Figure 8: R-Translation vector set of the jumping jack and

the walk actions at the coarsest level.

type of features extracted from the space time shape

will be discussed.

4.4 Extraction of Features

There are two sets of features which are extracted

from the segmented space time shape. One is the set

of translation invariant R-Transform features obtained

at each level and the other is the R-Translation vectors

which are extracted at the coarsest level of the space

time shape. The R-Transform describes the 2D shape

in a frame at a certain level. The set of R-Transforms

taken across the frames of the space time shape at

each level gives the posture variations corresponding

to a particular action. The R-Translation vector taken

at the coarsest level emphasizes the translatory vari-

ation of the entire silhouette across the frames of the

space time shape while reducing the emphasis on the

posture variations.

4.4.1 R-Transform Feature Set

The R-Transform feature set is the set of elements

where each element is given by

k,l

(α) =

∞

−∞

k,l

(s,α)ds (5)

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

382

where T

k,l

(s,α) is the 2D Radon transform of the

frame k of the space time shape at level l and αε [0, π[

is the angle of inclination of the line on which the sil-

houette in the frame is projected on (S. Tabbone et al.,

2006). For a space time shape containing K frames

and for L number of levels, the R-Transform feature

set is a 3D matrix of size L × M × K where M is the

number of angles on which the projection is taken.

Typically, M is taken as 180. The surface plot for the

R-Transform feature set for a single level is shown in

Figure 7. This gives the posture variations of the sil-

houette across the frames and these differ from action

to action and are independent of the person perform-

ing it. This is due to the fact that the R-Transform is

scale and translation invariant where scale invariance

removes the size variations in the persons performing

the action and the variations captured are only due to

the change of shape. Moreover, being translation in-

variant, the features are also independent of the posi-

tion of the person performing the action.

4.4.2 R-Translation Vector Set

The R-Transform feature set gives the variations of

the silhouette shape across the frames but removes the

variation caused due to the translation of the shape.

Therefore, to distinguish between the actions which

have large translatory motions such as walk and run

actions from those which have very little translatory

motion such as single hand wave action, another set

of features should be extracted which gives the trans-

latory variation while minimizing the time variation

of the shape. This type of feature is known as the

R-Translation vector shown in Figure 8. This fea-

ture vector extracted from a frame k of the space time

shape at the coarsest level, is given by

(s) =

−π

k,1

(s,α)dα (6)

where T

k,l

is the 2D Radon transform of the centered

silhouette present at the frame k. The R-translation

vector is obtained by integrating the 2D Radon trans-

form over the variable α. Before the extraction of

the R-Translation vector, the silhouette in every frame

of the space time shape is shifted with respect to the

position of the silhouette in the ﬁrst frame. The R-

Translation vector is then extracted from the modi-

ﬁed silhouettes and the variation in this vector across

the frames gives the translation of the silhouette. The

set of R-Translation vectors extracted from the space

time shape is a matrix of size K × M where K is the

number of frames and M refers to twice the maxi-

mum distance of the projection line from the centroid

of the silhouette. At every frame k, Figure 8 shows

a Gaussian-like function having a peak at s = M/2

and these Gaussian-like functions do not vary much

across the frames for the jumping jack action but for

the walk action, there is considerable variation. This

shows that the jumping jack action has less transla-

tory motion than the walk action. The small variations

that occur in the R-Translation vectors of the jumping

jack is due to the posture variations but unlike the R-

Transform feature set, the type of variations have less

emphasis in the R-Translation vector.

5 SIMULATION AND RESULTS

The implementation of the algorithm are done using

MATLAB and OPENCV library by calling the nec-

essary functions. The extraction of the silhouettes

is done in C++ using OPENCV (G. Bradski and A.

Kaehler, 2008) while the rest of the algorithm such as

the extraction of R-Translation and R-Transform fea-

tures is done in the MATLAB environment. The train-

ing and the testing is done using the Weizmann action

dataset which consists of 90 low-resolution video se-

quences each having a single person performing a par-

ticular action. Each video sequence is taken at 50 fps

with a frame size of 180 × 144 and the dataset con-

tains 10 different action classes. Space time shapes

are extraced from each of the video sequences by us-

ing a window along the time axis where this win-

dow is of a pre-deﬁned length. The training and

the testing data set thus consists of the space time

shapes extracted from each of the video sequences

in the database. For evaluation of the algorithm, a

variation of the “leave-one-out” procedure (M. Blank

et al., 2005) is used where to test a video sequence,

the space time shapes corresponding to that particu-

lar video sequence is taken as the testing data while

the training data set is the set of space time shapes

extracted from the sequences excluding the test se-

quence. Classiﬁcation of the test set is done by tak-

ing each test space time shape independently and by

comparing the features extracted from it with those

extracted from the training space time shapes, the in-

dividual test space time shape is classiﬁed. The com-

parison is done using the nearest neighbour rule (C.

M. Bishop, 2006) by computing the Euclidean dis-

tance between the features. Once the closest training

space time shape is identiﬁed, its class is noted and

the test space time shape is classiﬁed under this par-

ticular class. The number of test space time shapes

classiﬁed correctly for each class are noted and this is

put up in the form of the confusion matrix. The con-

fusion matrix showing the action recognition rates for

the proposed algorithm are shown in Table 1.

The algorithm is also shown to be somewhat con-

ACTION RECOGNITION BASED ON MULTI-LEVEL REPRESENTATION OF 3D SHAPE

383

sistent with the change in the window size used for ex-

tracting the space time shape and the overlap between

consecutive shapes. Simulations were done with 6

different sets of (length,overlap) of space time shape

- (6,3), (8,4), (10,5), (12,6) ,(14,7) and (16,8) and the

recognition rates for each action achieved with each

of the sets is shown in Figure 10. By performing the

evaluation with different sets of the window size and

overlap, we are inturn evaluating the variation caused

due to the speed of the action. If we assume that for

a space time shape, we have a ﬁxed start frame, then,

by varying the window size, the end frames will dif-

fer. This is the same effect as capturing the same ac-

tion with the same window size but both actions per-

formed at two different speeds. As mentioned before,

there is not much variation in the action accuracies for

each action except the case of the skip where the ac-

curacy drops to a slightly lower value. As long as the

variation in the speed of the action is within a certain

limit, the algorithm is consistent with the recognition

accuracy.

It can be seen that the accuracy for each action

is fairly good enough at around 90 − 95 % with some

actions having an average accuracy of 88 %. But one

particular action, the “skip” action gets an accuracy

of around 60 − 65 %. The impact of this action when

computing the overall accuracy achieved with this al-

gorithm is shown in Figure 9.

Table 1: Confusion Matrix for the Proposed Algorithm. a1

- bend, a2 - jump in place , a3 - jumping jack , a4 - jump

forward , a5 - run , a6 - side , a7 - single-hand wave , a8 -

skip , a9 - double-hand wave , a10 - walk.

a1 a2 a3 a4 a5 a6 a7 a8 a9 a10

a1 100

a2 100

a3 96 3

a4 88 11

a5 86 10 4

a6 96 3

a7 2 97

a8 3 15 65 15

a9 4 1 94

a10 2 1 1 93

It is seen that without including the skip action,

the algorithm achieves a very good overall accu-

racy of around 93 − 95 % accuracy. The inclusion

of the “skip” action reduces the overall accuracy to

90 − 93 %. But even with the “skip” action, the over-

all accuracy is fairly good enough. This reason for

the “skip” action to have a poor accuracy when com-

pared to other actions is due to the fact that some of

the “skip” space time shapes are qualitatively similar

to the “walk” and “run” space time shapes and thus,

they get misclassiﬁed under the “walk” and “run” ac-

Table 2: Confusion Matrix for Algorithm using Poisson’s

equation based shape descriptor.a1 - bend, a2 - jump in

place , a3 - jumping jack , a4 - jump forward , a5 - run ,

a6 - side , a7 - single-hand wave , a8 - skip , a9 - double-

hand wave , a10 - walk.

a1 a2 a3 a4 a5 a6 a7 a8 a9 a10

a1 99

a2 100

a3 100

a4 89

a5 98

a6 100

a7 94

a8 97

a9 97

a10 100

comparing the features extracted from it with those

extracted from the training space time shapes, the

individual test space time shape is classiﬁed. The

comparison is done using the nearest neighbour rule

(C.M.Bishop, 2006) by computing the Euclidean dis-

tance between the features. Once the closest training

space time shape is identiﬁed, its class is noted and

the test space time shape is classiﬁed under this par-

ticular class. The number of test space time shapes

classiﬁed correctly for each class are noted and this is

put up in the form of the confusion matrix. The con-

fusion matrix showing the action recognition rates for

the proposed algorithm are shown in Table 1.

The algorithm is also shown to be somewhat con-

sistent with the change in the window size used for ex-

tracting the space time shape and the overlap between

consecutive shapes. Simulations were done with 6

different sets of (length,overlap) of space time shape

- (6,3), (8,4), (10,5), (12,6) ,(14,7) and (16,8) and the

recognition rates for each action achieved with each

of the sets is shown in Figure 10. By performing the

evaluation with different sets of the window size and

overlap, we are inturn evaluating the variation caused

due to the speed of the action. If we assume that for

a space time shape, we have a ﬁxed start frame, then,

by varying the window size, the end frames will dif-

fer. This is the same effect as capturing the same ac-

tion with the same window size but both actions per-

formed at two different speeds. As mentioned before,

there is not much variation in the action accuracies for

each action except the case of the skip where the ac-

curacy drops to a slightly lower value. As long as the

variation in the speed of the action is within a certain

limit, the algorithm is consistent with the recognition

accuracy.

It can be seen that the accuracy for each action

is fairly good enough at around 90 − 95 % with some

actions having an average accuracy of 88 %. But one

particular action, the “skip” action gets an accuracy

of around 60 − 65 %. The impact of this action when

computing the overall accuracy achieved with this al-

gorithm is shown in Figure 9.

It is seen that without including the skip action,

the algorithm achieves a very good overall accu-

racy of around 93 − 95 % accuracy. The inclusion

of the “skip” action reduces the overall accuracy to

90 − 93 %. But even with the “skip” action, the over-

all accuracy is fairly good enough. This reason for

the “skip” action to have a poor accuracy when com-

pared to other actions is due to the fact that some of

the “skip” space time shapes are qualitatively similar

to the “walk” and “run” space time shapes and thus,

they get misclassiﬁed under the “walk” and “run” ac-

tions. The features extracted capture the more global

Table 1: Confusion Matrix for the Proposed Algorithm. a1

- bend, a2 - jump in place , a3 - jumping jack , a4 - jump

forward , a5 - run , a6 - side , a7 - single-hand wave , a8 -

skip , a9 - double-hand wave , a10 - walk.

a1 a2 a3 a4 a5 a6 a7 a8 a9 a10

a1 100

a2 100

a3 96 3

a4 88 11

a5 86 10 4

a6 96 3

a7 2 97

a8 3 15 65 15

a9 4 1 94

a10 2 1 1 93

Table 2: Confusion Matrix for Algorithm using Poisson’s

equation based shape descriptor.a1 - bend, a2 - jump in

place , a3 - jumping jack , a4 - jump forward , a5 - run ,

a6 - side , a7 - single-hand wave , a8 - skip , a9 - double-

hand wave , a10 - walk.

a1 a2 a3 a4 a5 a6 a7 a8 a9 a10

a1 99

a2 100

a3 100

a4 89

a5 98

a6 100

a7 94

a8 97

a9 97

a10 100

Figure 9: The overall accuracy acheived with and with-

out including the skip action for different space time shape

lengths.

variations of a space time shape and are not able to

fully distinguish between the variations in the “skip”

to that of the “walk” and “run” space time shapes.

One possible way of improving the distinguishability

of these features is to extract another subset of fea-

tures which are more localised and which can provide

more discrimination between the space time shapes.

The confusion matrices for the algorithm which

use the poisson equation’s based shape descriptor is

Figure 9: The overall accuracy acheived with and with-

out including the skip action for different space time shape

lengths.

Figure 10: Accuracy for each action acheived with the dif-

ferent lengths of space time shape. The overlap is half the

length of the space time shape.

Figure 11: Comparison of overall accuracies acheived the

different shape descriptors used in the proposed action

recognition framework without including the “skip” action.

given in Table 2. As seen, the algorithm using the

Poisson’s equation based shape descriptor gives bet-

ter accuracy results for some actions especially the

“skip” action. This is because the features extracted

are localized within the space time shape and thus

are able to fully distinguish between the “skip” and

“walk” shapes. But, the proposed algorithm attains

comparable results with the other actions some ac-

tions attaining better accuracy with the proposed one.

When compared to other shape descriptors, the pro-

posed algorithm uses a combination of shape descrip-

tors which brings out more time variations relating

to the action . This is illustrated in where the shape

descriptor used in the proposed algorithm is com-

pared with other shape descriptors. As shown, the

shape descriptor used in the proposed action recogni-

tion framework has much better overall accuracy than

when acheived with using only the 2D shape descrip-

tors to capture the posture variations.

6 CONCLUSIONS

The algorithm proposed in this paper have used the

concept of a multi-level representation of a 3D shape

for action classiﬁcation. An action has been consid-

ered as a space time shape or a 3D shape and a multi-

level representation using the gradient of the 3D Eu-

clidean distance transform and the Radon transform

have been used from where the action features have

been extracted. Silhouettes from a video sequence

containing a particular action have been concante-

nated to form the space time shape representing that

action. Action features were extracted from each level

of the representation and these features concatenated

as a single feature was used in a nearest neighbour

classiﬁer for recognition.

The evaluation of the algorithm was performed

by comparing the accuracies attained with different

shape descriptors in the proposed algorithm and the

results obtained showed higher accuracy rates for the

combination of the shape descriptors. Furthur com-

parison has been done with another algorithm pro-

posed in (M.Blank et al., 2005) and the results showed

comparable recognition accuracies for some actions

with some actions having better accuracies with the

proposed one. The accuracies were also computed

for different shape time shape lengths and overlap and

showed that the algorithm was almost consistent with

the variation in the length of the space time shape.

However, the algorithm has not been evaluated for the

variation in the accuracy of a particular action due to

the change in the frame rate as the database used for

evaluation is limited and contains only sequences cap-

tured at a constant frame rate.

Although the average accuracies were high, the

accuracy for one particular action obtained by the pro-

posed algorithm is low as the features extracted from

the space time shape corresponding to this action can-

not be discriminated from those of similar actions.

Future work will involve extraction of weights from

the action features which corresponds to its variation

and then, use a learning based methodolgy to classify

them.

REFERENCES

A.A.Efros, A.C.Berg, G.Mori, and J.Malik (2003). Recog-

nizing action at a distance. In Proceedings of Ninth

IEEE International Conference on Computer Vision.

A.Khotanzad and Y.H.Hong (1990). Invariant image recog-

nition by zernike moments. In IEEE Transactions on

Pattern Analysis and Machine Intelligence.

A.Mohiuddin and S.W.Lee (2008). Human action recogni-

Figure 10: Accuracy for each action acheived with the dif-

ferent lengths of space time shape. The overlap is half the

length of the space time shape.

tions. The features extracted capture the more global

variations of a space time shape and are not able to

fully distinguish between the variations in the “skip”

to that of the “walk” and “run” space time shapes.

One possible way of improving the distinguishability

of these features is to extract another subset of fea-

tures which are more localised and which can provide

more discrimination between the space time shapes.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

384

Figure 10: Accuracy for each action acheived with the dif-

ferent lengths of space time shape. The overlap is half the

length of the space time shape.

Figure 11: Comparison of overall accuracies acheived the

different shape descriptors used in the proposed action

recognition framework without including the “skip” action.

given in Table 2. As seen, the algorithm using the

Poisson’s equation based shape descriptor gives bet-

ter accuracy results for some actions especially the

“skip” action. This is because the features extracted

are localized within the space time shape and thus

are able to fully distinguish between the “skip” and

“walk” shapes. But, the proposed algorithm attains

comparable results with the other actions some ac-

tions attaining better accuracy with the proposed one.

When compared to other shape descriptors, the pro-

posed algorithm uses a combination of shape descrip-

tors which brings out more time variations relating

to the action . This is illustrated in where the shape

descriptor used in the proposed algorithm is com-

pared with other shape descriptors. As shown, the

shape descriptor used in the proposed action recogni-

tion framework has much better overall accuracy than

when acheived with using only the 2D shape descrip-

tors to capture the posture variations.

6 CONCLUSIONS

The algorithm proposed in this paper have used the

concept of a multi-level representation of a 3D shape

for action classiﬁcation. An action has been consid-

ered as a space time shape or a 3D shape and a multi-

level representation using the gradient of the 3D Eu-

clidean distance transform and the Radon transform

have been used from where the action features have

been extracted. Silhouettes from a video sequence

containing a particular action have been concante-

nated to form the space time shape representing that

action. Action features were extracted from each level

of the representation and these features concatenated

as a single feature was used in a nearest neighbour

classiﬁer for recognition.

The evaluation of the algorithm was performed

by comparing the accuracies attained with different

shape descriptors in the proposed algorithm and the

results obtained showed higher accuracy rates for the

combination of the shape descriptors. Furthur com-

parison has been done with another algorithm pro-

posed in (M.Blank et al., 2005) and the results showed

comparable recognition accuracies for some actions

with some actions having better accuracies with the

proposed one. The accuracies were also computed

for different shape time shape lengths and overlap and

showed that the algorithm was almost consistent with

the variation in the length of the space time shape.

However, the algorithm has not been evaluated for the

variation in the accuracy of a particular action due to

the change in the frame rate as the database used for

evaluation is limited and contains only sequences cap-

tured at a constant frame rate.

Although the average accuracies were high, the

accuracy for one particular action obtained by the pro-

posed algorithm is low as the features extracted from

the space time shape corresponding to this action can-

not be discriminated from those of similar actions.

Future work will involve extraction of weights from

the action features which corresponds to its variation

and then, use a learning based methodolgy to classify

them.

REFERENCES

A.A.Efros, A.C.Berg, G.Mori, and J.Malik (2003). Recog-

nizing action at a distance. In Proceedings of Ninth

IEEE International Conference on Computer Vision.

A.Khotanzad and Y.H.Hong (1990). Invariant image recog-

nition by zernike moments. In IEEE Transactions on

Pattern Analysis and Machine Intelligence.

A.Mohiuddin and S.W.Lee (2008). Human action recogni-

Figure 11: Comparison of overall accuracies acheived the

different shape descriptors used in the proposed action

recognition framework without including the “skip” action.

The confusion matrices for the algorithm which

use the poisson equation’s based shape descriptor is

given in Table 2. As seen, the algorithm using the

Poisson’s equation based shape descriptor gives bet-

ter accuracy results for some actions especially the

“skip” action. This is because the features extracted

are localized within the space time shape and thus

are able to fully distinguish between the “skip” and

“walk” shapes. But, the proposed algorithm attains

comparable results with the other actions some ac-

tions attaining better accuracy with the proposed one.

When compared to other shape descriptors, the pro-

posed algorithm uses a combination of shape descrip-

tors which brings out more time variations relating

to the action . This is illustrated in where the shape

descriptor used in the proposed algorithm is com-

pared with other shape descriptors. As shown, the

shape descriptor used in the proposed action recogni-

tion framework has much better overall accuracy than

when acheived with using only the 2D shape descrip-

tors to capture the posture variations.

6 CONCLUSIONS

The algorithm proposed in this paper have used the

concept of a multi-level representation of a 3D shape

for action classiﬁcation. An action has been consid-

ered as a space time shape or a 3D shape and a multi-

level representation using the gradient of the 3D Eu-

clidean distance transform and the Radon transform

have been used from where the action features have

been extracted. Silhouettes from a video sequence

containing a particular action have been concante-

nated to form the space time shape representing that

action. Action features were extracted from each level

of the representation and these features concatenated

as a single feature was used in a nearest neighbour

classiﬁer for recognition.

The evaluation of the algorithm was performed

by comparing the accuracies attained with different

shape descriptors in the proposed algorithm and the

results obtained showed higher accuracy rates for the

combination of the shape descriptors. Furthur com-

parison has been done with another algorithm pro-

posed in (M. Blank et al., 2005) and the results

showed comparable recognition accuracies for some

actions with some actions having better accuracies

with the proposed one. The accuracies were also com-

puted for different shape time shape lengths and over-

lap and showed that the algorithm was almost consis-

tent with the variation in the length of the space time

shape. However, the algorithm has not been evaluated

for the variation in the accuracy of a particular action

due to the change in the frame rate as the database

used for evaluation is limited and contains only se-

quences captured at a constant frame rate.

Although the average accuracies were high, the

accuracy for one particular action obtained by the pro-

posed algorithm is low as the features extracted from

the space time shape corresponding to this action can-

not be discriminated from those of similar actions.

Future work will involve extraction of weights from

the action features which corresponds to its variation

and then, use a learning based methodolgy to classify

them.

REFERENCES

A. A. Efros, A. C. Berg, G. Mori and J.Malik (2003). Rec-

ognizing action at a distance. In Proceedings of Ninth

IEEE International Conference on Computer Vision.

A. Khotanzad and Y. H. Hong (1990). Invariant image

recognition by zernike moments. In IEEE Transac-

tions on Pattern Analysis and Machine Intelligence.

A. Mohiuddin and S. W. Lee (2008). Human action recogni-

tion using shape and clg-motion ﬂow from multi-view

image sequences. In Pattern Recognition.

A. Rosenfeld and J. Pfaltz (1966). Sequential operations in

digital picture processing. In Journal of the Associa-

tion for Computing Machinery.

C. J. Cohen, K. A. Scott, M. J. Huber, S. C. Rowe and F.

Morelli (2008). Behavior recognition architecture for

surveillance applications. In International Workshop

on Applied Imagery and Pattern Recognition - AIPR

2008.

C. M. Bishop (2006). Pattern Recognition and Machine

Learning. Springer.

D. Batra, T. Chen, and R. Sukthankar (2008). Space-time

shapelets for action recognition. In IEEE Workshop

on Motion and Video Computing - WMVC 2008.

ACTION RECOGNITION BASED ON MULTI-LEVEL REPRESENTATION OF 3D SHAPE

385

D. W. Paglieroni (1992). Distance transforms: Properties

and machine vision applications. In Graphical Models

and Image Processing - CVGIP 1992.

D. Zhang and G. Lu (2003). A comparative study on shape

retrieval using fourier descriptors with different shape

signatures. In Journal of Visual Communication and

Image Representation.

G. Borgefors (1984). Distance transformations in arbitrary

dimensions. In Computer Vision, Graphics, and Im-

age Processing.

G. Bradski and A. Kaehler (2008). Learning OpenCV.

O’Reilly Media Inc.

G. R. Bradski and J. W. Davis (2000). Motion segmentation

and pose recognition with motion history gradients.

In Fifth IEEE Workshop on Applications of Computer

Vision.

J. C. Niebles, H. Wang and L. Fei-Fei (2006). Unsu-

pervised learning of human action categories using

spatial-temporal words. In Proceedings of the British

Machine Vision Conference - BMVC 2006.

J. W. Davis (2003). Hierarchical motion history images

for recognizing human motion. In Proceedings of

the IEEE Workshop on Detection and Recognition of

Events in Video.

J. W. Davis and A. F. Bobick (1997). The representation and

recognition of human movement using temporal tem-

plates. In Proceedings of the IEEE Computer Society

Conference on Computer Vision and Pattern Recogni-

tion.

J.Zhang, K. F. Man and J. Y. Ke (1998). Timeseries pre-

diction using lyapunov exponents in embedding phase

space. In International Conference on Systems, Man

and Cybernetics.

L. Gorelick, M. Galun, E. Sharon, R. Basri, and A. Brandt

(2004). Shape representation and classiﬁcation us-

ing the poisson equation. In Proceedings of the 2004

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition-CVPR 2004.

M. Blank, L. Gorelick, E. Shechtman, M.Irani, and R.Basri

(2005). Actions as space-time shapes. In Tenth IEEE

International Conference on Computer Vision - ICCV

2005.

M. K. Hu (2008). Visual pattern recognition by moment

invariants. In IEEE Workshop on Motion and Video

Computing - WMVC 2008.

M.Mitani, M.Takaya, A.Kojima, and K.Fukunaga (2006).

Environment recognition based on analysis of human

actions for mobile robot. In The 18th International

Conference on Pattern Recognition - ICPR 2006.

P. F. Felzenszwalb and D. P. Huttenlocher (2004). Distance

transforms of sampled functions. In Technical report,

Cornell Computing and Information Science.

P. Scovanner, S. Ali, and M. Shah (2007). A 3-dimensional

sift descriptor and its application to action recognition.

In Proceedings of the 15th ACM International Confer-

ence on Multimedia.

Q. Chen, E. Petriu and X.Yang (2004). A comparative study

of fourier descriptors and hu’s seven moment invari-

ants for image recognition. In Canadian Conference

on Electrical and Computer Engineering.

R. N. Bracewell (1995). Two-Dimensional Imaging. Pren-

tice Hall, Englewood Cliffs, NJ.

S. Ali, A. Basharat and M.Shah (2007). Chaotic invariants

for human action recognition. In IEEE 11th Interna-

tional Conference on Computer Vision - ICCV 2007.

S. Tabbone, L. Wendling and J. P.Salmon (2006). A new

shape descriptor deﬁned on the radon transform. In

Computer Vision and Image Understanding.

X. Sun, M. Chen and A.Hauptmann (2009). Action recog-

nition via local descriptors and holistic features. In

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition Workshops.

Y. Wang, K. Huang and T.Tan (2007). Human activity

recognition based on r-transform. In IEEE Conference

on Computer Vision and Pattern Recognition - CVPR

2007.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

386