BIOLOGICALLY INSPIRED ROBOT NAVIGATION BY

EXPLOITING OPTICAL FLOW PATTERNS

Sotirios Ch. Diamantas

∗

Intelligence, Agents, Multimedia Group, School of Electronics and Computer Science

University of Southampton, Southampton, SO17 1BJ, U.K.

Anastasios Oikonomidis

Centre for Risk Research, School of Management, University of Southampton, Southampton, SO17 1BJ, U.K.

Richard M. Crowder

Intelligence, Agents, Multimedia Group, School of Electronics and Computer Science

University of Southampton, Southampton, SO17 1BJ, U.K.

Keywords:

Optical ﬂow, Biologically inspired robot navigation, Robot homing, Visual navigation, Mobile robotics.

Abstract:

In this paper a novel biologically inspired method is addressed for the robot homing problem where a robot

returns to its home position after having explored an a priori unknown environment. The method exploits

the optical ﬂow patterns of the landmarks and based on a training data set a probability is inferred between

the current snapshot and the snapshots stored in memory. Optical ﬂow, which is not a property of landmarks

like color, shape, and size but a property of the camera motion, is used for navigating a robot back to its home

position. In addition, optical ﬂow is the only information provided to the system while parameters like position

and velocity of the robot are not known. Our method proves to be effective even when the snapshots of the

landmarks have been taken from varying distances and velocities.

1 INTRODUCTION

Recently there has been a resurgence of interest in

biologically inspired robotics. Biology is seen as an

alternative solution to the problems robots encounter

which includes algorithmic complexity, performance,

and power consumption among others. The num-

ber of neurons an insect possess is approximately

while those found in a human brain are between

and 10

. Biological inspiration provides simple,

yet effective methods for the solutions of such prob-

lems. The careful examination of those methods has a

twofold gain. By examining the methods animals em-

ploy we can design better and more efﬁcient robots,

and by building such robots we can understand better

how the mechanisms of animals work as well as how

they have evolved over time.

∗

Currently a postdoctoral research associate within In-

telligent Robot Lab, Pusan National University, Republic

of Korea.

Navigation lies at the heart of mobile robotics.

Homing (or inbound journey) refers to the navigation

process where an autonomous agent performs a return

to its home position after having completed foraging

(or outbound journey; foraging is mainly attributed to

a biological agent). A robot may have to return to its

base for a number of reasons like recharging batter-

ies, failure of a subsystem, or completion of a task.

The application areas of robots capable of performing

homing are plenty and vary. Search and rescue robots

are in need in areas that have been hit by earthquakes

or in environments which are hazardous for humans

(Matsuno and Tadokoro, 2004). Planetary missions

to other regions constitute another application area

of robots whose navigation process involves returning

back to their base. In this paper we have developed a

novel approach to tackle the problem of robot homing

using visual modality as the only source of informa-

tion. No other sensor is provided to the robotic agent

apart from two side cameras mounted on a simulated

645

Ch. Diamantas S., Oikonomidis A. and M. Crowder R..

BIOLOGICALLY INSPIRED ROBOT NAVIGATION BY EXPLOITING OPTICAL FLOW PATTERNS.

DOI: 10.5220/0003377706450652

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 645-652

ISBN: 978-989-8425-47-8

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

mobile platform.

Optical ﬂow, that is the rate of change of image

motion in the retina or a visual sensor, is extracted

from the motion of an autonomous agent. The orien-

tation of the cameras on the robotic platform is per-

pendicular to the direction of motion so as a transla-

tional optical ﬂow information is generated. Optical

ﬂow, which is not a property of the landmarks, like

color, shape, and size, but of the camera motion has

been used for building topological maps in a priori

unknown environment based on the optical ﬂow pat-

terns of the landmarks. The novelty of our method

lies in the fact that no information is given such as

the position or the velocity of the robot but only the

optical ﬂow ‘ﬁngerprint’ of the landmarks caused by

the motion of the robot. For this purpose, a train-

ing algorithm has been deployed and a probability is

inferred that is computed from the similarity of the

optical ﬂow patterns between the maps built during

the outbound and inbound trip. The work in this pa-

per builds upon the work of (Diamantas et al., 2010)

that also appears by (Diamantas, 2010) where a single

vector was modeled at varying distances and veloci-

ties. In the current work, the optical ﬂow pattern of a

landmark is modeled and its variation at varying dis-

tances and velocities is observed.

This paper is comprised of ﬁve sections. Follow-

ing is Section 2 where related work is presented. In

Section 3 the methodology of the homing model is de-

scribed. Section 4 presents the results of the statistical

model on the homing process of navigation. Finally,

Section 5 epitomizes the paper with a brief discussion

on the conclusions drawn from this work.

2 RELATED WORK

A large number of insects use optic ﬂow for navi-

gation. Insects like Drosophila use the apparent vi-

sual motion of objects to supply information about

the three-dimensional structure of the environment.

The ﬂy Drosophila uses optic ﬂow to pick near tar-

gets. (Collett, 2002) shows that the task of evaluat-

ing distances between objects is made easier by mak-

ing side-to-side movements of the head strictly trans-

lational and disregarding any rotational components

that can inﬂuence the distance to the objects. Loom-

ing, i.e., image expansion, can also distort the actual

distance to the object as the apparent size compared

to the physical size of the object differs. In his exper-

iments (Collett, 2002) ascertains that Drosophila like

many insects limit rotational ﬂow during exploratory

locomotion. In fact, Drosophila move in straight-line

segments and restrict any rotation to saccades at the

end of each segment. (Schuster et al., 2002) have used

virtual reality techniques to show that fruit ﬂies use

translational motion for picking up the nearest object

while disregarding looming.

Ladybirds also move in straight-line segments and

rely on translational optic ﬂow rather that looming

cues. Other animals like locusts and mantids turn

their head from one side to the other just before jump-

ing. (Kral and Poteser, 1997) suggest that locusts and

mantids use translational motion to infer the three-

dimensional structure of the environment and in par-

ticular the distance to the object they wish to ap-

proach. In some other experiments performed by

(Tautz et al., 2004) trained bees had to travel large dis-

tances across various scenes that included both land

and water. The results showed that the ﬂights over

water had a signiﬁcantly ﬂatter slope than the ones

above land. This suggests that the perception of the

distance covered by bees is not absolute but scene-

dependent where the optic ﬂow perceived is evidently

larger. This may also suggest why some bees are

drowning by ‘diving’ into lakes or the sea while ﬂy-

ing above water. The distance and direction to a food

source is communicated in the bees by means of wag-

gle dances that integrate retinal image ﬂow along the

ﬂight path (Esch et al., 2001), (von Frisch, 1993).

Experiments conducted by (Hafner, 2004) have

shown that in principle visual homing strategies can

be both learnt and evolved by artiﬁcial agents. Even

a sparse topological representation of place cells can

lead to good spatial representation of the environment

where metric information can easily be extracted, if

required, by the agent. Nevertheless, it is not clear

which navigation strategy is applied by an animal,

since its behavior consists of a combination of dif-

ferent strategies. When, and to what extent, the dif-

ferent strategies are chosen and which sensory modal-

ities are applied is still an open question. Two well-

known homing models are the snapshot and the Av-

erage Landmark Vector (ALV) model. The snapshot

model is an implementation of the template hypoth-

esis (Cartwright and Collett, 1983; Cartwright and

Collett, 1987). It requires a panoramic snapshot of

the goal position, be it a hive, nest, or a food source.

Along with the snapshot the compass direction is

stored. The snapshot model is an image matching pro-

cess between a snapshot taken at a goal position and a

snapshot containing the current view. The image ob-

tained from the omnidirectional camera is unwrapped

and a threshold operation is performed to yield a one-

dimensional black and white image. The landmarks

are denoted as black marks on the image. Then, this

is compared with the snapshot of the current view

to produce the homing vector. The homing vector is

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

646

a two-dimensional vector pointing towards the home

position, and is obtained by summing up all radial and

tangential vector components.

The ALV model developed by (Lambrinos et al.,

2000) uses, too, a processed panoramic image but, in

contrast to the snapshot model, it need not be stored.

Only a two-dimensional vector for each landmark

needs to be stored that points to the direction of the

landmark. Matching and unwrapping of the image are

not required, since the calculations are performed on

the basis of vector components. Thus, ALV is more

parsimonious than the snapshot model. Nevertheless,

snapshots in the ALV model have to be captured and

processed to produce a one-dimensional picture, as is

in the snapshot model. An application of a robot with

homing abilities using panoramic vision is demon-

strated by (Argyros et al., 2005).

2.1 Applications of Optical Flow

Lately a growing number of autonomous vehicles

have been built using techniques inspired by insects

and, in particular, optic ﬂow. One of the ﬁrst works

that studied the relation of scene geometry and the

motion of the observer was by (Gibson, 1974). A

large amount of work, however, has been focused on

obstacle avoidance using optical ﬂow (Camus et al.,

1996; Warren and Fajen, 2004; Merrell et al., 2004).

The technique, generally, works by splitting the im-

age (for single camera systems) into left- and right-

hand side. If the summation of vectors of either side

exceeds a given threshold then the vehicle is about

to collide with an object. Similarly, this method has

been used for centering autonomous robots in cor-

ridors or even a canyon (Hrabar et al., 2005) with

the difference that the summation of vectors this time

must be equal in both the left-hand side and the right-

hand side of the image. (Ohnishi and Imiya, 2007)

utilize optical ﬂow for both obstacle avoidance and

corridor navigation. The performance of optical ﬂow

has also been tested in underwater color images by

(Madjidi and Negahdaripour, 2006). (Vardy, 2005)

employs various optical ﬂow techniques that are com-

pared using block matching and differential methods

to tackle homing. In a recent work implemented by

(Kendoul et al., 2009) optic ﬂow is used for fully

autonomous ﬂight control of an aerial vehicle. The

distance travelled in this Unmanned Aerial Vehicle

(UAV) is calculated by integrating the optical ﬂow

over time. A similar work for controlling a small

UAV in conﬁned and cluttered environments has also

been implemented by (Zufferey et al., 2008). (Bar-

ron et al., 1994) discuss the performance of optical

ﬂow techniques. Their comparison is focused on ac-

curacy, reliability and density of the velocity measure-

ments. Other works employ optic ﬂow methods for

depth perception (Simpson, 1993), motion segmenta-

tion (Blackburn and Nguyen, 1995), or estimation of

ego-motion (Frenz and Lappe, 2005).

A similar technique to optical ﬂow developed by

(Langer and Mann, 2003) called optical snow arises

in situations where camera motion occurs in highly

cluttered 3D environments. Such cases involve a pas-

sive observer watching the fall of the snow, hence the

name of the method optical snow. Optical snow has

been inspired by research in animals that inhabit in

highly dense and cluttered environments; such ani-

mals include the rabbit, the cat, and the bird. The

properties of the optical snow are that yields dense

motion parallax with many depth discontinuities oc-

curring in almost all image points. This comes in

contrast to the classical methods that compute opti-

cal ﬂow and presuppose temporal persistence and spa-

tial coherence. (Langer and Mann, 2003) present the

properties of optical snow in the Fourier domain and

investigateits computational problems on motion pro-

cessing.

3 METHODOLOGY

This section is dedicated to the description of the op-

tical ﬂow method. It is described how the optical ﬂow

‘signature’ of the landmarks, that is caused by the per-

ceived motion of the robot in the environment, can be

used to localize the robot during the homing process.

Various landmarks have been modeled and simulated

from which the robot passes through. The simulated

landmarks have geometrical shapes and they are tex-

tured in order to produce large amounts of optic ﬂow

(as is in real environments). In this work we have

employed the Lucas-Kanade (LK) algorithm (Lucas

and Kanade, 1981). In order for the optic ﬂow al-

gorithm to perform well images that have high tex-

ture and contain a multitude of corners are essential.

Such images have strong derivatives and, when two

orthogonal derivatives are observed then this feature

may be unique, and thus, good for tracking. Track-

ing a feature refers to the ability of ﬁnding a fea-

ture of interest from one frame to a subsequent one.

Tracking the motion of an object can give the ﬂow

of the motion of the objects among different frames.

In Lucas-Kanade algorithm corners are more suitable

than edges for tracking as they contain more informa-

tion. For the implementation of the LK algorithm the

(OpenCV, 2008) library has been used.

As mentioned in Section I the simulated robot

consists of two side-ways cameras which are perpen-

BIOLOGICALLY INSPIRED ROBOT NAVIGATION BY EXPLOITING OPTICAL FLOW PATTERNS

647

dicular to the direction of motion. This creates a

translational optic ﬂow as the robot navigates through

the environment. Every landmark in the environment

‘emits’ a number of optic ﬂow vectors that are de-

pendent on the distance between the robot and the

landmark, and the velocity of the robot. One of the

advantages of our method is that the images are only

captured and are not used for storage or comparison.

Comparing and storing only the properties of vectors

between different frames reduces the computational

complexity and the cost of the homing process.

During the outbound trip of the robot the camera

detects and records the optic ﬂow that is generated by

the motion of the vehicle. During that phase the robot

builds a topological map from the optical ﬂow ‘ﬁn-

gerprint’ of the landmarks. After the foraging trip,

has completed, the homing trip is initiated. In the

homing phase, the robot compares the optical ﬂow

patterns it currently perceives with the ones occurred

during the foraging journey. If the similarity score

(i.e., probability) between the two patterns is above

a given threshold, then the robot assumes the current

landmark observed is the same with the landmark oc-

curred during the outbound trip. This information is

then used to localize the robot within the topological

map. The similarity score of the vectors is a proba-

bilistic result of the Euclidean distance of the vectors

between the current image and the image taken during

the outbound journey.

In order for the robot to localize in the environ-

ment using optic ﬂow vectors, a training data set of

n = 1000 observations has been implemented where

the optical ﬂow pattern of a landmark is observed at

varying distances between the robot and the landmark

and at varying velocities. These distances and the ve-

locities chosen to create the training data set approx-

imate the real distributions of velocity and distance

when a robot navigates in an environment. Thus, a

joint probability distribution has been created with

two continuousand independent variables, that is, dis-

tance and velocity, and is expressed by (1),

C,D

(c,d) = f

(d) ∀c,d. (1)

The velocity, C, and the distance variable, D, have

been drawn by two Gaussian distributions with µ =

4,σ = 1 and µ = 11, σ = 3 respectively. The n ob-

servations model the position of the landmark in the

plane under n varying distances and velocities. One

assumption that needs to be met in our method is that

the majority of the vectors comprising a given land-

mark should have the same, or almost the same mag-

nitude. In order to solve the matching problem be-

tween landmarks, the mean (or center) point of ev-

ery vector is taken. Thus, summing up all the mean

points of the vectors and dividing by the number of

vectors, v, that comprise a landmark we end up hav-

ing the mean of the means as shown in (2).

¯x, ¯y =

∑

l=1

(2)

The mean of the means in an optical ﬂow pattern can

be visualized as the center of gravity in a physical sys-

tem. The same process is repeated ntimes where the

center of gravity is observed at varying distances and

velocities as shown in (3). We then compute the Eu-

clidean distances between the center of gravity of all

n observations and the center of gravity of each and

every observation. Equation (4) shows the process of

ﬁnding the Euclidian distances.

∑

k=1

n = 1000 (3)

− ¯x

)

+ (y

− ¯y

)

(4)

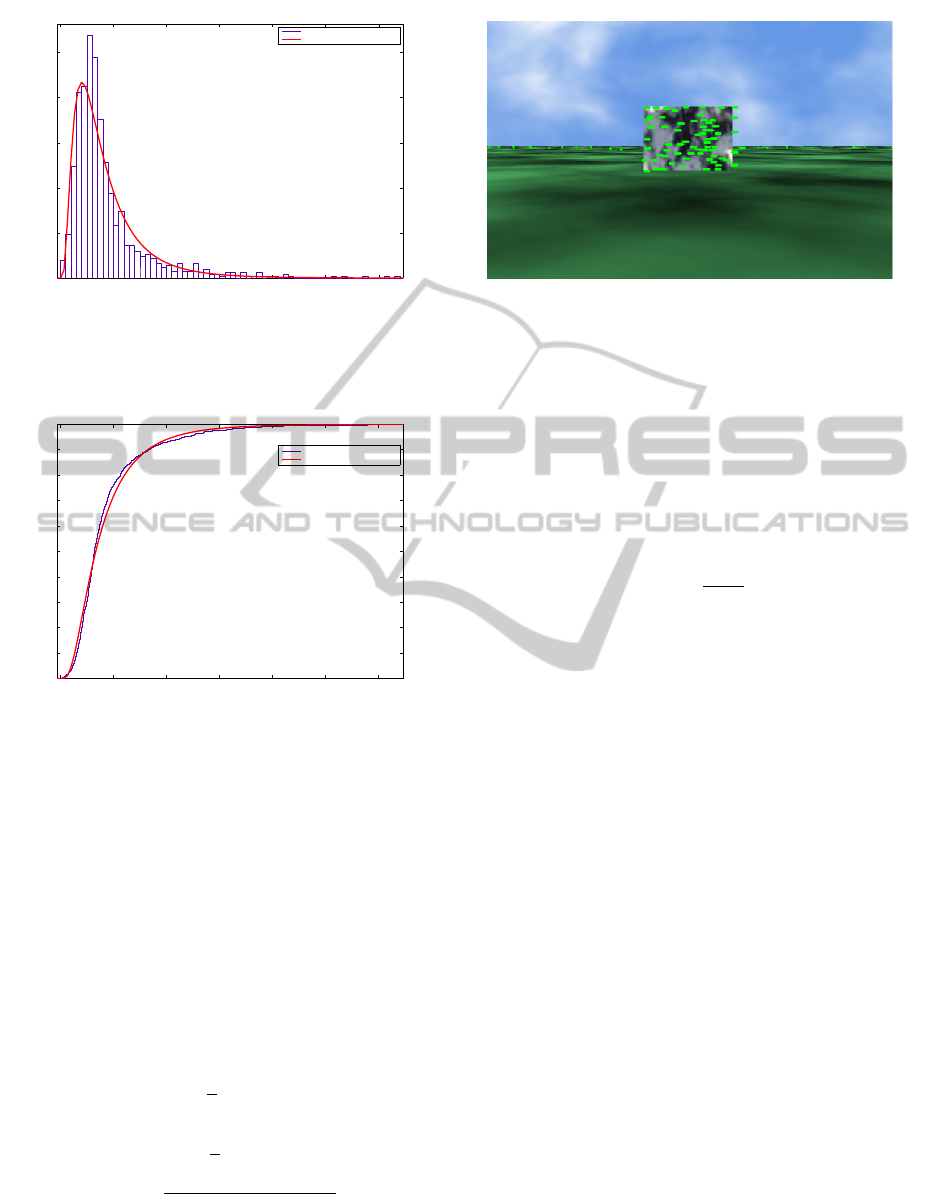
The histogram produced by the Euclidean distances,

, forms a log-normal probability density function

(pdf) with µ = 1.20 and σ = 0.71 in the log-normal

scale. In order to calculate the expected mean, E(µ),

and standard deviation, E(s.d.), the (5) and (6) should

be used, respectively.

E(µ) = e

µ+

(5)

E(s.d.) = e

µ+

−1 (6)

Figure 1 shows the histogram of center of gravity de-

viations and the probability density function of the

log-normal. The log-normal pdf is deployed in order

to infer the probability a match to occur between the

optical ﬂow pattern of the current image and the op-

tical ﬂow pattern stored in memory. Figure 2 depicts

the cumulative distribution function (cdf) of center of

gravity deviations and the log-normal. The probabil-

ity density function of log-normal is given by (7), and

the cumulative density function of log-normal is ex-

pressed by (8), where erfc is the complementary error

function and Φ is the standard normal cdf.

= (δ;µ,σ) =

δσ

√

2π

−

(lnδ−µ)

2σ

δ > 0. (7)

(δ;µ,σ) =

er fc



−

lnδ−µ

√



= Φ



lnδ−µ



(8)

Thus far we have explained the methodology of the

training algorithm. We now move on to the process

of calculating a probability for the patterns observed

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

648

0 5 10 15 20 25 30

0.05

0.1

0.15

0.2

0.25

Data

Density

deviation of mean vector positions

log−normal pdf

Figure 1: Histogram of center of gravity deviations of the

training algorithm and the log-normal probability density

function (pdf) ﬁt. Mean and standard deviation are µ = 1.20

and σ = 0.71 in the log-normal scale, respectively.

0 5 10 15 20 25 30

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Data

Cumulative probability

deviation of mean vector positions

log−normal cdf

Figure 2: Cumulative density functions (cdf) of center of

gravity deviations and the log-normal distribution.

by the robot during the foraging and homing process.

This probability will aid the robot localize itself in the

environment. During the homing navigation process,

the robot calculates the mean of the means (center

of gravity) from every landmark and ﬁnds their Eu-

clidean distance δ with the mean of the means of the

landmarks stored in the database. Equations (9), (10),

and (11) describe the process with two distinct land-

marks. In (9), (10), n and s are the number of vectors

for two distinct landmarks i and j, one of which oc-

curs in the outbound trip while the other one occurs

in the inbound trip.

¯x

, ¯y

∑

a=1

(9)

¯x

, ¯y

∑

b=1

(10)

δ =

( ¯x

− ¯x

)

+ ( ¯y

− ¯y

)

(11)

P = 1−P

(12)

Figure 3: Reference landmark and its optical ﬂow pattern

taken at a distance of 11m and a velocity of 4km/h. This ref-

erence landmark was used for comparison with other land-

marks.

The log-normal cdf then gives us the probability P

based on the Euclidean distance δ between the two

mean of the means. It is then subtracted from 1 to give

the probability P as in (12). In addition the probability

P of the log-normal is multiplied by the ratio of the

number of the vectors as shown in (13),

= P



min

max



(13)

with min

being the landmark i with the minimum

number of vectors and max

the maximum number of

vectors of landmark j. Thus, even if the Euclidean dis-

tance between the two optical ﬂow patterns is small,

the total probability, P

, can be low if the ratio of the

vectors is small. Thus, two patterns which are totally

different may have a small Euclidean distance that

yields a high probability P. Multiplying this proba-

bility value by the ratio of the number of vectors can

drop signiﬁcantly the total probability value, P

, as-

suming that the numbers of vectors are not of the same

magnitude. The landmark of Fig. 3 acts as a reference

for the following snapshots in order to demonstrate

the similarity score at different distances and veloci-

ties, and between different landmarks. The optic ﬂow

images are produced by calculating the motion of a

landmark at two time contiguous frames. It should

also be noted that the ﬂow vectors appear upside down

since the images are read from top to bottom.

4 RESULTS

The homing model described in this paper has been

implemented in the C++ programming language and

the (MATLAB, 2007) software was used for the anal-

ysis of the data. The breve simulator was used for the

development of the 3D environment (Klein, 2002).

BIOLOGICALLY INSPIRED ROBOT NAVIGATION BY EXPLOITING OPTICAL FLOW PATTERNS

649

0 100 200 300 400 500 600

100

150

200

250

Red elem: 113, Blue elem: 84, Divergence: 2.53, Probability: 48.52%

(a) Optical ﬂow pattern of the reference landmark taken at a dis-

tance of 11m and a velocity of 3km/h.

0 100 200 300 400 500 600

100

150

200

250

Red elem: 113, Blue elem: 100, Divergence: 1.19, Probability: 82.04%

(b) Optical ﬂow pattern of the reference landmark taken at a dis-

tance of 14m and a velocity of 4km/h.

Figure 4: Optical ﬂow patterns of the reference landmark

taken at different distances and velocities.

The graphs of Fig. 4 demonstrate the effectiveness of

our approach by comparing the optical ﬂow patterns

of the reference image, Fig. 3, taken at a distance

of 11m and a velocity of 4km/h with the optical ﬂow

patterns of the same landmark but taken at varying

distances and velocities.

The circle in the graphs represents the mean po-

sition of all the vectors that comprise a landmark, in

other words the center of gravity. The red optic ﬂow

vectors refer to the reference image while the blue

ones refer to the current snapshot. Vectors whose

length falls below a threshold (in this case 1) are con-

sidered as outliers. Divergence is the Euclidean dis-

tance between the mean position of the vectors of the

current snapshot with the mean position of the vec-

tors of the reference image. The number of elements

in the current snapshot differs from frame to frame as

the angle of perception changes. From these graphs it

is clear that the similarity score is quite high in both

(a) Tower-like landmark.

0 100 200 300 400 500 600

100

150

200

250

Red elem: 113, Blue elem: 99, Divergence: 30.77, Probability: 0.07%

(b) Optic ﬂow patterns between the tower-like landmark and the

reference landmark.

Figure 5: Comparison of optic ﬂow patterns between a

tower-like landmark and the reference landmark. The dis-

tance of 11m remains the same as in the reference landmark

as well as the velocity taken, that is 4km/h.

ﬁgures revealing that the same landmark has been

observed when comparing the optical ﬂow maps be-

tween the foraging and homing process. Based on this

result the robot is able to localize itself using optical

ﬂow maps.

Figure 5 depicts a tower-like landmark and the

reference landmark of Fig. 3. The distance and ve-

locity at which they were captured remains the same

as in the reference image, that is 11m for distance

and 4km/h for velocity. In the graph of Fig. Please

place \label after \caption, the similarity score

is quite low, that is 0.07% while the divergence is

quite high, that is 30.77. This low probability reveals

that the two landmarks are different to each other.

Finally, in Fig. 6 a pyramid-like landmark is

shown against the optical ﬂow pattern of the reference

landmark. In this case, too, the distance and velocity

have been kept the same as in the reference landmark.

The probability in Fig. Please place \label after

\caption is low, too, that is 4.99% while the di-

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

650

(a) Pyramid-like landmark.

0 100 200 300 400 500 600

100

150

200

250

Red elem: 113, Blue elem: 99, Divergence: 10.21, Probability: 4.99%

(b) Optic ﬂow patterns between the pyramid-like landmark and the

reference landmark.

Figure 6: Comparison of optic ﬂow patterns between a

pyramid-like landmark and the reference landmark. The

distance of 11m remains the same as in the reference land-

mark as well as the velocity taken, that is 4km/h.

vergence between the centers of gravity is equal to

10.21. As in the previous example, the low proba-

bilistic score reveals the dissimilarity of the two land-

marks, even though the distance and the velocity that

the images were captured are the same as in the refer-

ence landmark. It is, however, likely that two dissim-

ilar landmarks may produce a high similarity score.

This can be the case when two landmarks have simi-

lar properties such as texture, shape, and size. In such

a scenario the robot will localize itself inaccurately.

5 CONCLUSIONS

In this paper we presented a novel biologically in-

spired method to tackle the robot homing problem.

In this approach, we have considered only the opti-

cal ﬂow patterns of the landmarks. The simulation

results show that optical ﬂow can be used as a means

to perform homing. This method is parsimonious as

no other information is taken into account such as

position and velocity of the robot. In addition, our

method is computationally efﬁcient as images need

not be stored but the properties of the vectors, that is

the mean of the means of the vectors and the number

of vectors in a snapshot.

Finally, comparing the current method with the

method presented by (Diamantas et al., 2010) we can

infer that the method presented in this paper is more

robust and accurate. In the method of (Diamantas

et al., 2010) the log-normal distribution has a µ = 2.24

and σ = 0.86 whereas in the current work mean and

standard deviation are µ = 1.20 and σ = 0.71, respec-

tively. This biological approach may also help explain

the methods employed by insects, and in particular

honeybees, to perform localization and thus homing.

To support this, a recent study by (Avargues-Weber

et al., 2009) reveals that honeybees are capable of dis-

criminating faces. It could well be the case of optical

ﬂow patterns.

ACKNOWLEDGEMENTS

The authors would like to thank Dr Klaus-Peter Za-

uner for his guidance and help in shaping the optic

ﬂow idea.

REFERENCES

Argyros, A. A., Bekris, C., Orphanoudakis, S. C., and

Kavraki, L. E. (2005). Robot homing by exploiting

panoramic vision. Journal of Autonomous Robots,

19(1):7–25.

Avargues-Weber, A., Portelli, G., Benard, J., Dyer, A., and

Giurfa, M. (2009). Conﬁgural processing enables

discrimination and categorization of face-like stim-

uli in honeybees. Journal of Experimental Biology,

213(4):593–601.

Barron, J. L., Fleet, D. J., and Beauchemin, S. S. (1994).

Performance of optical ﬂow techniques. International

Journal of Computer Vision, 12(1):43–77.

Blackburn, M. and Nguyen, H. (1995). Vision based au-

tonomous robot navigation: Motion segmentation.

In Proceedings for the Dedicated Conference on

Robotics, Motion, and Machine Vision in the Automo-

tive Industries, pages 353–360, Stuttgart, Germany.

Camus, T., Coombs, D., Herman, M., and Hong, T.-S.

(1996). Real-time single-workstation obstacle avoid-

ance using only wide-ﬁeld ﬂow divergence. In Pro-

ceedings of the 13th International Conference on Pat-

tern Recognition, volume 3.

Cartwright, B. and Collett, T. S. (1987). Landmark maps for

honeybees. Biological Cybernetics, 57(1–2):85–93.

BIOLOGICALLY INSPIRED ROBOT NAVIGATION BY EXPLOITING OPTICAL FLOW PATTERNS

651

Cartwright, B. A. and Collett, T. S. (1983). Landmark learn-

ing in bees. Journal of Comparative Physiology A,

151(4):521–543.

Collett, T. (2002). Insect vision: Controlling actions

through optic ﬂow. Current Biology, 12(18):615–617.

Diamantas, S. C. (2010). Biological and Metric Maps

Applied to Robot Homing. PhD thesis, School

of Electronics and Computer Science, University of

Southampton.

Diamantas, S. C., Oikonomidis, A., and Crowder, R. M.

(2010). Towards optical ﬂow-based robotic homing.

In Proceedings of the International Joint Conference

on Neural Networks (IEEE World Congress on Com-

putational Intelligence), pages 1–9, Barcelona, Spain.

Esch, H., Zhang, S., Srinivasan, M., and Tautz, J. (2001).

Honeybee dances communicate distances measured

by optic ﬂow. Nature, 411(6837):581–583.

Frenz, H. and Lappe, M. (2005). Absolute travel distance

from optic ﬂow. Vision Research, 45(13):1679–1692.

Gibson, J. J. (1974). The Perception of the Visual World.

Greenwood Publishing Group, Santa Barbara, CA,

USA.

Hafner, V. V. (2004). Adaptive navigation strategies in

biorobotics: Visual homing and cognitive mapping

in animals and machines. Shaker Verlag GmbH,

Aachen.

Hrabar, S., Sukhatme, G., Corke, P., Usher, K., and Roberts,

J. (2005). Combined optic-ﬂow and stereo-based nav-

igation of urban canyons for a UAV. In Proceedings

of IEEE/RSJ International Conference on Intelligent

Robots and Systems, pages 302–309.

Kendoul, F., Fantoni, I., and Nonami, K. (2009). Optic ﬂow-

based vision system for autonomous 3D localization

and control of small aerial vehicles. Robotics and Au-

tonomous Systems, 57(6–7):591–602.

Klein, J. (2002). Breve: A 3D simulation environment for

the simulation of decentralized systems and artiﬁcial

life. In Proceedings of Artiﬁcial Life VIII, the 8th In-

ternational Conference on the Simulation and Synthe-

sis of Living Systems.

Kral, K. and Poteser, M. (1997). Motion parallax as a source

of distance information in locusts and mantids. Jour-

nal of Insect Behavior, 10(1):145–163.

Lambrinos, D., Moller, R., Labhart, T., Pfeifer, R., and

Wehner, R. (2000). A mobile robot employing insect

strategies for navigation. Robotics and Autonomous

Systems, special issue: Biomimetic Robots, 30(1–

2):39–64.

Langer, M. and Mann, R. (2003). Optical snow. Interna-

tional Journal of Computer Vision, 55(1):55–71.

Lucas, B. D. and Kanade, T. (1981). An iterative image

registration technique with an application to stereo vi-

sion. In Proceedings of the 7th International Joint

Conference on Artiﬁcial Intelligence (IJCAI), August

24-28, pages 674–679.

Madjidi, H. and Negahdaripour, S. (2006). On robustness

and localization accuracy of optical ﬂow computation

for underwater color images. Computer Vision and

Image Understanding, 104(1):61–76.

MATLAB (2007). http://www.mathworks.com/.

Matsuno, F. and Tadokoro, S. (2004). Rescue robots and

systems in Japan. In IEEE International Conference

on Robotics and Biomimetics, pages 12–20.

Merrell, P. C., Lee, D.-J., and Beard, R. (2004). Obsta-

cle avoidance for unmanned air vehicles using opti-

cal ﬂow probability distributions. Sensing and Per-

ception, 5609:13–22.

Ohnishi, N. and Imiya, A. (2007). Corridor navigation and

obstacle avoidance using visual potential for mobile

robot. In Proceedings of the Fourth Canadian Confer-

ence on Computer and Robot Vision, pages 131–138.

OpenCV (2008). http://opencv.willowgarage.com/wiki/.

Schuster, S., Strauss, R., and Gotz, K. G. (2002). Virtual-

reality techniques resolve the visual cues used by fruit

ﬂies to evaluate object distances. Current Biology,

12(18):1591–1594.

Simpson, W. (1993). Optic ﬂow and depth perception. Spa-

tial Vision, 7(1):35–75.

Tautz, J., Zhang, S., Spaethe, J., Brockmann, A., Si, A.,

and Srinivasan, M. (2004). Honeybee odometry: Per-

formance in varying natural terrain. Plos Biology,

2(7):915–923.

Vardy, A. (2005). Biologically Plausible Methods for Robot

Visual Homing. PhD thesis, School of Computer Sci-

ence, Carleton University.

von Frisch, K. (1993). The Dance Language and Orienta-

tion of Bees. Harvard University Press, Cambridge,

MA, USA.

Warren, W. and Fajen, B. R. (2004). From optic ﬂow to

laws of control. In Vaina, L. M., Beardsley, S. A., and

Rushton, S. K., editors, Optic Flow and Beyond, pages

307–337. Kluwer Academic Publishers.

Zufferey, J.-C., Beyeler, A., and Floreano, D. (2008). Optic

ﬂow to control small UAVs. In IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems:

Workshop on Visual Guidance Systems for small au-

tonomous aerial vehicles, Nice, France.

VISAPP 2011 - International Conference on Computer Vision Theory and Applications

652