PREVENTION OF INFORMATION HARVESTING

IN A CLOUD SERVICES ENVIRONMENT

L. M. Batten, J. Abawajy and R. Doss

Deakin University, 221 Burwood Highway, Burwood, Victoria, 3125, Australia

Keywords: Information harvesting, Access, Secret sharing scheme, Cloud computing.

Abstract: We consider a cloud data storage involving three entities, the cloud customer, the cloud business centre

which provides services, and the cloud data storage centre. Data stored in the data storage centre comes

from a variety of customers and some of these customers may compete with each other in the market place

or may own data which comprises confidential information about their own clients. Cloud staff have access

to data in the data storage centre which could be used to steal identities or to compromise cloud customers.

In this paper, we provide an efficient method of data storage which prevents staff from accessing data which

can be abused as described above. We also suggest a method of securing access to data which requires more

than one staff member to access it at any given time. This ensures that, in case of a dispute, a staff member

always has a witness to the fact that she accessed data.

1 INTRODUCTION

The importance of minimizing information leakage

in a cloud computing environment is highlighted by

the current use of the cloud infrastructure for

applications that require strong confidentiality

guarantees. Such applications include e-commerce

services, medical records services and back-office

business (Ristenpart et al. 2009).

Clouds are sources of large datasets that can be

harvested by attackers to obtain private and personal

information that can lead to identity compromise and

can result in both “true” identity theft, where true

information is used to steal the identity of a real

person, and “synthetic” identity theft, where true and

fake information is used to create a fake identity.

Unrestricted and unmonitored access by insiders to

diverse datasets can result in both kinds of identity

theft – hence there is a need to restrict access by

insiders to data stored in cloud data centres.

We note that encryption of data within the cloud

will prevent some unauthorized access; but data

must be decrypted in order to be processed. There is

no current practical method for encryption of data in

such a way that the data can be processed in the

cloud without decryption. However, there is recent

theoretical work in this direction by Gentry (Gentry,

2009), based on homomorphic encryption methods,

suggesting that it may be possible. The problem for

the foreseeable future is that, using this method, the

processing time for even small amounts of data is

infeasible (Cattedu, 2009).

1.1 The Threat Model

We consider a cloud data storage involving three

entities, the cloud service customer (CSC), the cloud

service provider (CSP) which provides services, and

the cloud service operator (CSO) (see Figure 1).

From time to time, as part of their normal work

allocation, staff in the CSP access data in storage.

The data stored in the data storage centre comes

from a variety of customers and some of these

customers may compete with each other in the

market place or may own data which comprises

confidential information about their own clients.

A large number of staff work in the CSP and job

volatility may be high. It is therefore not feasible to

perform elaborate security checks on staff, nor to

monitor them extensively. The staff potentially have

access to data in the data storage centre which could

be used to steal identities to sell on the black market,

or to blackmail a cloud customer.

The objective of this paper is to establish a cloud

architecture which minimizes the opportunity for

such information harvesting.

Batten L., Abawajy J. and Doss R..

PREVENTION OF INFORMATION HARVESTING IN A CLOUD SERVICES ENVIRONMENT .

DOI: 10.5220/0003389700660072

In Proceedings of the 1st International Conference on Cloud Computing and Services Science (CLOSER-2011), pages 66-72

ISBN: 978-989-8425-52-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

1.2 Related Work

In (Wang et al., 2010) a third party auditor is

proposed which employs a series of cryptographic

methods to verify that data has been processed

according to the agreement between the cloud

service and the customer. This is a cumbersome

method that does not scale to large clouds. Although

it prevents reading of data by the auditors, it does

not prevent reading of data by cloud staff.

A completely different approach was taken by

(Parakh and Kak, 2009), who focus on methods of

storing data within the cloud environment by

splitting it into retrievable components before

storing it. Thus, a set of medical records might be

fragmented in such a way that the viewing of one

fragment reveals no usable information to the reader.

The roots of a polynomial are used to allocate data

components to storage locations. The authors admit

that for the management of many large data sets, this

method is inefficient for the purposes of data

processing. They provide an alternate data security

method in this case, whereby a staff member uses a

secret sharing scheme to generate different keys for

different components of a data set and encrypts each

component with a separate key. This protects the

data while in storage from being corrupted. It also

prevents access to the data by any other staff

member. However, it suffers from the drawback that

the staff member generating the keys can access the

entire data set, and must be trusted not to reveal the

keys to others.

In this paper, we provide an efficient method of

data storage which prevents staff accessing data and

which can be used in the threat model described

above. We also suggest a method of securing access

to data which requires more than one staff member

to access it at any given time. This ensures that, in

case of a dispute, a staff member always has a

witness to the fact that she accessed data.

In the next section, we motivate the work with a

detailed scenario based on medical data. In Section

3, we describe the basic cloud storage model and our

approach in separating data within the storage centre

area. Section 4 describes a secret sharing scheme

method for ensuring that no single person may

access a data storage area alone. In Section 5, we

consider how to adapt this scheme to the situation of

staff joining or departing the cloud business centre.

Finally, in Section 6, we draw conclusions and

propose some areas for future work.

2 MOTIVATING SCENARIO

Assume that Jo is an individual whose data is stored

in the databases of a number of organizations; this

includes an automobile registration organization, a

government health plan, a pharmacy and an

insurance company. All four organizations employ

Cloud X to store and process their data. Thus, in

Cloud X, the complete identity information relating

to Jo can be represented as a 4-tuple <C1, C2, C3,

C4>, where Ci, 1 ≤ i ≤ 4, refers to the data of each of

the organizations. If data relating to the different

categories of Jo’s personal identity information is

stored in the same location in a cloud data area, then

it is clear that an insider can easily capture the

identity information required to impersonate her.

Further, having captured the identity information,

the attacker will be able to harvest different types of

information relating to the stolen identity leading to

privacy disclosure. For instance, if C2 was the

individual’s, Medicare number, the insider can

execute a combined query using C3 and C4 on the

medical records database stored in the cloud

infrastructure to synthesize the medical history of a

given individual. This can be attractive especially

for say, medical insurance providers who can then

unfairly take into account the person’s detailed

medical history while assessing their application for

medical insurance cover. By periodic information

harvesting over the datasets in the cloud, expensive

claims can be predicted leading to unfair termination

of insurance policies.

Equally important is the fact that information

such as medical history, medical conditions and

related drug usage is evolving information that can

be exploited by insider abuse (Cavoukian, 2008).

For instance, trends in the medical conditions of “at

risk”, individuals such as the elderly or people with

pre-conditions can be monitored – frequent visits to

the GP may be used as an indicator of a recurring or

on-going medical condition that might result in

hospitalization and possibly an expensive claim or

the prescription of pregnancy-related drugs may be

perceived as indicating the medium to short-term

plans of an individual to start a family.

Hence, while it is important that data be stored in

the cloud in a distributed manner to ensure that

insider compromise is minimized, it is equally

critical that data access is tightly controlled to ensure

that information leakage leading to identity theft and

privacy disclosure can be prevented.

PREVENTION OF INFORMATION HARVESTING IN A CLOUD SERVICES ENVIRONMENT

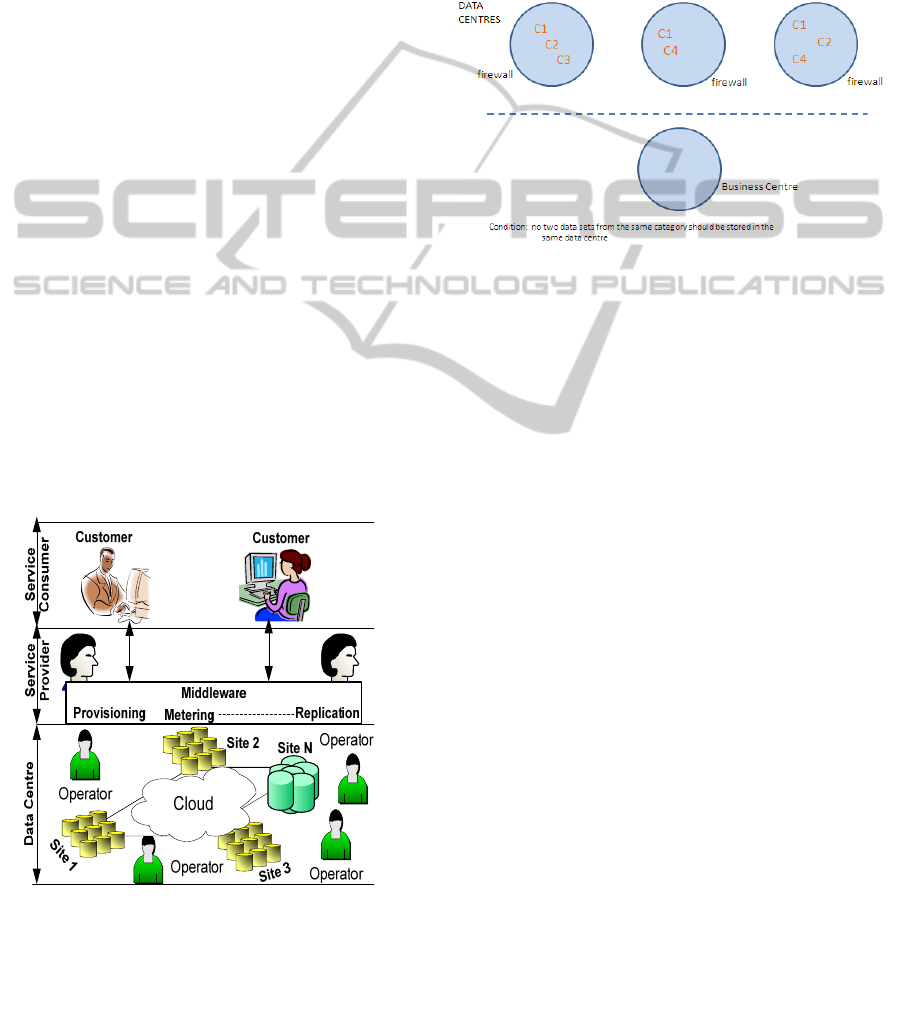
3 THE CLOUD STORAGE

REFERENCE MODEL

We refer again to Figure 1. A CSC rents storage

from a CSP and pays for the amount of storage their

data is actually consuming or for what the CSCs

have allocated. CSCs range from individuals, small

businesses and financial institutions to Fortune 500

firms to governments. The management of the

storage is done solely by the CSOs, and thus CSCs

are relieved of the burden of maintaining storage

infrastructure. The CSOs migrate data between

storage tiers, set up connections, maintain disk

drives, manage firmware upgrades, establish virtual

machine replication timetables, take snapshots as

well as scheduled data backups and are responsible

for safe storage of the backup media (Abawajy,

2009).

The CSPs own the cloud resources and expertise in

building and managing cloud storage servers. They

provide data storage as a service, which is

virtualised storage on demand over a network to

CSCs based on a request for a given, agreed quality

of service. The use of virtualisation allows CSPs to

maximise storage resource utilisation by

multiplexing data storage of many cloud customers

across a shared physical infrastructure. The term

multi-tenancy is commonly used to describe

sharing

of cloud storage among multiple customers who

could be separate companies, or departments within

a company, or even just different applications.

Figure 1: The Cloud Storage Reference Model.

The deployment of data storage as a service is

sites (site 1, site 2, … , site n in Figure 1) over the

Internet running in a simultaneous, cooperative and

distributed manner. Most service providers allow

CSCs to store unstructured database blocks, which

are then mirrored in partial segments over multiple

storage sites. Once the data is stored on the cloud,

CSCs do not control and may not even know the

exact location of their data and copies may be hosted

in the cloud. Thus, a cloud environment can result in

a loss of transparency about where client data is

stored and this can have legal implications.

Figure 2: Secure data storage.

A service consumer is able to perform a variety

of actions on her data including the ability to create,

update, append, reorder and delete their stored data.

The CSCs interact with the cloud servers via the

cloud middleware. The middleware incorporates

components such as different storage protocols

including file-based options and block-based

options, advanced data replication techniques, access

control mechanisms, storage provisioning and

storage metering (Buyya et. al., 2010; Yildiz, et. al.,

2009). CSCs need to allocate storage before they can

use it. Also, the storage usage metering component

provides CSCs with information on how much

storage their data consumed so that they know what

their bill will be at the end of the billing cycle.

The cloud creates unique requirements for data

in terms of security and manageability. Once the

data is stored, it is completely under the control of

the cloud service provider. As users no longer

possess their data locally, it is of critical importance

to assure users that their data are being correctly

stored and maintained (Wang et al., 2010). An

obvious threat to the customer data sets is from

malicious insider abuse. Thus, one of the key issues

in data storage for clouds is to effectively detect any

unauthorized data modification and corruption,

possibly due to server compromise or attacks that

rely upon subverting a cloud’s administrative

functions via malicious insider abuse.

Our aim is to ensure that no employee working

in the cloud can access separate data sets which,

combined, might yield information which is

CLOSER 2011 - International Conference on Cloud Computing and Services Science

considered to be private or confidential. In order to

ensure this, we propose pre-classification of data by

the customer itself according to a cloud service

determination in order to be able to store data in

separate fire-walled and access protected data centre

areas. The customer will be asked to classify its data

into one of several categories. A single category

might be health data such as medical insurance,

hospital and pharmaceutical information. Those data

sets belonging to the same category would be

separated in storage. Figure 2 describes how this

would be done. In the health data example, all three

data sets would be classified as being in the same

category C1 and therefore stored in three separate

areas. Other data not in the same category can be

stored with C1 data as shown in the Figure. The

condition is that no two data sets in the same

category should be stored in the same data centre.

This requires enough data storage centres to store all

data in any one category at any given time. In a

virtual machine environment, however, it is a trivial,

and normal, task to establish additional data centres

as needed.

Figure 3: A secret sharing scheme used in securing access

to data.

4 ACCOUNTABILITY – THE USE

OF SECRET SHARING

SCHEMES

Secret sharing schemes have been used by

(

Upmanyu, 2010) in designing a provably-secure

privacy-preserving protocol to limit access to related

data sets stored in the cloud. Their method is

substantially more efficient than previous known

methods, but still adds noticeable cost to the cloud

service. We approach the goal of securing access in

two ways. One is by means of the cloud architecture

itself, compartmentalizing and separating the storage

spaces, as described in the previous section; the

other is by means of cryptographic access and

authentication procedures. These access and

authentication procedures need to be mapped across

the compartmentalized cloud structure.

Since our aim is to ensure that no employee

working in the cloud can access separate data sets

which, combined, might yield information which is

considered to be private or confidential, a secret

sharing scheme will be used to ensure that no set of

less than t, for some fixed value t, people can

collaborate to gain access to enough data sets from

the same category to be able to deduce information

which is confidential.

DEFINITION: Let t and w be positive integers, t ≤

w. A (t,w)-threshold secret sharing scheme is a

method of sharing a message M among a set of w

participants in such a way that any t participants can

reconstruct the message M, but no subset of smaller

size can reconstruct M.

Adi Shamir invented the first such scheme in

1997 (Menezes et al.,1997) and it is based on the

idea of Lagrange interpolation, or, equivalently, the

fact that knowing n+1 points of a degree n

polynomial determines the whole polynomial.

Here, we shall set up a secret sharing scheme in a

finite field over a prime, GF(p), where a secret M is

represented as a number modulo the prime p, and we

want to split M among w people in such a way that

any t can reconstruct the message, but no fewer than

t people can do so.

We randomly choose t-1 coefficients s

(mod p)

and define the polynomial

s(x) = M+s

x+…+s

t-1

t- 1

(mod p) (1)

Any of p possible choices for x will result in a value

for s(x). These values need not all be distinct. We

can thus distribute up to p ‘shares’ in the secret to

participants, of the form (x, s(x)). Note that s(0) = M,

so this share will not be used. As long as w ≤ p-1, we

have a (t,w)-threshold secret sharing scheme as any t

participants can combine their shares and solve a

system of equations which will determine M. No

fewer than t people can do this.

In a cloud services situation, some staff may

have seniority which permits them to hold more than

one share of a secret which allows access to a data

centre; this will be determined in-house. However,

no matter how many shares of a secret a person

holds, they should never have enough shares to

determine the secret alone. This ensures that each

employee can be held accountable for accessing a

data centre based on the evidence of a third party; it

also provides a witness to the fact that an employee

acted appropriately in accessing data.

PREVENTION OF INFORMATION HARVESTING IN A CLOUD SERVICES ENVIRONMENT

In addition, the same set of people should never

be able to access two data centres holding

information which cannot be shared. Thus,

conditions on distribution of any secret sharing

scheme apply as below.

CONDITIONS:

(i) Any data centre needs at least two people to be

able to access it,

(ii) The same set of people should never hold shares

to a key accessing different data centres holding data

of the same category.

Figure 3 describes the data and business centres with

access based on secret sharing schemes.

Example: Here, we give an example of a secret

sharing scheme which satisfies the two conditions

above. Let M = 190503180520 be the secret message

and let p = 1234567890133. (Note that p is greater

than M.). We construct a (3,6)-threshold scheme as

follows. We choose

s(x) = M + 482943028839x + 1206749628665x

modulo p

where s

= 482943028839 and s

= 1206749628665.

And now we distribute shares of the secret to 8

participants, using values of x from 1 to 8. The

shares are:

 (1, 645627947891)

 (2, 1045116192326)

 (3, 154400023692)

 (4, 442615222255)

 (5, 675193897882)

 (6, 852136050573)

 (7, 973441680328)

 (8, 1039110787147)

The first four people are each given one share,

person i receiving share (i, s(i)) above.

Person 5 is given shares 5 and 6 and person 6 is

given shares 7 and 8. Since 3 shares are needed to

determine the secret, condition (i) automatically

applies.

Suppose shares 1, 2 and 7 are allocated to access

the first data centre in Figure 3. Then shares 1, 2 and

8 cannot be allocated to access the second or the

third data centres; this is because the same person

holds shares 7 and 8 and can use either, together

with share-holders 1 and 2 to breach condition (ii).

A cloud service business is dynamic; staff come

and go, as do data and files. If an additional data

centre must be set up, then the existing secret

sharing scheme must be adapted to cope without a

complete re-distribution of secret shares. Similarly,

if a staff member arrives or departs, shares need to

be allocated or deleted from the existing scheme. In

this paper, we discuss only this latter case of a

dynamic staffing situation. We leave a dynamic data

situation for future work as it requires a different

approach.

5 A DYNAMIC STAFFING

SITUATION AND DYNAMIC

SECRET SHARING SCHEMES

Each data centre is accessed by means of a secret M

from a secret sharing scheme as in equation (1). In

order that condition (ii) be maintained, it is

necessary to use different equations for different

data centres. Nevertheless, different equations with

the same secret for different data centres is

permissible as different sets of shares need to be

used to compute the secret.

5.1 Extending Secret Sharing Schemes

in Order to Add Staff

The lemmas in this section describe how to adjust

secret sharing schemes to accommodate staff who

leave or join the service provider. Lemma 1 shows

that as long as the parameters are within prescribed

bounds, an additional staff member can easily be

accommodated.

LEMMA 1: Let t and w be positive integers, 2 ≤ t ≤

w ≤ p-1, p a prime. Any (t,w)-threshold secret

sharing scheme over GF(p) based on (1) with w +1

≤ p - 1 can be extended to a (t,w+1)-threshold

secret sharing scheme over GF(p) also based on (1).

PROOF. Suppose we have a (t,w)-threshold secret

sharing scheme over GF(p) based on (1) with w +1 ≤

p - 1. Since w < p – 1, we can distribute an

additional share based on (1), thus resulting in a

(t,w+1)-threshold secret sharing scheme over GF(p).

QED.

The above lemma and its proof describe how a staff

member can be added to a scheme which continues

to need t members to access a secret. As long as the

bounds are met, members can continue to be added.

We thus have the following.

COROLLARY: Let t, w and r be positive integers,

2 ≤ t ≤ w ≤ w+r ≤ p-1, p a prime. Any (t,w)-

threshold secret sharing scheme over GF(p) based

on (1) with w +1 ≤ p - 1 can be extended to a

(t,w+r)-threshold secret sharing scheme over GF(p)

also based on (1).

In order to allow flexibility in adding many staff, the

prime p is normally chosen to be much larger than

CLOSER 2011 - International Conference on Cloud Computing and Services Science

the potential number of staff. The situation of staff

departing is somewhat more difficult. The shares of

departing staff must be revoked and we deal with

this in the next two sub-sections.

5.2 Revocation Lists

As staff leave, each data centre stores revoked

shares. To prevent a set of t shares, at least one of

which is revoked, from accessing a secret M

associated with a data centre, the polynomial (1) is

adjusted to the following:

s(x) = (M*Π(x – r

))/Π(x – r

) + s

x + … + s

t-1

(mod p) (2)

where the product is taken over the abscissa of each

revoked share. When a non-revoked value for x is

substituted, the coefficient of M is 1, and (2) reduces

to (1). However, when a revoked value for x is used,

the coefficient of M is not computable, M is not

revealed and access is denied.

Revocation can continue to the point where

precisely t associated shares are available to access a

data centre, but not beyond. The service provider

must ensure that enough shares are available at any

time in order to access the data centre. Thus, we

have the following lemma.

LEMMA 2: Any (t,w)-threshold secret sharing

scheme over GF(p) based on (2) with 2 ≤ t ≤ w ≤ p-

1, p a prime, permits revocation of up to w-t shares

while still operating as a (t,r)-threshold secret

sharing scheme over GF(p) based on (2) with 2 ≤ t

≤ r ≤ w ≤ p-1.

If a revoked share is used in attempting to gain

access to a data centre, the authentication centre can

determine which share it was and hence also to

whom it belongs. While equation (2) does not reveal

this, the following does. Once a set of t shares fails

to produce the secret, the authentication centre

compares each submitted share with each entry in

the list of revoked shares to find a match and thus

also identifies the owner.

5.3 Managing Revocation Lists

Since p-1 shares can be distributed, up to p-1-t

shares can be revoked with a usable secret sharing

scheme remaining. Once p-1-t+1 = p-t shares are

revoked, the scheme is no longer usable and a new

threshold secret sharing scheme must be deployed.

The current share holders may retain their

existing shares if a new polynomial is designed in

the following way: retain the t-1 or fewer existing

valid shares. Choose additional pairs randomly, but

excluding all revoked shares from the first scheme,

so that a total of t’ pairs is available where t’ is to be

the threshold of the new scheme. Use these t’ pairs

to determine uniquely a polynomial of the form (1)

over some (large) prime p’. This new polynomial

can now be used to formulate p’ shares, such that the

holders of old shares retain these.

6 CONCLUSIONS

AND FUTURE WORK

We have presented two approaches, which can be

combined, to protection of data inside a cloud

service centre. One, expressed in Figure 2, stores the

data in such a way as to separate data of similar

‘types’. The second deals with allocating shares to

cloud staff in such a way that access to more than

one data set of the same type is prevented. Thus, in

allocating shares, conditions (i) and (ii) must not be

violated; refer to Figure 2.

We showed that in such a setting revocation of

up to a certain number of shares distributed to staff

can be easily managed.

We leave for future work the following problem:

automate an efficient scheme for allocation of shares

in a dynamic environment (staff leaving and joining)

such that conditions (i) and (ii) are always valid.

Extend this scheme so that it includes the addition

and removal of data centres.

REFERENCES

Abawajy, J. 2009. Determining Service Trustworthiness.

In Intercloud Computing Environments, Proc. of the

10th IEEE International Symposium on the Pervasive

Systems, Algorithms and Networks (ISPAN 2009), pp:

784-788, 2009.

Buyya, R., Beloglazov, A. and Abawajy, J. 2010. Energy-

Efficient Management of Data Center Resources for

Cloud Computing: A Vision, Architectural Elements,

and Open Challenges. In Proc. of PDPTA 2010, pp: 6-

20, July 12 - 15, Las Vegas, Nevada.

Cattedu, D. and Hogben, G., editors. ‘Cloud

computingsecurity benefits, risks and

recommendations’, Nov. 2009 – Report by the

European Network andInformation Security Agency.

Cavoukian, A., 2008. Privacy in the Clouds. In Indentity

inthe Information Society (pp. 89-108). Springer.

Gentry, C. (2009) ‘Fully homomorphic encryption

usingideal lattices’. Proceedings of the 41st

annualACM symposium on Theory of computing,

ACM, New York, pp. 169-178.

Menezes, A., van Oorschot, P. and Vanstone, S. 1997.

Handbook of Applied Cryptography. CRC PressBoca

PREVENTION OF INFORMATION HARVESTING IN A CLOUD SERVICES ENVIRONMENT

Raton, USA.

Parakh, A. and Kak, S. 2009. Online data storage using

implicit security. Information Sciences 179

(2009)3323-3331.

Ristenpart, T., Tromer, E., Shacham, H., & Savage, S.

(2009). Hey, You, Get off of my Cloud: Exploring In-

formation Leakage in Third Party Compute Clouds.

CCS'09, (pp. 199 - 210). Chicago, Illinois, USA.

Upmanyu, M., Namboodiri, A., Srinathan, K. and

Jawahar, C. V. 2010. ‘Efficient Privacy Preserving K-

Means Clustering’ PAISI 2010, LNCS 6122, pp. 154–

166.

Wang, C., Wang, Q., Ren K. and Lou, W. 2010 “Privacy-

Preserving Public Auditing for Storage Security in

Cloud Computing,” Proc. IEEE INFOCOM ‘10, Mar.

2010.

Yildiz, M., Abawajy, J., Ercan, T. and Bernoth, A., 2009.

A Layered Security Approach for Cloud Computing

Infrastructure. In Proc. of the 10th IEEE International

Symposium on Pervasive Systems, Algorithms and

Networks (ISPAN 2009), pp. 763-767, 2009.

CLOSER 2011 - International Conference on Cloud Computing and Services Science