
NON-LINEAR LOW-LEVEL IMAGE PROCESSING IMPROVEMENT
BY A PURPOSELY INJECTION OF NOISE
A. Histace
ETIS UMR CNRS 8051, ENSEA-UCP, 6 avenue du Ponceau, 95014 Cergy, France
Keywords:
Stochastic resonance, Low-level image processing, Binarization.
Abstract:
It is progressively realized that noise can play a constructive role in nonlinear formation processes. The
starting point of the investigation of such useful noise effect has been the study of the Stochastic Resonance
(SR) effect. The goal of this article is to propose a direct application of SR phenomenon in image processing,
for the interest of SR in that domain is growing-up. As a prolongation of previous work already presented in
the literature by author, we propose to quantitatively show that a purposely injection of a gaussian noise in a
classical nonlinear image process, as image binarization, can play a constructive action. This work can also
be interpreted as a first step for a better understanding of SR in image processing relating it to classical results
obtained in a nonlinear signal processing framework for classical low-level image processing tool.
1 INTRODUCTION
It is progressively realized that noise can play a con-
structive role in nonlinear formation processes. The
starting point of the investigation of such useful noise
effect has been the study of the Stochastic Resonance
(SR) effect. This paradoxical effect was first intro-
duced some twenty years ago in the domain of cli-
mate dynamics, as an explanation for the regular re-
currences of ice ages (Benzi et al., 1982). Following
this, SR effect has been introduced in nonlinear signal
processing to describe the mechanism of a construc-
tive action of a white Gaussian noise in the transmis-
sion of a sinusoid by a nonlinear dynamic system gov-
erned by a double-well potential. From this time, the
phenomenon of stochastic resonance has experienced
large varieties of extensions with variations concern-
ing the type of noise, the type of information carry-
ing signal or the type of nonlinear system interacting
with the signal-noise mixture (see for example (Gam-
maitoni et al., 1998) for a review in physics, (Harmer
et al., 2002) for an overview in electrical engineering
and (Chapeau-Blondeau and Rousseau, 2002) for the
domain of signal processing). All these extensions of
the original setup preserve the possibility of improv-
ing the processing of a signal by means of an increase
in the level of the noise coupled to this signal. At the
moment, new forms of useful noise effect, related to
stochastic resonance, continue to be demonstrated. A
recent specific domain of interest for the study of this
useful noise effect is nonlinear image processing (see
(Morfu et al., 2008) for instance).
The goal of this article is to propose a direct appli-
cation of SR phenomenonin image processing, for the
interest of SR in that domain is growing-up. As au-
thors have already shown it in (Histace and Rousseau,
2006; Histace and Rousseau, 2010), a possible appli-
cation field is nonlinear image restoration. Neverthe-
less, in order to have a better understanding of the
process and the constructive action of noise, we pro-
pose to study a more simple image processing tool:
Image binarisation.
The main layout of this article is the following:
Second section proposes a presentation of the global
framework of stochastic resonance non limited to im-
age processing. Whereas such presentation has al-
ready been made in various articles, it bears important
historical and conceptual significance. For this rea-
son, we choose to remain it. Third section deals with
application of SR phenomenon to image binarization.
Finally, results will be concluded and discussed.
2 A COMMON FRAMEWORK
FOR STUDY OF SR EFFECT IN
NONLINEAR PROCESSING
Today, it is now widely assumed that a global frame-
work for SR can be defined for all type of demon-
strated effects (Chapeau-Blondeau, 2000).
Stochastic resonance involves four essential ele-
226
Histace A..
NON-LINEAR LOW-LEVEL IMAGE PROCESSING IMPROVEMENT BY A PURPOSELY INJECTION OF NOISE.
DOI: 10.5220/0003399202260229
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2011), pages 226-229
ISBN: 978-989-8425-47-8
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ments: (i) an information-carrying or coherent signal
s: it can be deterministic, periodic or non, or random;
(ii) a noise η, whose statistical properties can be of
various kinds (white or colored, Gaussian or non,... );
(iii) a transmission system, which generally is nonlin-
ear, receiving s and η as inputs under the influence
of which it produces the ouput signal y; (iv) a per-
formance or efficacy measure, which quantifies some
“similarity” between the output y and the coherent in-
put s (it may be a signal-to-noise ratio, a correlation
coefficient, a Shannon mutual information, ...). SR
takes place each time it is possible to increase the
performance measure by means of an increase in the
level of the noise η. Historically, the developments
of SR have proceeded through variations and exten-
sions over these four basic elements. From the origin
and as it has already been mentioned in previous sec-
tion, SR studies have concentrated on a periodic co-
herent signal s, transmitted by nonlinear systems of a
dynamic and bistable type (McNamara and Wiesen-
feld, 1989). This form of SR now appears simply as a
special form of SR. This primary form of SR will not
be entirely described in this article but a complete de-
scription can be found in (Chapeau-Blondeau, 2000)
for instance. For illustration, we propose to illustrate
phenomenon of SR in the framework of image trans-
mission as it was formerly proposed in (Chapeau-
Blondeau, 2000). This example has the advantage of
its simplicity which makes both theoretical and ex-
perimental analysis possible. Leaning again on the
general scheme of SR phenomenon, author considers
this time that the coherent information-carrying sig-
nal s is a bidimensional image where the pixels are
indexed by integer coordinates (i, j) and have inten-
sity s(i, j). For a simple illustration, a binary image
with s(i, j) ∈ {0, 1} is considered for experiment. A
noise η(i, j), statistically independent of s(i, j), lin-
early corrupts each pixel of image s(i, j). The noise
values are independent from pixel to pixel, and are
identically distributed with the cumulative distribu-
tion function F
η
(u) = Pr{η(i, j) ≤ u}. A nonlinear
detector, that it is taken as a simple hard limiter with
threshold θ, receives the sum s(i, j) + η(i, j) and pro-
duces the output image y(i, j) according to:
If s(i, j) + η(i, j) > θ then y(i, j) = 1,
else y(i, j) = 0.
(1)
When the intensity of the input image s(i, j) is low
relative to the threshold θ of the detector, i.e. when
θ > 1, then s(i, j) (in the absence of noise) remains
undetected as the output image y(i, j) remains a dark
image. Addition of the noise η(i, j) will then allow
a cooperation between the intensities of images s(i, j)
and η(i, j) to overcome the detection threshold. The
result of this cooperative effect can be visually appre-
ciated on Fig. 1, where an optimal nonzero noise level
maximizes the visual perception.
Figure 1: The image y(i, j) at the output of the detector of
Eq. (1) with threshold θ = 1.2, when η(i, j) is a zero-mean
Gaussian noise with rms amplitude 0.1 (left), 0.5 (center)
and 2 (right).
To quantitatively characterize the effect visually
perceived in Fig. 1, an appropriate quantitative mea-
sure of the similarity between input image s(i, j) and
output image y(i, j), is provided by the normalized
cross-covariancedefined in (Vaudelle et al., 1998) and
given by:
C
sy
=
h(s− hsi)(y− hyi)i
p
h(s− hsi)
2
ih(y− hyi)
2
i
, (2)
where h.i denotes an average over the images.
C
sy
can be experimentally evaluated through pix-
els counting on images similar to those of Fig. 1.
Also, for the simple transmission system of Eq. (1),
C
sy
can receive explicit theoretical expressions, as a
function of p
1
= Prs(i, j) = 1 the probabilty of a pixel
at 1 in the binary input image s(i, j), and as a function
of the properties of the noise conveyed by F
η
(u) as
mentioned in (Vaudelle et al., 1998).
Considering the above scenario, Fig. 2 showsvari-
ations of C
sy
function of rms amplitude of the input
noise η.
As one can see on Fig. 2, measure of cross-
covariance as defined Eq. (2) identify a maximum
efficacy in image transmission for an optimal nonzero
noise level. This simple example is interpreted here as
the first formalized instance of SR for aperiodic bidi-
mensionnal input signal s (even if it is not clearly an
image processing application).
We are now going to show that this kind of ap-
proach can be successfully transposed in a classical
low-level image processing tool.
3 NOISE-AIDED IMAGE
BINARIZATION
Let’s consider image of Fig. 3. Let’s now consider
that our main goal is to binarize image of Fig. 3 in or-
der to automatically extract barycenter of each coin.
NON-LINEAR LOW-LEVEL IMAGE PROCESSING IMPROVEMENT BY A PURPOSELY INJECTION OF NOISE
227
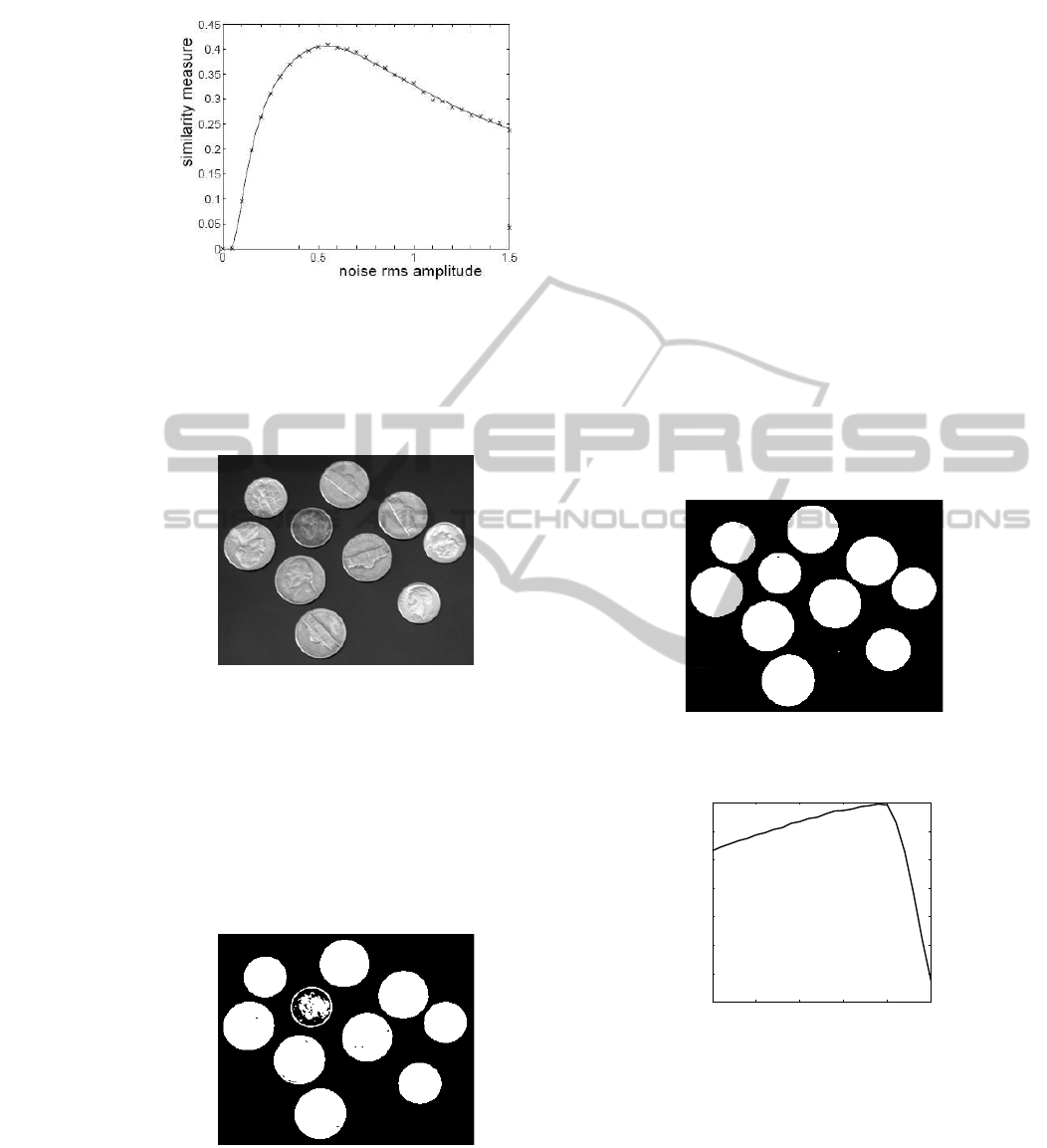
Figure 2: Input-output cross-covariance of Eq. (2) between
input image s(i, j) and output image y(i, j), as a function
of the rms amplitude of the noise η(i, j) chosen zero-mean
Gaussian. The crosses are experimental evaluations through
pixels counting on images, the solid lines are the theoreti-
cal predictions (p
1
= 0.6) calculated by authors (Chapeau-
Blondeau, 2000).
Figure 3: “coins” Image.
Classically, this task can be tackled by an automatic
estimation of the optimal threshold corresponding to
data to binarize. For instance, existing functions usu-
ally use Otsu’s method (Otsu, 1979), which chooses
the threshold to minimize the intraclass variance of
the black and white pixels. Applying that kind of
function to “coins” image leads to binarization results
of Fig.4.
Figure 4: Binarized “coins” image using classical Otsu’s
method for automatic computation of optimal threshold
level.
As one can notice, this approach is not satisfying
since one coin (characterized by an average grey-level
less important than other coins) will not be clearly de-
tected during following processing steps. Empirical
manual setting of the threshold can lead to more in-
teresting results as shown Fig. 5.
Let’s now consider, that existing method of Fig. 4
is a black box with no possibility to manually adjust
threshold value to reach optimal result of Fig. 5.
Considering the classical framework of SR phe-
nomenon, we now purposely corrupt original “coins”
image with a white gaussian noise η of tunable stan-
dard deviation σ
η
. Proposed process is then described
by same equations as Eq. (1) with threshold θ corre-
sponding to the value automatically computed thanks
to Otsu’s approach. In order to quantify the possible
benefit of such addition, we choose to perform a mea-
sure of the normalized cross covariance of Eq. (2)
between optimal result of Fig. 5 and obtained results
for each value of σ
η
. Result of this quantitative study
is presented Fig. 6.
Figure 5: Binarized “coins” image using manual setting for
threshold value.
0 0.05 0.1 0.15 0.2 0.25
0.84
0.86
0.88
0.9
0.92
0.94
0.96
0.98
σ
η
similarity measure
Figure 6: Normalized cross-covariance of Eq. (2) function
of uniform purposely injected noise level σ
η
.
As one can notice on Fig. 6, it is possible to reach
an optimal value of the normalized cross-covariance
for a non zero amount of noise. This is the classi-
cal signature of a SR phenomenon as demonstrated in
previous section for nonlinear binary image transmis-
sion. One can also notice that the normalized cross-
covariance fastly decrease once the optimal value is
VISAPP 2011 - International Conference on Computer Vision Theory and Applications
228

Figure 7: Optimal binarization result obtained for σ
η
=
0.19.
reached: The large amount of corresponding noise,
finally, completely degrade image information. Visu-
ally speaking, the optimal corresponding result pre-
sented Fig. 7 is very close from the optimal one of
Fig. 5. Detection of the whole set of coins is now
possible thanks to the purposely injection of η noise.
Moreover, this experiment shows that it is now pos-
sible to adjust the inner threshold value of the bina-
rization process thanks to an external tuning of noise
level σ
η
.
4 CONCLUSIONS
In this article, we show that the now well known SR
phenomenon can find application in low-level image
processing. More precisely, we show, thanks to a sim-
ple experiment, that a purposely injection of noise in
a classical non tunable binarization process can lead
to interesting results in term of optimal parameters
setting. This is shown here as a proof of feasibility
and more experiment will be made in order to clearly
identify both theoretically and quantitatively the ben-
efit of such an approach for more complex image pro-
cessing tools as nonlinear image restoration for in-
stance. This work can also be interpreted as a first step
for a better understanding of SR in image processing
relating it to classical results obtained in a nonlinear
signal processing framework.
ACKNOWLEDGEMENTS
Author wants to thank Dr. David Rousseau from Uni-
versity of Angers (LISA) for his precious help and
advises about this work.
REFERENCES
Benzi, R., Parisi, G., Sutera, A., and Vulpiani, A. (1982).
Stochastic resonance in climatic changes. Tellus,
34:10–16.
Chapeau-Blondeau, F. (2000). Noise, Oscillators and Al-
gebraic Randomness- From Noise in Communication
Systems to Number Theory, volume 550 of Lecture
Notes in Physics, chapter Stochastic resonance and the
benefit of noise in nonlinear systems, pages 137–155.
Springer (Berlin).
Chapeau-Blondeau, F. and Rousseau, D. (2002). Noise im-
provements in stochastic resonance: From signal am-
plification to optimal detection. Fluctuation and noise
letters, 2:221–233.
Gammaitoni, L., Hangi, P., Jung, P., and Marchesoni, F.
(1998). Stochastic resonance. Reviews of Modern
Physics, 70:223–287.
Harmer, G., Davis, B., and Abott, D. (2002). A review
of stochastic resonance: Circuits and measurement.
IEEE Transactions on Instrumentation and Measure-
ment, 51:299–309.
Histace, A. and Rousseau, D. (2006). Constructive action of
noise for scalar image restoration. Electronics Letters,
42(7):393–395.
Histace, A. and Rousseau, D. (2010). Noise-enhanced Non-
linear PDE for Edge Restoration in Scalar Images.
In IEEE, editor, Proceedings of SOCPAR 2010 SOft
Computing and PAttern Recognition, page accepted,
Cergy France.
McNamara, B. and Wiesenfeld, K. (1989). Theory of
stochastic resonance. Physical Review A, 39:4854–
4869.
Morfu, S., Marqui, P., Nofil, B., and Ginhac, D. (2008).
Nonlinear systems for image processing. Advances in
imaging and electron. physics.
Otsu, N. (1979). A threshold selection method from gray-
level histograms. IEEE Transactions on Systems,
Man, and Cybernetics, 9(1):62–66.
Vaudelle, F., Gazengel, J., Rivoire, G., Godivier, X., and
Chapeau-blondeau, F. (1998). Stochastic resonance
and noise-enhanced transmission of spatial signals in
optics: The case of scattering. Journal of the Optical
Society of America B, 13:2674–2680.
NON-LINEAR LOW-LEVEL IMAGE PROCESSING IMPROVEMENT BY A PURPOSELY INJECTION OF NOISE
229
