DOUBLE PRECISION SPARSE MATRIX VECTOR

MULTIPLICATION ACCELERATOR ON FPGA

Sumedh Attarde, Siddharth Joshi, Yash Deshpande

Electrical Engineering Department, Indian Institute of Technology Bombay, Bombay, India

Sunil Puranik

Computational Research Laboratories, Pune, India

Sachin Patkar

Electrical Engineering Department, Indian Institute of Technology Bombay, Bombay, India

Keywords:

Sparse matrix vector multiplication, FPGA, Embedded scientiﬁc computing, DRAM.

Abstract:

In this paper, we present the design of an embedded system performing double precision sparse matrix vec-

tor multiplication (SpMxV), a key scientiﬁc computation kernel in iterative solvers, for very large matri-

ces (millions of rows). The embedded system is implemented using the Xilinx MicroBlaze platform on the

XUPV5-LX110T FPGA development board. Due to their size, matrices generally encountered in scientiﬁc

computation need to be stored on off-chip DRAMs. A novel processing paradigm involving blocking of the

matrix, and a novel data access mechanism which pre-fetches required data in bursts from off-chip DRAMS

to hide large DRAM random access latencies are proposed and implemented. The processing element has

been implemented as a prototype accelerator peripheral in an embedded system for the iterative Gauss-Jacobi

algorithm.

1 INTRODUCTION

Modern embedded computing devices call for in-

creasingly complex functionality. Commercial hand-

held devices (smartphones) need to perform heavy

image processing, image reconstruction tasks. Engi-

neering applications like seismic imaging, oil explo-

ration require enormous amounts of scientiﬁc com-

puting to be done in a short time on-site. Tradi-

tionally, an enormous amount of computing power

is used for such scientiﬁc computation, which is dif-

ﬁcult to be deplyed in a hand-held device. Such

applications would beneﬁt from compact embedded

solutions which could be deployed in such scenar-

ios. Developing low-power embedded systems capa-

ble of handling large scientiﬁc computations certainly

seems to be a step in this direction when the world is

moving towards energy efﬁcient alternatives.

Sparse Matrix Vector Multiplication (SpMxV) is a

key computational kernel in many scientiﬁc and engi-

neering applications. Least square problems, eigen-

value problems, FEM, computational ﬂuid dynam-

ics, image reconstruction in medical imaging, oil

exploration, seismic imaging, circuit analysis, web-

connectivity and many more applications need to

solve sparse linear systems using iterative methods.

These problems generally involvevery large matrices,

of the order of tens of millions of non-zero elements.

Embedded systems impose constraints pertaining

to area, power and response time. The memory sub-

system is affected by all these components. For the

application at hand, large amounts of memory are the

primary requirement. Thus in order to achieve high

memory density, DRAMs (Dynamic RAMs) offer the

most viable solution. Large matrices which have sizes

running into millions of rows cannot ﬁt in the caches

of general purpose processors. Since memory ac-

cesses are irregular, cache hierarchy loses its effec-

tiveness and many random accesses to high latency

DRAMs are made. This causes performance of Sp-

MxV to drop to a fraction of peak performance for

general purpose processors. It is only by optimiza-

476

Attarde S., Joshi S., Deshpande Y., Puranik S. and Patkar S..

DOUBLE PRECISION SPARSE MATRIX VECTOR MULTIPLICATION ACCELERATOR ON FPGA.

DOI: 10.5220/0003400804760484

In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2011), pages

476-484

ISBN: 978-989-8425-48-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

tion and tuning of SpMxV kernels for the speciﬁc

matrix structures that these shortcomings can be over-

come(Williams et al., 2007).

Modern FPGAs provide abundant resources for

ﬂoating point computations. Aside from large logic

capabilities, these FPGAs also have sufﬁcient on-chip

single-cycle access blocks of RAM (BRAMs) to pro-

vide required on-chip memory bandwidth. On the

other hand, a large number of I/O pins are available

to provide high memory bandwidth in case external

off-chip memories are to be used. However, off-chip

memories like DRAMs have large access latencies

and can considerably slow down the system if used

naively.

We present the design of a prototype embedded

system geared to accelerate SpMxV for scientiﬁc

computing. Since such an embedded system relies on

high random access latency DRAMs, data is stored

in a fashion amenable to burst accesses, thus hiding

DRAM access latencies. The Xilinx MicroBlaze plat-

form was chosen as platform for the embeddedsystem

and implemented on the Xilinx XUPV5-LX110T de-

velopment board.

2 PROBLEM DESCRIPTION

SpMxV requires that two elements - a non-zero ele-

ment from the matrix and an element from the vec-

tor - be fetched and multiplied. The result is accu-

mulated into the appropriate result vector element.

Thus two operations - a multiply and an accumulate

- are performed for every pair of the two elements.

These elements are not required for further process-

ing and are thus discarded. Only the result of the

multiply-accumulate operation is stored. Since two

input words are useful for only two computation oper-

ations, the ratio of computation to bandwidth require-

ment is low compared to other applications (namely

general matrix-matrix multiplication). This ratio be-

comes worse due to overhead of bandwidth require-

ment for fetching pointers - two per matrix element.

Assuming 32-bit pointers and double precision ﬂoat-

ing point matrix and vector data, 24 bytes are fetched

in order to perform 2 ﬂoating point operations. Hence,

the performanceof SpMxV is usually less than a tenth

of the bandwidth available to the system.

Though modern FPGAs have large amounts of

fast access memories, they still fall short of the

amount of storage required in case the matrix and/or

vector data is to be stored in on-chip memories. The

largest Virtex-5 device has less than 24 Mb of storage

and devices in the the latest Virtex-6 family too has

less than 48 Mb of on-chip memory. Assuming 64-bit

data, this translates to 0.4M words and 0.8M words

in case of Virtex-5 and Virtex-6 devices respectively.

Moreover, as discussed in the above paragraph, if vec-

tor elements need to be replicated, then the size of the

matrices that can be handled drops far short of the

one million rank. Hence, an implementation geared

to handle matrices having multi-million rows has to

use external DRAMs for storage.

2.1 Related Work

We shall be referring to the work done by Prasanna

(Zhuo and Prasanna, 2005), Gregg (Gregg et al.,

2007), deLorimier (deLorimier and DeHon, 2005),

Sun (Sun et al., 2007) and Kuzmanov (Kuzmanov and

Taouil, 2009). The ﬁrst three implementations aim

to accelerate iterative solvers via SpMxV on FPGAs.

With the exception of the architecture developed by

Gregg, DRAMs have not been used as the main stor-

age for matrix and vector data.

The SpMxV kernel implemented in a multi-FPGA

architecture by Zhuo and Prasanna was among the

earliest in the ﬁeld. They use Compressed Row Stor-

age (CRS) format for their input which trims the ze-

ros from the sparse matrix rows. In their architecture,

each trimmed row is divided into sub-rows of ﬁxed

length equal to the number of processing elements.

The dot products in a sub-row are assigned to differ-

ent processing elements and then a reduction circuit is

used to get the ﬁnal vector element after all sub-rows

have been processed. This updated value is stored in a

second FPGA, and communication costs are reduced

for conjugate-gradient (CG) routine across iterations.

Optimizations to their design include load balancing

by merging appropriate sub-rows and padding them

with zeros if necessary, which signiﬁcantly improves

performance. However the architecture proposed by

them relies on SRAMs for storage of matrix entries

which severely limits the matrix size. Large num-

ber of parallel accesses to the SRAMs contributes to

a bottleneck in the design. Moreover the entire vec-

tor is replicated in local storage of all processing ele-

ments. The sequential nature of the inputs to the al-

ready huge reduction circuit results in very high la-

tencies. The largest matrix evaluated had 21200 rows

and 1.5 million non-zeros. They reported an average

performance of 350 MFLOPS on a Virtex-II Pro de-

vice.

Special care has been taken by Gregg et. al to cre-

ate a DRAM based solution. They use pre-existing

SPAR architecture originally developed for ASIC im-

plementation and hence port a deeply pipelined de-

sign for FPGA implementation. They use local

BRAMs to create a cache for the DRAM data since

DOUBLE PRECISION SPARSE MATRIX VECTOR MULTIPLICATION ACCELERATOR ON FPGA

477

they consider elimination of cache misses to be of

paramount importance. They reported performance

of 128 MFLOPS for three parallel SPAR computation

units. In case caching is perfect, they achieve perfor-

mance of 570 MFLOPS for three SPAR units.

The architecture developed by deLorimier uses lo-

cal FPGA Block RAMs (BRAMs) exclusively to store

matrix as well as vector data. While pre-processing

the matrix, they exploit the statically available infor-

mation to schedule computation and communication

periods statically. The relevant micro-codeis stored in

the local storage of each processing element. To max-

imize operating frequency, the accumulator used has

a deep pipeline which could potentially cause RAW

(read after write) hazards due to the inherent feedback

in the accumulator data-path. During pre-processing,

they re-order the matrix and interleave rows to pre-

vent RAW hazards thus circumventing the need for

expensive pipeline stalls which might have had to be

enforced. However, the architecture has an enforced

communication stage which is not overlapped with

computation stage, decreasing the overall efﬁciency

of the system. The main limitation of the system is

its inability to handle designs larger than what the

BRAMs can accommodate. The largest matrix evalu-

ated had 90449 rows and 1.8 million non-zeros. They

reported performance of 1.6 GFLOPS for 1 Virtex-II

6000 and about 750 MFLOPS per FPGA with 16 FP-

GAs.

The architecture implemented by Kuzmanov

(Kuzmanov and Taouil, 2009), is capable of being dy-

namically conﬁgured to perform sparse matrix-vector

multiplication or dense matrix-vector multiplication

based on the sparsity of the matrix. The design is im-

plemented on an Altix 450 machine with SGI RASC

services, which couples dual-core Itanium processors

with Xilinx Virtex-4 devices. The SGI RASC core

contains 5 SRAM banks with a combined capacity of

a few hundred MBs of storage. This would severely

limit the size of matrices which can be handled, un-

less there is a provision for feeding data to the SRAM

banks from the host machine. The time required for

these transfers would have to be factored in the per-

formance. Scaling the computational cores upwards

would increase these communication costs. How-

ever, the design achieves a remarkable 99% of the

peak (1600 MFLOPS) for certain matrices. The de-

sign uses double-buffering technique for storing vec-

tor, matrix (CRS format) and partial sum elements in

local on-chip FPGA fabric memories. The design also

interleavesdot productcomputations of differentrows

to prevent RAW hazards in the accumulator pipeline.

However, the rows are not distributed amongst dif-

ferent processors, which might not result in optimal

workload distribution.

The architecture implemented by Sun (Sun et al.,

2007) is aimed for implementation on Virtex-II Pro

device as an accelerator on host machines like Cray

XD-1. The design can be conﬁgured to have dif-

ferent data widths for input and output, for integer

data. This would increase bandwidth utilization. The

system used for estimating performance, uses QDR

RAM (SRAM) of size of the order of few MBs (16

MB). However, using SRAMs for storage, the design

is able to achieve more than 95% of peak performance

on most matrices at operating frequency of the order

of 175 MHz.

GPUs (Bell and Garland, 2008) do present a

performance beneﬁt, but at the cost of high power

consumption. For the unstructured matrices arising

in economics, circuit simulation, GPUs give perfor-

mance of 2-4GFLOPS for double precision data.

3 OVERVIEW

Since SpMxV for large matrices cannot be handled

exclusively using on-chip memories, we propose a

hybrid system wherein the matrix and vector are

stored in external off-chip commodity DRAMs and

the data is cached in local on-chip memories. Since

burst accesses can help to hide DRAM latencies,

the following sections explain a processing paradigm

which enables data to be stored in a fashion amenable

to burst accesses.

Practically encountered matrices are not patholog-

ically sparse nor are they perfectly clustered, both

properties are present in them to varying degrees. We

propose that matrices be split accordingly. Clustered

non-zeros are handled by one kernel, and the outliers

by a differentone. In this paper we design an architec-

ture best suited to process the clustered blocks of non-

zeros. Since the outliers are few in number and ran-

domly arranged, they should be handled separately.

A point to note is that, the proposed design does not

aim to accelerate computation for any speciﬁc matrix

structure.

3.1 Matrix Blocking

The operationinvolving sparse matrix vector multipli-

cation is distributed amongst multiple processing ele-

ments. Since maximum throughput will be obtained

when all the processing elements are operating in par-

allel, the vector access should be as fast and conﬂict-

free as possible for each processing element.

The local (single-cycle access) BRAM storage in

FPGAs is not sufﬁcient to store multiple instances of

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

478

a multi-million double precision vector. To tackle

this problem the dense matrix is divided into square

‘dense’ blocks of certain predetermined size. A ma-

trix block size of 128×128 is small enough to allow

for multiple on-chip caches and also contains sufﬁ-

cient non-zero elements. The block size could be

changed with no fundamental changes to the rest of

the design. Since we are using external DRAMs for

matrix and data storage, we aim to make maximum

use of the burst accesses of DRAM to hide the access

latencies. As described in previous paragraph, since

matrix elements are stored in the order in which they

are to be processed, matrix data can be fetched in con-

tinuous stream of bursts.

Only the ‘dense’ blocks are given as input to the

processing elements in a row-major fashion. A row-

strip is deﬁned to be the set of all the blocks (128n row

aligned) having the same set of rows. A direct fall-

out of such a mechanism is that the vector too can be

blocked and thus only elements in required blocks of

the vector can be fetched using burst accesses rather

than the whole vector being stored. Moreover, we

pre-fetch the next required vector block to reduce

stalls in computation, which is instrumental in hid-

ing the DRAM access latencies. Since the blocking

is very ﬁne, the vector block size is small and thus

the vector entries can easily be replicated in the local

storage of all processing elements, bypassing prob-

lems which may arise due to memory contention.

3.2 Dataﬂow

The matrix data is arranged in blocked column-row-

data format in the DRAM attached to each process-

ing element. During operation, ‘dense’ matrix blocks

are processed in a row major fashion one after the

other by streaming the complete matrix word from

DRAM into the processing element. The matrix data

in each block is distributed amongst different process-

ing elements in the pre-processing phase. All pro-

cessing elements operate on the same block at any

given time. For each ‘dense’ matrix block, the pro-

cessing elements compute the product of each matrix

element assigned to it and the appropriate vector el-

ement using the vector block replicated in each pro-

cessing element. Each processing element also main-

tains a 128 element (one for each row in block) partial

sum array, which is re-initialized to zeros at the start

of processing of a rowstrip. In each processing ele-

ment, the generated product is accumulated into that

element of these partial sum arrays corresponding to

the row of the matrix data. These partial sum arrays

are transferred out of each processing element at end

of processing of a rowstrip, after which they are ac-

cumulated in a adder tree. Thus, for each row in the

rowstrip, we get the accumulated sum which is the

corresponding row element in the result vector. This

operation is described in a scaled down example, hav-

ing two processing elements, in ﬁgure 1. In the ﬁgure,

the variable Y

ijk

represents that it is a element con-

tributing to the result vector generated by processing

element i, for row k of block j of the matrix. The

grayed blocks represent ‘dense’ blocks and numbers

represent the processing element the matrix element

is assigned to.

Figure 1: SpMxV operation.

4 DESIGN

A block diagram of the processing element is shown

in ﬁgure 2. Modules in the ﬁgure are explained in the

following section.

4.1 Vector Cache

The vector blocks which are fetched from the DRAMs

in burst accesses are replicated in the local vector stor-

age of each processing element. FPGAs have single-

cycle Block RAMs (BRAMs) which are used for im-

plementing these memories. Since the matrix is di-

vided into block sizes of 128, we need storage for

128 elements of the block currently being processed

as well as the 128 pre-fetched vector elements corre-

sponding to the next matrix block. By using simple

dual port memories, while vector elements are being

read from one half of the storage by the processing

elements, vector elements corresponding to the next

block are pre-fetched in the other half. Thus we effec-

tively utilize double-buffering technique to hide ac-

cess latencies.

Input vector blocks are stored in order which en-

sures that the result vector needs minimal manipula-

tion. This scenario has advantage of result storage

DOUBLE PRECISION SPARSE MATRIX VECTOR MULTIPLICATION ACCELERATOR ON FPGA

479

Figure 2: Block Diagram of processing element.

and the disadvantage of random input access. How-

ever, the knowledge of the sequence of access of vec-

tor blocks is static and can be provided to the vec-

tor fetching units at initialization time, reducing the

penalty for random block access making the second

scenario more feasible than the ﬁrst for iterative ap-

plications. Moreover within a block, the vector data

elements are sequentially stored, which ensures that

data can still be accesses in burst.

4.2 Floating Point Multiplier

A fully IEEE-754 compliant double precision ﬂoating

point multiplier, generated using Xilinx CoreGenera-

tor was used in the design. The multiplier (Coregen

IP v4.0) is deeply pipelined for high throughput, is

10-stage pipelined and requires 13 DSP48E slices.

4.3 Floating Point Adder

A fully IEEE-754 compliant double precision ﬂoat-

ing point adder, generated using Xilinx CoreGenera-

tor was used in the design. The adder is pipelined for

high throughput. However, since the adder functions

as an accumulator, there is a loop from adder output

to adder input through local partial sum memory. This

has the potential to cause RAW hazards, since the

adder might try to read from an address whose valueis

still in the pipeline and this not been updated. Hence

we would not want the pipeline to be very deep, as

this would compromise on the efﬁciency of operation

and offset the advantage offered by deeper pipelining.

The adder (Coregen IP v4.0) is 14-stage pipelined and

requires 3 DSP48E slices.

4.4 Partial Sum Storage

Since we process the matrix in blocks of 128×128,

we need storage for 128 partial sums in each process-

ing element, each corresponding to one of the 128

rows in the block being processed. When processing

for a row strip is done, the partial sums correspond-

ing to that row strip need to be transferred out of the

processing element. This would take as many clock

cycles as the depth of the partial sum storage. If we

have only one buffer for storing partial sums, the en-

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

480

Figure 3: Embedded System Schematic.

tire processing pipeline will have to halt while this

transfer is in progress. To prevent such situations, as

in the case of the vector storage, we have a double-

buffered memory system for storing the partial sums

generated by each processing element. This ensures

that the accumulator does not have to stall while the

partial sums are being read out of the processing ele-

ment at the end of a row strip. Since each processing

element can potentially generate 128 partial sums, the

size of the storage buffer is enlarged to 256 elements.

While the accumulator reads as well as writes to

one of the ping-pong memory buffers in the storage,

the other buffer is simultaneously being emptied and

initialized to zero. Thus during certain periods of op-

eration more than two ports are needed. A simple

dual-port memory, as used for vector storage or even

a true dual-port memory provides only two ports. As

a result, we need two simple dual port memories serv-

ing as separate storage buffers, each of 128 elements

as opposed to one big buffer of 256 elements.

4.4.1 Pipeline and Control

We have two pipelines separated by an isolation

queue. The ﬁrst pipeline comprises of vector access

stage (4 stages), multiplier stage (10 stages) and the

second comprises of the partial sum access stage (2

stages) and adder stage (14 stages). The pipeline

serves as a delay mechanism (using shift registers)

for the address pointers so that they are available at

the right time in different stages of the computation

pipeline. This unit also contains pipeline stall control

logic.

5 SYSTEM IMPLEMENTATION

As a proof of concept, we implemented the process-

ing element as a prototype accelerator peripheral in

an embedded system. The Gauss-Jacobi iterative al-

gorithm (Golub and Loan, 1996) is the application

chosen for acceleration using the sparse matrix vector

multiplication processing element described in sec-

tion 4. Typically, in most iterative methods, and

Gauss-Jacobi is no exception, operations other than

sparse matrix vector multiplication have structured

accesses. These operations can be efﬁciently per-

formed by a simple off-the-shelf micro-processor in

conjunction with a cache. In the following sections,

the embedded system comprising of a soft proces-

sor and peripheral units such as DDR2 DRAM con-

troller, DMA controller, interrupt controller and bus

controller is described.

5.1 System Description

The embedded system is developed around the 32-bit

DOUBLE PRECISION SPARSE MATRIX VECTOR MULTIPLICATION ACCELERATOR ON FPGA

481

MicroBlaze processor, a soft processor provided by

Xilinx along with the proprietary embedded develop-

ment kit. The processor is conﬁgured to operate at

125 MHz and have 64KB data cache. The board used

for prototyping, Xilinx XUPV5-LX110T also incor-

porates a 256 MB DDR2 SDRAM module which pro-

vides the system with the capability to handle large

matrices.

A DMA controller is included to facilitate burst

transfers of data from DRAMs to processing element.

The DMA can be conﬁgured to have variable inter-

nal storage, and variable read and write burst sizes.

To hide DRAM latencies, DMA is conﬁgured to have

read and write burst size of 16 which is the maximum

supported by the peripheral.

The system has the processing element as well as

the DMA for interrupt sources. Since the processor

has only one interrupt line, an interrupt controller is

included to enable processor to respond to interrupt

requests as well as prioritize the requests. The pro-

cessing element generates three types of interrupts -

request storage of result vector block, request input

vector block and request matrix data. The DMA gen-

erates an interrupt to indicate transfer completion.

The peripherals are connected to the processor us-

ing PLB (Peripheral Local Bus) which has a width of

32, operates at 125 MHz and can support burst trans-

fers. A seperate link - Xilinx Cache Link - between

the processor and the DDR2 DRAM memory con-

troller is also included to support caching of DRAM

data.

Figure 3 shows a schematic of the embedded sys-

tem.

5.2 Hardware and Software

Development

Each of the three interfaces - matrix, vector and partial

sum transfer interfaces - generates an interrupt sig-

nal requesting transfer of data and then communicates

with the software till the end of the transaction. In this

section, control ﬂow in both hardware and software is

explained side by side.

The hardware state machines controlling the inter-

faces, after generating the interrupt, wait for acknowl-

edge, then mask the interrupt signal and wait for

the transfer complete notiﬁcation after which they go

back to their initial state. Interrupt acknowledge and

DMA transfer are multi-cycle processes and thus the

hardware state machines have no information about

their progress. They will keep on interrupting the pro-

cessor even after interrupt has been acknowledged,

if there is no communication between software and

hardware.

Hence for each interface, the software controls a

pair of signals - interrupt acknowledge and transfer

done - represented as bits in a programmervisible reg-

ister, which initially represent false condition. When

an interrupt is received, software clears the transfer

done signal and only then sets interrupt acknowledge.

This ensures that transfer done signal set high for the

previous transfer is not interpreted by the hardware

state machine for the current transfer. After the DMA

signals end of transfer, ﬁrst interrupt acknowledge is

cleared and only then transfer done is set. This is es-

sential because a register write by software is a multi-

cycle process. If transfer done is set before clear-

ing interrupt acknowledge, and an interrupt request

is generated in between, the hardware state machine

would interpret the acknowledge for the most recent

interrupt.

The rest of the application software follows the

following ﬂowchart as depicted in ﬁgure 4.

However such an embedded system has certain

limitations which are enumerated below.

1. The soft processor available is a 32-bit processor.

This decreases bus width to 32 bits, in turn de-

creasing the bandwidth available to the process-

ing element. Multiple clock cycles are required to

transfer just one matrix/vector/result word.

2. A single processor embedded system can contain

only one bus. Requests to the DRAM have to be

made on the same bus on which the DRAM pro-

vides data. Firstly, this reduces throughput since

requests cannot be queued. Secondly, this will in-

crease number of bus turnarounds.

3. The board provides only one DRAM interface

thus decreasing number of processing elements

supported and imposing need to time-multiplex

transfers.

4. The DMA controller module makes requests for

maximum burst size of 16. Such a small burst is

not sufﬁcient to hide DRAM access latency.

5. Data is transferred from source to internal DMA

storage, and then transferred from the DMA stor-

age to the destination. Thus data needs to be trans-

ferred twice along the same bus. The time re-

quired for bus turnaround worsens the situation.

However, this problem can be alleviated by in-

cluding a bus master unit in the PLB interface.

6 CONCLUSIONS

In this paper an approach for embedded system de-

sign for sparse matrix-vector multiplication using the

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

482

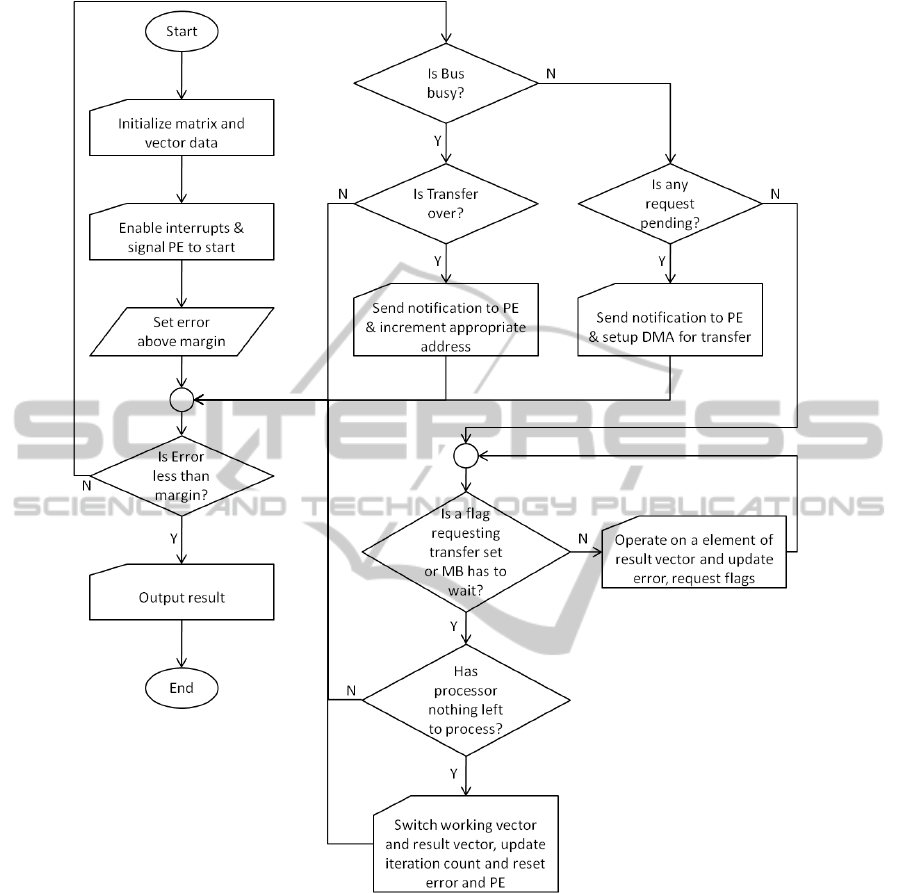
Figure 4: Software Flow.

MicroBlaze platform by Xilinx, is presented and dis-

cussed. The paper discusses the trade-offs for the Sp-

MxV architecture, it aims to provide insight into the

design of accelerators. The simplicity of the design

and the use of commodity DRAMs makes this design

a practical accelerator.

REFERENCES

Bell, N. and Garland, M. (2008). Efﬁcient sparse matrix-

vector multiplication on CUDA. NVIDIA Technical

Report NVR-2008-004, NVIDIA Corporation.

Davis, T. and Yu, H. (2010). The university of ﬂorida sparse

matrix collection. http://www.cise.uﬂ.edu/research/

sparse/matrices/.

deLorimier, M. and DeHon, A. (2005). Floating-point

sparse matrix-vector multiplication for fpgas. FPGA

2005: Proceedings of the 2005 ACM/SIGDA 13th in-

ternational symposium on Field-programmable gate

arrays, pages 75–85.

Golub, G. H. and Loan, C. F. V. (1996). Matrix Computa-

tions. Johns Hopkins University Press, 3 edition.

Gregg, D., McSweeney, C., McElroy, C., Connor, F.,

DOUBLE PRECISION SPARSE MATRIX VECTOR MULTIPLICATION ACCELERATOR ON FPGA

483

McGettrick, S., Moloney, D., and Geraghty, D.

(2007). Fpga based sparse matrix vector multipli-

cation using commodity dram memory. FPL, pages

786–791.

Kuzmanov, G. and Taouil, M. (2009). Reconﬁgurable

sparse/dense matrix-vector multiplier. Proceedings of

the International Conference FPT 2009, pages 483–

488.

Morris, G. R. and Prasanna, V. (2007). Sparse matrix com-

putations on reconﬁgurable hardware. Computer, vol

40, no 3, pages 58–64.

Morris, G. R., Prasanna, V. K., and Anderson, R. D.

(2006). A hybrid approach for mapping conjugate gra-

dient onto an fpga-augmented reconﬁgurable super-

computer. FCCM ’06: Proceedings of the 14th An-

nual IEEE Symposium on Field-Programmable Cus-

tom Computing Machines, pages 3–12.

Sun, J., Peterson, G., and O.O, S. (2007). Mapping sparse

matrix-vector multiplication on fpgas. Proc. Recon-

ﬁgurable Systems Summer Inst. (RSSI).

Williams, S., Oliker, L., Vuduc, R., Shalf, J., Yelick, K., and

Demmel, J. (2007). Optimization of sparse matrix-

vector multiplication on emerging multicore plat-

forms. SC ’07: Proceedings of the 2007 ACM/IEEE

conference on Supercomputing, pages 1–12.

Zhuo, L. and Prasanna, V. (2005). Sparse matrix-vector

multiplication on fpgas. FPGA 2005: Proceedings of

the 2005 ACM/SIGDA 13th international symposium

on Field-programmable gate arrays, pages 63–74.

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

484