MULTI-ROBOT DECENTRALIZED EXPLORATION USING A
TRADE-BASED APPROACH
Zhi Yan, Nicolas Jouandeau and Arab Ali Cherif
Advanced Computing Laboratory of Saint-Denis (LIASD), Paris 8 University
2 Rue de la Libert´e, 93526 Saint-Denis, France
Keywords:
Coordinated exploration, Decentralized decision making, Multi-robot systems.
Abstract:
This paper addresses the problem of exploring an unknown environment by a coordinated team of robots. An
important question is, which robot should explore which region? In this paper, we present a novel decentralized
task allocation approach based on trading rules for multi-robot exploration. In the decentralized system, robots
can make their own decisions according to the local information with limited communication. In contrast to
previous approaches, our trade-based approach is designed to simulate the relationship between buyers and
sellers in a business system, to achieve dynamic task allocation by using a mechanism of unsolicited bid. Our
approach has been implemented and evaluated in simulation. The experimental results demonstrate a good
performance of the proposed trade-based approach compared to previous approaches.
1 INTRODUCTION
Exploration of an unknown environment is a funda-
mental problem in robotics. It requires an agent to
cover the unknown area while building a model of the
environment from sensor data so as to achievethe pur-
pose of exploration. This research can be used in a
wide range of applications such as planetary mission,
automated surveillance, and search and rescue opera-
tions.
Compared with single agent, using multiple
agents has a number of potential advantages (Cao
et al., 1997), (Dudek et al., 1996). For example, a
team of robots is able to complete an exploration mis-
sion faster than a single robot. The key to gain the
advantages is coordination. Without coordination, it
will not only lower mission efficiency, but also lead
to the failure of the entire mission in extreme cases.
The core of coordination is task and role allocation.
In other words, we need to answer such a question:
which agent should execute which task (Gerkey and
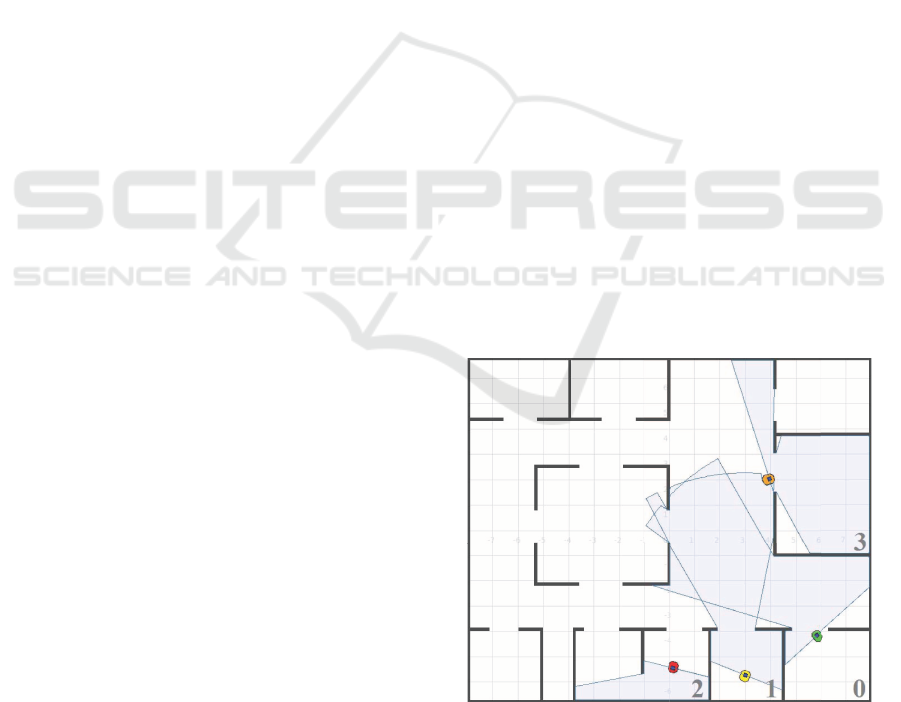
Matari´c, 2004)? Figure 1 shows an example of multi-
agent coordination. Four robots explore an unknown
environment cooperatively. The result of task alloca-
tion is that different robots are responsible for explor-
ing different rooms. There are generally two types
of mechanisms for task allocation, centralized and
decentralized. The advantage of centralized mecha-
nism is that the optimal plans can be found. Never-
Figure 1: Four robots explore an unknown environment co-
operatively. The green robot has completed the exploration
of room 0, is moving to next room. The yellow robot is ex-
ploring room 1. The red robot is exploring room 2, and the
orange robot is moving to room 3.
theless, this mechanism is ineffectual for large teams
with more agents. There is no central planner in the
decentralized mechanism. Robots use locally observ-
able informations to make their plans. This mecha-
nism has a good adaptability and strong robustness,
but the solutions it got are often sub-optimal.
In this paper, we consider the problem of explor-
ing an unknown indoor environment with a homo-
99
Yan Z., Jouandeau N. and Ali Cherif A..
MULTI-ROBOT DECENTRALIZED EXPLORATION USING A TRADE-BASED APPROACH.
DOI: 10.5220/0003405800990105
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 99-105
ISBN: 978-989-8425-75-1
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

geneous team of robots. The larger context of this
problem is multi-robot search and rescue in danger-
ous environments such as fire and explosion. The ob-
jective of the research is to explore the entire environ-
ment, while minimizing the time needed to complete
the overall exploration. In fact, this is also an im-
portant prerequisite to better searching and rescuing.
Moreover, the realizations of search and rescue are
not within the scope of this paper.
This paper presents a novel approach of decentral-
ized dynamic task allocation based on trade rules for
groups of robots. This approach is designed to sim-
ulate the relationship between buyers and sellers in a
business system. The robot which plays the role of
buyer applies for a task, and the robot which plays
the role of seller is responsible for the assignment of
tasks. Due to the context of search and rescue, the
following three issues should be considered while de-
signing our trade-based approach:
• Useability, it means that robots are able to imple-
ment the proposed approach easily, and use fewer
computer system resources.
• Efficiency, it means that robots are able to handle
the assignment of tasks with as little communica-
tion as possible.
• Robustness, it means that robots are able to make
their own decisions correctly in the absence of
teammates’ information.
In contrast to previous research, especially the
well known auction method (Gerkey and Matari´c,
2002), our approach uses a application/allocation
model unlike the traditional auction/bidding model.
The buyer makes a request of task allocation to the
seller, we called it the unsolicited bid mechanism. Af-
ter a period of time, the seller analyzes the received
requests, then assigns the tasks to the buyers reason-
ably. An obvious characteristic of our approach is that
it has the ability to assign multiple tasks to multiple
robots at a time.
This paper is organized as follows. In Section 2,
we give an overview of some related works. Subse-
quently, we briefly discuss the requirements of indoor
exploration in Section 3. Then we present our trade-
based approach in Section 4. Finally, we describe
the experimental results obtained with our approach
in Section 5.
2 RELATED WORK
The problem of exploring an unknown environment
by a team of mobile robots has received increasing
attention in the past few years.
Yamauchi (Yamauchi, 1998) presented a cooper-
ative, decentralized and fault-tolerant multi-robot ex-
ploration strategy based on the concept of frontiers.
Frontiers are regions on the boundary between open
space and unexplored space. In his approach, robots
share perceptual information, but maintain separate
global maps. Each robot makes its own decisions
about where to navigate. Whenever a robot arrives at
a new frontier, it sweeps its sensors and constructs a
local evidence grid representing its current surround-
ings. This local grid is integrated with the robots
global grid, and also broadcast to all of the other
robots. However, different robots may go to explore
the same frontier in this system, then the efficiency of
exploration will be lowered for this cause.
Burgard, Moors, Fox, Simmons and Thrun (Bur-
gard et al., 2000) designed a coordination component
based on the approach of Yamauchi. This component
applies a probabilistic method which takes the cost of
reaching a frontier and its utility into account simulta-
neously. The cost is given by the distance of traveling
to a frontier (by using value iteration algorithm) and
the utility is given by the size of the unexplored area
that a robot can cover from this frontier with its sen-
sors. Whenever a frontier is assigned to a robot, the
utility of the visible unexplored area of this frontier is
reduced to all of the other robots, so that the problem
of more than one robot go to the same frontier should
no longer appear. However, a central agent is required
for this approach. If the central agent fails, the whole
system will fail.
Gerkey and Matari´c (Gerkey and Matari´c, 2002)
proposed an auction-based task allocation approach
for decentralized multi-robot coordination. The auc-
tion proceeds in five steps: task announcement, met-
ric evaluation, bid submission, close of auction and
progress monitoring/contract renewal. This strat-
egy has been implemented and tested in a general
task allocation system called MURDOCH, which is
built upon a principled, resource centric and pub-
lish/subscribe communication model. However, their
method requires a high amount of data communica-
tion. This not only increases the load of system, but
also influences the robustness of system.
Zlot, Stentz, Dias and Thayer (Zlot et al., 2002) in-
troduced a market-based task allocation approach for
multi-robot exploration. This technique borrows the
market architecture which seeks to maximize bene-
fit while minimizing cost, thus aiming to maximize
utility. The benefit is information gained by visit-
ing a goal point, the cost is the estimated distance
traveled to reach the goal (by using D* algorithm),
then the utility is the difference between the benefit
and the cost. Similar to the auction-based strategy,
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
100

the market-based strategy also use the auction/bidding
model. However, this approach also requires a high
amount of data communication.
Wurm, Stachniss and Burgard (Wurm et al., 2008)
proposed a technique for coordinating a team of
robotic explorers by using a segmentation of envi-
ronment. Instead of considering frontiers between
unknown and explored areas as target locations, this
method takes the structure of the environment into
account, and segments the already explored environ-
ment based on Voronoi diagram of map, then assigns
each robot to a separate segment with a task to explore
corresponding area by using the Hungarian algorithm.
Their experiments show a significant improvement of
the segmentation-based approach compared to a stan-
dard frontier-based approach for structured indoor en-
vironments. This is favourable for explorations in
dangerous environments. However, Their technique
still requires a central planning component to commu-
nicate with all teammate robots and handle the distri-
bution of tasks.
Marjovi, Nunes, Marques and de Almeida (Mar-
jovi et al., 2009) presented an approach for coopera-
tive multi-robot exploration, fire searching and map-
ping in an unknown environment, which aims to mini-
mize the overall exploration time while making it pos-
sible to localize fire sources in an efficient way. In
their approach, a decentralized frontier-based explo-
ration method is used for evaluating the ratio between
cost (by using A* algorithm) and utility to navigate
to target waypoints. A potential field method is used
for controlling the robots’ motion to avoid obstacles,
and a triangulation method is used for identifying fire
sources. However, the amount of coordination of this
approach is limited and a high amount of data com-
munication should be required.
Besides, there are some other approaches devel-
oped with various policies (Rekleitis et al., 2000), (Ko
et al., 2003), (Stachniss et al., 2009).
In our previous work (Yan et al., 2010), we consid-
ered the problem of multi-robot exploration by using
separate topological graph. This work aims to solve
the waiting situations like congestion or collision dur-
ing robot motion planning. If all the robots use the
same topological graph, then they might follow the
same exploration path, so that causes the problem of
waiting situations. We proposed an approach based
on sampling environment map iteratively to support
the efficiently coordinated multi-robot exploration.
However, this approach needs a centralized planner
to process the map and assign target points to robots.
Therefore, in this paper, we study how to design an
useable, efficient and robust decentralized system on
the one hand, and we still take the structure of envi-
ronment to ensure the efficiency of exploration into
account on the other hand.
3 INDOOR EXPLORATION
Our focus in this paper is on indoor environment ex-
ploration. Indoor environments are generally struc-
tured environments. For the search and rescue sce-
nario, if the structure of the environment is taken into
account, the efficiency of exploration will be greatly
improved. Therefore, in our approach, we assume that
all robots share a joint occupancy grid map with infor-
mation about the structure of environment, which is
generated from robots’ sensor readings. In addition,
unlike outdoor exploration, it is difficult for robots lo-
calize themselves by using the GPS module in indoor
environment, so in our implementation, the robot uses
odometry for self-localization.
4 TRADE-BASED APPROACH
A business system is mainly made up of buyers and
sellers. The relationship between them is known as
exchange relation. Buyers can use money to purchase
goods or services from sellers, then sellers collect
money and sell goods or services to buyers. Our ap-
proach in this paper is built on the simulation of this
relationship, the model is as follows:
Trade =< R, M, T, P,C > (1)
where R represents the mobile robots. M represents
the whole mission to be completed, which consists of
several tasks, M = {m
0
, m
1
, .. . , m
n
}. T represents the
time needed (i.e. the benefit obtained) to complete the
whole mission. P signifies the task allocation plan. C
signifies the set of cost to complete the whole mis-
sion, C = {c
0
, c
1
, .. . , c
n
}. In fact, to each robot, the
entire planning contains three steps: role allocation,
task allocation and motion planning.
4.1 Role Allocation
The role allocation is to solve the problem of which
robot should be buyer and which robot should be
seller. As far as a homogeneous mobile robot team
is concerned, robots themselves have no preference
for role. Therefore, a simple and effective way is to
number the robots in the team. Robot can broadcast
its number when it is not in task, then evaluates the
received numbers after a period of time. If there is a
number smaller than its own, then the robot will play
MULTI-ROBOT DECENTRALIZED EXPLORATION USING A TRADE-BASED APPROACH
101

the role of buyer. The details of our implementation
are given in Algorithm 1.
Algorithm 1: Trade-based role allocation for robot r.
1: if robot r is not in task then
2: broadcast its number r
3: if time < timeMax then
4: receive messages
5: time ← time+ 1
6: else
7: robot ← seller
8: for each received number r
′
do
9: if r
′
< r then
10: robot ← buyer
11: break
12: end if
13: end for
14: end if
15: end if
It is worth noting that the difference between
buyer robot and seller robot is just in function, and
only temporary. The buyer at this moment in a task
could become the seller in another task in the next
moment.
4.2 Task Allocation
Once the idle robot has determined its own role, it
should enter the task allocation phase. For the buyer
robots, the first thing to do is to choose a task to
bid for and estimate the cost required to complete the
task. The task is to explore an unknown region which
can be identified by topologizing the grid map of the
environment (Wurm et al., 2008), (Yan et al., 2010).
The robot is capable to extract critical points (Thrun,
1998) for a given map to distinguish corridors, door-
ways and rooms. The cost metric can be various, such
as distance traveled, time taken or energy expended.
In this paper, we use the distance traveled as the cost
metric. As a result, the robot will calculate the dis-
tance between its current position and target position
(for example, a critical point) as the estimated task
cost by using the wavefront propagation algorithm
(LaValle, 2006):
c
m
r
= wave front(pos(r), pos(m)) (2)
where c
m
r
represents the estimated cost c for robot r to
complete the task m. After completing the cost esti-
mate, the buyer robot should send a purchase request
to seller robot for the new task. We called this model
the unsolicited bid mechanism. The purchase mes-
sage mainly contains three information:
pums
r
= {r, m, c} (3)
where pums
r
represents the purchase message pums
sent by buyer robot r, r in the message means the
number of the buyer robot, m signifies the identifier
of the task, and c denotes the estimated task cost c
m
r
.
After the bidding process, the buyer robot will receive
a message on whether to get the task from the seller
robot or not. If the buyer robot gains the bidden task,
it will enter into the motion planning process. Other-
wise, it will return to the role allocation process for
a new task. A detailed decision making flowchart is
given in Figure 2.
For the seller robot, homoplastically, the first step
is to select a task and estimate the cost. Then it
should collect the purchase message from the buyer
robots within a given bidding period. After this pe-
riod, the seller robot will stop receivingpurchase mes-
sage and evaluate the purchase requisitions, then as-
sign the tasks to each buyer robot for reasonably. The
detailed decision making flowchart for seller robot is
illustrated in Figure 3. Task allocation is performed
by using a greedy algorithm. That is, always select-
ing the robot with lower estimated cost as the object
of task distribution. The implementation details are
given in Algorithm 2.
Algorithm 2: Trade-based task allocation for seller
robot.
1: a.init()
2: for all received task requests m in purchase mes-
sage pums do
3: if there is a same task m
′
in the allocation table
a then
4: if m.cost < m
′
.cost then
5: a.update(m
′
)
6: end if
7: else
8: a.add(m)
9: end if
10: end for
The task allocation message sent to buyer robot
mainly includes two information:
tams
r
= {r, m} (4)
where tams
r
represents the task allocation message
tams sent by seller robot r, r in the message means the
number of the seller robot, m signifies the identifier of
the task. It is worth noting that, in fact, the seller robot
itself is also the object of task allocation.
The robot which has completed a task will update
its task list, and also broadcast to all teammates.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
102
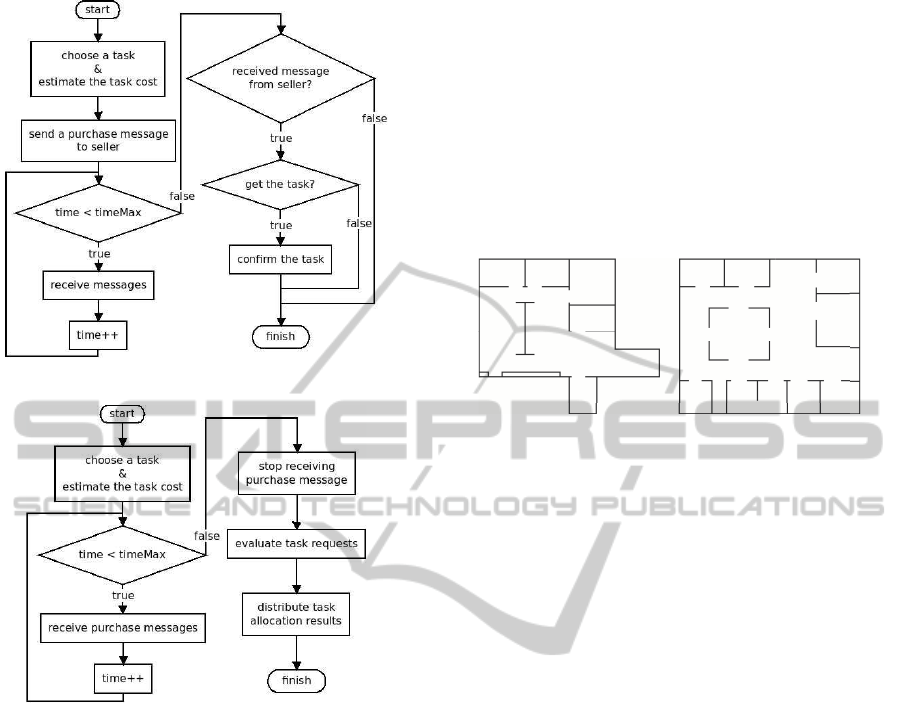
Figure 2: Decision making flowchart for buyer robot.
Figure 3: Decision making flowchart for seller robot.
4.3 Motion Planning
The motion planning process is in charge of the im-
plementation of task, i.e. the exploration of the un-
known region. In our approach, the mobile robots will
share an occupancygrid map with respect to the struc-
ture of the environment during their exploration mis-
sion. This map is used for path planning and obsta-
cle avoidance in real time. Consequently, we use the
wavefront propagation algorithm (LaValle, 2006) for
global path planning and the vector field histogram al-
gorithm (Ulrich and Borenstein, 1998) for goal seek-
ing and local obstacle avoidance.
5 EXPERIMENTS
Our approach has been implemented and evaluated in
Stage (Gerkey et al., 2003) a 2.5D multiple-robotsim-
ulator. The simulation experiments were conducted
by using a group of Pioneer 2-DX robot equipped
with a laser range finder which can provide 361 sam-
ples with 180 degrees field of view and a maximum
range of 8 meters. Each robot can localize itself based
on an abstract localization device which models the
implementation of SLAM. The ratio between real-
world time and simulation time is about 1:3. All ex-
periments reported in this paper were carried out on a
system with an Intel Core 2 Duo E8400 3.00GHz pro-
cessor, an Intel Q43 Express chipset and two DDR2
800MHz 1024MB dual channel memory.
Figure 4: Two environment maps used in our simulation:
map A (left) and map B (right).
To evaluate our trade-based approach, we used
a different number of robots to conduct several ex-
periments in various environments. We also com-
pared our approach to a centralized approach based
on the Hungarian method (Kuhn, 1955) in which the
task allocation is done by a central planner. Figure
4 depicts two maps used in our simulation which are
enclosed spaces with 14 meters long and 16 meters
wide. Both of them are indoor structured environ-
ments. The screenshot of our implementation can be
seen in Figure 1, and the results of our experiments
are given in Table 1 and Table 2.
Table 1 shows a comparison of the results be-
tween our trade-based approach (decentralized) and
the Hungarian-based approach (centralized) in map
A with the context of measuring the exploration run-
time. Each set of data in the table contains an average
time (in seconds) of 10 runs and its standard deviation
in parentheses. The Hungarian method is an efficient
way to find an optimal solution for a task assignment
problem. In our experiment, this procedure is used as
a reference for measuring the performance of our pro-
posed method. Table 1 indicates that, the difference
on completion time between trade-based exploration
and Hungarian-based exploration is 6.6% (4.3 sec-
onds) for 2 robots, 19.4% (8.9 seconds) for 3 robots,
and 3.9% (1.8 seconds) for 4 robots respectively.
Table 2 shows the results for map B. The run-
time difference is 6.3% (4.5 seconds) for 3 robots and
7.4% (4.6 seconds) for 4 robots respectively. More-
over, we observed that, our trade-based approach
gained 14.2% time (13.9 seconds) compared to the
Hungarian-based approach with 2 robots. It reflects
MULTI-ROBOT DECENTRALIZED EXPLORATION USING A TRADE-BASED APPROACH
103

Table 1: Exploration Runtime Comparison for Map A.
Hungarian-based Trade-based
exploration exploration
2 robots 65.20s (1.166) 69.50s (0.806)
3 robots 45.90s (0.538) 54.80s (1.887)
4 robots 45.90s (7.120) 47.70s (0.458)
Table 2: Exploration Runtime Comparison for Map B.
Hungarian-based Trade-based
exploration exploration
2 robots 112.0s (3.317) 98.10s (1.300)
3 robots 71.70s (1.487) 76.20s (3.027)
4 robots 61.80s (1.249) 66.40s (1.020)
NP-hard of multi-robot exploration from one side.
With Table 1 and Table 2, we found that, although
our trade-based approach requires more time com-
pared to the Hungarian-based approach in most cases,
the difference is quite acceptable. Consequently, the
experimental results still reflect a good performance
of our proposed approach.
Another experiment was conducted to evaluate the
robustness of our method. The point is to test the ef-
fect of decision making of a robot under uncertainty
caused by information loss. The motivations of the
loss may be damage of robot components, communi-
cation obstacles (distance), or difficult circumstances.
For a coordinatedrobots team with a decentralizedde-
cision making system, each robot in the team need to
exchange information with its teammates. The prob-
lem of information loss will influence the decision
performance. Table 3 and Table 4 show the robust-
ness testing results of our proposed method in map A
and map B respectively, in which we varied the prob-
ability of information loss with 10%, 30% and 50%.
Each set of data in the tables contains an average time
(in seconds) of 10 runs.
Table 3 shows that, in map A: Under 10% infor-
mation loss, the system keeps a good performance,
the exploration runtimes are prolonged but still close
to the normal results, the differences between them
are 0.9 seconds (2 robots), 1.4 seconds (3 robots) and
3.1 seconds (4 robots). Under 30% information loss,
the performance of system was lowered, the explo-
ration runtimes are prolonged by the undesirable ef-
fect of the loss. Compared with the normal results, the
differences are 15.0 seconds (2 robots), 8.2 seconds
(3 robots) and 12.0 seconds (4 robots). Under 50%
information loss, the performance of system keeps
lowering, and the differences between the exploration
runtimes and the normal results are 15.6 seconds (2
Table 3: Robustness Testing with Map A.
Information loss probability
10% 30% 50%
2 robots 70.40s 84.50s 85.10s
3 robots 56.20s 63.00s 76.80s
4 robots 50.80s 59.70s 73.90s
Table 4: Robustness Testing with Map B.
Information loss probability
10% 30% 50%
2 robots 100.3s 141.3s 155.2s
3 robots 82.00s 102.5s 124.6s
4 robots 67.00s 83.00s 92.80s
robots), 22.9 seconds (3 robots) and 26.2 seconds (4
robots).
Table 4 shows that, for map B: Under 10% infor-
mation loss, the differences are 2.2 seconds (2 robots),
5.8 seconds (3 robots) and 0.6 seconds (4 robots)
compared with normal results. Under 30% informa-
tion loss, the differences are 43.2 seconds (2 robots),
26.3 seconds (3 robots) and 16.6 seconds (4 robots).
Under 50% information loss, the differences are 57.1
seconds (2 robots), 48.4 seconds (3 robots) and 26.4
seconds (4 robots).
With Table 3 and Table 4, we found that, multi-
robot coordination depends on the information ex-
change between teammate robots, the exploration
runtimes are prolonged for the probability of infor-
mation loss. Moreover, the corresponding incre-
ments are considered acceptable in our experiments.
This demonstrates a good robustness of our proposed
trade-based approach. In fact, our approach still work
in extreme cases (zero communication), but the effi-
ciency is lower.
6 CONCLUSIONS
In this paper, we presented a novel task allocation
approach under decentralized coordination for multi-
robot exploration. The basic thought of the proposed
approach is to simulate the relationship between buy-
ers and sellers in a business system, and dynamically
allocate the task by using an unsolicited bid mecha-
nism. Typically, the procedure goes like this: At first,
we should determine the role of the robots, i.e. buyer
or seller, this step is known as role allocation. Sec-
ondly, the buyer robot should choose a task to bid for,
then the seller robot will assign the tasks to each buyer
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
104

reasonably, this step is known as task allocation. An
iterative greedy method is applied in our implementa-
tion for the step of task allocation.
For the coordinated decision making in decen-
tralized multi-robot system, robots should make their
plans according to the local observable information
with limited communication. This paper takes the
problem of multi-robot search and rescue in danger-
ous environments as the background. The conception
of our trade-based approach can meet the system’s
requirements of useability, efficiency and robustness.
The first experiment we have conducted is designed
to evaluate the performance of our proposed method,
and the second is designed to test the robustness (in
the case of information loss). The experimental re-
sults demonstrate that, our trade-based approach has
a good efficiency for decentralized multi-robot explo-
ration.
However, the actual limitation of the proposed ap-
proach is that it can not guarantee the global optimal
solution will be found, i.e. the task allocation plan for
the whole mission is sometimes not optimal. Future
work will improve the step of task allocation. An im-
plementable idea is that the buyer robot can send the
purchase request to the seller robot for several tasks,
then seller robot will evaluate the purchase requisi-
tions and assign the tasks with a more advanced algo-
rithm (i.e. improve Algorithm 2).
REFERENCES
Burgard, W., Moors, M., Fox, D., Simmons, R., and Thrun,
S. (2000). Collaborative multi-robot exploration. In
Proceedings of the 2000 IEEE International Confer-
ence on Robotics and Automation (ICRA’00), pages
476–481, San Francisco, CA, USA.
Cao, Y. U., Fukunaga, A. S., and Kahng, A. (1997). Coop-
erative mobile robotics: Antecedents and directions.
Autonomous Robots, 4(1):7–27.
Dudek, G., Jenkin, M. R. M., Milios, E., and Wilkes, D.
(1996). A taxonomy for multi-agent robotics. Au-
tonomous Robots, 3(4):375–397.
Gerkey, B. P. and Matari´c, M. J. (2002). Sold!: Auction
methods for multirobot coordination. IEEE Transac-
tions on Robotics and Automation, 18(5):758–768.
Gerkey, B. P. and Matari´c, M. J. (2004). A formal analysis
and taxonomy of task allocation in multi-robot sys-
tems. The International Journal of Robotics Research,
23(9):939–954.
Gerkey, B. P., Vaughan, R. T., and Howard, A. (2003).
The player/stage project: Tools for multi-robot and
distributed sensor systems. In Proceedings of the
11th International Conference on Advanced Robotics
(ICAR’03), pages 317–323, Coimbra, Portugal.
Ko, J., Stewart, B., Fox, D., Konolige, K., and Limketkai,
B. (2003). A practical, decision-theoretic approach
to multi-robot mapping and exploration. In Proceed-
ings of the 2003 IEEE/RSJ International Conference
on Intelligent Robots and Systems (IROS’03), pages
3232–3238, Las Vegas, NV, USA.
Kuhn, H. W. (1955). The hungarian method for the assign-
ment problem. Naval Research Logistics Quarterly,
2(1):83–97.
LaValle, S. M. (2006). Planning Algorithms. Cambridge
University Press.
Marjovi, A., Nunes, J. G., Marques, L., and de Almeida, A.
(2009). Multi-robot exploration and fire searching. In
Proceedings of the 2009 IEEE/RSJ International Con-
ference on Intelligent Robots and Systems (IROS’09),
pages 1929–1934, St. Louis, MO, USA.
Rekleitis, I. M., Dudek, G., and Milios, E. E. (2000). Multi-
robot collaboration for robust exploration. In Pro-
ceedings of the 2000 IEEE International Conference
on Robotics and Automation (ICRA’00), pages 3164–
3169, San Francisco, CA, USA.
Stachniss, C., Mozos,
´
O. M., and Burgard, W. (2009). Ef-
ficient exploration of unknown indoor environments
using a team of mobile robots. Annals of Mathematics
and Artificial Intelligence, 52(2):205ff.
Thrun, S. (1998). Learning metric-topological maps for in-
door mobile robot navigation. Artificial Intelligence,
99(1):21–71.
Ulrich, I. and Borenstein, J. (1998). VFH+: Reliable obsta-
cle avoidance for fast mobile robots. In Proceedings of
the 1998 IEEE International Conference on Robotics
and Automation (ICRA’98), pages 1572–1577, Leu-
ven, Belgium.
Wurm, K. M., Stachniss, C., and Burgard, W. (2008).
Coordinated multi-robot exploration using a segmen-
tation of the environment. In Proceedings of the
2008 IEEE/RSJ International Conference on Intel-
ligent Robots and Systems (IROS’08), pages 1160–
1165, Nice, France.
Yamauchi, B. (1998). Frontier-based exploration using mul-
tiple robots. In Proceedings of the 2nd International
Conference on Autonomous Agents (Agents’98), pages
47–53, Minneapolis, MN, USA.
Yan, Z., Jouandeau, N., and Ali Cherif, A. (2010).
Sampling-based multi-robot exploration. In Proceed-
ings of the Joint 41th International Symposium on
Robotics and 6th German Conference on Robotics
(ISR/ROBOTIK 2010), pages 44–49, Munich, Ger-
many.
Zlot, R., Stentz, A. T., Dias, M. B., and Thayer, S. (2002).
Multi-robot exploration controlled by a market econ-
omy. In Proceedings of the 2002 IEEE International
Conference on Robotics and Automation (ICRA’02),
pages 3016–2023, Washington, DC, USA.
MULTI-ROBOT DECENTRALIZED EXPLORATION USING A TRADE-BASED APPROACH
105
