A PARALLEL ONLINE REGULARIZED LEAST-SQUARES
MACHINE LEARNING ALGORITHM FOR FUTURE
MULTI-CORE PROCESSORS
Tapio Pahikkala, Antti Airola, Thomas Canhao Xu, Pasi Liljeberg
Hannu Tenhunen and Tapio Salakoski
Turku Centre for Computer Science (TUCS) and Department of Information Technology
University of Turku, Joukahaisenkatu, Turku, Finland
Keywords:
Machine learning, Network-on-Chip, Online learning, Regularized least-squares.
Abstract:
In this paper we introduce a machine learning system based on parallel online regularized least-squares learn-
ing algorithm implemented on a network on chip (NoC) hardware architecture. The system is specifically
suitable for use in real-time adaptive systems due to the following properties it fulfills. Firstly, the system is
able to learn in online fashion, a property required in almost all real-life applications of embedded machine
learning systems. Secondly, in order to guarantee real-time response in embedded multi-core computer archi-
tectures, the learning system is parallelized and able to operate with a limited amount of computational and
memory resources. Thirdly, the system can learn to predict several labels simultaneously which is beneficial,
for example, in multi-class and multi-label classification as well as in more general forms of multi-task learn-
ing. We evaluate the performance of our algorithm from 1 thread to 4 threads, in a quad-core platform. A
Network-on-Chip platform is chosen to implement the algorithm in 16 threads. The NoC consists of a 4x4
mesh. Results show that the system is able to learn with minimal computational requirements, and that the
parallelization of the learning process considerably reduces the required processing time.
1 INTRODUCTION
The design of adaptive systems is an emerging topic
in the area of pervasive and embedded computing.
Rather than exhibiting pre-programmed behavior, it
would in many applications be beneficial for systems
to be able to adapt to their environment. Imagine
smart music players that adapt to the musical prefer-
ences of their owner, intelligent traffic systems that
monitor and predict traffic conditions and re-direct
cars accordingly, etc. Clearly, it would be useful in
such applications, if the considered system could au-
tomatically learn to perform the desired task, and over
time improve its performance as more feedback is
gained.
1.1 Machine Learning in Embedded
Systems
Machine learning (ML) is a branch of computer sci-
ence founded on the idea of designing computer al-
gorithms capable of improving their prediction per-
formance automatically over time through experience
(Mitchell, 1997). Such approaches offer the possibil-
ity to gain new knowledge through automated discov-
ery of patterns and relations in data. Further, these
methods can provide the benefit of freeing humans
from doing laborious and repetitive tasks, when a
computer can be trained to perform them. This is es-
pecially important in problem areas where there are
massive amounts of complex data available, such as
in image recognition or natural language processing.
In the recent years ML methods have increasingly
been applied in non-traditional computing platforms,
bringing both new challenges and opportunities. The
shift from the single processor paradigm to paral-
lel computing systems such as multi-core processors,
cloud computing environments, graphic processing
units (GPUs) and the network on chip (NoC) has re-
sulted in a need for parallelizable learning methods
(Chu et al., 2007; Zinkevich et al., 2009; Low et al.,
2010).
At the same time, the widespread use of embed-
ded systems ranging from industrial process control
systems to wearable sensors and smart-phones have
opened up new application areas for intelligent sys-
590
Pahikkala T., Airola A., Canhao Xu T., Liljeberg P., Tenhunen H. and Salakoski T..
A PARALLEL ONLINE REGULARIZED LEAST-SQUARES MACHINE LEARNING ALGORITHM FOR FUTURE MULTI-CORE PROCESSORS.
DOI: 10.5220/0003411405900599
In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems (SAAES-2011), pages
590-599
ISBN: 978-989-8425-48-5
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

tems. Some such recent ML applications include
embedded real-time vision systems for field pro-
grammable gate arrays(Farabet et al., 2009), person-
alized health applications for mobile phones (Oresko
et al., 2010) and sensor based video-game controls
that learn to recognize user movements (Bogdanow-
icz, 2011). For a thorough review of the design re-
quirements of machine learning methods in embed-
ded systems we refer to (Swere, 2008).
Majority of present-day machine learning re-
search focuses on so-called batch learning methods.
Such methods, given a data set for training, run a
learning process on the data set and then output a
predictor which remains fixed after the initial train-
ing has been finished. In contrast, it would be ben-
eficial in real-time embedded systems for learning to
be an ongoing process in which the predictors would
be upgraded whenever new data become available. In
machine learning literature, this type of methods are
often referred to as online learning algorithms (Bot-
tou and Le Cun, 2004). One of the principal areas of
application of this type of adaptive learning systems
are hand-held devices such as smart-phones that learn
to adapt to their users preferences.
In this work we consider how to implement in par-
allel online learning methods for (multi-class) clas-
sification in embedded computing environments. In
classification, the system must assign a class label to a
new object given the feature representation of the ob-
ject. For example, in spam classification the features
could be the words in an e-mail message, and possi-
ble classes consist of {spam, not-spam}, whereas in
optical character recognition features could represent
image scans and the set of available classes would en-
code different characters in the alphabet.
Our method is built upon the regularized least-
squares (RLS) (Rifkin et al., 2003; Poggio and Smale,
2003), also known as the least-squares support vector
machine (Suykens et al., 2002) and ridge regression
(Hoerl and Kennard, 1970), which is is a state-of-
the art machine learning method suitable both for re-
gression and classification. Compared to the ordinary
least-squares method introduced by Gauss, RLS is
known to often achieve better predictive performance,
as the regularization allows one to avoid over-fitting
to the training data. An important property of the al-
gorithm is that it has a closed form solution, which
can be fully expressed in terms of matrix operations.
This allows developing efficient computational short-
cuts for the method, since small changes in the train-
ing data matrix correspond to low-rank changes in the
learned predictor.
An online version of the ordinary (non-
regularized) least-squares method was presented
more than half a century ago by (Plackett, 1950). The
method has since then been widely used in real-time
applications in areas such as machine learning, signal
processing, communications and control systems.
Online learning with RLS is also known in the
machine learning literature (see e.g. (Zhdanov and
Kalnishkan, 2010) and references therein). In this
work we extend online RLS for multi-output learning
and present an implementation that takes advantage
of parallel computing architectures. Thus, the
method allows adaptive learning efficiently in parallel
environments, and is applicable to a wide range of
problems both for regression and classification, and
for single and multi-task learning.
1.2 Future Multi-core Systems
Many embedded systems suffer from limited pro-
cessing ability as they usually have only one rela-
tively slow system-on-chip (SoC) processors. Since
the beginning of the 21st century, Network-on-Chip
(NoC) has become an emerging and promising solu-
tion in the Chip Multiprocessor (CMP) field (Dally
and Towles, 2001). This is due to the fact that the
traditional design methods such as SoC have encoun-
tered critical challenges and bottlenecks as the num-
ber of on-chip integrated components increases. One
of the most well known and critical problems is the
communication bottleneck. Most traditional SoCs
have the bus based communication architecture, such
as simple, hierarchical or crossbar-type buses. In con-
trast with the increasing chip capacity, bus based sys-
tems do not scale well with the system size in terms of
bandwidth, clock frequency and power consumption
(Dally and Towles, 2001).
To address these problems and improve the sys-
tem performance, NoC is proposed and endeavors to
bring network communication methodologies to the
on-chip communication. The NoC design approach
is to create a communication interconnect beforehand
and then map the computational resources to it via re-
source dependent interfaces. Figure 1 shows a 4×4
mesh based NoC topology. The underlying network
is comprised of network links and routers (R), each of
which is connected to a processing element (PE) via
a network interface (NI). The basic architectural unit
of a NoC is the tile/node (N) which is consisted of a
router, its attached NI and PE, and the corresponding
links. Communication among PEs is achieved via the
transmission of network packets. Intel
1
has demon-
strated an 80 tile, 100M transistor, 275mm
2
2D NoC
1
Intel is a trademark or registered trademark of Intel or
its subsidiaries. Other names and brands may be claimed as
the property of others.
A PARALLEL ONLINE REGULARIZED LEAST-SQUARES MACHINE LEARNING ALGORITHM FOR FUTURE
MULTI-CORE PROCESSORS
591

under 65nm technology (Vangal et al., 2007). An ex-
perimental microprocessor containing 48 x86 cores
on a chip has been created using 4×6 2D mesh topol-
ogy with 2 cores per tile (Intel, 2010). Therefore, in
this paper, NoC is chosen to be the platform for the
study of the online machine learning algorithm.
PE
NI
R
S
N
W
E
Figure 1: An example of 4×4 NoC using mesh topology.
1.3 Contributions of the Paper
In this work we introduce the parallel online RLS
method, and explore its suitability for implementing
adaptive systems on the NoC platform. The proposed
approach has the following key benefits:
• The system can automatically learn to perform a
task given examples of desired behavior, and can
incorporate information from new training exam-
ples in an online fashion. This process may go on
indefinitely, meaning lifelong learning.
• The system learns to predict several labels si-
multaneously which is beneficial, for example, in
multi-class and multi-label classification as well
as in more general forms of multi-task learning.
• Learning is parallelized and requires minimal
storage and computational resources.
• The system is shown to work well on both on a
quad-core platform and a NoC platform with 16
threads.
We expect that methods such as the online RLS have
the capability to serve as the enabling technology for a
wide range of applications in adaptive embedded sys-
tems.
2 ALGORITHM DESCRIPTIONS
2.1 Regularized Least-Squares
We start by introducing some notation. Let R
m
and
R
m×n
, where m,n ∈ N, denote the sets of real valued
column vectors and m × n-matrices, respectively. To
denote real valued matrices and vectors we use bold
capital letters and bold lower case letters, respectively.
Moreover, index sets are denoted with calligraphic
capital letters. By denoting M
i
, M
:, j
, and M
i, j
, we
refer to the ith row, jth column, and i, jth entry of the
matrix M ∈ R
m×n
, respectively. Similarly, for index
sets R ⊆ {1,...,n} and L ⊆ {1,...,m}, we denote
the submatrices of M having their rows indexed by R ,
the columns by L, and the rows by R and columns by
L as M
R
, M
:,L
, and M
R ,L
, respectively. We use an
analogous notation also for column vectors, that is, v
i
refers to the ith entry of the vector v.
Let X ∈ R
m×n
be a matrix containing the fea-
ture representation of the examples in the training set,
where n is the number of features and m is the num-
ber of training examples. The i, jth entry of X con-
tains the value of the jth feature in the ith training
example. Moreover, let Y ∈ R
m×l
be a matrix con-
taining the labels of the training examples. We as-
sume each data point to have altogether l labels and
the i, jth entry of Y contains the value of the jth label
of the ith training example. In multi-class or multi-
label classification, the labels can be restricted to be
either 1 or −1 depending whether the data points be-
longs to the class, for example, while they can be any
real numbers in multi-label regression tasks (see e.g.
(Hsu et al., 2009) and references therein).
As an example, consider that we have a set of m
images, each of which is represented by n features.
In addition, each image is associated with an array of
l binary labels of which the value of the jth label is
1 if the object indexed by j is depicted in the image
and −1 otherwise. Our aim is to learn from the set of
images to predict what is depicted in a any new image
unseen in the set.
In this paper, we consider linear predictors of type
f (x) = W
T
x, (1)
where W ∈ R
n×l
is the matrix representation of the
learned predictor and x ∈ R
n
is a data point for which
the prediction of l labels is to be made.
2
The computa-
tional complexity of making predictions with (1) and
the space complexity of the predictor are both O(nl)
provided that the feature vector representation x for
the new data point is given.
Given training data X,Y, we find W by minimiz-
ing the RLS risk. This can be expressed as the follow-
ing problem:
2
In the literature, the formula of the linear predictors of-
ten also contain a bias term. Here, we assume that if such
a bias is used, it will be realized by using an extra constant
valued feature in the data points.
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
592

argmin
W∈R
n×l

kXW − Yk
2
F
+ λkWk
2
F

, (2)
where k · k
F
denotes the Frobenius norm which is de-
fined for a matrix M ∈ R
n×l
as
kMk
F
=
v
u
u
t
n
∑
i=1
l
∑
j=1
(M
i, j
)
2
.
The first term in (2), called the empirical risk, mea-
sures how well the prediction function fits to the train-
ing data. The second term is called the regularizer and
it controls the tradeoff between the empirical error on
the training set and the complexity of the prediction
function.
2.2 Batch Learning for RLS
A straightforward approach to solve (2) is to set the
derivative of the objective function with respect to W
to zero. Then, by solving it with respect to W, we get
W = (X
T
X + λI)
−1
X
T
Y, (3)
where I is the identity matrix. We note (see e.g. (Hen-
derson and Searle, 1981)) that an equivalent result can
be obtained from
W = X
T
(XX
T
+ λI)
−1
Y. (4)
If the number of features n is smaller than the number
of training examples m, it is computationally benefi-
cial to use the form (3) while using (4) is faster in the
opposite case. Namely, the computational complexity
of (3) is O(n
3
+n
2
m+nml), where the first term is the
complexity of the matrix inversion, the second comes
from multiplying X
T
with X, and the third from mul-
tiplying the result of the inversion with the matrix Y.
The complexity of (4) is O(m
3
+ m
2
n + nml), where
the terms are analogous to those of (3). Putting these
two together, the complexity of training a predictor
is O(nm(min{n,m} + l)). It is also straightforward
to see from (3) and (4) that the space complexity
O(m(n + l)) of RLS directly depends on the size of
the matrices X and Y.
One of the benefits of RLS is that the number of
labels per data point l can be increased up to the level
of m or n until it starts to have an effect on the space
and time complexities of RLS training. That is, we
can solve several prediction tasks almost at the cost
of solving only one. This is beneficial especially in
multi-class and multi-label classification tasks, for ex-
ample.
2.3 Online Learning for RLS
Next, we consider a computational short-cut for up-
dating a learned RLS predictor when a new training
example arrives. The short-cut is then used to con-
struct an online version of the RLS algorithm. Simi-
lar considerations have already been presented in the
machine learning literature ( see e.g. (Zhdanov and
Kalnishkan, 2010) and references therein) but here we
formalize it for the first time for multiple outputs, that
is, for the case in which the data points can have more
than one label.
First, we present the following well-known re-
sult which is often referred to as the matrix inversion
lemma or the Sherman-Morrison-Woodbury formula
(see e.g. (Horn and Johnson, 1985, p. 18)):
Lemma 2.1. Let M ∈ R
a×a
, N ∈ R
b×b
, P ∈ R
a×b
,
and Q ∈ R
b×a
be matrices. If M, N, and M − PNQ
are invertible, then
(M − PNQ)
−1
= M
−1
− M
−1
P(N
−1
− QM
−1
P)
−1
QM
−1
.
(5)
The main consequence of this result is that if we al-
ready know the inverse of the matrix M and if b << a,
we can save a considerable amount of computational
resources by using the right hand side of (5) instead
of computing an inverse of an a × a matrix.
Assume that we have already trained an RLS pre-
dictor from the training set X ∈ R
m×n
,Y ∈ R
m×l
with
a regularization parameter value λ, and hence we have
W stored in memory. In addition, let us assume that
during the training process, we have computed the
matrix
C = (X
T
X + λI)
−1
and stored it in memory. According to (3), we have
W = CX
T
Y. Moreover, let x ∈ R
n
,y ∈ R
l
be a
new data point unseen in the training set and let
b
X ∈ R
(m+1)×n
,
b
Y ∈ R
(m+1)×l
be the new training set
including the new training example. Now, since we
already have the matrix C stored in memory, we can
use the matrix inversion lemma to speed up the com-
putation of the matrix
b
C corresponding to the updated
training set:
b
C = (X
T
X + xx
T
+ λI)
−1
(6)
= (C
−1
+ xx
T
)
−1
= (C − Cx(x
T
Cx + 1)
−1
x
T
C), (7)
where the calculation of (7) requires only O(n
2
) time
instead of the O(n
3
) time required in (6). The predic-
tor
c
W corresponding to the updated training set can
then be computed from
c
W =
b
C(X
T
Y + xy
T
) (8)
in O(ln
2
) time provided that X
T
Y has already been
computed during training with the original training
set. If there are altogether m training examples, which
A PARALLEL ONLINE REGULARIZED LEAST-SQUARES MACHINE LEARNING ALGORITHM FOR FUTURE
MULTI-CORE PROCESSORS
593

are added into the training set one at a time, the over-
all computational complexity of this online variation
would be O(mln
2
), which is slower than the batch
RLS training if the number of labels per training ex-
amples l is large.
Next, we show how to improve the complexity
even further. Let us first define some extra notation.
Let
v = Cx, (9)
c = x
T
v,
d = (c + 1)
−1
, and
p = W
T
x. (10)
Continuing from (7) and (8), we get
c
W = (C − Cx(x
T
Cx + 1)
−1
x
T
C)(X
T
Y + xy
T
)
= (C − dvv
T
)(X
T
Y + xy
T
) (11)
= CX
T
Y + Cxy
T
− dvv
T
X
T
Y − dvv
T
xy
T
= W + vy
T
− dvp
T
− cdvy
T
= W + v((1 − cd)y
T
− dp
T
). (12)
The computational complexity of calculating
c
W from
(12) requires O(n
2
+ nl) time. Here, the first term is
the complexity of calculating
b
C with (7) and v with
(9). The second term is the complexity of calculat-
ing p with (10), multiplying v with (1 − cd)y
T
− dp
T
,
and adding the result to W in (12). Multiplying the
complexity of a single iteration with the number of
training examples m, we get the overall training time
complexity of online RLS O(mn
2
+ mnl). Thus, on-
line training of RLS with a set of m data points is
computationally as efficient as the training of batch
RLS with (3) and provides exactly equivalent results.
Batch learning with (4) is more efficient only if m < n
but this is rarely the case in the lifelong learning set-
ting considered in this paper. The space complexity
of online RLS is O(n
2
+ nl), where the first term is
the cost of keeping the matrix C in memory and the
second is that of the matrix W.
Putting everything together, we present the online
RLS in Algorithm 1. The algorithm first starts from an
empty training set (lines 1-2). Next, it read a feature
representation of a new data point (line 4) and outputs
a vector of predicted labels for the data point (line 5).
After the prediction, the method is given a feedback in
the form of the correct label vector of the data point
(line 6). Finally, the features and labels of the new
data point are used to update the predictor (lines 7-
11). The steps 4-11 are reiterated whenever new data
are observed.
Algorithm 1: Pseudo code for Online RLS.
1: C ← λ
−1
I
2: W ← 0 ∈ R
n
3: for t ∈ 1,2,... do
4: Read data point x
5: Output prediction p ← W
T
x
6: Read true labels y
7: v ← Cx
8: c ← x
T
v
9: d ← (c + 1)
−1
10: C ← C − dvv
T
11: W ← W + v((1 − cd)y
T
− dp
T
)
2.4 Parallelized Online RLS
Because of the layout of matrices in memory and the
nature of the basic matrix operations, it is often pos-
sible to gain considerable performance improvements
with parallelization. Indeed, the parallelization of the
batch RLS has been tested on graphics processing
units by (Do et al., 2008) who reported large gains in
running speed. Here, we consider the parallelization
of online RLS with multiple outputs.
Algorithm 2: Parallel computation for v ← Cx.
1: Split the index set {1,.. .,n} into p disjoint subsets
I
1
,.. .,I
p
of which each of the p processors get one.
2: for h ∈ {1,. .., p} do
3: Load x, v
I
h
, and C
I
h
into cache/memory.
4: for i ∈ I
p
do
5: v
i
← 0
6: for j ∈ {1, ... ,n} do
7: v
i
← v
i
+ C
i, j
x
j
8: return v
Algorithm 3: Parallel computation for C ← C − dvv
T
.
1: Split the index set {1,.. .,n} into p disjoint subsets
I
1
,.. .,I
p
of which each of the p processors get one.
2: for h ∈ {1,. .., p} do
3: Load d, v, and C
I
h
into cache/memory.
4: for i ∈ I
p
do
5: g ← dv
i
6: for j ∈ {1, ... ,n} do
7: C
i, j
← C
i, j
− gv
j
8: return C
The two most expensive parts in Algorithm 1 are
the lines 7 and 10 which both require O(n
2
) time,
and hence we concentrate primarily on those when
designing a parallel version of online RLS. The par-
allelization of the lines 7 and 10 are presented in Al-
gorithms 2 and 3, respectively. In both algorithms,
the outer loop corresponds to distributing the work
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
594

among p processors. The former algorithm is sim-
ply a parallelization of a matrix-vector product which
is widely known in literature but we present if here for
self-sufficiency. The parallelization of the outer prod-
uct of two vectors considered in the latter algorithm
is almost as straightforward. In both cases, there is no
time wasted waiting for memory write locks, because
every processor is updating different memory loca-
tions determined by the index sets. Moreover, if the
processors have a sufficient amount of cache memory
available, the progress can be accelerated even fur-
ther, since the different processors require different
portions of the matrix C.
Finally, we note that if the number of label per
data point l is large, the lines 5 and 11 in Algorithm 1
can be parallelized in similar way as the lines 7 and
10, respectively. This is, because the former contains
a product of a matrix and a vector, and the latter con-
tains an outer product of two vectors. Putting every-
thing together, the computational complexity of a sin-
gle iteration of parallel online RLS is O(n
2
/p+nl/p),
where p is the number of processors. The complex-
ity of learning from a sequence of m data points is m
times the complexity of a single iteration.
3 EXPERIMENTS
We implement the online RLS method in the C++
programming language, and parallelize it via the
OpenMP parallel programming platform. Experi-
ments are run both in a desktop environment with a
multi-core Intel processor, as well as on a NoC simu-
lation platform.
3.1 Recognition of Hand-Written Digits
In the experiments we explore the behavior of the
parallel online RLS on the MNIST handwritten digit
database
3
benchmark. The database consists of 28 ×
28 pixel black and white image scans of handwritten
digits. The features of each image consist of pixel in-
tensity values normalized to {0,1} range. The task is
to be able to predict given the pixel intensity values
of an image, which of the digits from range {0. . . 9}
it represents. We follow the original training-test split
defined in the dataset, which ensures that the test char-
acters have been written by different authors than the
training ones. The training set consists of 60000 ex-
amples, and the test set of 10000 examples. The pixel
intensity values are directly used as the features for
the linear model. We note that developing a state-
of-the art handwritten digit recognition system would
3
Available at http://yann.lecun.com/exdb/mnist/
require more advanced feature engineering and non-
linear modeling but constructing such a system goes
outside the scope of this paper. The regularization pa-
rameter is set to 1 in the experiments.
3.2 Runtime and Classification
Performance
First, we measure the effect of the parallelization on
the runtime required for updating the OnlineRLS pre-
dictor with a new example. We first load the data set
into the memory, and then compute the average time
spent on update over the 60000 training examples.
The experiment is run on an Intel Core i7-950 pro-
cessor machine. The run-times are presented in Fig-
ure 2. On 4 cores the update operations are approx-
imately 3 times faster than on a single core, demon-
strating that substantial speedups can be gained in par-
allel hardware architectures for the method. The CPU
time spent updating the predictor ranges from around
900 to below 300 microseconds per example, depend-
ing on the number of cores, which suggests that the
method could be useful in systems, where only mini-
mal computational times can be afforded.
In Figure 3 we plot the classification performance
of the learned classifier as a function of number of
training examples processed. The prediction perfor-
mance is especially in the early phases of learning
affected by the order in which the training examples
are supplied. Therefore, we compute the average re-
sults over 10 repetitions of the experiment, where at
the start of each experiment the order of the training
examples is shuffled. The error rate measures the rel-
ative fraction of misclassified test examples. Since
all classes are are roughly equally represented in the
test set, naive approaches such as predicting always
the same class, or choosing the class randomly would
lead to around 90% test error. The online RLS method
also begins with predictive performance in this range,
but as more examples are processed, we see signif-
icant improvements, with error rate reaching 14.7%
once all the 60000 training examples have been pro-
cessed. The curve demonstrates the ability of online
RLS to improve its performance by adapting to exam-
ples provided over time.
3.3 NoC Simulation Environment
To evaluate our algorithm further, we use a cycle-
accurate NoC simulator (see Figure 1). The simula-
tion platform is able to produce detailed evaluation
results. The platform models the routers and links ac-
curately. The state-of-the-art router in our platform
includes a routing computation unit, a virtual chan-
A PARALLEL ONLINE REGULARIZED LEAST-SQUARES MACHINE LEARNING ALGORITHM FOR FUTURE
MULTI-CORE PROCESSORS
595

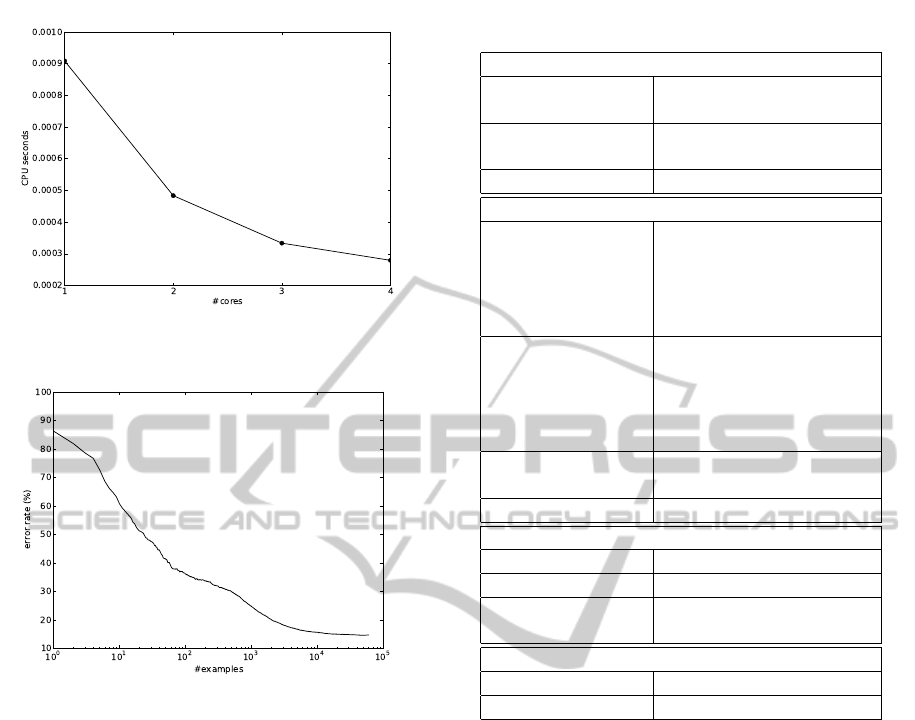
Figure 2: Average computational cost of updating the pre-
dictor with new training example on Mnist.
Figure 3: Error rate on the Mnist data as a function of train-
ing examples.
nel allocator, a switch allocator, a crossbar switch and
four input buffers. Routers in our NoC model have
five ports (North, East, West, South and Local PE) and
the corresponding virtual channels, buffers and cross-
bars. It is noteworthy that not all routers in a NoC
require five ports, e.g. router of N1 in Figure 1 has
only East, South and Local PE ports. Adaptive rout-
ing is used widely in off-chip networks, however de-
terministic routing is favorable for on-chip networks
because the implementation is easier. In this paper,
a dimensional ordered routing (DOR) (Sullivan and
Bashkow, 1977) based X-Y deterministic routing al-
gorithm is selected, in which a message packet (flit)
is first routed to the X direction and last to the Y di-
rection.
We use a 16-node network which models a single-
chip CMP for our experiments. A full system simu-
lation environment with 16 processors has been im-
plemented. The simulations are run on the Solaris 9
operating system based on SPARC instruction set in-
order issue structure. Each processor is attached to
a wormhole router and has a private write-back L1
Table 1: System configuration parameters.
Processor configuration
Instruction set
architecture
SPARC
Number of pro-
cessors
16
Issue width 1
Cache configuration
L1 cache Private, split instruction
and data cache, each
cache is 16KB. 4-way as-
sociative, 64-bit line, 3-
cycle access time
L2 cache Shared, distributed in 4
layers, unified 2-16MB
(16 banks, each 256KB-
1MB). 64-bit line, 6-
cycle access time
Cache coherence
protocol
MESI
Cache hierarchy SNUCA
Memory configuration
Size 4GB DRAM
Access latency 260 cycles
Requests per
processor
16 outstanding
Network configuration
Router scheme Wormhole
Flit size 128 bits
cache. The L2 cache shared by all processors is split
into banks. The size of each cache bank node is 1MB;
hence the total size of shared L2 cache is 16MB. Each
L2 cache bank is attached to a router as well. The sim-
ulated memory/cache architecture mimics SNUCA
(Kim et al., 2002). A two-level distributed direc-
tory cache coherence protocol called MESI (Patel and
Ghose, 2008) has been used in our memory hierar-
chy in which each L2 bank has its own directory.
Four types of cache line status, namely Modified (M),
Exclusive (E), Shared (S) and Invalid (I) are imple-
mented. We use Simics (Magnusson et al., 2002) full
system simulator as our simulation platform. The de-
tailed configurations of processor, cache and memory
configurations can be found in Table 1.
3.4 NoC Simulation Result Analysis
The normalized full system simulation results are
shown in Figures 4 and 5. We use the machine learn-
ing algorithm with 16 threads. The problem size for
our simulation is 100 inputs. To analyze the tempo-
ral locality of our algorithm, we estimate the cache
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
596

0
0.5
1
1.5
2
2.5
3
0 2000 4000 6000 8000 10000 12000 14000 16000
Miss Rate (%)
Cache Size (KB)
Our Algorithm
Figure 4: Cache miss rate versus cache size.
90
92
94
96
98
100
2,048 4,096 8,192
16,384
Normalized Average Network Latency
Cache Size (KB)
Figure 5: Normalized average network latency with differ-
ent number of pillars.
miss rate with different L2 cache sizes. For shared
memory CMPs, a large last level cache is crucial, be-
cause a miss in the cache will require an access to
the off-chip main memory. Figure 4 show that, as
the cache size increases, the cache miss rate decreases
gradually (From 2.79% to 1.48%). The main reason is
that, in our algorithm, the data-set is pre-loaded into
the cache-memory first. More data-set and interme-
diate data can be stored with a larger cache. Aver-
age network latency represents the average number
of cycles required for the transmission of all network
messages. For each message, the number of cycle is
calculated as, from the injection of a message header
into the network at the source node, to the reception
of a tail flit at the destination node. As illustrated in
Figure 5, the 16MB configuration outperforms oth-
ers in terms of average network latency. The latency
in 16MB configuration is 1.73%, 3.53% and 4.56%
lower than the 8MB, 4MB and 2MB configurations,
respectively. This is primarily due to the reduced
cache miss rate in the 16MB configuration compared
to the other configurations. We notice that, an off-
chip access of the main memory will result a signifi-
cant higher network latency. However, since there are
millions of cache/memory accesses, the impact is less
significant as a whole.
4 DISCUSSION AND FUTURE
WORK
The most immediate bottleneck in the considered par-
allel online RLS algorithm is its quadratic scaling
with respect to n, the number of features in the data
points, because both the space and time complexi-
ties are quadratic in n. Therefore, combining the
algorithm with feature selection techniques (see e.g.
(Guyon and Elisseeff, 2003)) when the classification
tasks involve high dimensional data can be a fruitful
research direction. A suitable technique for this pur-
pose would be, for example, the computationally effi-
cient feature selection algorithm for RLS proposed by
us in (Pahikkala et al., 2010). In the future, we plan
to develop algorithms which would perform online
learning and feature selection simultaneously. There
is already some prior work on this type of algorithms
(see e.g. (Jung and Polani, 2006)).
5 CONCLUSIONS
We have introduced a machine learning system which
is based on parallel online regularized least-squares
learning algorithm and implemented on a network on
chip (NoC) platform. The system is specifically suit-
able for use in real-time adaptive systems due to the
following properties it fulfills:
• The system is able to learn in online fashion, that
is, it can update itself in real-time whenever new
data is observed. This is an essential property in
real-life applications of embedded machine learn-
ing systems, for example, in smart-phone applica-
tions that aim to adapt to their owners preferences.
• The learning system is parallelized and works
with limited processor time and memory. This
opens the possibilities to deploy the system, for
example, into small hand-held devices which op-
erate in real-time.
• The system can carry out complex learning tasks
involving simultaneous prediction of several la-
bels per data point. Typical examples of this type
of tasks are, for example, in multi-class and multi-
label classification.
The run-time performance of the proposed system
was evaluated using 1 to 4 threads, in a quad-core
platform. It was shown that, as expected according to
A PARALLEL ONLINE REGULARIZED LEAST-SQUARES MACHINE LEARNING ALGORITHM FOR FUTURE
MULTI-CORE PROCESSORS
597

the theoretical considerations, the performance gain
is roughly linear with respect to the number of cores.
In an additional experiment, we used NoC platform
to test the system in 16 threads. The NoC consists
of a 4x4 mesh. The obtained results demonstrated
that the system is able to learn with minimal com-
putational requirements, and that the parallelization
of the learning process considerably reduces the re-
quired processing time.
Altogether, the study sheds light on the possibili-
ties of deploying modern machine learning methods
into embedded systems based on future multi-core
computing architectures. For example, the machine
learning techniques that are able to operate in real
time and in online fashion are promising tools for pur-
suing adaptivity of embedded systems. This is be-
cause they enable the real time updating of the system
according to the data observed from the environment.
While we used a digit recognition task as case study
in this paper, the learning system can be applied on a
wide range of other tasks such as energy efficiency or
control of the embedded systems.
ACKNOWLEDGEMENTS
This work has been supported by the Academy of Fin-
land.
REFERENCES
Bogdanowicz, A. (2011). The motion tech behind Kinect.
IEEE The Institute. Published Online 6. January 2011
http://www.theinstitute.ieee.org.
Bottou, L. and Le Cun, Y. (2004). Large scale online learn-
ing. In Thrun, S., Saul, L., and Sch
¨
olkopf, B., editors,
Advances in Neural Information Processing Systems
16. MIT Press, Cambridge, MA.
Chu, C.-T., Kim, S. K., Lin, Y.-A., Yu, Y., Bradski, G., Ng,
A. Y., and Olukotun, K. (2007). Map-reduce for ma-
chine learning on multicore. In Sch
¨
olkopf, B., Platt,
J., and Hoffman, T., editors, Advances in Neural Infor-
mation Processing Systems 19, pages 281–288. MIT
Press, Cambridge, MA.
Dally, W. J. and Towles, B. (2001). Route packets, not
wires: on-chip inteconnection networks. In Proceed-
ings of the 38th conference on Design automation,
pages 684–689.
Do, T.-N., Nguyen, V.-H., and Poulet, F. (2008). Speed up
SVM algorithm for massive classification tasks. In
Tang, C., Ling, C. X., Zhou, X., Cercone, N., and
Li, X., editors, Proceedings of the 4th International
Conference on Advanced Data Mining and Applica-
tions (ADMA 2008), volume 5139 of Lecture Notes in
Computer Science, pages 147–157. Springer.
Farabet, C., Poulet, C., and LeCun, Y. (2009). An fpga-
based stream processor for embedded real-time vision
with convolutional networks. In Fifth IEEE Workshop
on Embedded Computer Vision (ECV’09), pages 878–
885. IEEE.
Guyon, I. and Elisseeff, A. (2003). An introduction to vari-
able and feature selection. Journal of Machine Learn-
ing Research, 3:1157–1182.
Henderson, H. V. and Searle, S. R. (1981). On deriving the
inverse of a sum of matrices. SIAM Review, 23(1):53–
60.
Hoerl, A. E. and Kennard, R. W. (1970). Ridge regression:
Biased estimation for nonorthogonal problems. Tech-
nometrics, 12:55–67.
Horn, R. and Johnson, C. R. (1985). Matrix Analysis. Cam-
bridge University Press, Cambridge.
Hsu, D., Kakade, S., Langford, J., and Zhang, T. (2009).
Multi-label prediction via compressed sensing. In
Bengio, Y., Schuurmans, D., Lafferty, J., Williams,
C. K. I., and Culotta, A., editors, Advances in Neural
Information Processing Systems 22, pages 772–780.
MIT Press.
Intel (2010). Single-chip cloud computer. http://
techresearch.intel.com/articles/Tera-Scale/1826.htm.
Jung, T. and Polani, D. (2006). Sequential learning with ls-
svm for large-scale data sets. In Kollias, S. D., Stafy-
lopatis, A., Duch, W., and Oja, E., editors, Proceed-
ings of the 16th International Conference on Artifi-
cial Neural Networks (ICANN 2006), volume 4132 of
Lecture Notes in Computer Science, pages 381–390.
Springer.
Kim, C., Burger, D., and Keckler, S. W. (2002). An adap-
tive, non-uniform cache structure for wire-delay dom-
inated on-chip caches. In ACM SIGPLAN, pages 211–
222.
Low, Y., Gonzalez, J., Kyrola, A., Bickson, D., Guestrin, C.,
and Hellerstein, J. M. (2010). Graphlab: A new frame-
work for parallel machine learning. In The 26th Con-
ference on Uncertainty in Artificial Intelligence (UAI
2010).
Magnusson, P., Christensson, M., Eskilson, J., Forsgren, D.,
Hallberg, G., Hogberg, J., Larsson, F., Moestedt, A.,
and Werner, B. (2002). Simics: A full system simula-
tion platform. Computer, 35(2):50–58.
Mitchell, T. M. (1997). Machine Learning. McGraw-Hill,
New York.
Oresko, J. J., Jin, Z., Cheng, J., Huang, S., Sun, Y.,
Duschl, H., and Cheng, A. C. (2010). A wearable
smartphone-based platform for real-time cardiovascu-
lar disease detection via electrocardiogram process-
ing. IEEE Transactions on Information Technology
in Biomedicine, 14:734–740.
Pahikkala, T., Airola, A., and Salakoski, T. (2010). Speed-
ing up greedy forward selection for regularized least-
squares. In Draghici, S., Khoshgoftaar, T. M., Palade,
V., Pedrycz, W., Wani, M. A., and Zhu, X., editors,
Proceedings of The Ninth International Conference
on Machine Learning and Applications (ICMLA’10),
pages 325–330. IEEE.
PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems
598

Patel, A. and Ghose, K. (2008). Energy-efficient mesi cache
coherence with pro-active snoop filtering for multi-
core microprocessors. In Proceeding of the thirteenth
international symposium on Low power electronics
and design, pages 247–252.
Plackett, R. L. (1950). Some theorems in least squares.
Biometrika, 37(1/2):pp. 149–157.
Poggio, T. and Smale, S. (2003). The mathematics of learn-
ing: Dealing with data. Notices of the American Math-
ematical Society (AMS), 50(5):537–544.
Rifkin, R., Yeo, G., and Poggio, T. (2003). Regularized
least-squares classification. In Suykens, J., Horvath,
G., Basu, S., Micchelli, C., and Vandewalle, J., edi-
tors, Advances in Learning Theory: Methods, Model
and Applications, volume 190 of NATO Science Series
III: Computer and System Sciences, chapter 7, pages
131–154. IOS Press, Amsterdam.
Sullivan, H. and Bashkow, T. R. (1977). A large scale, ho-
mogeneous, fully distributed parallel machine. In Pro-
ceedings of the 4th annual symposium on Computer
architecture, pages 105–117.
Suykens, J., Van Gestel, T., De Brabanter, J., De Moor,
B., and Vandewalle, J. (2002). Least Squares Support
Vector Machines. World Scientific Pub. Co., Singa-
pore.
Swere, E. A. (2008). Machine Learning in Embedded Sys-
tems. PhD thesis, Loughborough University.
Vangal, S., Howard, J., Ruhl, G., Dighe, S., Wilson, H.,
Tschanz, J., Finan, D., Iyer, P., Singh, A., Jacob, T.,
Jain, S., Venkataraman, S., Hoskote, Y., and Borkar,
N. (2007). An 80-tile 1.28tflops network-on-chip in
65nm cmos. In IEEE International Solid-State Cir-
cuits Conference ISSCC 2007, pages 98–589. IEEE.
Zhdanov, F. and Kalnishkan, Y. (2010). An identity for ker-
nel ridge regression. In Hutter, M., Stephan, F., Vovk,
V., and Zeugmann, T., editors, Proceedings of the 21st
international conference on Algorithmic learning the-
ory, volume 6331 of Lecture Notes in Computer Sci-
ence, pages 405–419, Berlin, Heidelberg. Springer-
Verlag.
Zinkevich, M., Smola, A., and Langford, J. (2009). Slow
learners are fast. In Bengio, Y., Schuurmans, D., Laf-
ferty, J., Williams, C. K. I., and Culotta, A., editors,
Advances in Neural Information Processing Systems
22, pages 2331–2339.
A PARALLEL ONLINE REGULARIZED LEAST-SQUARES MACHINE LEARNING ALGORITHM FOR FUTURE
MULTI-CORE PROCESSORS
599