THE MATCHING FOR THE MULTI-PROJECT

COLLABORATIVE PLAN OF NEW PRODUCT DEVELOPMENT

AND RESOURCE BASED ON GENERALIZED RESOURCE UNIT

XiaoGang Deng, Gang Guo

Academic of Machinery Engineering, cqust, Street, Chong qing, China

Gang Guo

College of Mechanical Engineering, Chongqing University, Chong qing, China

Keywords: Generalized resource unit, Multi-project collaborative plan, Plan matching with resource constraint.

Abstract: The Objective is the matching of collaborative development of products in manufacturing enterprises

including involvement of suppliers on a large scale. Match function for collaborative multi-project planning

and design resources is analyzed under different requirements and time intervals, when any conflicts exist.

A generalized design resource unit and a resource granule quantification model are defined. A multi-project

collaborative planning and resource granule constraint-matching model with realization algorithm is

presented. According to plan matching with resource granule, new product development with multi-project

collaborative planning method, based on generalized design resource constraint is proposed. Presented is a

case according to the model and planning which demonstrates the feasibility of the method.

1 INTRODUCTION

In the industry chain cluster, OEMs often need the

simultaneous design and development of several new

products in order to gain the initiative in competition.

This results in a number of project groups that may be

formed between internal organizations and suppliers,

where each project needs to be implemented by

matching the appropriate design resources. Design

resources required for the completion of new product

development, including internal organizations and

suppliers, are collectively referred to as generalized

design resources. General design resources are

limited, and always difficult to meet the growing

demand for new product development of the project

planning.

New product development of OEMs involves

collaborative multi-project management, which

comes to the rational allocation of limited generalized

design resources to collaboratively complete several

projects. Many famous experts and scholars have

referred to the design problems in resource sharing

and more collaborative project management.

Engwalla M qualitatively illustrated the sharing of

resources and implementation of concurrent

engineering combined to effectively work out the

allocation of resources, yet no solution was presently

given to a specific quantitative model. Chen You-

Ling , based on a key chain, put forward a method for

preparing a multi-project program, which gives a

comprehensive consideration on human factors and

resource constraints and other uncertainties. It

involves the use of critical chain planning methods in

scheduling the bottleneck and non-bottleneck project

plans. However, the method does not make a concrete

analysis of resource constraints that may affect the

several planning aspects. However, their further study

stopped at the design development process regarding

the reasonable allocation of resources and the

progress control of projects.

In the process of new product design and

development, multi-project coordination means the

scheduling for the allocation of resources for different

tasks, which falls in the Flow-shop Scheduling

Problem (FSSP). This is a typical problem called N-P,

for which the optimal solution can be sought through

the integer programming and branch & bound

method. But for some large or medium-scale

problems, the method can be quite difficult in

realization. In this paper, the genetic algorithm theory

was used to propose the match model for multi-

231

Deng X. and Guo G..

THE MATCHING FOR THE MULTI-PROJECT COLLABORATIVE PLAN OF NEW PRODUCT DEVELOPMENT AND RESOURCE BASED ON

GENERALIZED RESOURCE UNIT.

DOI: 10.5220/0003412502310234

In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 231-234

ISBN: 978-989-8425-54-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

project plan and resources particle under the

generalized resource constraints, and including its

optimization algorithms.

2 DEFINITION OF

GENERALIZED DESIGN

RESOURCE PARTICLES

Resource particles for new product design are

referred to the available entities comprised of the

people, computer hardware and software, and

information resources. Generalized design resource

particles come from the design resource particles of

the OEMs and suppliers, and the characteristic

attribute can be defined as ID number, name,

profession, job title, skill type (including software

skills), capacity factor, load status, and duration of

contract, performance and work units, etc. In the

new multi-project collaboration in product

development, the OEM resource particles are

generally used to complete the overall design of

products or components, system integration and the

management of suppliers. Particles of supplier

design resources are generally used to complete the

design of parts or components, driven by the tasks

assigned by OEMs. Thus, in product design and

development by multi-project collaborative

planning, each task needs to match a resource

particle, e.g. product design tasks need to match a

resource particle of the overall design capacity.

Once the matching is obtained, design resource

particles would have a state of load that is already

occupied in the task completion time, and no longer

to participate the matching of the remaining tasks in

this session. The matching relation is defined as the

constraint matching.

Design resource particles have symbols that are

defined as follows:

is No. j design resource

particle that belongs to OEMs, with No. i skill type;

is No. j design resource particle that belongs to

No. k supplier, with No. i skill type.

3 OPTIMAL SCHEDULING

ALGORITHM FOR

MULTIPROJECT

COORDINATED PLANNING

3.1 Definition of Variables

A triple MRA=(P,R,D)is employed for formal

description of constrained matching between multi-

project coordination plans and resource particles,

where each tuple is defined as follows.

P(Project)is a project set (set with m projects), as:

(

)

{

}

,,,,

iii iniiii

P A A A ES LF SS SF= …

(1)

Where,A

(1≤j≤n

) is No. j task in the No. I

project; ES

is the earliest starting time for the No. i

project; LF

is the latest end time for the No. i

project; SS

is the actual starting time for No.i

project; SF

is the actual end time for No. i project.

R=(R

) (Resources) is the set of resource

particles,. Then, resource particles are defined as:

{

}

,, []],1

xxxx

GSESWT x k

≤≤

(2)

Where, k is the number of particles in the

generalized design resources. It is assumed that a

type of resource particle can undertake the work in a

task type, and totaling e task types, G

∈{1,2,…e};

is the type identification of resource particles. It

is assumed that there are a total of f types, then SE

∈ {1,2,…f};SW

[T] array record indicates the

work schedule of No. x resource particles. Here, T is

the total number of days for planning. e.g.

[4]=33, indicates that in the fourth day of

program, No. x resource particle is allocated to task

D(Demands) is a collection of resource

requirements. The resource requirements matrix is

defined as:

11 12 1 , 1

21 22 2 , 2

12 ,

mm mnm

DD D

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

…



…

(3)

(1≤i≤m, 1≤j≤n

) is resource requirement

of No. j task A

in No. iproject ,D

=(TP

,SE

);

Where, TP

is the type of task A

∈{1,2,…e}; SE

∈{1,2,…f},indicates the type

identification of the resource particle required by task

is the duration for the task A

The assumption is often made for the Flow-Shop

issue: Each project shares the same number of tasks,

processes (i.e. the relationship between pre-task and

post-task); each of resource particles can only

undertake a task in the same time; each task only

needs to be allocated with an appropriate resource

particle.

3.2 Calculation of Optimum Solution

based on Genetic Algorithm for the

Sorting Queue of Tasks

Genetic algorithm is regarded as the simulation on

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

232

the biological evolution, and it borrows from

biological natural selection, without relying on the

random search algorithm from gradient information.

It is characterized by groups of search strategy and

the information exchange between individuals in

groups, suitable for complex nonlinear issues that

may be difficult to solve using traditional search

methods. However, it is not easy for genetic

algorithms to create the coding method to express

sufficient genetic information, and the calculation

method for the design of evaluation on the

individual fitness function.

3.2.1 Encoding Rules

As multi-project coordinated planning has no

priority difference between the projects, all tasks are

given the resources in the order that is the key to

planning. Each individual coding contains a

sequence message, which comes from more than one

task matching resources in different projects. It is

encoded in the form of a number string, totaling

∑

digital bits (m is the number of projects, n

is the

number of tasks in project i, with the 16-band being

used. If m>16, the encoding digit is doubled. If two

of 16 hexadecimal numbers are used as a processing

unit, and then 255 issues can be handled for

planning.) As required, the character string is

randomly generated, each number being appeared

for a number of times equal to the number of tasks

for the corresponding projects. The coding number

is the sequence of the various tasks with the

allocation of resources in the program. For example,

the digital string: "13123 ...." contains the task

scheduling order as indicated in Table 1:

Table 1: The encoding rule.

CODE

Task

scheduling

Remarks

1 A

The task in project 1. ‘1’ comes first,

indicating the task 1 in project 1

The task in project 3. ‘3’ comes first,

indicating the task 1 in project 3

The task in project 1. It comes for

the second time , indicating the task

…

… …

3.2.2 Fitness Function Value

Each of the scheduling programs is calculated on the

actual start time and actual end time SS

and SF

for

the projects. Scheduling objective is to calculate the

scheduling order of some task. Prior to the arrival of

landmark nodes, the projects in fine match should be

done as far as

possible, that is, the project that is desired to

finally end has the shortest period of time, that

is:min(max(SF

)),i=1,2,…m .For the need of sample

selection in roulette, the sample with a larger fitness

function value may have the larger probability to be

selected. So No. x code is constructed with the

corresponding fitness function value as:

(

)

(

)

max( )

fx U SF=−

(4)

Where, U is a sufficiently large number. This

algorithm is done to seek an optimal engineering

solution, obtaining the value of fitness function f(x)

that is largest in all samples.

3.2.3 The Algorithm Flow

The Crossover probability and mutation probability

can be estimated that the actual situation of the

project. The crossover rule indicates the use of

single-point crossover, and the exchange of all

digital cross bits behind the two samples. The

mutation rule requires values to be added with 1,

overloaded to return 1, namely:1→2,2→3…,m→1.

4 NUMERICAL EXAMPLE

AND VERIFICATION

A cell phone manufacturer is responsible for both of

the design and production of packaging materials to a

variety of mobile phones. The design and

development process is designed as: the mobile

phone manufacturer (OEMs) to design package

materials

→Supplier 1 to design packaging materials

mold

→

Supplier 1 for the mold

assembly

→ Supplier 2 for proofing → the mobile

phone manufacturer, for acceptance of package

materials and tooling. At this point, the multi-

collaborative project management model is formed

around the mobile phone manufacturer for design

and manufacture of packaging materials.

It is assumed that there are four ongoing

development projects of mobile phone package

materials, each project required to complete five

tasks according to the above process. Task types

include: 1. Package materials design. 2. Mold

assembly. 3. Proofing. 4. Acceptance. There are six

design resource particles ( of which resource particles

, M

and M

are OEM designers, with the

resource category identified as 1, here, M

and M

indicate the two particles to able to undertake the first

THE MATCHING FOR THE MULTI-PROJECT COLLABORATIVE PLAN OF NEW PRODUCT DEVELOPMENT

AND RESOURCE BASED ON GENERALIZED RESOURCE UNIT

233

task, that is, packaging materials design. M

is the

particle that takes the fourth task of acceptance. S

and S

are the resource particles of Supplier 1 to

takes the second task of the mold design and

assembly, with the particle class designation of 2.

is the resource particle of Supplier 2 to take on

No. 3 task, responsible for sampling, with the class

designation of 3. The OEM and suppliers have

different work sites.) The projects have the earliest

start time ES

, respectively as: ES

=1;

=4;ES

=9;ES

=12. 30 days are used as the time

for division of landmark nodes.



Date

Resourcesparticle

number

EndtimeofProject1

EndtimeofProject2

EndtimeofProject3

EndtimeofProject4

Thelastendtime:

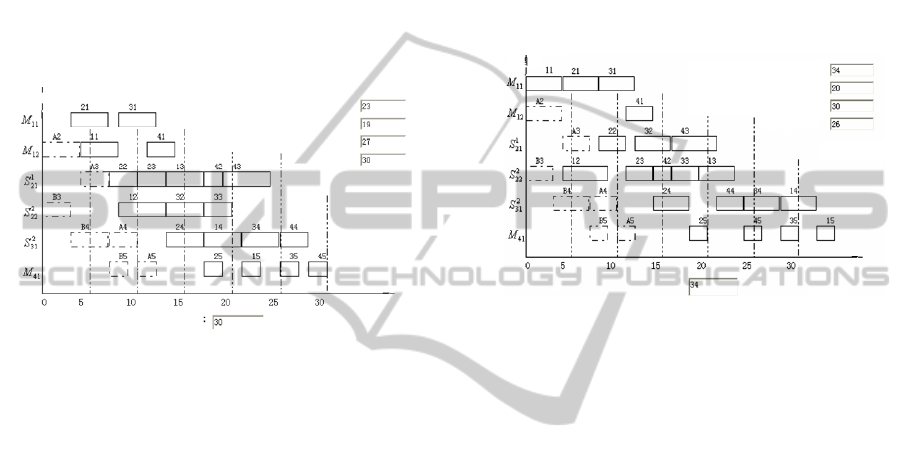
Figure 1: The result of optimized.

In preparing the plan of Session 1, there is part of

the task of the pre-task projects a, b are not

completed. Therefore, it is required to set resource

time occupied by these tasks as pre-occupied state, so

as not to participate in the task / resource matching in

the session, as shown in dashed boxes in Figure 1

and 2.

Set the crossover probability as 0.4, mutation

probability as 0.1. Through genetic optimization, an

optimal engineering solution is sought out. 20 tasks

(4 × 5) have the order to allocate resource particles

that are encoded as: "22121241284841144888". The

multi-project coordination plan is prepared based on

the optimum project solution, and the resource

particles have the Gantt work chart as shown in

Figure 1. The results show that the last ending project

is Project 4, with the end time of 30 days. That

happened to be completed the fine distribution of all

project plans prior to the arrival of landmark nodes.

Figure 2 is a comparison program that is not

optimized, and the sequence for the task allocation of

resources is a randomly generated number string (the

string is randomly generated on demand, each

number appearing for the number of times equal to

the task number of the mapping projects):

41248812284842482111. In that order for allocation

of resource particles, each of the resource particles

come out with the Gantt work chart as shown in

Figure 2, where the total time is 110 days, with

Project 4 being the finalized one, in 34 days. If the

plan multi-project coordination is prepared in

accordance with the program without optimization,

then prior to the arrival of the final landmark node, it

is not likely to complete all projects. The optimum

solution obtained by using optimization algorithm

was completed with a higher efficiency than the

randomly generated programs.



Resources

particlenumber

EndtimeofProject1

EndtimeofProject2

EndtimeofProject3

EndtimeofProject4

Thelastendtime:

Date

Figure 2: The contrastive result.

ACKNOWLEDGEMENTS

Supported by the National High Technology

Research and Development Program of China(863

Program,2007AA04Z1B1,and The Research

Foundation of Chongqing University of Science &

Technology, CK2010B10。

REFERENCES

Sun Qing-Chao, Guo Gang., 2008. Project Management

for Multi-Product Collaborative Development. In

Computer Integrated Manufacturing System.

Engwalla M, Jerbrantb A. 2003. The Resource Allocation

Syndrome: the prime Challenge of Multi-project

International Journal of Project Mangement

Chen You-Ling. 2009. Zhang Xiao-Li. Preparation of

Multi-Project Program based on A Key Chain.

Computer Integrated Manufacturing System

Zhao Xiao-Yuan, Jing Ji-Peng.

2005. Evaluation Index

System for Allocation Efficiency of Enterprise

Information Resources and the Empirical Study.

Information Technology

Wang Li, Chen Xing-Pan. 2007. Project Management for

Product Development and its Application in Product

Data Management. Computer Integrated

Manufacturing Systems.

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

234