
PATTERNS IDENTIFICATION FOR HITTING ADJACENT KEY
ERRORS CORRECTION USING NEURAL NETWORK MODELS
Jun Li
Department of Land Economy, University of Cambridge, 19 Silver Street, Cambridge, U.K.
Karim Ouazzane, Sajid Afzal, Hassan Kazemian
Faculty of Computing, London Metropolitan University, London, U.K.
Keywords: QWERTY Keyboard, Probabilistic Neural Network, Backpropagation, Key Distance, Time Gap, Error
Margin Distance.
Abstract: People with Parkinson diseases or motor disability miss-stroke keys. It appears that keyboard layout, key
distance, time gap are affecting this group of people’s typing performance. This paper studies these features
based on neural network learning algorithms to identify the typing patterns, further to correct the typing
mistakes. A specific user typing performance, i.e. Hitting Adjacent Key Errors, is simulated to pilot this
research. In this paper, a Time Gap and a Prediction using Time Gap model based on BackPropagation
Neural Network, and a Distance, Angle and Time Gap model based on the use of Probabilistic Neural
Network are developed respectively for this particular behaviour. Results demonstrate a high performance
of the designed model, about 70% of all tests score above Basic Correction Rate, and simulation also shows
a very unstable trend of user’s ‘Hitting Adjacent Key Errors’ behaviour with this specific datasets.
1 INTRODUCTION
Computer users with disabilities or some elderly
people may have difficulties in accurately
manipulating the QWERTY keyboard. For example,
motor disability can cause significant typing
mistakes. These issues haven’t been well addressed
by current technologies. Although alternative input
devices or software such as keyguard and Dasher are
available for use, none of them prove more efficient
or comfortable than the conventional QWERTY
keyboard. Some efforts associated with standard
keyboard has been made such as Windows’
Accessibility Options, ProtoType, however the
solution to remedy typing difficulties encountered
by disabled people hasn’t been achieved as yet.
Ouazzane and Li (2008) provide a
comprehensive report and classified user
performance as four categories, i.e. Motor disability,
Dyslexia, Unfamiliar with Computer and Others
performance. The ‘Miss-stroke’ or ‘Press Additional
Keys’ error is classified as sub-category three within
category one. However, in the paper only a brief
model framework is given based on multi-
technologies to tackle the typing errors as a whole,
while there is no specific solution and convincing
results for solving the ‘Miss-stroke’ error.
In the field of computer science, a neural
network is a mathematical model or computational
model that is inspired by the structure and/or
functional aspects of biological neural networks.
Modern neural networks are non-linear statistical
data modeling tools. They are usually used to model
complex relationships between inputs and outputs or
to find patterns in data. There are three major
learning paradigms, i.e. supervised learning,
unsupervised learning and reinforcement learning,
while BackPropagation is a supervised learning
method and most popular used in practice. It is an
implementation of the Delta rule, whose architecture
belongs to feedforward network. Probabilistic
Neural Networks (PNN) is a type of radial basis
network suitable for classification problems. It is a
feedforward network built with three layers, and
offers a series of advantages, including rapid
training speed, incremental training, and robustness
to noisy examples.
5
Li J., Ouazzane K., Afzal S. and Kazemian H..
PATTERNS IDENTIFICATION FOR HITTING ADJACENT KEY ERRORS CORRECTION USING NEURAL NETWORK MODELS.
DOI: 10.5220/0003413700050012
In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 5-12
ISBN: 978-989-8425-54-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

In the following sections, a Time Gap model and
a Prediction using Time Gap model based on
BackPropagation are developed respectively to
verify the influence of parameters such as keyboard
layout, key distance and time gap on human typing
behaviour. Then, an innovative model named
Distance, Angle and Time Gap model based on
Probabilistic Neural Network is developed to
simulate and predict a specific user typing behaviour
– ‘Hitting Adjacent Key Errors’ as a pilot research.
2 TIME GAP MODELLING
From Fitts’law (Fitts, 1954), users input
performance IP in bits per second is proportional to
the variable movement time ID, which has a direct
relation with the moving distance from one point to
another. Let’s consider a standard keyboard layout,
the time gap between two consecutive strokes
directly depends upon the distance between those
two keys. As observed, the last key’s position
represented by the distance and angle with the target
typing key could affect some of the disabled users’
judgment on their typing accuracy and speed, which
would be reflected by the time gap recorded on the
computer log. Given the user’s typing history, a 1-
gram neural network model named as Time Gap
Neural Network (TGNN) is designed here to
simulate and predict the two consecutive typing
letters’ time gap. A typical structure of generated log
is shown below.
Figure 1: Example structure of a generated log.
It is extracted from a charity helpline keystroke
log. The associated computer is routinely used as a
question recording, database query and email writing
tool by a disabled volunteer. From the reflected
keystroke log, the typing mistakes are predominantly
about adjacent key press errors. The keystroke
recording tool used in this research is KeyCapture
software(Soukoreff and MacKenzie, 2009), which
has been modified and adjusted for the purpose of
this research. It runs in background under Windows
environment to collect keystrokes without
interfering with user’s work.
A function - OnBnClickedsuggesttimegap is
programmed to pre-process the dataset. A fifty-four
virtual key codes set is considered, which includes
fifty-three visible symbols such as alphabet,
numbers and space. The other symbols are classified
as an assumed symbol - ‘Other’.
OnBnClickedsuggesttimegap function only
extracts the keystrokes whose time gaps is in a range
of [0, 3000] ms. The rest keystrokes which have
been considered as either out of range or computer
system related problems are ignored. 2-gram dataset
is created with their corresponding time gaps. This
requires 108 (i.e. NumberOfSymbols * Gram)
neurons in the input layer. All the time gap values
are normalized into a range of [-1, 1] according to
Min-Max Normalization before they are used by the
Time Gap Neural Network model (TGNN). The
normalization equation is shown below,
min max min max min min
' = ( )*( ' ' )/( ) + 'vvV V V VV V
−
−−
(1)
Where
max min
'1,' 1VV
=
=−
and variable v is the
time gap value extracted from the dataset. The
results of TGNN model will be reversed to their
natural values based on the same equation.
Then, a traditional BackPropagation neural
network is designed with a 108-7-1 three layer
structure. The input includes two consecutive
symbols represented by unary codes, and the output
is the expected time gap between these two
consecutive symbols. MATLAB neural network
toolbox is used for programming. The ‘tansig’ and
‘purelin’ functions are considered as the hidden and
output layer’s activation function.
A reconstructed dataset extracted from the log
file is used as neural network’s training dataset;
another two datasets, i.e. English alphabets in an
alphabetical order and QWERTY keyboard layout
order respectively, ‘abcdefghijklmnopqrstuvwxyz’
and ‘qwertyuiopasdfghjklzxcvbnm’, are used as two
testing cases. The experimental results generated by
TGNN model then demonstrated on these two
datasets are shown in Figure 2 and 3.
Firstly, the TGNN (Time Gap Neural Network)
model is trained based on the log file. Then the
Alphabet and QWERTY sequences are applied to
the TGNN model. Figure 2 shows a simulation of
the user’s typing behaviour (e.g. speed and time gap)
by typing an Alphabet sequence; Figure 3 shows a
simulation of the user’s typing behaviours (e.g.
speed and time gap) by typing a QWERTY
sequence. Due to no predecessors, both
corresponding time gaps of the first keystrokes in
sequence (in Figure 2 is ‘a’; and in Figure 3 is ‘q’)
are counted as zero.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
6

Figure 2: Modelling time gap using AÎZ sequence.
Figure 3: Modelling time gap using QWERTY sequence.
In Figure 2 and 3, x-axis represents user’s typing
sequence; y-axis represents the time gap in
milliseconds. Between each two consecutive
alphabets, a blue line is drawn to illustrate the
elapsed time. The maximum time gap (637.4ms)
occurs in Figure 2 when the finger moves from key
‘x’ to ‘y’; while the minimum time gap (89.9ms)
appears in both figures, when the finger moves from
‘j’ to ‘k’.
These two figures show that the current
keystroke’s predecessor affects the user’s typing
behaviour (e.g. time gap) if one ignores the user’s
keystroke action itself and behaviour randomicity
that human may have. Due to the distance difference
between each two keys in computer QWERTY
keyboard, the time gap of each two consecutive keys
during user strokes varies.
The red lines in Figure 2 and 3 represent the
average time cost of all twenty-five movements,
which show that the cost of typing an alphabet order
sequence is 384.44ms (see Figure 2), whereas the
cost of typing a QWERTY order sequence is
342.50ms (see Figure 3). The test shows typing an
Alphabet sequence is more time consuming based on
a standard keyboard. This can be explained by
movement cost, meaning that an alphabet order
sequence would require more time for a user to
locate the keys from one to another.
This research gives a glance at the idea that the
Time Gap between two consecutive keystrokes is
influenced by current symbol’s predecessor. A
further research tracing back more than one gram
history accompanied with a larger dataset is
necessary.
3 PREDICTION USING TIME
GAP
As mentioned in the introduction, people with motor
disability or Parkinson disease using keyboard may
press adjacent keys or stick keys. These can be
shown from the time gap between each two
consecutive key strokes. For example, a time gap
between the windows keyboard messages caused by
sticking keys can be much smaller than the user’s
normal typing speed; the opposite case may also
happen when more time can be spent by disabled
people aiming at the target before making up their
mind. From observation, interestingly it is rare for
those people to completely miss typing a symbol.
According to these distinct behaviours, a neural
network model using BackPropagation (newff) is
designed by adding an extra Time Gap variable in
the input layer, called Prediction using Time Gap
(PTG). Here, a small sample typed by a Parkinson
person is used to demonstrate the idea. The target
typing sample is,
the quick brown fog jumped over the lazy dog
The user’s true typing sample is,
hthe quick brrooownn fgow jummppefd
iobverethe lwqazy dooggfg
The typed sample is reconstructed for
preprocessing,
@the quick br@o@@wn@ @@f@ox@
jum@p@e@d @@o@ver the l@@azy
do@g@@@
Where the symbol ‘@’ represents an error or a
NULL, compared to the right sample which should
be recognized by PTG model. During preprocessing,
the time gap value which is one of the input
PATTERNS IDENTIFICATION FOR HITTING ADJACENT KEY ERRORS CORRECTION USING NEURAL
NETWORK MODELS
7
parameters is categorized into three levels and
converted into three bits unary codes. In this case,
‘<= 10 milliseconds’ over-fast => 001
‘10< && <=1000 milliseconds’ user-Speed => 010
‘>1000 milliseconds’ over-slow => 100
The user’s typing has been recorded both by
Notepad and KeyCapture software.
Prediction using Time Gap model is designed
with three layers 30-7-28 structure, where the input
requirement of PTG model is twenty seven length
unary coding symbol {‘a’…’z’, space} and three
length unary coding time gap, and the output
requirement is twenty eight length unary coding
limited in symbol set {‘a’…’z’, space, ‘@’}, where
the symbol ‘@’ is added to represent an additional
or missed symbol.
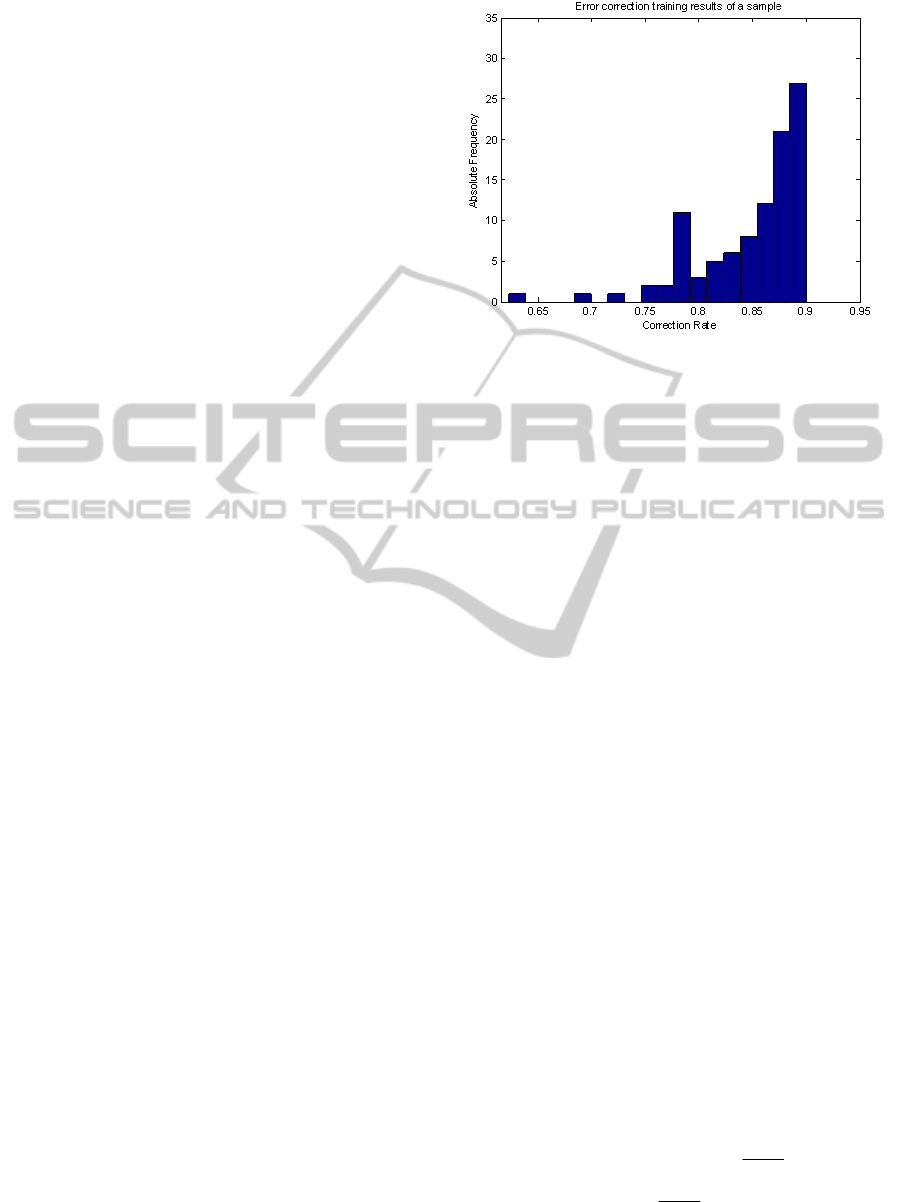
The correction rate distribution within one
hundred times training is shown in Figure 4, which
has a mean value of 0.8480 and a deviation of
0.0501. The x-axis represents the correction rate
based on the comparison between the target dataset
and PTG generating dataset; the y-axis represents
the absolute frequency of the one hundred times
training results, which illustrates the number of
times a particular outcome occurs.
Figure 4 demonstrates the range that PTG
model‘s correction rate lies on. It shows that the
results lie predominantly between 65% and 90%.
Under this test sample there is about twenty-seven
times where the correction rate has reached near
90% and only once the correction rate happens to be
less than 65%.
This test indicates that the time gap can be
considered as an input element used by neural
network model to correct wrong typed symbols. Due
to no gram consideration and the size limitation of
training dataset, the relationship built between input
and output is a pure right-wrong relationship. This
could lead to a further research on the n-gram
language modelling with larger training and testing
dataset.
4 PROBABILISTIC NEURAL
NETWORK MODELLING
♦ Assumption: the research carried out in
this section is based on one finger typing
user case. User’s each key press and move
rely entirely on a single finger. Skilful
users’ typing behaviour in controlling
Figure 4: Absolute Frequency of PTG model Correction
Rate.
fingers may vary, and the distance of
fingers move between two consecutive
keystrokes could be more complex.
♦ Key Distance Definition: according to the
layout of a computer QWERTY keyboard,
there exists a physical distance between
each two keys. Let
,ij
d be the distance
between key i and key j, and define the
measure unit as key-distance. Then,
,
1
as
d
=
shows that the distance between
key ‘A’ and key ‘S’ is one key-distance;
,
3
af
d
=
means there are three key-
distances between key ’A’ and key ‘F’.
Users move their fingers toward the next
key as soon as they finish current key
press. The distance between two keys
affects a user’s typing performance.
♦ Error Margin Distance (EMD)
Definition: based on Key Distance, a
variable
,
s
f
dΔ is further defined as a
distance between a user’s typed key -
s
key and target key -
f
key and called
Error Margin Distance. The Error Margin
Distance is mainly caused by the user’s
‘Hitting Adjacent Key Error’.
♦ Key Distance Class Definition: let’s
define a class,
,
{|}
i
key j ij i
C key key= , by
giving
1
, { ,..., }
iij n
key key key key∈ ,
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
8
where
,ij n≤ , n is the number of keys
related to a computer QWERTY keyboard,
ij
key represents a key set around
i
key
within j key-distances. For instance, a one
key-distance set corresponding to key ‘s’
is,
,1 1
{ | } {' ',' ',' ',' ',' ',' '}
s
CssDEWAZX=≈
Noisy data prediction models such as Focused Time-
Delay Neural Network not only can be generally
used to analyze a language text, but also can be
explored to analyze some specific problems. For
example, let’s take the helpline data as a real
scenario. As shown in the data, a typist is frequently
making ‘Hitting Adjacent Key Errors’ mistakes.
Therefore, all the typing mistakes are extracted from
the log file and used to identify the possible rules. A
sample of it is shown below,
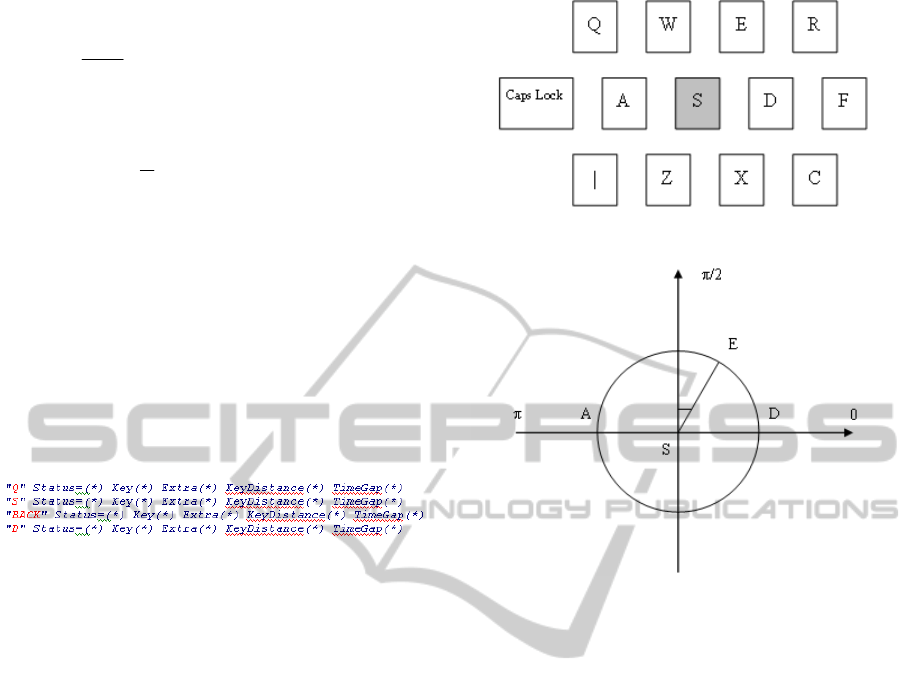
Figure 5: A sample of ‘Hitting Adjacent Key Errors’.
This is a typical ‘Hitting Adjacent Key Errors’
typing mistake that occurred within a user’s typing
stream. The user’s intention is to type a letter ‘d’
following letter ‘q’, but the letter ‘s’ is mistakenly
pressed. So the user has to go back and make a
correction by pressing ‘backspace’ key shortly after
the mistake is made (in virtual key code, the
‘backspace’ is represented by ‘BACK’). Both Key
Distance and Time Gap are calculated and recorded
in the log.
The user investigation shows users’ Hitting
Adjacent Key behaviour is related to the positions of
both the last key and the current key if one ignores
the stroke randomicity that users’ symptoms may
cause. It also shows that a user’s typing speed
moving from one key to another also plays an
important role in making such errors. For example,
although a faster typing speed than a user’s normal
speed increases the occurrence of ‘Hitting Adjacent
Key Errors’, the users’ hesitation which leads to
much slower typing speed does not always help to
an increase of right typing rate, as shown in the log
file.
Here, the idea is to use these essential
parameters, namely, Key Distance, Time Gap and
Error Margin Distance to discover the fundamental
rules behind uses’ typing mistakes. Let’s start with
the introduction of QWERTY keyboard layout, and
consider Figure 6 and 7,
Figure 6: A QWERTY keyboard layout sample.
Figure 7: Relationship – angle between keys and its
surrounding keys D, E, A.
In Figure 6, key ‘S’ is surrounded by one key-
distance dataset {‘W’, ‘E’, ‘A’, ‘D’, ‘Z’, ‘X’} and two
key-distance dataset {‘Q’, ‘R’, ‘caps lock’, ‘F’, ‘|’,
‘C’}. Given certain inputs, if one requires the neural
network model to be able to produce the right
symbol that a user intends to type, the designed
model not only need to deduce the dataset which the
right symbol belongs to, but also the right angle the
user intends to move towards. This is illustrated in
Figure 7. All keys surrounding ‘S’ are positioned
with different angles. Let’s assume the circle starts
from right-hand side of ‘S’ and turns in an
anticlockwise direction. Then the key ‘D’ can be
expressed by a three dimensions vector,
d
key =
{key=’S’, distance=1, angle=0}, where key=’S’
illustrates the dataset surrounding key ‘S’,
distance=1 & angle =0 represent the key which is
one key-distance away from key ‘S’ with an angle of
zero degree. The key ‘A’ can be expressed as
a
key
= {key=’s’, distance=1, angle=π}, distance=1,
angle=π means the key is one key-distance away
from key ‘S’ with an angle of π degree.
The key distance and time gap between last two
grams could determine the error margin between the
wrong key and the right key. In order to prove this
PATTERNS IDENTIFICATION FOR HITTING ADJACENT KEY ERRORS CORRECTION USING NEURAL
NETWORK MODELS
9

hypothesis, a Neural Network Topology with
Distance, Angle and Time Gap vectors in the input
layer, and the Error Margin Distance vector between
the typed key and target key in the output layer is
designed. These require a precise measurement on
both input and output parameters. However, given
the difficulty of QWERTY keyboard and its
associated operating system to respond to an
accurate simulation of users’ movement and the
difficulty of a neural network to provide a precise
output, this solution, as it stands, is not practical.
For example, the difference in angle between key ‘S’
Æ key ‘E’ and key ‘S’ Æ key ‘R’ is not significant.
This high precision requirement raises the design
difficulty of a neural network model.
In order to overcome these obstacles, a more
robust neural network model with re-designed
vectors on both input and output layers is developed
in this research. The input of neural network model
uses (x, y) coordinate expression instead of distance
and angle, where x represents x-axis key-distance
(i.e. horizontal distance), and y represents y-axis
key-distance (i.e. vertical distance). X-axis key-
distance refers to a user’s horizontal move toward
the typed key; y-axis key-distance refers to a user’s
vertical move toward the typed key. The time gap
parameter is kept unchanged, which represents the
time difference (ms) between two consecutive key
strokes. When the error margin is calculated, the
coordinate centre lies at the current typed key. When
the distance of last typed key and current typed key
is calculated, the coordinate centre lies at the last
typed key. The sign of key distance will be
determined as soon as the coordinate centre is fixed.
In QWERTY keyboard there are maximum of
six one key-distance keys around each key. The user
investigation records suggest that most of ‘Hitting
Adjacent Key Errors’ occur in an area where the
keys are equal or less than one key-distance away
from the target keys. Therefore, instead of
computing a precise error margin
,tf
dΔ
, the output
of neural network model can be designed as a six-
classes classifier. If one counts the class in a wise-
clock direction according to traditional coordinate,
then, from Figure 7, ‘d’ belongs to class one, ‘e’
belongs to class two and so on. Thus the question
can be interpreted as finding an appropriate neural
network model to solve a classification issue
associated with input vectors: Distance, Angle and
Time Gap.
It is well known that radial basis networks can
require more neurons than standard feedforward
BackPropagation networks, but quite often they can
be designed in a fraction of the time it takes to train
standard feedforward networks. One of Radial basis
networks is Probabilistic Neural Networks (PNN)
which can be used for classification problems. As
PNN is a time-efficient and classification-solving
solution, in this research a 3-N-1 structure model,
i.e. Distance, Angle and Time Gap PNN model
(DATP model) is designed based on PNN to predict
where the target key could possibly lie against the
wrong key press.
The DATP model consists of three layers, input
layer, hidden layer and output layer. The hidden
layer – radbas layer compute the distance between
the input vector and the hidden weights vector, and
then produces a distance vector which indicates how
close the input is against the correct letter. The third
layer would classify the results of radbas layer and
produces the right class.
In this experiment, thirty three ‘Hitting Adjacent
Key Errors’ are identified from log file, and are
converted into the format training dataset manually.
At the same time another ten samples are used as
test samples. Here an example is given to show the
pre-processing procedure,
Figure 8: An example of pre-processing procedure.
The first four lines are extracted from log file.
The line following an arrow is the data transformed
manually from the lines above, which has four
parameters, namely, horizontal distance, vertical
distance, time gap between two consecutive
keystroke, and class.
The first line shows that the horizontal distance
from ‘C’ to ‘J’ is 3.5 key-distances, however, if the
move are from ‘J’ to ‘C’, the key-distance would be
-3.5; the vertical distance is one key-distance; the
time gap from ‘C’ to ‘J’ is 108ms (shown in red) and
the class is ‘4’ as the key ‘H’ is at the left hand side
of key ‘J’. In the case of overlapping keys, a half
key-distance can be counted. For example,
Figure 9: An example of overlapping keys pre-processing.
This is a typical key press with overlapped key
‘G’ and key ‘H’. The time gap between ‘G’ press
and ‘H’ press is 3ms, which is much less than the
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
10

user’s usual typing speed. This has been proved by
the user’s correction which happened afterwards, as
shown in the log file. The horizontal key-distance
between key ‘D’ and key ‘G’ is two key-distances,
however, another 0.5 key-distance is added in pre-
processing by taking into consideration the
overlapping. The vertical distance between these two
keys is zero, while the time gap is 218ms and the
output class is 4.
The experimental results show a correction rate
of 50% which is five out of the ten testing samples.
However, due to the highness of user’s typing
disorder and the small size of training dataset, a
random training and testing dataset selection
strategy is further adopted. The thirty three training
samples and ten testing samples are mixed up and
the random function iRand is applied to randomly
pick up the training dataset and testing dataset in a
proportion of 2/3 and 1/3 respectively. Two groups
of trials are carried out, and each group of them
includes ten training and testing samples. The
corresponding plots are shown in Figure 10.
The x-axis refers to training and testing samples
that are picked up randomly; the y-axis refers to the
prediction rate of the DATP model. The dashed line
in red shows the prediction rate of each testing
dataset according to its training dataset; the line in
blue is the random prediction rate which has been
named as Basic Rate.
The first plot of Figure 10 demonstrates that
there are six rounds out of eight whose prediction
rates are above Basic Rate, while the rest are below
Basic Rate. The highest score (40%) occurs at the
third round, while the lowest score occurs at eighth
round (0%). The second plot indicates that there are
seven rounds whose prediction rates are above Basis
Rate, while the three remaining rounds are below
Basic Rate. The highest score (36%) occurs at the
tenth round while the lowest score (7%) occurs at
the third round.
Both plots show that there are 70% of all tests
scoring above Basic Rate. They also demonstrate a
very unstable trend of user’s ‘Hitting Adjacent Key
Errors’ behaviour. It recommends that the training
dataset with a small size of data may not be able to
give a high prediction rate as the dataset has a bad
convergence. In that case, several rounds of training
with a random dataset selection strategy may be
required.
Further work to be carried out should focus on two
areas: the DATP model development with larger
scaled data to obtain a more accurate prediction rate,
and a touch keyboard combining the sensitivity of
Figure 10: Hitting Adjacent Key prediction rates based on
PPN network (the top and the beneath plots are generated
from group one and two trials respectively).
touch screen and functionality of QWERTY layout
to detect the users’ finger movement more precisely
to calculate the accurate
,
s
f
dΔ .
5 CONCLUSIONS
In this paper the influence of time gap on user’s
typing performance is studied, and a unique Time
Gap model is developed. Experimental results show
that the current keystroke’s predecessor affected the
user’s typing behaviour, and the Time Gap between
two consecutive keystrokes is influenced by current
symbol’s predecessor. Inspired by this conclusion, a
fundamental PTG model is developed. Its
experimental results indicate that the correction rates
predominantly lie in between 65% and 90% with the
current testing sample.
Furthermore, an innovative Distance, Angle and
Time Gap PNN model based on Probabilistic Neural
Network is developed to simulate a specific user
typing behaviour – ‘Hitting Adjacent Key Errors’
based on unique factors such as key distances.
Results demonstrate that about 70% of all tests score
above Basic Correction Rate. Results also show a
very unstable trend of user’s ‘Hitting Adjacent Key
Errors’ behaviour, which suggest that several
training trials with a random dataset selection
strategy could be applied.
PATTERNS IDENTIFICATION FOR HITTING ADJACENT KEY ERRORS CORRECTION USING NEURAL
NETWORK MODELS
11

ACKNOWLEDGEMENTS
The research is funded by Disability Essex and
Technology Strategy Board. Thanks to Richard
Boyd, Pete Collings and Ray Mckee for helpful
advice and discussions.
REFERENCES
Artificial neural network, [online], 31 Dec. 2010,
available: http://en.wikipedia.org/wiki/Artificial_
neural_network [12 January 2010]
David J. Ward, Alan F. Blackwell at el. (2000). ‘Dasher-a
Data Entry Interface Using Continuous Gestures and
Language Models’, UIST '00 Proceedings of the 13th
annual ACM symposium on User interface software
and technology
Disability Essex, http://www.disabilityessex.org [accessed
18 January 2009]
Karim Ouazzane, Jun Li and Marielle Brouwer (2008). ‘A
hybrid framework towards the solution for people with
disability effectively using computer keyboard’,
IADIS International Conference Intelligent Systems
and Agents 2008, pp. 209-212
Knowledge Transfer Partnership, http://www.
ktponline.org.uk/ [accessed 18 January 2009]
Paul M. Fitts (1954). ‘The information capacity of the
human motor system in controlling the amplitude of
movement’, Journal of Experimental Psychology,
volume 47, number 6, June 1954, pp. 381-391
Prototype, [online], n.d., available: http://www.sensory
software.com/prototype.html [accessed 03 March
2008]
R. W. Soukoreff, & I. S. MacKenzie, n.d. KeyCapture
[online], available: http://dynamicnetservices.com/
~will/academic/textinput/keycapture/ [accessed 18
January 2009]
R. W. Soukoreff, & I. S. MacKenzie (2003). ‘Input-based
language modelling in the design of high performance
text input techniques’, Proceedings of Graphics
Interface 2003, 89-96.
The Dasher Project, [online], 14 Nov. 2007, Inference
Group of Cambridge, available: http://www.inference.
phy.cam.ac.uk/dasher/ [accessed 03 March 2008]
Unary coding, [online], 23 December 2009, available:
http://en.wikipedia.org/wiki/Unary_coding [12
January 2010]
Virtual key codes [online], available:
http://api.farmanager.com/en/winapi/virtualkeycodes.h
tml [accessed 05 February 2009]
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
12
