
ON THE DISTRIBUTION OF SOURCE CODE FILE SIZES
Israel Herraiz
Technical University of Madrid, Madrid, Spain
Daniel M. German
University of Victoria, Victoria, Canada
Ahmed E. Hassan
Queen’s University, Kingston, Canada
Keywords:
Mining software repositories, Software size estimation, Open source.
Abstract:
Source code size is an estimator of software effort. Size is also often used to calibrate models and equations
to estimate the cost of software. The distribution of source code file sizes has been shown in the literature to
be a lognormal distribution. In this paper, we measure the size of a large collection of software (the Debian
GNU/Linux distribution version 5.0.2), and we find that the statistical distribution of its source code file sizes
follows a double Pareto distribution. This means that large files are to be found more often than predicted by
the lognormal distribution, therefore the previously proposed models underestimate the cost of software.
1 INTRODUCTION
Source code size is a simple, yet powerful metric
for software maintenance and management. Over the
years, much research has been devoted to the quest
for metrics that could help optimize the allocation
of resources in software projects, both at the devel-
opment and maintenance stages. Two examples of
these are McCabe’s cyclomatic complexity (McCabe,
1976) and Halstead’s software science metrics (Hal-
stead, 1977). In spite of all the theoretical consider-
ations that back up these metrics, previous research
shows that simple size metrics are highly correlated
with them (Herraiz et al., 2007), or that these met-
rics are not better defect predictors than just lines of
code (Graves et al., 2000).
Perhaps due to these facts, software size, rather
than many other more sophisticated metrics, has been
used for effort estimation. Standard models like
COCOMO are now widely used in industry to esti-
mate the effort needed to develop a particular piece of
software, or to determine the number of billable hours
when building software (Boehm, 1981).
In recent years, besides the previously mentioned
works, the statistical properties of software size have
attracted some attention in research. Recent research
shows that the statistical distribution of source code
file sizes is a lognormal distribution (Concas et al.,
2007), and some software size estimation techniques
built on that finding (Zhang et al., 2009). Some other
preliminary research conflicts with this finding for
the distribution of size, proposing that the statistical
distribution of source code file sizes follows a dou-
ble Pareto distribution (Herraiz et al., 2007; Herraiz,
2009).
All the mentioned works use publicly available
software, so they can be repeated and verified by third
parties. These are crucial aspects to determine with-
out further doubt which is the statistical distribution
of size. However, some of these studies (Zhang et al.,
2009; Concas et al., 2007) are based on a few case
studies, with the consequent risk of lack of generality,
opening the door to possible future conflicting stud-
ies. To overcome these drawbacks, we report here the
results for a very large number of software projects,
which source code have been obtained from the De-
bian GNU/Linux distribution, release 5.0.2. Our sam-
ple contains nearly one million and a half files, ob-
tained from more than 11, 000 source packages.
The main contributions of this paper are :
5
Herraiz I., German D. and Hassan A..
ON THE DISTRIBUTION OF SOURCE CODE FILE SIZES.
DOI: 10.5220/0003426200050014
In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 5-14
ISBN: 978-989-8425-77-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

• Software size’s distribution is a double Pareto
This implies that the distribution of software size
is a particular case of the distribution of the size
of filesystems (Mitzenmacher, 2004b), and it also
confirms previous results based on other case
studies (Herraiz et al., 2007; Herraiz, 2009).
• Estimation techniques based on the lognormal
distribution underestimate the potential size of
software
And therefore they underestimate its cost. We cal-
culate the bias of lognormal models compared to
the size estimated using a double Pareto model.
The rest of the paper is organized as follows. Sec-
tion 2 gives an overview of the related work. Sec-
tion 3 describes the data sources and the methodol-
ogy used in our study. Section 4 shows our approach
to determine the shape of the statistical distribution
of software size. Section 5 compares the lognormal
and double Pareto distributions for software estima-
tion, also showing how the lognormal distribution al-
ways underestimates the size of large files. For clar-
ity purposes, all the results are briefly summarized in
section 6. Section 7 discusses some possible threats
to the validity of our results. Section 8 discusses some
possible lines of further work. And finally, section 9
concludes this paper.
2 RELATED WORK
In the mathematics and computer science communi-
ties, the distribution of file sizes has been an object
of intense debate (Mitzenmacher, 2004a). Some re-
searchers claim that this distribution is a lognormal,
and some others claim that it is a power law. In some
cases, lognormal distributions fit better some empir-
ical data, and in some other cases power law distri-
butions fit better. However, the generative processes
that give birth to those distributions, and the possible
models that can be derived based on those processes,
are fundamentally different (Mitzenmacher, 2004b).
Power-laws research was already a popular topic
in the software research community. Clark and
Green (Clark and Green, 1977) found that the point-
ers to atoms in Lisp programs followed the Zipf’s law,
a form of power law. More recent studies have found
power laws in some properties of Java programs, al-
though other properties (some of them related to size)
do not have a power law distribution (Baxter et al.,
2006). But it is only in the most recent years when
some authors have started to report that this distri-
bution might be lognormal, starting the old debate
previously found for file sizes in general. Concas et
al. (Concas et al., 2007) studied an object-oriented
system written in Smalltalk, finding evidences of both
power law and lognormal distributions in its proper-
ties. Zhang et al. (Zhang et al., 2009) confirmed some
of those findings, and they proposed that software size
distribution is lognormal. They also derive some es-
timation techniques based on that finding, aimed to
determine the size of software. Louridas et al. (Louri-
das et al., 2008) pointed out that power laws might
not be the only distribution found in the properties of
software systems.
For the more general case of sizes of files of any
type, Mitzenmacher proposed that the distribution is
a double Pareto (Mitzenmacher, 2004b). This result
reconciles the two sides of the debate. But more inter-
estingly, the generative process of double Pareto dis-
tributions mimics the actual work-flow and life cycle
of files. He also shows a model for the case of file
sizes, and some simulation results. The same distribu-
tion was found in the case of software (Herraiz et al.,
2007; Herraiz, 2009), for a large sample of software,
although the results were only for the C programming
language.
The Debian GNU/Linux distribution has been the
object of research in previous studies (Robles et al.,
2005; Robles et al., 2009). It is one of the largest
distributions of free and open source software.
In the spirit of the pioneering study by Knuth in
1971 (Knuth, 1971), where he used a survey approach
of FORTRAN programs to determine the most com-
mon case for compiler optimizations, we use the De-
bian GNU/Linux distribution with the goal of enlight-
ening this debate about the distribution of software
size, extending previous research to a large amount of
software, written in several programming languages,
and coming from a broad set of application domains.
3 DATA SOURCE AND
METHODOLOGY
We retrieved the source code of all the source pack-
ages of the release 5.0.2 of the Debian GNU/Linux
distribution. We used both the main and contrib sec-
tions of distribution, for a total of 11, 571 source code
packages, written in 30 different programming lan-
guages, with a total size of more than 313 MSLOC,
and more than 1, 300, 000 files. Figure 1 shows the
relative importance of the top seven programming
languages in this collection; they account more than
90% of the files.
We measured every file in Debian, using the
SLOCCount tool by David A. Wheeler
1
. This tool
1
Available at http://www.dwheeler.com/sloccount
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
6

C C++ Shell Java Python Perl Lisp
% SLOC
0 10 20 30 40
Figure 1: Top seven programming languages in Debian
(representing 90% of Debian’s size). The vertical axis
shows the percentage of the overall size.
measures the size of files in SLOC, which is number
of source code lines, excluding blanks and comments.
Table 1 shows a summary of the statistical proper-
ties of this sample of files, for the overall sample and
for the top seven programming languages. Approxi-
mately half of Debian is written in C, and almost three
quarters of it is written in either C or C++. The large
number of shell scripts is mainly due to scripts used
for build, and installation purposes; shell scripting is
present in about half of the packages in Debian.
We divided the collection of files into 30 groups,
one for each programming language and another one
for the overall sample, and estimated the shape of the
statistical distribution of size. For this estimation, we
plotted the Complementary Cumulative Distribution
Function (CCDF) for the top seven programming lan-
guages. The Cumulative Distribution Function (CDF)
is the integral of the density function, and its range
goes from zero to one. The CCDF is the complemen-
tary of the CDF. All these three functions (density
function, CDF and CCDF) show the same informa-
tion, although their properties are different. For in-
stance, in logarithmic scale, a power law distribution
appears as a straight line in a CCDF, while a lognor-
mal appears as a curve. So the CCDF can be used
to distinguish between power laws and other kind of
distributions.
In a CCDF, the double Pareto distribution appears
as a curve with two straight segments, one at the low
values side, and another one at the high values side.
The difference between a lognormal and a power law
at very low values is negligible, and therefore imper-
ceptible in a plot. This means that in a CCDF plot
the main difference between a lognormal and a dou-
ble Pareto is only spotted at high values. In any case,
for our purposes, it is more important to focus on the
high values side. A difference for very small files
(e.g. < 10 SLOC) is harmless. However, a difference
for large files (e.g. > 1000 SLOC) may have a great
impact in the estimations.
To estimate the shape of the distribution, we use
the method proposed by Clauset et al. (Clauset et al.,
2007); in particular, as implemented in the GNU
R statistical software (R Development Core Team,
2009). They argue that power law data are often fit-
ted using standard techniques like least squares re-
gression, that are very sensible to observations cor-
responding to very high values. For instance, a new
observation at a very high value may greatly shift the
scaling factor of a power law. The result is that the
level of confidence for the parameters of the distribu-
tion obtained using those methods is very low.
Clauset et al. propose a different technique, based
on maximum-likelihood, that allows for a goodness-
of-fit test of the results. Furthermore, their technique
can deal with data that deviate from the power law
behavior for values lower than a certain threshold,
providing the minimum value of the empirical data
that belongs to a power law distribution. For double
Pareto distributions, that value can be used to calcu-
late the point where the data changes from lognormal
to power law. That shifting value can be used to de-
termine at what point the lognormal estimation model
starts to deviate from the actual data, and to quantify
the amount of that deviation.
4 DETERMINING THE SHAPE
OF THE SIZE DISTRIBUTION
As Table 1 shows, evidenced by the difference be-
tween the median and the average values, our data is
highly right skewed. This is typical of lognormal or
power law-like distributions. There exist many differ-
ent methods to empirically determine the distribution
of a data set. Here we use a combination of different
statistical techniques, to show that in our case, that
the studied size distribution is a double Pareto one.
We first show some results for the global sample, and
later we will split our results by programming lan-
guage.
Histograms are a simple tool that can help to find
the distribution behind some data. When the width of
the bars is decreased till nearly zero, we have a den-
sity function, that is a curve that resembles the shape
of the histogram. Although a density function is only
defined for continuous data, we can estimate it for our
discrete data, and use it to determine the shape of the
distribution. For the case of our sample, that function
is shown in Figure 2. Note that the horizontal axis
shows SLOC using a logarithmic scale.
Because our data are integers values and discrete,
the estimation of the density function tries to inter-
polate the missing values, showing some “jumps” for
ON THE DISTRIBUTION OF SOURCE CODE FILE SIZES
7

Table 1: Properties of the sample of files. Values in SLOC.
Lang Num. of files Max. Avg. Median Total
Overall 1, 355, 752 765, 108 231 63 313, 774, 217
C 498, 484 765, 108 306 85 152, 368, 424
C++ 332, 652 172, 487 193 58 64, 267, 501
Shell 66, 107 46, 497 409 62 27, 038, 314
Java 158, 414 28, 784 109 43 17, 334, 539
Python 63, 590 65, 538 156 59 9, 888, 159
Perl 48, 055 58, 164 188 69 9, 037, 066
Lisp 21, 101 105, 390 373 132 7, 870, 134
1e+00 1e+02 1e+04 1e+06
0.00 0.10 0.20
SLOC
Density
Figure 2: Density probability function for the overall sam-
ple. Horizontal axis shows SLOC in logarithmic scale.
−4 −2 0 2 4
0 2 4 6 8 10
Theoretical Quantiles
Sample Quantiles
Figure 3: Quantile-quantile plot of the overall sample. Log-
arithmic scale.
very low values. The most important feature is that
it shows that the logarithm of size is symmetric, and
that the shape of the curve somehow resembles a
bell-shaped normal distribution, meaning that the data
could belong to a lognormal distribution.
To determine whether the data is lognormal or not,
we can compare its quantiles against the quantiles of
a theoretical reference normal distribution. Such a
comparison is done using a quantile-quantile plot. An
example of such a plot is shown in Figure 3,
In that plot, if the points fall over a straight line,
they belong to a lognormal distribution. If they do
1 10 100 1000 10000
1e−04 1e−02 1e+00
SLOC
CCDF
Figure 4: Complementary cumulative distribution function
of the overall sample.
not, then the distribution must be of another kind. The
shape shown in Figure 3 is similar to the profile of a
double Pareto distribution. The main body of the data
is lognormal, and so it appears as a straight line in the
plot (the points fall over the dashed line that is shown
as a reference). Very low and very high values deviate
from linearity though. However, with only that plot,
we cannot say whether the tails are power law or any
other distribution.
Power laws appear as straight lines in a
logarithmic-scale plot of the cumulative distribution
function (or its complementary). Therefore, combin-
ing the previous plots with this new plot, we can fully
characterize the shape of the distribution. Figure 4
shows the logarithmic-scale plot of the complemen-
tary cumulative distribution function for the overall
sample. The main lognormal body clearly appears
as a curve in the plot. The low values hypothetical
power law cannot be observed, because at very low
values the difference between a power law and a log-
normal is negligible. The high values power law does
not clearly appear either. It seems that the high values
segment is straight, but at a first glance it cannot be
distinguished from other shapes.
Using the methodology proposed by Clauset et
al. (Clauset et al., 2007), we estimate the parame-
ters of the power law distribution that better fit the
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
8
Table 2: Parameters of the power law tails for the top seven
programming languages and the overall sample.
Lang. α x
min
D p
Overall 2.73 1, 072 0.01770 0.1726
C 2.87 1, 820 0.01694 0.5349
C++ 2.80 1, 258 0.01202 0.5837
Shell 1.71 133 0.13721 ∼ 10
−14
Java 3.17 846 0.01132 0.6260
Python 2.90 826 0.01752 0.2675
Perl 2.23 137 0.02750 ∼ 10
−5
Lisp 2.73 1, 270 0.01996 0.5229
tail of our data, and calculate the Kolmogorov dis-
tance, a measure of the goodness of fit. We can also
calculate the transition point at which the data stops
being power law. In the following, we will refer to
that point as the threshold value. With that threshold
value, we can separate the data in at least two different
regions: data which follows a lognormal distribution
and data which follows a power law distribution. The
values estimated for the top seven programming lan-
guages are shown in Table 2. It also includes the p
values resulting from the hypothesis testing, using the
Kolmogorov-Smirnov test.
The second column is the scaling parameter of
the power law. The third column is the threshold
value: files with sizes higher than that value belong
to the power law side of the double Pareto distribu-
tion. The fourth column is the Kolmogorov distance.
It is the maximum difference between the empirical
CCDF and the CCDF of the power law with the es-
timated parameters. Lower values indicate better fits.
But those values must be tested to determine whether
they are too high to reject the power law hypothesis.
The result of the hypothesis testing is shown in the
fifth column. In this case, the null hypothesis is that
the Kolmogorov distance is null, and the alternate hy-
pothesis is that the Kolmogorov distance is not null.
A null Kolmogorov distance implies that the distribu-
tion of the data is a power law. For a 99.99% sig-
nificance level (p = 0.01), all the programming lan-
guages except shell and Perl are fitted by a power law
(for sizes over the threshold shown in the third col-
umn, of course).
In short, for the case of shell and Perl files, the
high values tail is not a power law. For the rest of pro-
gramming languages, the high values tail is a power
law.
Regarding the parameters of the lognormal dis-
tribution, we use the standard maximum-likelihood
estimation routines included in the R statistical
package. In this case, the fitting procedure is more
straightforward, as we have already shown with the
quantile-quantile plot (Figure 3) that the data is very
Table 3: Parameters of the lognormal body for the top seven
programming languages and the overall sample.
Lang. ¯x s
x
D p
Overall 4.1262 1.4857 0.0436 0.0444
C 4.3421 1.5651 0.0448 0.0365
C++ 4.1182 1.2598 0.0363 0.1447
Shell 2.8480 1.3118 0.0656 0.0005
Java 3.7477 1.2627 0.0411 0.0697
Python 3.9543 1.3972 0.0416 0.0340
Perl 3.5272 0.9533 0.0700 ∼ 10
−16
Lisp 4.6485 1.3834 0.0381 0.1265
close to a lognormal, except for the tails. Table 3
shows the parameters of the lognormal distribution,
the Kolmogorov distance, and the results of the
hypothesis testing for the lognormal fitting. Again,
with a significance level of 99.99% (p = 0.01), for
small files, the size distribution of the programming
languages is lognormal—except for shell and Perl.
The distribution of size for all the program-
ming languages is a double Pareto, except for
the case of the shell and Perl programming
languages. This means that files can be di-
vided in two groups: small and large. The
frontier value between these two regions is
the threshold, x
min
, shown in Table 2.
5 SIZE ESTIMATION USING THE
LOGNORMAL AND DOUBLE
PARETO DISTRIBUTIONS
Software size can be estimated using the shape of the
distribution of source code file sizes, and knowing the
number of files that are going to be part of the sys-
tem. Size estimation can also be used for software
effort estimation. Analytical formulas for the case of
Java have even been proposed in the literature (Zhang
et al., 2009). Those formulas are based on the fact
that program size distribution is a lognormal, and use
the CCDF for the estimations.
For small files, the difference between a log-
normal or a double Pareto distribution is negligible.
However, for large files, this difference may be high.
This means that the proposed estimation models and
formulas can be very biased for large files.
Figure 5 compares the CCDF of the files written
in Lisp, with the double Pareto and lognormal esti-
mations of the CCDF. The threshold value is shown
with a vertical dashed line. For values higher than
the threshold, the lognormal model underestimates
ON THE DISTRIBUTION OF SOURCE CODE FILE SIZES
9

1 100 10000
1e−04 1e−02 1e+00
SLOC
P[X > x]
Data
Double Pareto
Lognormal
Figure 5: CCDF for the Lisp language, comparing the dou-
ble Pareto and lognormal models. Threshold value shown
as a vertical dashed line.
2e+03 5e+03 1e+04 2e+04 5e+04 1e+05
−100 −50 0 50 100
SLOC
RE
Lognormal
Double Pareto
Figure 6: Relative error in percentage for the CCDF of the
lognormal and double Pareto models, compared against the
CCDF of the sample. Only for files written in Lisp.
the size of the system, and this bias grows with the
size of file size – the bigger the file the more the bias.
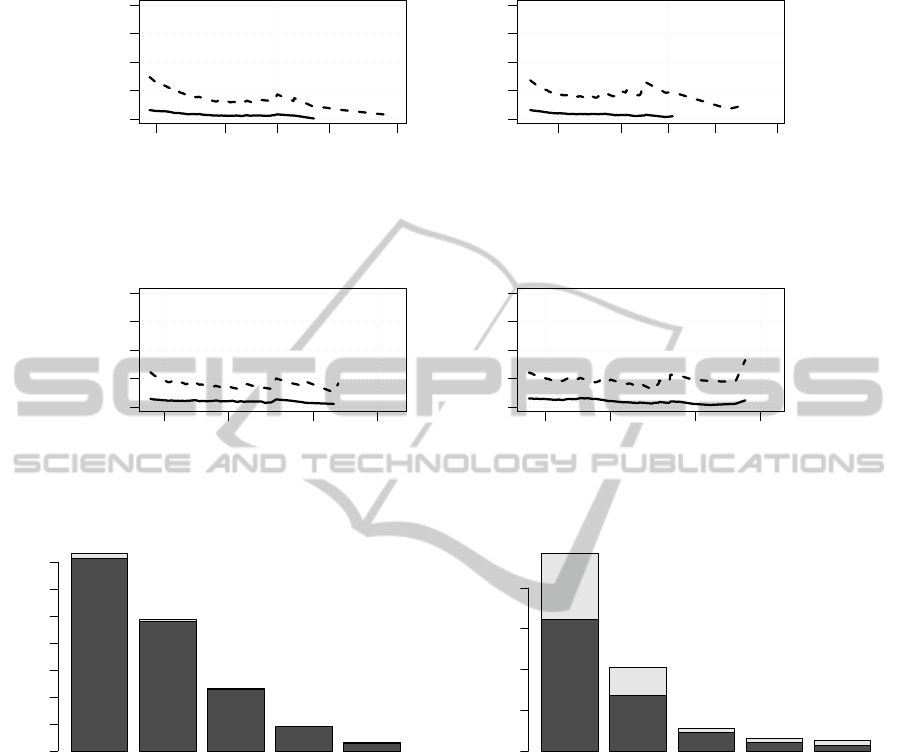
Figure 6 shows the relative error of the lognormal
and double Pareto models, for the case of the Lisp
language, when predicting the size of large files. The
CCDF of the fitted models were compared against the
CCDF of the actual sizes of the files. The lognormal
model always underestimates the size of files (nega-
tive relative error). The difference for large files is
so large that it cannot even be calculated because of
overflow errors.
The same pattern appears for the rest of program-
ming languages, as shown in Figure 7. The lognormal
model has a permanent bias that underestimate the
size of large. The reason is that files above a certain
threshold do not belong to that kind of distribution,
but to the power law tail of a double Pareto distribu-
tion.
Although large files are not as numerous (see
Figure 8), their contribution to the overall size is
as important as small files’ contribution. Figure 9
shows the relative importance of small and large
files for all the programming languages that have
been identified as double Pareto. The bottom part
(dark) of every column is the contribution of small
files, and the top part (clear) the contribution by
large files. Small files are those files with a size
lower than the threshold value shown in Table 2.
We do not include the Shell and Perl languages
because the distribution is not a double Pareto, and
therefore the threshold values do not make sense in
those cases. The plot clearly shows that the relative
contribution of large files is quite notable, even if
large files are only a minority. In other words, if
we compare Figures 8 and 9, even if the propor-
tion of large files is small, their relative contribution
to the overall size is much higher than that proportion.
Large files are only a minority. However,
they account for about 40% of the overall size
of the system. Therefore, an underestimation
of the size of large files will have a great im-
pact in the estimation of the overall size of
the system.
6 SUMMARY OF RESULTS
After measuring the size of almost 1.4 millions of
files, with more than 300 millions of SLOC in total,
we find that the statistical distribution of source
code file sizes is a double Pareto. Our findings hold
for five of the top seven programming languages in
our sample: C, C++, Java, Python and Lisp. The two
cases that do not exhibit this distribution are Shell and
Perl.
This finding is in conflict with previous stud-
ies (Zhang et al., 2009), which found that software
size’s distribution is a lognormal, and which pro-
posed software estimation models based on that find-
ing. We show how lognormal-based models dan-
gerously underestimate the size of large files.
Although the proportion of large files is very small
(e.g. less than 3% of the files in the case of C), their
relative contribution to the overall size of the system
is much higher (in the case of C, large files account for
more than 30% of the SLOC). Therefore, lognormal-
based estimation models are underestimating the
size of files that have the most impact in the overall
size of the system.
7 THREATS TO VALIDITY
The main threat to the validity of the results and con-
clusions of this paper is the metric used for the study.
SLOC is defined as lines of text, removing blanks and
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
10
2000 5000 10000 50000
−100 0 50
C
SLOC
RE
2000 5000 20000 50000
−100 0 50
C++
SLOC
RE
1000 2000 5000 10000
−100 0 50
Java
SLOC
RE
1000 2000 5000 10000
−100 0 50
Python
SLOC
RE
Figure 7: Relative error in percentage for the CCDF of the lognormal and double Pareto models, compared against the CCDF
of the sample, for C, C++, Java and Python.
C C++ Java Python Lisp
% Files
0 5 10 15 20 25 30 35
Figure 8: Proportion of large and small files. The top of
the bars (clear) shows the amount of files over the threshold
values, or large files. The bottom of the bar (dark) shows
the amount of small files.
comments. It is a measure of physical size, not logical
size. For instance, if a function call in C is spawned
over several lines, it will be counted as several SLOC;
with a logical size metric, it would count only as one.
Measuring logical size is not straightforward. It
depends on the programming language. Also, there
might not be consensus about how to count some
structures like variables declaration. Should variable
declarations be counted as a logical line? And if there
is an assignation together with the declaration, should
be counted as one or two?
Coding style influences SLOC measuring. If the
coding style of a developer is to write function calls in
one line, and other developer spawns them over sev-
C C++ Java Python Lisp
% SLOC
0 10 20 30 40
Figure 9: Relative contribution of small and large files to the
overall size, for each programming language, in percentage
of SLOC. The top part of the bars (clear) is the proportion of
size due to large files. The bottom (dark) is the proportion
of size due to small files
eral lines, the second developer would appear as more
productive for the same code.
The sample under study includes code originating
from many different software projects. Therefore the
different coding styles are balanced, and the net re-
sult is representative of the actual size of the files un-
der study. However, when comparing different lan-
guages, such balance may not occur. Think for in-
stance of Lisp. Lisp syntax is based on lists, that are
represented by parentheses. Everything in Lisp is a
list: function definitions, function calls, control struc-
tures, etc. This provokes an accumulation of paren-
theses at the end of code blocks. Sometimes, for clar-
ON THE DISTRIBUTION OF SOURCE CODE FILE SIZES
11

(defun (m x y z)
(cond
((and (> x z) (> y z))
(+ (* x x) (* y y))
)
((and (> x y) (> z y))
(+ (* x x) (* z z))
)
(t (+ (* y y) (* z z))
)
)
)
Figure 10: Sample of code written in Lisp. Note the accu-
mulation of parentheses at the end of the blocks, resulting
in additional SLOC.
ity purposes, this parentheses are indented alone in a
new line, to match the start column of the block. Fig-
ure 10 shows an example, that will account for two
extra SLOC because of the coding style with the end-
ing parentheses. This makes the code more readable.
However, this practice will make Lisp to appear with
larger files than other languages. In general, the cod-
ing style can over represent the size of some program-
ming languages, and this may affect the shape of the
distribution.
Another threat to the validity of the results is the
sample itself. We have exclusively selected open
source, coming from only one distribution. Although
the sample is very broad and large, and the only re-
quirement for a project to be included is to be open
source, the distribution practices when adding soft-
ware to the collection may suppose a bias in the
sample. This threat to the validity can be solved
by studying other samples coming from different
sources. It can easily be tested whether the distribu-
tion with these other sources is still a double Pareto,
and whether the parameters of the distributions for
the different programming languages are different to
the values here. We have not distinguished between
different domains of application either, this is to say,
we include software that belongs to the Linux kernel,
libraries, desktop applications, etc, under the same
sample. There might be differences in the typical size
of a file for different domains of applications. How-
ever, we believe that the size distribution remains re-
gardless the domain of application. This threat to the
validity can be addressed extending this study split-
ting the sample by domain of application.
Finally, some packages may contain automatically
generated code. We have not tried to remove gener-
ated code in this study. In a similar study (Herraiz
et al., 2007), the authors showed that the influence of
very large generated files in the overall size and in the
shape of the distribution was negligible for a similar
sample, so we believe that in this case it does not af-
fect the validity of the results.
8 FURTHER WORK
The size of the sample under study makes it possible
to estimate some statistical properties of the popula-
tion from where it was extracted. In particular, the
parameters of the distribution appear to be related to
the properties of the programming language. Those
parameters could be used for software management
purposes. In this section, we discuss and speculate
about some of the possible implications of those pa-
rameters, which is clearly a line of work that deserves
further research.
The first interesting point about the distribution of
file sizes is the difference between the two regions,
lognormal and power-law, within that distribution.
One of the parameters of the distribution, x
min
, divides
the files among small and large files. But this is much
more than a label: small files belong to a lognormal
distribution and large files to a power law distribu-
tion. In other words, that threshold value separates
files that are of a different nature, small and large files
probably will exhibit different behavior in the main-
tenance and development processes. One explanation
could be that large files are not manageable by devel-
opers, so they either are split or abandoned. If they
are split, the original file will appear as one or more
small files. If they are abandoned, then instead of an
active maintenance process, they are probably subject
of only corrective maintenance.
This transition from the small to large file is un-
conscious, developers do not split files on purpose
when they get large. However, this unconscious pro-
cess is reflected as a statistical property of the system.
This means that the value of this transition point can
be used as a warning threshold for software mainte-
nance. If a file gets larger than the threshold, it is
likely that it will need splitting or it will become un-
manageable.
To verify these claims we need to obtain histori-
cal data about the life of files. We must obtain the
size of files after every change during their life, fol-
lowing possible renames. If we assume that files start
empty (or with very small sizes), with that historical
information we can find out how files grow over the
threshold size and change their nature. We can also
observe how the parameters of the distribution of size
changes over the history of the project. For instance,
the double Pareto distribution might be a character-
istic of only mature projects. Another point that de-
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
12

Table 4: Median and threshold sizes (in SLOC), and scaling
parameter for five programming languages.
Lang. Median x
min
α
C 85 1, 820 2.87
C++ 58 1, 258 2.80
Java 43 846 3.17
Python 59 826 2.90
Lisp 132 1, 270 2.73
serves further work is why shell and Perl do not ex-
hibit this behavior.
The parameters of the distribution seem to be re-
lated to the programming language. Table 4 summa-
rizes the median, threshold sizes and scaling param-
eters for the five languages with a double Pareto dis-
tribution. We use medians and not average values be-
cause the distribution of size is highly right skewed,
and very large files may easily distort the average
value; the median value is more robust to very large
files.
The higher thresholds correspond to C, C++ and
Lisp. These languages also have the highest median.
This is probably due to the expressiveness of the lan-
guage (in terms of number of required lines of code
per unit of functionality). C and Lisp are the least ex-
pressive languages. In C for instance, complex data
structures are not available by default in the language,
and they have to be implemented by the developer,
or reused from a library. In Lisp, because of its sim-
ple syntax, it probably requires more lines of code to
perform the same tasks that in other languages. The
median size of Lisp files seem to support this argu-
ment.
Java and Python have the lowest thresholds. The
case of Java is interesting because the median size of a
file in Java is much lower than in C++, in spite of the
similarity between the two programming languages.
This difference is also present in the threshold val-
ues. Again, the reason may be in the rich standard
libraries that accompany Java and that are not present
in C++. The same can be said if we compare C++ and
Python. These results are similar to the tables com-
paring function points and lines of code, that were
firstly reported by Jones (Jones, 1995); higher level
(and more expressive) languages have lower number
of lines of code per function point.
In short, these threshold values can be understood
as a measurement of the maximum amount of in-
formation that can be comprehended by a developer.
Above that threshold, programmers decide to split the
file, or just abandon it because it turns unmanageable.
The values are different for different programming
languages because the same task will require more or
less lines depending on the language, but they repre-
sent the same quantity or limit value. There are of
course other factors that can influence program com-
prehension (Woodfield et al., 1981), but all other fac-
tors being the same, we believe that these parameters
can be related to comprehension effort for different
programming languages.
The scaling parameter, α, is also related to the ex-
pressiveness. Its value is related to the slope of CCDF
in the large files side. Lower values of α will lead
to higher file sizes in that section. If we sort by its
value all the programming languages (see Table 4),
the most expressive language is Java, closely followed
by Python. The least expressive language is Lisp.
Lisp is a simple language in terms of syntax, and it
probably requires to write more lines of code than
in other languages to perform similar tasks. There-
fore, the scaling parameter can also be understood as
a measure of the expressiveness of the programming
language.
In short, the plan that we plan to explore as further
work are the following:
• Analysis of the evolution of files over time, to find
out how the threshold value is related to the evo-
lution of files.
• Extend the study to large samples of other pro-
gramming languages, and divide the analysis by
domain of application, to determine whether the
features of the language are related to the values
of the parameters of the double Pareto distribu-
tion, and whether different domains exhibit dif-
ferent behaviors.
• Why some languages do not show a double Pareto
distribution?. How the evolution of files of sys-
tems written in these languages differ from double
Pareto languages?
9 CONCLUSIONS
The distribution of software source code size follows
a double Pareto. We found the double pareto charac-
teristic to hold in five of the top seven programming
languages of Debian. The languages whose size fol-
lows a double Pareto are C, C++, Java, Python and
Lisp. However, Shell and Perl behave differently.
Shell and Perl are scripting languages. In the De-
bian GNU/Linux distribution, shell and Perl are pop-
ular languages for package maintenance. The pack-
age maintenance tasks are quite repetitive, and they
are probably the same for a broad range of different
packages. So it is probably not difficult to find scripts
as part of the packages to make the packaging pro-
cess easier. Scripts are different to other kind of pro-
ON THE DISTRIBUTION OF SOURCE CODE FILE SIZES
13

grams: they are probably less complex and smaller.
If the difference is due to this cause, it would mean
that double Pareto distributions are the signature of
the programming process, and that different program-
ming activities (scripting, complex programs coding)
can be identified by different statistical distributions
of software size.
In any case, the double Pareto distribution already
has important practical implications for software es-
timation. Previously proposed models (Zhang et al.,
2009) are based on the lognormal distribution, that
consistently and dangerously underestimate the size
of large files. It is true that large files are only a minor-
ity in software projects, the so-called small class/file
phenomenon, however they account for a proportion
of the size as important as in the case of small files.
Therefore, using the lognormal assumption leads to
an underestimation of the size of large files. This un-
derestimation will have a great impact on the accuracy
of the estimation of the size of the overall system.
REFERENCES
Baxter, G., Frean, M., Noble, J., Rickerby, M., Smith, H.,
Visser, M., Melton, H., and Tempero, E. (2006). Un-
derstanding the shape of java software. In Proceedings
of the ACM SIGPLAN Conference on Object-Oriented
Programming Systems, Languages, and Applications,
pages 397–412, New York, NY, USA. ACM.
Boehm, B. B. (1981). Software Engineering Economics.
Prentice Hall.
Clark, D. W. and Green, C. C. (1977). An empirical study
of list structure in Lisp. Communications of the ACM,
20(2):78–87.
Clauset, A., Shalizi, C. R., and Newman, M. E. J. (2007).
Power-law distributions in empirical data.
Concas, G., Marchesi, M., Pinna, S., and Serra, N. (2007).
Power-laws in a large object oriented software sys-
tem. IEEE Transactions on Software Engineering,
33(10):687–708.
Graves, T. L., Karr, A. F., Marron, J., and Siy, H. (2000).
Predicting fault incidence using software change his-
tory. IEEE Transactions on Software Engineering,
26(7):653–661.
Halstead, M. H. (1977). Elements of Software Science. El-
sevier, New York, USA.
Herraiz, I. (2009). A statistical examination of the evo-
lution and properties of libre software. In Proceed-
ings of the 25th IEEE International Conference on
Software Maintenance (ICSM), pages 439–442. IEEE
Computer Society.
Herraiz, I., Gonzalez-Barahona, J. M., and Robles, G.
(2007). Towards a theoretical model for software
growth. In International Workshop on Mining Soft-
ware Repositories, pages 21–30, Minneapolis, MN,
USA. IEEE Computer Society.
Jones, C. (1995). Backfiring: converting lines of code to
function points. Computer, 28(11):87 –88.
Knuth, D. E. (1971). An empirical study of FORTRAN pro-
grams. Software Practice and Experience, 1(2):105–
133.
Louridas, P., Spinellis, D., and Vlachos, V. (2008). Power
laws in software. ACM Transactions on Software En-
gineering and Methodology, 18(1).
McCabe, T. J. (1976). A complexity measure. IEEE Trans-
actions on Software Engineering, SE-2(4):308–320.
Mitzenmacher, M. (2004a). A brief history of generative
models for power law and lognormal distributions. In-
ternet Mathematics, 1(2):226–251.
Mitzenmacher, M. (2004b). Dynamic models for file sizes
and double Pareto distributions. Internet Mathemat-
ics, 1(3):305–333.
R Development Core Team (2009). R: A Language and
Environment for Statistical Computing. R Foundation
for Statistical Computing, Vienna, Austria. ISBN 3-
900051-07-0.
Robles, G., Gonzalez-Barahona, J. M., Michlmayr, M.,
Amor, J. J., and German, D. M. (2009). Macro-
level software evolution: A case study of a large soft-
ware compilation. Empirical Software Engineering,
14(3):262–285.
Robles, G., Gonzlez-Barahona, J. M., and Michlmayr, M.
(2005). Evolution of volunteer participation in libre
software projects: evidence from Debian. In Pro-
ceedings of the 1st International Conference on Open
Source Systems, pages 100–107, Genoa, Italy.
Woodfield, S. N., Dunsmore, H. E., and Shen, V. Y. (1981).
The effect of modularization and comments on pro-
gram comprehension. In Proceedings of the 5th inter-
national conference on Software engineering, ICSE
’81, pages 215–223, Piscataway, NJ, USA. IEEE
Press.
Zhang, H., Tan, H. B. K., and Marchesi, M. (2009). The
distribution of program sizes and its implications: An
Eclipse case study. In Proc. of the 1st International
Symposium on Emerging Trends in Software Metrics
(ETSW 2009).
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
14
