OPERATIONAL HAZARD RISK ASSESSMENT USING

BAYESIAN NETWORKS

Zoe Jing Yu Zhu, Yang Xiang

School of Computer Science, University of Guelph, Guelph, Canada

Edward McBean

School of Engineering, University of Guelph, Guelph, Canada

Keywords: Bayesian networks, Risk assessment, Pathogens, Reliability, Water treatment plants, Membranes, Ultra

filtration.

Abstract: This research investigates a method for hazard identification of modern drinking water treatment

technologies. Bayesian networks are applied to quantify risk assessment. Bayesian networks represent an

important formalism for representation of, and inference with, uncertain knowledge in artificial intelligence.

A physicochemical ultra filtration (UF) membrane train is expressed as a Bayesian network. They can be

used in quantifying understanding of the hazards at the operational level of treatment plant that impact the

risk of infection from pathogens. Once such a Bayesian network is established, the risk assessment can be

performed automatically using algorithms developed in artificial intelligence which facilitates risk

assessment of complex water treatment domains.

1 INTRODUCTION

Bayesian Networks, developed from the field of

artificial intelligence (AI), provide a powerful

knowledge representation formalism that deals with

uncertainty explicitly in a principled manner (Pearl,

1988). Over the last three decades, Bayesian

networks have been widely applied to many tasks

for reasoning under uncertainty (Jensen and Nielsen,

2007; Darwiche, 2009).

Effective operation of a water treatment system

must be able to handle uncertainty. Consider, for

example, an ultra filtration (UF) membrane train.

Water of varying pre-treated quality enters a

treatment facility and may produce varying qualities

of treated water. Failures of key pieces of

mechanical equipment or process may also influence

the quality of the treated water. In this work, we

investigate application of Bayesian networks to risk

assessment in complex water treatment domains.

2 BACKGROUND

2.1 Bayesian Networks

A Bayesian network consists of a directed acyclic

graph (DAG) and an associated joint probability

distribution (jpd). The nodes in the graph are

labelled by the set of random variables, N = {X

……X

). These random variables represent

alternative states. Each variable can be Boolean (two

possible values) or take one of more than two

possible values (Zhu et. al., 1998). For example, a

variable can denote the intensity of suspended solids

at a water treatment plant with possible values (low,

normal, or high). The links in the DAG specify the

causal relations among the random variables. Any

node X

in a Bayesian network is independent of any

non-descendent variable conditioned on its parent

nodes. That is, the parents of X

shield the variable

from the influence of all variables in the graph

except those downward from X

along the cause

direction. For example, suppose X

is the parent of

and X

is the child of X

: a direct path X

→ X

→

. If there is no other path from X

to X

, then X

135

Zhu Z., Xiang Y. and McBean E..

OPERATIONAL HAZARD RISK ASSESSMENT USING BAYESIAN NETWORKS.

DOI: 10.5220/0003430801350139

In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 135-139

ISBN: 978-989-8425-54-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

and X

are conditionally independent given X

The uncertain causal strength between a variable

and its parents π(X

) is quantified by a conditional

probability table P(X

| π(X

)). The dependence and

independence relations represented by the DAG

allow the joint probability distribution (jpd) over N

to be specified through conditional probability tables

of associated with nodes of the network. That is, the

jpd P(N) can then be written as:

∏

∈

XXPNP ))(|()(

(1)

Normally, the specification of a jpd requires the

specification of parameters in an order exponential

to the total number of variables. The major benefit

of using a Bayesian network representation is that

the jpd over a very large set of variables can be

compactly specified by a much smaller number of

variables, due to the above decomposition.

Once a model of an application domain, such as

a water treatment plant, is constructed in the form of

a Bayesian network. The Bayesian network can be

used to infer the value of some unobservable

variables given the observation of some other

variables, including prediction and explanation, two

basic tasks in monitoring and control (Sanguesa et

al., 2000). In this paper, we show that a

physicochemical ultrafiltration (UF) membrane train

can be expressed as Bayesian networks for

identifying faults and reducing the risk on potable

water delivery.

2.2 Cryptosporidium and Treatment

Options

In recent studies, waterborne outbreaks occurred

under conditions where water quality complies with

the standards on E. Coli and coliforms but water

treatment failed to eliminate high concentrations of a

persistent pathogen such as Cryptosporidium,

(Richardson et al., 1991). Protozoan parasites of the

genera Cryptosporidium and Giardia are important

causes of disease and morbidity in humans and of

losses in livestock production. Reducing the risk of

infection of cryptosporidium, and keeping the water

safe is one of the goals for the millennium (WHO,

2009). Ultrafiltration (UF) membrane train system,

as an alternative to conventional water treatment for

drinking water, has developed very fast due to their

ability for the removal of microbial pathogens,

especially Cryptosporidium and Giardia (Brehant et

al., 2010). The Ultrafiltrtion membrane system can

effectively block pathogens, virus, bacteria and is a

competitive option to produce high quality potable

water (Chelme-Ayala et al., 2009).

Membrane processes are new technologies. We

have limited information about this new system.

Given the complexity of water treatment plant

operations, a long time period is needed to observe

and reveal the characteristic of the system.

Beauchamp et al. (2010) apply fault tree analysis to

a physicochemical ultrafiltration membrane train,

with the objective of developing a systematic

approach for organizing and improving our

understanding of hazards at the treatment plant

operational level that affect the risk of infection

from the pathogen Cryptosporidium parvum. The

approach was successful in identifying many

technical and operational hazards. However,

quantification of probabilities of fault events is

incomplete. Such quantification can help to

prioritize interventions at the operational levels. In

this paper, we study the potential of applying

Bayesian networks to identify faults in the

membrane train system. We show that the

physicochemical or mechanical component of the

UF treatment train can be expressed as a Bayesian

network. Once the Bayesian network is established,

the risk assessment can be performed automatically

using the Bayesian network model.

3 THE FAULT TREE APPROACH

Figure 1 shows a simple fault tree. Pre-distribution

contamination is the top event (root event). Source

water contamination and treatment failure are

intermediate events. They are shown as boxes.

Circles, labelled source contamination, pathway

contamination, filtration failure and disinfection

failure represent basic events (leaf events).

Figure 1: A simple fault tree.

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

136

A fault tree is constructed to calculate the

probability of the top event. The structure of the

fault tree and the logic gates provide information on

how to perform the calculation. For an OR-gate with

n input events, if we know the probabilities P

(i=1,

2, ..., n) of input events, the probability P

of the

output event is computed as

Pr = 1-

)1(

∏

−

(2)

For an AND-gate with n input events, the

probability Pr of the output event is computed as

Pr =

∏

(3)

By combining Equations (2) and (3) according to

the fault tree topology, the probability of the root

event can be computed.

A fault tree may be considered detailed enough

when it corresponds to system analyzed with small

number of leaf variables and those variables can be

estimated. However, it is quite likely that in a

complex system, in order to calculate the multiple

root events, many possible leaf events might have to

be analyzed. Creation of multiple diagrams may

cause inconsistency and duplicated effort in both

specification and analysis. With leaf events isolated

in different diagram, it is not a simple matter to

consider their interactions. Therefore, combining

fault trees for multiple leaf events into one coherent

single interaction of multiple leaf events into one

coherent fashion as show in Figure 2 and Table 1.

The computation of root event probabilities,

however, will be handled in exactly the same

manner if the Bayesian network representation is

constructed. In this research, we show that Bayesian

network will offset the short comes from fault tree.

3.1 Fault Tree to an Ultrafiltration

Membrane

The process of a UF membrane train water treatment

plant consists of two major steps. The first step, pre-

treatment, includes screening, coagulation, static

mixing and mechanical flocculation. The objective

of pre-treatment is to condition the water for optimal

UF operation. Step2. Pre-treatment submerged UF

hollow fibre membrane trains, and chlorination.

Membrane filtration is a physical removal

process. Particles, pathogens and flocs are removed

by size. Fibre walls are made of a supporting

structure, which constitutes most of the thickness of

the fibre, and the active layer, a skin that rejects

particles and pathogens. UF membranes are an

absolute barrier to protozoan (oo)cysts and bacteria,

their absolute pore size of 0.1 µm being smaller than

the size of contaminants, which are greater than 3

µm for (oo)cysts and approximately 1µm for

bacteria. Membrane integrity testing (USEPA, 2005)

and monitoring are therefore critical for ensuring

that the membrane system is functioning as required.

Figure 2 and Table 1 represent a fault tree for UF

membrane train diagnosis. A water treatment plant

operation is a complex task where many factors

must be taken into account. The fault tree takes one

top event, high concentration of cryptosporidium

parvum in permeate. 14 intermediate events such as

the membrane skin is damaged and does not remove

pathogens and 19 basic events, such as membranes

are fouled.

Figure 2: Fault tree for UF membrane train diagnosis

(Modified from Beauchamp et. al., 2007).

In various works (Sanguesa, et. al., 2000,

Beauchamp et al. 2010; Zhu et., al., 1998), the

limitations of fault tree systems for monitoring,

control, and diagnosis applications are analyzed.

Fault trees only allow propagation of information

from leaf events towards the root event, but no

facility to explain observation of root event in terms

of most likely leaf events. Furthermore, each fault

tree typically can accommodate only one root event.

Multiple root events typically require multiple fault

trees, even though their leaf events may overlap.

Such duplication of leaf events may lead to

inconsistency as well duplication of resources (time,

space, and computation).

OPERATIONAL HAZARD RISK ASSESSMENT USING BAYESIAN NETWORKS

137

Table 1: The definition of fault tree in Figure 2.

Abbreviation Definition

AITIMS Air is trapped in the membrane system

APP Abrasive particles (silt, clay, silica, ) are

present

APRAM Abrasive particles rub against

membrane

AUIPBIO A unit is put back in operation

AWHO A water hammer occurs

BCABMS Bio-chemical agent breaches membrane

skin

CIL Coupling is loose

CIPCAS Changes in transmembrane pressure

causes an air shock

COPBW Components of the processes breaks in

the water

CSDBMS Chemical solution dose breaches

membrane skin

FBCMF Foreign body cuts membrane fibers

HCOCP High concentration of Cryptosporidium

parvum detected in the permeate

IAPRUL Internal air pressure reaches an

unbearable level during an integrity test

MAF Membranes are fouled

MB Membrane bursts

MC Membrane collapses

MISMID Membrane suffer manufactured or

installation defect

MMIS Membrane modules are improperly

stored

MSD(FRP) Membrane skin is damaged (fail to

remove pathogens)

MSOU Membrane skin is worn out

MVSLC Movement/vibration of the stem loosens

coupling

ODIMT Objects are dropped in the membrane

tank

OETFPS Objects enter the tank from pump

station

OGTPAS Objects go through pumps and screens

PITL Permeability is too low

PSBMS Particles/solids breach membrane skin

SDIB Screening device is breached

SIWO Seal is worn out

SOCF Seal or Coupling fails

SSMFD Seal Suffers from manufactured or

installation defect

TPRUL Transmembrane pressure reaches an

unbearable level

VCR Valve closes rapidly

WBNF(SC) Water bypass membrane filtration

(short-circuit)

WVITH Water viscosity is too high

One of the most important tasks for the application

of UF membrane systems is to monitor membrane

integrity during operation, detects and repairs the

defects because small defects could result in

significant reduction of pathogen removal efficiency

and consequently reduce UF membrane

performance. A secure and sound decision support

technique is the key to detect faulty membranes and

repair it immediately.

3.2 Bayesian Networks to a UF

Membrane

The major portion of the fault tree analysis is the

computation of probabilities for end events. It can be

readily expressed as a Bayesian network. The events

make the nodes in the network. The events that

cause a branching event are the direct parents of the

resultant event. The same set of probabilities that

used to specify a fault tree can be used to specify the

conditional probability distribution at each node of a

network. Once a fault tree is expressed as a Bayesian

network, the computation of end event can be

performed using expert system shells for

probabilistic reasoning in Bayesian networks. This

allows accurate and speedy analysis of a UF water

treatment system.

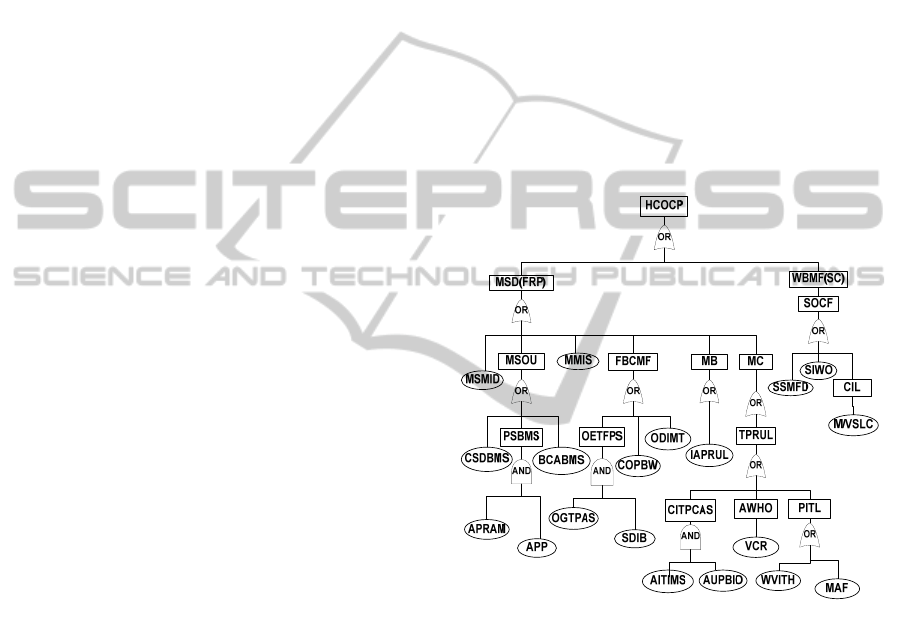
Figure 3 represents a UF membrane train water

treatment system as a Bayesian network. Our

illustration is aided with WebWeavr IV (Xiang,

2007) expert system shell. We use the variable

names defined in Table 1 to label the nodes in the

Bayesian network. We assume the probabilities of

the leaves are given or can be observed, for example,

water viscosity is too high, membranes are fouled,

etc., and other variables probability can be computed

by the shell when the Bayesian network is specified.

The probability of the top event, high concentrations

of cryptosporidium parvum (HCOCP) detected in

the permeate will be computed efficiently. If we

observed the HCOCP, we also can detect and trace

which variable caused the HCOCP.

Figure 3: Bayesian network for UF membrane train

diagnosis.

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

138

The advantage of Bayesian networks over fault

trees can be understood in relation to the limitations

of fault trees mentioned earlier. For instance, with a

Bayesian network, not only the probability of root

fault can be computed based on probabilities of leaf

events, but also when the root fault is observed, the

most likely causing leaf events can be computed. A

Bayesian network can also simultaneously include

multiple variables each of which corresponds to the

root event of a fault tree. Each of the contributing

leaf events need to be represented exactly once,

which eliminates inconsistency and duplication of

resources. The probabilities of all root events thus

represented can be computed in one round of

inference propagation by working with a single

coherent model.

To summarize, using a Bayesian network

representation, the following can be achieved:

• Multiple fault trees can be consistently and

economically encoded into a single Bayesian

network,

• The probability of any non-leaf faulty tree

event can be computed using such a Bayesian

network, This function quantifies risk in the

same way as fault trees.

• The probability of any non-leaf faulty tree

event given some leaf events have occurred

can be computed. When the probability

obtained is 1, it signifies that these leaf events

definitely cause the non-leaf event. This

function can be used in a what-if analysis to

predict high-level faults given occurrence of

some low-level faults.

• The probability of any leaf event given that

some non-leaf events have occurred can be

computed. This function can be used to

facilitate investigation of causes when a high-

level fault has occurred.

4 CONCLUSIONS

In this paper, we have described how to represent a

fault tree through a UF membrane train as a

Bayesian network. We demonstrate the Bayesian

network can overcome the shortcomings of a fault

tree. Bayesian network can perform more efficiently

when there are multiple leaf events. The analysis

performed in a risk assessment using a Bayesian

network is a forward inference, i.e., probabilities for

the leaves events are given, the probabilities for top

events are to be computed. The Bayesian network

can also be used as backward inference. If we

observed top event, we can diagnose which

operation is the most likely cause. If high

concentrations of Cryptosporidium parvum are

detected in the permeate, we can find possible

causes rapidly to reduce the adverse consequence.

Bayesian network also allows the interaction

between any variables in the Bayesian network and

update the information which provides the dynamic

behaviour of the system. The probabilistic approach

enables uncertainty analysis and calculations of

probability of exceeding defined performance targets

and acceptable levels of risk. It makes Bayesian

network an important method in decision support.

REFERENCES

Aloy, M., and Vulliermet, B., 1998. Membrane

technologies for the treatment of tannery residual

floats, J. Soc. Leather Technol. Chem. Chem., 82, 140-

142.

Castro-Hermida, J.A., Garcia-Presedo, I., Gonzalez-

Warleta, M., Mezo, M., 2010. “Cryptosporidium and

Giardia detection in water bodies of Galicia, Spain”,

Water research 44, 5887-5896.

Beauchamp, N., Barbara, J. L., and Bouchard, C., 2010.

“Technical hazard identification in water treatment

using fault tree analysis”, Can.J. Civ. Eng. 37(6):897-

906.

Charniak, E., 1991. "Bayesian networks without tears", AI

Magazine, 12(4):50-63.

Chelme-Ayala, P., Smith, D. W.; El-Din, M. G., 2009.

“Membrane concentrate management options: a

comprehensive critical review” Can. J. Civ. Eng. Vol.

36.

Jensen, F. V. and Nielsen, T., D., 2007. “Bayesian

Networks and Decision Graphs (second edition)”,

Springer Verlag.

Peal, J., 1988. “Probabilistic reasoning in intelligent

systems”, 2nd. ed., San Francisco, Calif., Morgan

Kaufmann.

Richardson, A. J., Frankenberg, R. A., Buck, A. C.,

Selkon, J. B., Colbourne, J. S., Parsons, J. W., Mayon-

White, R.T., 1991. “An outbreak of waterborne

cryptosporidiosis in Swindon and Oxfordshire.

Epidemiol”. Infext. 107 (3), 485-495.

Sanguesa, R., Burrell, P., 2000. “Application of Bayesian

network learning methods to waste water treatment

plants”, Applied Intelligence 13, 19-40.

WHO (World Health Organization), 2009. Heath and the

millennium development goals. Available at.

Http://www.who.int/mdg/en.

Xiang, Y., 2007. “Probabilistic Reasoning in Multi agent

Systems”, Cambridge University Press, UK.

Zhu, J. Y., Cooke, W., Xiang, Y., and Chen, M., 1998.

“Application of Bayesian networks to quantified risk

assessment‟, Proc. 5th Inter. Conf. on Industrial

Engineering and Management Science, 321-328.

USEPA, 2005. “Membrane Filtration Guidance Manual,

Office of Water”.

OPERATIONAL HAZARD RISK ASSESSMENT USING BAYESIAN NETWORKS

139