A STUDY FOR MANUFACTURING CELL FORMATION

APPROACH CONSIDERING SETUP

Arthur Tórgo Gómez, Cristiano Galafassi

Universidade do Vale do Rio dos Sinos, Av. Unisinos - 950, São Leopoldo, Brazil

Iris Corrêa das Chagas Linck

Universidade do Vale do Rio dos Sinos, Av. Unisinos - 950, São Leopoldo, Brazil

Toni Ismael Wickert

Universidade do Vale do Rio dos Sinos, Av. Unisinos - 950, São Leopoldo, Brazil

Keywords: Manufacturing cell formation, Setup, Meta-heuristic, Tabu search, Genetic algorithm.

Abstract: This paper proposes a comparison among the exact methods Rank Ordered Cluster, Single Linkage

Clustering and the metaheuristics Tabu Search and Genetic Algorithm for Manufacturing Cell Formation

Problem. The Manufacturing Cell Formation consists of group machines for processing similar parts or

components in order to minimize setup time. Setup time can be defined as the period of downtime between

the processing of two consecutive batches. To validate the algorithms results, a metric, group efficacy, is

applied to determine the result quality, moreover, the results are compared with examples in the literature.

1 INTRODUCTION

Nowadays, customers increasingly want

personalized products, which forces suppliers to

produce a wide variety of products in smaller

amounts. In this context, the Group Technology

(GT) provides an important contribution in

managing the conflict between productivity and

flexibility in a production line (James et. al., 2007;

Papaioannou et al., 2008). The GT is a philosophy of

manufacturing in which parts are identified and

grouped according to some similarity in design or

manufacturing, called Parts Families (PFs) (James et

al, 2007).

The Manufacturing Cell Formation Problem

(MCFP) consists in determining how the machines

should be grouped (James et. al., 2007). The set of

parts with similar processing needs to be completely

manufactured in the same cell.

This paper approaches the manufacturing cell

formation problem using four algorithms: ROC,

SLC, the meta-heuristics Genetic Algorithm and

Tabu Search. To make the comparison between the

quality of the Manufacturing Cells (MC) generated

by each algorithm is used the grouping effectiveness

metric, proposed by Kumar and Chandrasekharan

(1990) and also applied by James et al. (2007).

This paper is divided as follows. Section 2

presents the basic concepts about the manufacturing

cells formation problem and the metrics that will be

used to evaluate the efficiency of the groups that will

be generated. Section 3 presents the techniques that

will be used to generate clusters. Section 4 describes

the model proposed in this paper. Section 5 presents

the results obtained from the experiments and

Section 6 presents the conclusions.

2 MANUFACTURING CELL

FORMATION PROBLEM

The Manufacturing Cell can be characterized as a

grouping of two or more machines which can

manufacture a parts family with little or no

intercellular movement (James et. al., 2007),

providing benefits such as reduced costs with

Tórgo Gómez A., Galafassi C., Corrêa das Chagas Linck I. and Ismael Wickert T..

A STUDY FOR MANUFACTURING CELL FORMATION APPROACH CONSIDERING SETUP.

DOI: 10.5220/0003439200430048

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 43-48

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

movement of materials and setup stops. The MCFP

is considered NP - hard (James et al., 2007;

Spiliopoulos and Sofianopoulou, 2008).

To solve this problem different methods have

been proposed like, exact methods (King, 1980;

King and Nakornchai, 1982; Kusiak and Chow,

1987), heuristics (Chan et al., 2002), metaheuristics

(Dimopoulos and Mort, 2001; Bajestani et al., 2009),

neural networks (Saidi-Mehrabad and Safaei, 2007)

and fuzzy theories (Safaei et al., 2008; Papaioannou

et al. 2008).

The MCFP can be formulated as a problem of

diagonalizing blocks which aims to group the largest

number of shares in the same cell, considering the

limited size of the magazine, where the matrix A =

] is defined by: a

= 1 if the j

component visits

the i

machine and a

= 0 otherwise (King, 1980).

Figure 1 illustrates an incidence matrix.

Figure 1: Incidence Matrix.

Figure 2 shows the result obtained after applying

the Cluster Identification Algorithm (Kusiak and

Chow, 1987).

Figure 2: Incidence Matrix after processing by CIA.

In Figure 2, we can see that two MC were

generated; MC1 with machines 5 and 3 and cell 2

with machines 4, 2 and 1. The asterisk (*) indicates

the parts 2 and 5 which need the MC 1 and 2 to be

processed. This resource sharing can be interpreted

as exceptional elements (King, 1980). In the

formulation of Parts Families, the bottlenecks can be

represented by machines that are claimed by two or

more Parts Families or by parts that must be

processed in two or more manufacturing cells.

To quantify the efficiency of the generated

clusters, several metrics have been proposed (Sarker,

2001). In the literature, there are two measures

frequently used to evaluate the quality of solutions.

The first one is called grouping efficiency that was

proposed by Chandrasekharan and Rajagopolan

(1989) and given by equation (1).

n = qn

+ (1

–

q) n

(1)

As such, q is the weighting factor, n

is the

relationship between the number of 1s in the

diagonal blocks and the total number of 0s and 1s on

the diagonal blocks, n

is the ratio between the

number of 0s outside the diagonal blocks and the

total number of 0s and 1s outside the diagonal

blocks (Chandrasekharan and Rajagopolan, 1989).

Grouping efficiency ranges from 0 to 1 and the

higher it is, the better the solution. As the q factor is

increased, an important relationship between the use

of machines and intercellular movement can be

obtained, but this metric has a low discriminatory

power as the array size increases (Sarker, 2001;

James et. al., 2007).

Kumar and Chandrasekharan (1990) proposed a

metric called effective clustering that overcomes the

matrix size problem (Sarker, 2001). This metric is

given by the equation (2).

vee

−

(2)

In this equation, e is the total number of 1s in the

incidence matrix, e

is the number of 0s in the blocks

diagonal and e

is the number of exceptional items.

3 METHODS TO SOLVE THE

MANUFACTURING CELL

FORMATION PROBLEM

Below it is presented the methods that will be

implemented to generate the Parts Families.

3.1 Rank Order Clustering

The Rank Order Clustering (ROC) was proposed by

King (King, 1980), this algorithm aims to calculate

the weight of each row and each column in the

incidence matrix and to reorder the incidence matrix

as these values.

Considering n = number of parts, m = number of

machines and a variable k, the weights for each row i

and column j are calculated by the equations 3 and 4

respectively.

Row i =

∑

−

(3)

Column j =

−

∑

(4)

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

The equation (3) defines the calculation used to

find the total weight of each line. The equation (4)

means calculation used to find the total weight of

each column. After applying ROC to the incidence

matrices, the Cluster Identification Algorithm

(Kusiak and Chow, 1987) was applied in order to

identify the clusters so that the metrics calculation

could be possible.

3.2 Single Linkage Clustering

The Single Linkage Clustering (SLC) is a

hierarchical method for the formation of MC. The

similarity coefficient between the parts is calculated

using the Jaccard Similarity Coefficient (JSC) giving

JSC

= (5)

Where JSC

is the Jaccard Similarity Coefficient

between j and k. N

is the number of machines that

the component j and k have in common in their

manufacturing and N

is the number of machines

that the component j must be manufactured. In this

case, the number of Parts Families is directly linked

to the similarity coefficient, limiting the space

search process.

3.3 Genetic Algorithm

The expression Genetic Algorithm (GA) was

presented by Holland (1975) and consists of a

heuristic method that simulates the evolutionary

process of natural selection and survival of the fittest

(James et al., 2007). Genetic algorithm has been

applied in a number of fields; e.g.: mathematics,

engineering, biology, and social science (Reeves,

2003).

The majority of the studies applying GA to the

MCFP use an integer code to represent solutions.

The objective function (OF), also known as

evaluation function or fitness, has the goal of

evaluating the actual solution quality. In the GA

case, each chromosome or individual represents a

solution, therefore, the OF calculation is done for

each chromosome. The objective function used in

this paper consists of the evaluation of the clustering

efficiency given by the equation below.

Minimize Z = (6)

Where:

= sum of the number of exceptional parts;

K= number of individual’s cells and it is defined

by GA as a random integer variable chosen in the

interval [2, m/2], being m the total number of matrix

tools.

The metric given by equation (6) will be applied

to the set of solutions generated by the GA.

3.4 Tabu Search

The heuristic method Tabu Search (TS) was

originally proposed by Glover in 1986 (Glover,

1986) for various combinatorial optimization

problems. The main ideas of TS are to avoid

recently visited area of the solution space and to

guide the search towards new and promising areas

(Glover, 1986). Non-improving moves are allowed

to escape from the local optima, and attributes of

recently performed moves are stored in a tabu list

and may be forbidden for a number of iterations to

avoid cycling (Glover, 1986).

The initial solution is obtained by a random

method, which draws random values for the clusters

of machines and parts. The neighbourhood structure

consists of two movements. The first movement

remove a machine or part from its cluster and inserts

it in another, since in the removed cluster remains, at

least, one machine or part. The second movement

swaps two machines or parts from different clusters.

A list of the five best solutions found is stored in a

candidate list. The intensification is applied every 20

consecutive iterations without improvement and

consists of taking the best solution of the candidate

list and generating a larger number of neighbours,

providing a robust search in a promising area. Every

time a candidate solution is used, it’s removed from

the candidate list. The tabu list applied in this paper

stores the machine or part moved and its origin

cluster for 20 iterations. Even so, a tabu movement

can be used since the objective function is improved.

The objective function used to evaluate the solutions

is the group efficacy, shown in section 2. The

stopping criterion applied is the maximum iteration

number without improvement (nbmax) and its size is

200.

4 ARCHITECTURE

To demonstrate the performance of each

implemented algorithm in the MCFP, we generated

300 random incidence matrices with a uniform

distribution. 100 instances size 10 x 10 and

magazine size limited to 4 tools, 100 instances size

40 x 20 and magazine size limited to 6 tools, and 50

instances size 100 x 100 and magazine size limited

to 6 tools. The magazine limitation means that a Part

NjkNkkNjj

Njk

−+

∑

KPj

A STUDY FOR MANUFACTURING CELL FORMATION APPROACH CONSIDERING SETUP

will not have more tools than its limitations.

The tests occur in two phases. In the first phase it

will be used two exact methods, ROC and SLC, and

two metaheuristics, TS and GA, to test their group

efficacy in random matrices. The second phase will

compare the group efficacy of the 4 techniques in a

set of 35 problems found in literature. Finally, the

results of GA and TS will be compared with the best

result found with the source problems. The tests

were run on a personal computer with a Core 2 Duo

processor and 2 GB of RAM Memory. Figure 3

shows the model architecture.

In this model, it can be observed that the ROC

obtains the solutions by the diagonalizing of the

matrices and the SLC obtains the solutions by the

similarity coefficient. These two techniques do not

see the problem as a whole at every stage of their

solution procedures. However, TS and GA consider,

for each solution, the whole problem of obtaining

better solutions. In the TS solutions are evaluated

using group effectiveness, maximizing the number

of 1s in the diagonal blocks, while in GA the fitness

function tries to reduce the exceptional items.

Figure 3: Model architecture.

5 COMPUTACIONAL

EXPERIMENTS AND RESULTS

Initially, the ROC, SLC, GA and TS were applied in

3 types of matrices, 10x10, 20x40 and 100x100. The

Table 1 below shows the matrices size and for each

technique, ROC, SLC, GA and TS, shows the group

efficacy presented in section 2, and its standard

deviation.

Table 1: Random matrices analysis.

Size ROC

SLC

GA δ TS δ

10x10 20,21

3,50

24,36

4,44

37,10

4,87 54,37 5,68

20x40 13,98

0,99

25,00

1,74 26,88 7,65 38,69 8,27

100x100 25,81

0,29

22,73

0,79

26,89

27,69

33,95 13,55

The group efficacy of the 4 techniques studied in

this paper was compared with a set of 35 problems

from the literature. These problems were presented

in James et. al. (2007) and the results were obtained

directly from the original article they appeared.

The Table 2 below presents an ID to identify the

problem, the source problem and the group efficacy

obtained using ROC and SLC. The values shown by

the GA and TS are the average group efficacy, they

are obtained in 100 executions of each matrix, and

their standard deviation.

Table 2: Comparing studied techniques.

ID Problem source ROC SLC

GA TS

Av.

King and

Nakornchai

(1982)

82,35 30,00 82,35 0,00 82,35 0,00

Waghodekar and

Sahu (1984)

57,14 50,00 49,79 6,74 69,57 0,00

Seifoddini

(1989)

85,19 40,74 77,36 0,00 79,59 0,00

Kusiak and

Chow (1992)

45,83 28,21 70,13 7,86 76,92 0,00

Kusiak and

Chow (1987)

36,51 32,43 42,85 2,47 60,87 0,00

6 Boctor (1991) 27,27 25,00 45,08 1,53 70,83 0,00

Seifoddini and

Wolfe (1986)

36,46 31,11 45,34 5,88 69,44 0,00

Chandrasekharan

and Rajagopalan

(1986a)

38,13 30,60 49,60 9,69 85,25 0,00

Chandrasekharan

and Rajagopalan

(1986b)

56,88 38,02 40,96 6,17 56,70 7,15

Mosier and

Taube (1985)

70,59 34,29 39,41 5,72 70,35 5,34

Chan and Milner

(1982)

92,00 29,21 48,31 7,70 92,00 0,00

Askin and

Subramanian

(1987)

61,46 23,15 25,62 4,98 55,35 6,78

13 Stanfel (1985) 55,45 16,95 26,00 4,32 68,71 3,94

McCormick et

al. (1972)

26,88 18,45 23,75 2,62 52,75 1,55

Srinivasan et al.

(1990)

32,07 21,43 24,43 5,35 53,74 6,57

16 King (1980) 28,25 19,23 20,83 2,06 55,78 1,24

17 Carrie (1973) 34,52 17,02 21,80 2,00 51,35 2,12

Mosier and

Taube(1985)

38,54 15,20 22,69 4,36 38,12 8,61

Kumar et al.

(1986)

32,65 14,84 21,23 3,36 50,13 2,10

20 Carrie (1980) 85,00 18,53 22,80 3,58 70,19 4,87

Boe and Cheng

(1991)

24,52 17,62 21,91 2,99 54,95 7,83

Chandrasekharan

and Rajagopalan

(1989)

98,50 13,42 17,68 3,11 100,00 0,00

Chandrasekharan

and Rajagopalan

(1989)

24,53 14,34 16,23 2,91 85,11 0,00

Chandrasekharan

and Rajagopalan

(1989)

14,75 13,64 15,58 1,64 73,51 0,00

Chandrasekharan

and Rajagopalan

(1989)

14,04 17,99 14,86 1,21 53,15 1,06

Chandrasekharan

and Rajagopala

(1989)

15,93 17,71 15,33 1,08 48,55 0,00

McCormicket

(1972)

35,59 16,10 21,97 3,82 53,41 3,91

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

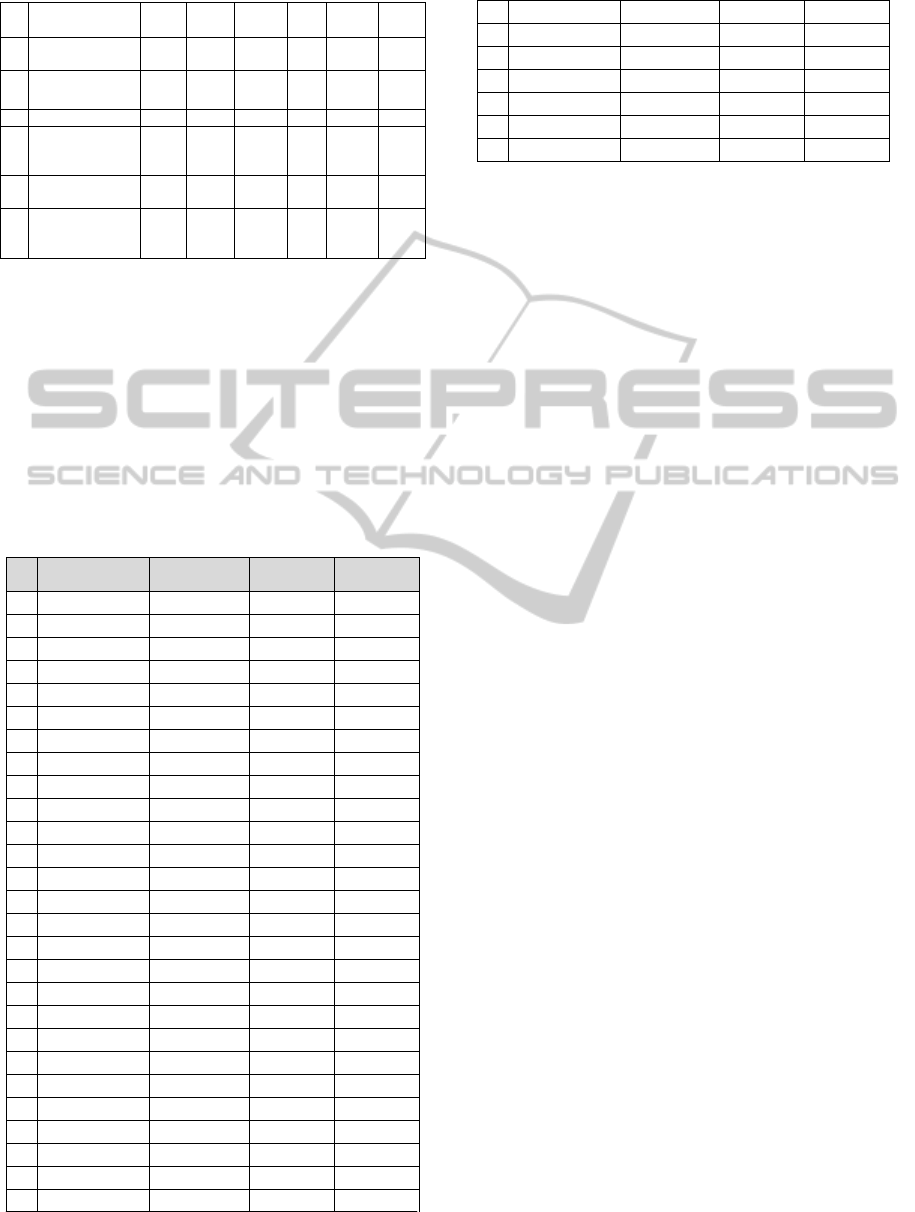
Table 2: Comparing studied techniques (Cont.).

29 Carrie (1980) 17,29 15,59 16,97 1,57 45,66 1,98

Kumar and

Vannelli (1987)

16,71 15,84 44,37 5,86 60,37 4,79

31 Stanfel (1985) 38,50 15,79 11,29 1,36 39,55 13,56

32 Stanfel (1985) 12,42 13,62 12,31 1,40 41,16 10,89

King and

Nakornchai

(1982)

13,87 12,74

9,59 1,53 43,19 3,89

McCormick et

al. (1972)

50,33 29,37

31,60 8,35 57,67 7,99

Chandrasekharan

and Rajagopalan

(1987)

27,42 10,01

12,01 1,30 83,08 0,91

In Table 2 above it can be observed that in this

set of 35 problems, ROC obtained the best solution

for the problems 1, 3 and 20, for all the other

problems, TS obtained the best average solution.

Finally, the techniques and the results found with

the source problem were compiled and analyzed.

Table 3 below shows the ID to identify the problem,

the technique which obtained the best solution in the

source problem articles and the best solutions

obtained by GA and TS.

Table 3: Comparing GA and TS with literature.

Resolution

Techniques

Best Solution

Found

Best GA Best TS

1 ZODIAC 73,68

82,35

2 GATSP 68,00

62,50

69,57

3 EA 79,59

77,36

79,59

4 GATSP 76,92

76,92

5 EA 53,13

46,51

60,87

6 GATSP 70,37

46,34

70,83

7 ZODIAC 68,30

53,70

69,44

8 EA 85,25

60,23

85,25

9 MST 58,72

56,07

58,72

10 GAL 72,79

46,15

75,00

11 ZODIAC 92,00

57,50

92,00

12 EA 69,86

32,76

69,86

13 GP 71,80

35,47

71,83

14 EA 52,58

28,24

52,75

15 ZODIAC 67,83

36,33

68,99

16 GAL 86,25

26,55

57,53

17 EA 54,46

26,24

57,43

18 EA 42,94

31,78

42,74

19 EA 49,65

29,03

50,81

20 GP 76,70

22,80

77,91

21 EA 58,07

21,91

57,98

23 MST 85,11

24,49

85,11

24 GRAFICS 73,51

20,33

73,51

25 GP 53,30

18,18

53,15

26 GP 47,90

19,05

48,55

27 EA 44,75

18,05

46,90

EA 54,27

31,36

53,41

Table 3: Comparing GA and TS with literature (Cont.).

29 EA 44,37

20,53

46,78

30 GP 60,70

54,98

62,24

31 GP 59,40

16,16

59,77

32 EA 50,48

16,89

50,83

33 EA 42,12

12,25

44,61

34 MST 56,42

46,38

60,48

35 GATSP 84,03

16,21

84,00

The ZODIAC was obtained from

Chandrasekharan and Rajagopalan (1987),

GRAFICS was obtained from Srinivasan and

Narendran (1991), GA-Genetic Algorithm was

obtained from Onwubolu and Mutingi (2001), GP-

Genetic Programming Algorithm was obtained from

Dimopoulos and Mort (2001). The results for

ZODIAC and GRAPHICS were both obtained from

Srinivasan and Narendran (1991); otherwise the

results were taken from the original citation.

6 CONCLUSIONS

This work presents a study for manufacturing cell

formation approach considering setup with the

application and analysis of 4 techniques, ROC, SLC,

GA and TS in random matrices with different sizes

and in a set of 35 known problems. Considering the

experiments universe, SLC obtained better solutions

in matrices size 10x10 and 20x40, in matrices size

100x100 ROC obtained better solution with a lower

standard deviation.

The TS and GA obtained better solutions and a

lower standard deviation compared with ROC and

SLC. It happened because TS and GA use the search

space to look for new solutions while ROC are

limited by the sorting technique and SLC are limited

by the similarity coefficient. Analysing the

techniques, in the set of 35 problems, it can be seen

that TS obtained better solutions in about 57% of the

35 problems studied while ROC obtained better

solutions in 8% of the 35 problems. Even so, TS

proved to be robust obtaining better solutions with a

low standard deviation. Finally, using a technique

that generates a better group efficacy means that

lower number of setups and lower setup time will be

needed to process a whole Parts Family, providing a

higher production rate.

REFERENCES

Askin, R. G., Subramanian, S. P., 1987. A cost-based

heuristic for group technology configuration.

A STUDY FOR MANUFACTURING CELL FORMATION APPROACH CONSIDERING SETUP

International Journal of Production Research, v. 25(1),

p. 101–13.

Bajestani, M. A., Rabbani M., Rahimi-Vahed, A. R. and

Khoshkhou, G. B., 2009. A multi-objective scatter

search for a dynamic cell formation problem,

Computers and Operations Research, 36, 777-794.

Boe, W. J., Cheng, C. H., 1991. A close neighbour

algorithm for designing cellular manufacturing

systems. International Journal of Production Research,

v. 29(10), p. 2097–116.

Chan, H. M., Milner, D.A., 1982. Direct clustering

algorithm for group formation in cellular

manufacture. Journal of Manufacturing Systems, v. 1,

p. 65–75.

Chan, W. M., Chan, C. Y. and Ip, W. H., 2002. A heuristic

algorithm for machine assignment in cellular layout,

Computers and Industrial Engeneering, 44, 49-73.

Chandrasekharan, M. P., Rajagopalan, R., 1986a.

MODROC: an extension of rank order clustering for

group technology. International Journal of Production

Research, v. 24(5), p. 1221–64.

Chandrasekharan, M. P., Rajagopalan, R., 1986b. An ideal

seed non-hierarchical clustering algorithm for cellular

manufacturing.International Journal of Production

Research, v. 24(2), p. 451–64.

Chandrasekharan, M. P., Rajagopalan, R., 1987. ZODIAC:

an algorithm for concurrent formation of part-families

and machine-cells.International Journal of Production

Research, v. 25(6), p. 835–50.

Chandrasekharan, M. P., & Rajagopalan, R., 1989. Group

ability: Analysis of the properties of binary data

matrices for group technology. International Journal of

Production Research, 27(6),1035–1052.

Dimopoulos, C., Mort, N., 2001. A hierarchical clustering

methodology based on genetic programming for the

solution of simple cell-formation problems.

International Journal of Production Research, v. 39, p.

1–19.

Glover, F., 1986. Future paths for integer programming

and links to artificial intelligence. Computers and

Operations Research, 1, p. 533-549.

Holland, J. H., 1975. Adaptation in natural and artificial

systems. Ann Arbor. MI: University of Michigan

Press.

James, T. L., Brown, E. C. and Keeling, K. B., 2007. A

hybrid grouping genetic algorithm for the cell

formation problem. Computers and Operations

Research, 34, 2059-2079.

King, J. R., 1980. Machine-component grouping in

production flow analysis: an approach using a rank

order clustering algorithm. International Journal of

Production Research, v. 18, p. 213–32.

King, J. R., Nakornchai, V., 1982. Machine-component

group formation in group technology: review and

extension. International Journal of Production

Research, v. 20(2), p. 117–33.

Kumar, K. R., Kusiak, A., Vannelli, A., 1986. Grouping of

parts and components in flexible manufacturing

systems. European Journal of Operations Research, v.

24, p. 387–97.

Kumar,

K. R., Vannelli, A., 1987. Strategic subcon-

tracting for efficient disaggregated manufacturing.

International Journal of Production Research, v.

25(12), p. 1715–28.

Kumar, K. R., & Chandrasekharan, M. P., 1990. Grouping

efﬁcacy: A quantitative criterion for goodness of block

diagonal forms of binary matrices in group

technology. International Journal of Production

Research, 28(2), 233–243.

Kusiak, A., Chow, M., 1992. Similarity coefficient

algorithm for solving the group technology problem.

International Journal of Production Research, v.

30(11), p. 2633–46.

Kusiak, A., Chow, W. S., 1987. Efficient solving of the

group technology problem. Journal of Manufacturing

Systems, v. 6(2), p. 117–24.

McCormick, W., Schweitzer, P., White, T., 1972. Problem

decomposition and data reorganization using a

clustering technique. Operations Research, v. 20, p.

993–1009.

Mosier, C. T., Taube, L., 1985. The facets of group

technology and their impact on implementation.

OMEGA, v. 13(5), p. 381–91.

Onwubolu, G. C., Mutingi, M., 2001. A genetic algorithm

approach to cellular manufacturing systems.

Computers & Industrial Engineering, v. 39, p. 125–44.

Papaioannou, G. and Wilson, J. M., 2008. Fuzzy

extensions to Integer Programming models of cell-

formation problems in machine scheduling. Annals of

Operations Research, 166, 163-182.

Saidi-Mehrabad, M. and Safaei, N., 2007. A new model of

dynamic cell formation by a neural approach,

International Journal of Advanced Manufacturing

Technology, 33, 1001-1009.

Safaei, N., Saidi-Mehrabad, M., Tavakkoli-Moghaddam,

R. and Sassani, F., 2008. A fuzzy programming

approach for a cell formation problem with dynamic

and uncertain conditions. Fuzzy Sets and Systems,

159, 215-236.

Sarker, B. R., 2001. Measures of grouping efficiency in

cellular manufacturing systems. European Journal of

Operational Research, 130(3),588–611.

Seifoddini, H., & Wolfe, P. M., 1986. Application of the

similarity coeffcient method in group technology. IIE

Transactions, 18, 3, 266-270.

Seifoddini, H., 1989. A note on the similarity coefficient

method and the problem of improper machine

assignment in group technology applications.

International Journal of Production Research, v. 27(7),

p. 1161–5.

Srinivasan, G, Narendran, T., 1991. GRAPHICS—a non-

hierarchical clustering algorithm for group

technology. International Journal of Production

Research, v. 29, p. 463–78.

Spiliopoulos, K.; Sofianopoulou S., 2008. An efficient ant

colony optimization system for the manufacturing cells

formation problem, International Journal of Advanced

Manufacturing Technology, 36, 589-597.

Waghodekar, P. H., Sahu, S., 1984. Machine-component

cell formation in group technology MACE.

International Journal of Production Research, v. 22, p.

937–48.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics