
RANDOM BUILDING BLOCK OPERATOR FOR GENETIC
ALGORITHMS
Ghodrat Moghadampour
VAMK, University of Applied Sciences, Technology and Communication, Wolffintie 30, 65200, Vaasa, Finland
Keywords: Evolutionary algorithm, Genetic algorithm, Function optimization, Mutation operator, Multipoint mutation
operator, Random building block operator, Fitness evaluation and analysis.
Abstract: Genetic algorithms work on randomly generated populations, which are refined toward the desired optima.
The refinement process is carried out mainly by genetic operators. Most typical genetic operators are
crossover and mutation. However, experience has proved that these operators in their classical form are not
capable of refining the population efficiently enough. Moreover, due to lack of sufficient variation in the
p
opulation, the genetic algorithm might stagnate at local optimum points. In this work a new dynamic
mutation operator with variable mutation rate is proposed. This operator does not require any pre-fixe
d
parameter. It dynamically takes into account the size (number of bits) of the individual during runtime an
d
replaces a randomly selected section of the individual by a randomly generated bit string of the same size.
All the bits of the randomly generated string are not necessarily different from bits of the selected section
from the individual. Experimentation with 17 test functions, 34 test cases and 1020 test runs proved the
superiority of the proposed dynamic mutation operator over single-point mutation operator with 1%, 5% an
d
8% mutation rates and the multipoint mutation operator with 5%, 8% and 15% mutation rates.
1 INTRODUCTION
Evolutionary algorithms are heuristic algorithms,
which imitate the natural evolutionary process and
try to build better solutions by gradually improving
present solution candidates. It is generally accepted
that any evolutionary algorithm must have five basic
components: 1) a genetic representation of a number
of solutions to the problem, 2) a way to create an
initial population of solutions, 3) an evaluation
function for rating solutions in terms of their
“fitness”, 4) “genetic” operators that alter the genetic
composition of offspring during reproduction, 5)
values for the parameters, e.g. population size,
probabilities of applying genetic operators
(Michalewicz, 1996).
A genetic algorithm is an evolutionary algorithm,
which starts the solution process by randomly
generating the initial population and then refining
the present solutions through natural like operators,
like crossover and mutation. The behaviour of the
genetic algorithm can be adjusted by parameters,
like the size of the initial population, the number of
times genetic operators are applied and how these
genetic operators are implemented. Deciding on the
best possible parameter values over the genetic run
is a challenging task, which has made researchers
busy with developing even better and efficient
techniques than the existing ones.
2 GENETIC ALGORITHM
Most often genetic algorithms (GAs) have at least
the following elements in common: populations of
chromosomes, selection according to fitness,
crossover to produce new offspring, and random
mutation of new offspring.
A simple GA works as follows: 1) A population of
n
l
-bit strings (chromosomes) is randomly
generated, 2) the fitness
)(xf of each chromosome
x
in the population is calculated, 3) chromosomes
are selected to go through crossover and mutation
operators with
c
p and
m
p probabilities respectively,
4) the old population is replaced by the new one, 5)
the process is continued until the termination
conditions are met.
However, more sophisticated genetic algorithms
typically include other intelligent operators, which
54
Moghadampour G..
RANDOM BUILDING BLOCK OPERATOR FOR GENETIC ALGORITHMS.
DOI: 10.5220/0003441400540062
In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 54-62
ISBN: 978-989-8425-54-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

apply to the specific problem. In addition, the whole
algorithm is normally implemented in a novel way
with user-defined features while for instance
measuring and controlling parameters, which affect
the behaviour of the algorithm.
2.1 Genetic Operators
For any evolutionary computation technique, the
representation of an individual in the population and
the set of operators used to alter its genetic code
constitute probably the two most important
components of the system. Therefore, an appropriate
representation (encoding) of problem variables must
be chosen along with the appropriate evolutionary
computation operators. The reverse is also true;
operators must match the representation. Data might
be represented in different formats: binary strings,
real-valued vectors, permutations, finite-state
machines, parse trees and so on. Decision on what
genetic operators to use greatly depends on the
encoding strategy of the GA. For each
representation, several operators might be employed
(Michalewicz, 2000). The most commonly used
genetic operators are crossover and mutation. These
operators are implemented in different ways for
binary and real-valued representations. In the
following, these operators are described in more
details.
2.1.1 Crossover
Crossover is the main distinguishing feature of a
GA. The simplest form of crossover is single-point:
a single crossover position is chosen randomly and
the parts of the two parents after the crossover
position are exchanged to form two new individuals
(offspring). The idea is to recombine building blocks
(schemas) on different strings. However, single-
point crossover has some shortcomings. For
instance, segments exchanged in the single-point
crossover always contain the endpoints of the
strings; it treats endpoints preferentially, and cannot
combine all possible schemas. For example, it
cannot combine instances of 11*****1 and
****11** to form an instance of 11***11*(Mitchell,
1998). Moreover, the single-point crossover suffers
from “positional bias” (Mitchell, 1998): the location
of the bits in the chromosome determines the
schemas that can be created or destroyed by
crossover.
Consequently, schemas with long defining lengths
are likely to be destroyed under single-point
crossover. The assumption in single-point crossover
is that short, low-order schemas are the functional
building blocks of strings, but the problem is that the
optimal ordering of bits is not known in advance
(Mitchell, 1998). Moreover, there may not be any
way to put all functionally related bits close together
on a string, since some particular bits might be
crucial in more than one schema. This might happen
if for instance in one schema the bit value of a locus
is 0 and in the other schema the bit value of the same
locus is 1. Furthermore, the tendency of single-point
crossover to keep short schemas intact can lead to
the preservation of so-called hitchhiker bits. These
are bits that are not part of a desired schema, but by
being close on the string, hitchhike along with the
reproduced beneficial schema (Mitchell, 1998).
In two-point crossover, two positions are chosen at
random and the segments between them are
exchanged. Two-point crossover reduces positional
bias and endpoint effect, it is less likely to disrupt
schemas with large defining lengths, and it can
combine more schemas than single-point crossover
(Mitchell, 1998). Two-point crossover has also its
own shortcomings; it cannot combine all schemas.
Multipoint-crossover has also been implemented,
e.g. in one method, the number of crossover points
for each parent is chosen from a Poisson distribution
whose mean is a function of the length of the
chromosome. Another method of implementing
multipoint-crossover is the “parameterized uniform
crossover” in which each bit is exchanged with
probability
p
, typically 8.05.0 ≤≤ p (Mitchell,
1998). In parameterized uniform crossover, any
schemas contained at different positions in the
parents can potentially be recombined in the
offspring; there is no positional bias. This implies
that uniform crossover can be highly disruptive of
any schema and may prevent coadapted alleles from
ever forming in the population (Mitchell, 1998).
There has been some successful experimentation
with a crossover method, which adapts the
distribution of its crossover points by the same
process of survival of the fittest and recombination
(Michalewicz, 1996). This was done by inserting
into the string representation special marks, which
keep track of the sites in the string where crossover
occurred. The hope was that if a particular site
produces poor offspring, the site dies off and vice
versa.
The one-point and uniform crossover methods
have been combined by some researchers through
extending a chromosomal representation by an
additional bit. There has also been some
experimentation with other crossovers: segmented
crossover and shuffle crossover (Eshelman et al.,
RANDOM BUILDING BLOCK OPERATOR FOR GENETIC ALGORITHMS
55

1991; Michalewicz, 1996). Segmented crossover, a
variant of the multipoint, allows the number of
crossover points to vary. The fixed number of
crossover points and segments (obtained after
dividing a chromosome into pieces on crossover
points) are replaced by a segment switch rate, which
specifies the probability that a segment will end at
any point in the string. The shuffle crossover is an
auxiliary mechanism, which is independent of the
number of the crossover points. It 1) randomly
shuffles the bit positions of the two strings in
tandem, 2) exchanges segments between crossover
points, and 3) unshuffles the string (Michalewicz,
1996). In gene pool recombination, genes are
randomly picked from the gene pool defined by the
selected parents.
There is no definite guidance on when to use
which variant of crossover. The success or failure of
a particular crossover operator depends on the
particular fitness function, encoding, and other
details of GA. Actually, it is a very important open
problem to fully understand interactions between
particular fitness function, encoding, crossover and
other details of a GA. Commonly, either two-point
crossover or parameterized uniform crossover has
been used with the probability of occurrence
8.07.0 −≈p (Mitchell, 1998).
Generally, it is assumed that crossover is able to
recombine highly fit schemas. However, there is
even some doubt on the usefulness of crossover, e.g.
in schema analysis of GA, crossover might be
considered as a “macro-mutation” operator that
simply allows for large jumps in the search space
(Mitchell, 1998).
2.1.2 Mutation
The common mutation operator used in canonical
genetic algorithms to manipulate binary strings
A
A
}1,0{),...(
1
=∈= Iaaa of fixed length A was
originally introduced by Holland (Holland, 1975) for
general finite individual spaces
A
AAI ...
1
×= , where
},...,{
1
l
k
iii
A
α
α
= . By this definition, the mutation
operator proceeds by:
i. determining the position
}),...,1{(,...,
1
liii
jh
∈ to
undergo mutation by a uniform random
choice, where each position has the same
small probability
m
p of undergoing mutation,
independently of what happens at other
position
ii. forming the new vector
),...,,,...,,,,...,(
11
1
1
1
1
1
1 A
a
i
a
i
a
i
aa
i
aaa
i
a
hhh
ii
+−
+−
′
′
=
′
,
where
ii
Aa
∈
′
is drawn uniformly at random
from the set of admissible values at position
i .
The original value
i
a at a position undergoing
mutation is not excluded from the random choice of
ii
Aa ∈
′
. This implies that although the position is
chosen for mutation, the corresponding value might
not change at all (Bäck et al., 2000).
Mutation rate is usually very small, like 0.001
(Mitchell, 1998). A good starting point for the bit-
flip mutation operation in binary encoding is
L
P
m
1
=
, where L is the length of the chromosome
(Mühlenbein, 1992). Since
L
1
corresponds to
flipping one bit per genome on average, it is used as
a lower bound for mutation rate. A mutation rate of
range
[
]
01.0,005.0∈
m
P is recommended for binary
encoding (Ursem, 2003). For real-value encoding
the mutation rate is usually
[]
9.0,6.0∈
m
P and the
crossover rate is
[
]
0.1,7.0∈
m
P
(Ursem, 2003).
Crossover is commonly viewed as the major
instrument of variation and innovation in GAs, with
mutation, playing a background role, insuring the
population against permanent fixation at any
particular locus (Mitchell, 1998; Bäck et al., 2000).
Mutation and crossover have the same ability for
“disruption” of existing schemas, but crossover is a
more robust constructor of new schemas (Spears,
1993; Mitchell, 1998). The power of mutation is
claimed to be underestimated in traditional GA,
since experimentation has shown that in many cases
a hill-climbing strategy works better than a GA with
crossover (Mühlenbein, 1992; Mitchell, 1998).
While recombination involves more than one
parent, mutation generally refers to the creation of a
new solution from one and only one parent. Given a
real-valued representation where each element in a
population is an
n -dimensional vector
n
x
ℜ∈ , there
are many methods for creating new offspring using
mutation. The general form of mutation can be
written as:
)(xmx
=
′
(1)
where
x
is the parent vector, m is the mutation
function and
x
′
is the resulting offspring vector. The
more common form of mutation generated offspring
vector:
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
56

Mxx +=
′
(2)
where the mutation
M is a random variable. M has
often zero mean such that
xxE =
′
)(
(3)
the expected difference between the real values of a
parent and its offspring is zero (Bäck et al., 2000).
Some forms of evolutionary algorithms apply
mutation operators to a population of strings without
using recombination, while other algorithms may
combine the use of mutation with recombination.
Any form of mutation applied to a permutation must
yield a string, which also presents a permutation.
Most mutation operators for permutations are related
to operators, which have also been used in
neighbourhood local search strategies (Whitley,
2000). Some other variations of the mutation
operator for more specific problems have been
introduced in (Bäck et al., 2000). Some new
methods and techniques for applying crossover and
mutation operators have also been presented in
(Moghadampour, 2006).
It is not a choice between crossover and mutation
but rather the balance among crossover, mutation,
selection, details of fitness function and the
encoding. Moreover, the relative usefulness of
crossover and mutation change over the course of a
run. However, all these remain to be elucidated
precisely (Mitchell, 1998).
2.1.3 Other Operators and Mating
Strategies
In addition to common crossover and mutation there
are some other operators used in GAs including
inversion, gene doubling and several operators for
preserving diversity in the population. For instance,
a “crowding” operator has been used in (De Jong,
1975; Mitchell, 1998) to prevent too many similar
individuals (“crowds”) from being in the population
at the same time. This operator replaces an existing
individual by a newly formed and most similar
offspring. In (Mengshoel et al., 2008) a probabilistic
crowding niching algorithm in which subpopulations
are maintained reliably, is presented. It is argued that
like the closely related deterministic crowding
approach, probabilistic crowding is fast, simple, and
requires no parameters beyond those of classical
genetic algorithms.
The same result can be accomplished by using an
explicit “fitness sharing” function (Mitchell, 1998),
whose idea is to decrease each individual’s fitness
by an explicit increasing function of the presence of
other similar population members. In some cases,
this operator induces appropriate “speciation”,
allowing the population members to converge on
several peaks in the fitness landscape (Mitchell,
1998). However, the same effect could be obtained
without the presence of an explicit sharing function
(Smith et al., 1993; Mitchell, 1998).
Diversity in the population can also be promoted
by putting restrictions on mating. For instance,
distinct “species” tend to be formed if only
sufficiently similar individuals are allowed to mate
(Mitchell, 1998). Another attempt to keep the entire
population as diverse as possible is disallowing
mating between too similar individuals, “incest”
(Eshelman et al., 1991; Mitchell, 1998). Another
solution is to use a “sexual selection” procedure;
allowing mating only between individuals having
the same “mating tags” (parts of the chromosome
that identify prospective mates to one another).
These tags, in principle, would also evolve to
implement appropriate restrictions on new
prospective mates (Holland, 1975).
Another solution is to restrict mating spatially.
The population evolves on a spatial lattice, and
individuals are likely to mate only with individuals
in their spatial neighborhoods. Such a scheme would
help preserve diversity by maintaining spatially
isolated species, with innovations largely occurring
at the boundaries between species (Mitchell, 1998).
The efficiency of genetic algorithms has also
been tried by imposing adaptively, where the
algorithm operators are controlled dynamically
during runtime (Eiben et al. 2008). These methods
can be categorized as deterministic, adaptive, and
self-adaptive methods (Eiben & Smitt, 2007; Eiben
et al. 2008). Adaptive methods adjust the
parameters’ values during runtime based on
feedback from the algorithm (Eiben et al. 2008),
which are mostly based on the quality of the
solutions or speed of the algorithm (Smit et al.,
2009).
3 THE RANDOM BUILDING
BLOCK OPERATOR
The random building block (RBB) operator is a new
self-adaptive operator proposed here. During the
classical crossover operation, building blocks of two
or more individuals of the population are exchanged
in the hope that a better building block from one
individual will replace a worse building block in the
other individual and improve the individual’s fitness
value. However, the random building block operator
involves only one individual. The random building
RANDOM BUILDING BLOCK OPERATOR FOR GENETIC ALGORITHMS
57

block operator resembles more the multipoint
mutation operator, but it lacks the frustrating
complexity of such an operator. The reason for this
is that the random building block operator does not
require any pre-defined parameter value and it
automatically takes into account the size (number of
bits) of the individual at hand. In practice, the
random building block operator selects a section of
random length from the individual at hand and
replaces it with a randomly produced building block
of the same length.
This operator can help breaking the possible
deadlock when the classic crossover operator fails to
improve individuals. It can also refresh the
population by injecting better building blocks into
individuals, which are not currently found from the
population. Figure 1 describes the random building
block operator.
Figure 1: The random building block operator. A random
building block is generated and copied to an individual to
produce a new offspring.
This operation is implemented in the following
order: 1) for each individual
ind two crossover
points
1
cp and
2
cp are randomly selected, 2) a
random bit string
bstr of length
12
cpcpl −=
is
generated, and 3) bits between the crossover points
on the individual
ind are replaced by the bit string
bstr . The following is the pseudo code for the
random building block operator.
procedure RandomBuildingBlock
begin
select individual from the population
select crossover point
[
)
)(,0
1
individuallengthcp ∈
select crossover point
[
)
)(,0
2
individuallengthcp ∈ so that
12
cpcp ≠ and
12
cpcp >
generate random bit string rbs of
length
12
cpcpl −=
replace bits between
1
cp and
2
cp on
the individual with rbs
Figure 2: The pseudo code for the random building block
(RBB) operator.
3.1 Survivor Selection
After each operator application, new offspring are
evaluated and compared to the population
individuals. Newly generated offspring will replace
the worst individual in the population if they are
better than the worst individual. Therefore, the
algorithm is a steady state genetic algorithm.
4 EXPERIMENTATION
The random building block operator was applied as
part of a genetic algorithm to solve the following
minimization problems:
The Ackley’s function:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∑
=
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
∑
=
−−+
n
i
i
x
n
n
i
i
x
n
e
1
).2cos(
1
exp
1
2
1
2.0exp2020
π
,
where
768.32768.32
≤
≤
−
i
x
.
The Colville’s function:
22 2 22 2 2
21 1 43 3 2
2
424
100(x ) (1 ) 90( ) (1 ) 10.1(( 1)
( 1) ) 19.8( 1)( 1), where 10 10 for i 1,...4.
i
xxxxx x
xxx x
−
+− + − +− + − +
−+ − − −≤≤ =
The Griewank’s function F1:
2
1
1
1 100
( 100) cos( ) 1
4000
n
n
i
i
i
i
x
x
i
=
=
−
−
−+
∑∏
,
where
i
-600 x 600
≤
≤
.
The Rastrigin’s function:
2
1
(10cos(2)10)
n
ii
i
xx
π
=
−+
∑
,
where
i
-5.12 x 5.12
≤
≤
.
The Schaffer’s function F6:
22 2
12
2
22
12
sin 0.5
0.5
1.0 0.001( )
xx
xx
+−
+
⎡
⎤
++
⎣
⎦
,
where
100100
≤
≤
−
i
x
.
For multidimensional problems with optional
number of dimensions (
n ), the algorithm was tested
for
50 ,10 ,5 3, ,2 ,1
=
n
.
The efficiency of the random building block operator
and three versions of single-point mutation operator
(with 1%, 5% and 8% mutation rates) and three
versions of multipoint mutation operator (with 5%,
8% and 15% mutation rates) in generating better
fitness values were tested separately 30 times for
each test case. The population size was set to 12 and
the maximum number of function evaluations for
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
58
each run was set to 10,000. During each run the best
fitness value achieved during each generation was
recorded. This made it possible to figure out when
the best fitness value of the run was actually found.
Later at the end of 30 runs for each test case the
average of best fitness values and required function
evaluations were calculated for comparison. In the
following test results for comparing the random
building block operator with different versions of
mutation operator are reported.
Table 1 summarizes test results for comparing
single-point mutation operator with the random
building block operator on Ackley’s and Colville’s
functions. In the table the average of best fitness
values and required function evaluations by single-
point mutation operator (with 1%, 5% and 8%
mutation rates) and the building block operator are
reported.
Table 1: Comparison of the average of the best fitness
values achieved for Ackley’s (A1-A50) and Colville’s
(C4) functions by single-point mutation (SPM) operator
with 1%, 5% and 8% mutation rates and the random
building block (RBB) operator. In the table Fn. stands for
function, F. for fitness and FE. for function evaluations.
Fn. Operator
SPM (1%) SPM (5%) SPM (8%) RBB
F. FE. F. FE. F. FE. F. FE.
A1 0.5 2097 0.2 1410 0.5 1927 0.0 889
A2 0.8 4399 1.5 5992 0.4 2896 0.0 4278
A3 1.5 6809 1.2 6275 1.2 6326 0.0 9400
A5 1.8 9127 1.5 8393 1.8 8863 0.0 10008
A10 2.3 10020 2.5 10146 2.0 10034 2.7 10008
A50 8.0 10146 7.6 10833 6.4 11550 16.9 10008
C4 103.9 10004 35.9 9793 26.7 9648 2.8 7225
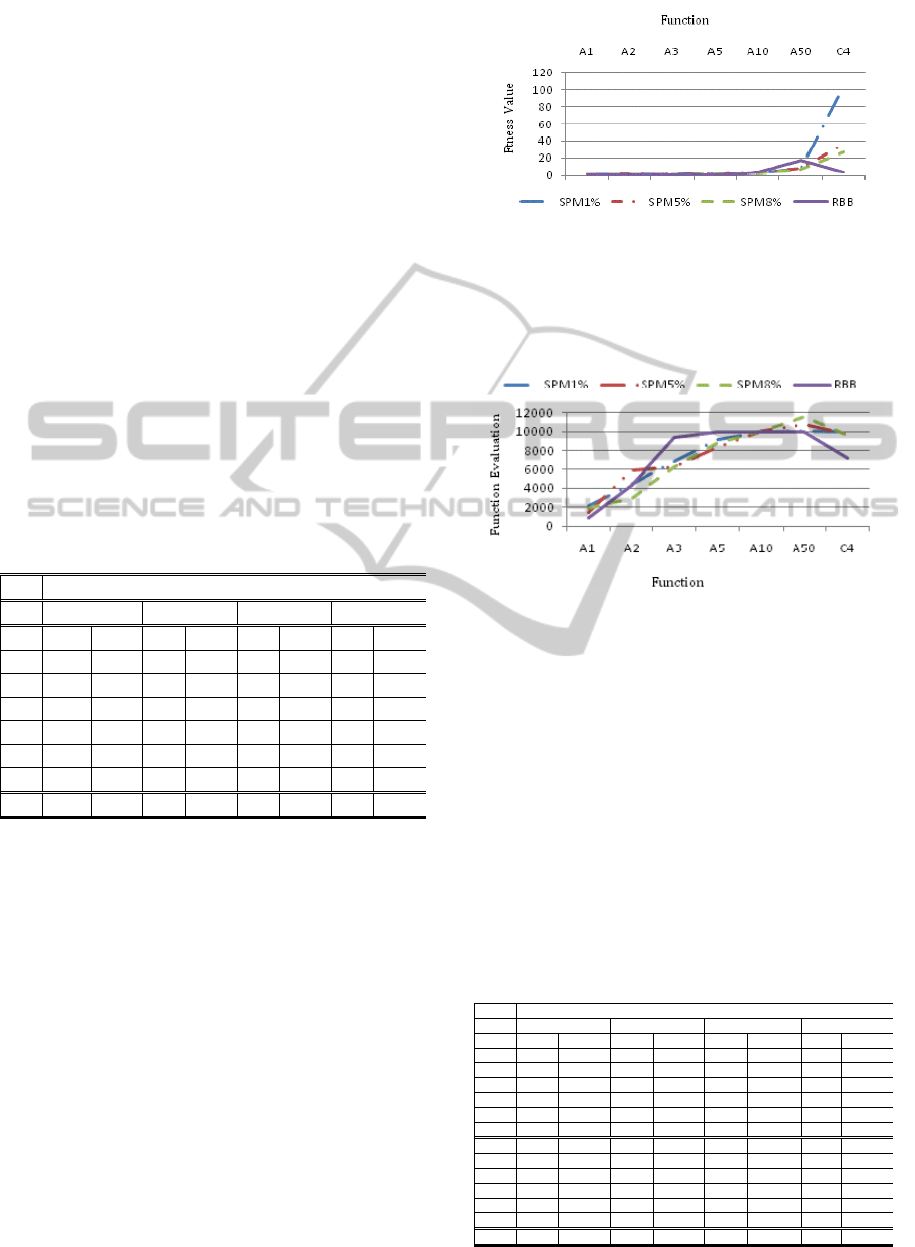
Comparing results in Table 1 indicates that the
random building block operator has produced better
results than different versions of the single-point
mutation operator in 71% of test cases. In 14% of
test cases for Ackely’s function with 10 variables the
results were almost equal. But, the random building
block operator outperformed overwhelmingly on
Colville’s function. Figure 3 demonstrates
differences between average fitness values achieved
by different operators.
In many cases it took the random building block
operator less function evaluations to achieve better
fitness values and in some other cases it achieved
better fitness values than different versions of the
single-point mutation operator although more
function evaluations were required on average.
Figure 4 illustrates differences in the average
numbers of function evaluations.
Figure 3: Comparison of average fitness values achieved
for Ackley’s (A1-A50) and Colville’s (C4) functions by
the single-point mutation operator (with 1%, 5% and 8%
mutation rates) and the random building block operator.
The optimal fitness values for all functions are zero.
Figure 4: Comparison of the average numbers of function
evaluations needed by each operator to achieve the best
fitness values for Ackley’s (A1-A50) and Colville’s (C4)
functions.
The performance of the random building block
operator against the single-point mutation operator
was also tested on the Griewank’s, Rastrigin’s and
Schaffer’s F6 functions. Table 2 summarizes the test
results.
Table 2: Comparison of the average of the best fitness
values achieved for Griewank’s (G1-G50), Rastrigin’s
(R1-R50) and Schaffer’s F6 (S2 functions by single-point
mutation (SPM) operator with 1%, 5% and 8% mutation
rates and the random building block (RBB) operator. In
the table Fn. stands for function, F. for fitness and FE. for
function evaluations.
Fn Operator
SPM (1%) SPM (5%) SPM (8%) RBB
F. FE. F. FE. F. FE. F. FE.
G1 0.0 7566 0.0 6514 0.0 7552.4 0.0 2273
G2 0.6 10005 0.7 10028 0.7 9757 0.0 8771
G3 2.1 10008 2.2 10028 2.0 10015 0.0 10008
G5 3.8 10020 4.2 10015 3.8 10130 0.1 10008
G10 10.2 10028 10.4 10069 7.1 10008 1.5 10008
G50 62 10069 63 10234 56 11455 237 10008
R1 0.8 6570 1.3 7754 0.7 6200 0.0 431
R2 3.2 9732 3.4 9765 3.7 9473 0.0 2506
R3 7.7 10003 6.3 10029 6.2 9513 0.0 6500
R5 11.4 10000 11.8 10029 10.4 10188 0.0 10008
R10 24.4 10056 25.3 10139 24.6 10166 5.4 10008
R50 156 10139 157 10111 141 11549 313 10008
S2 0.2 8874 0.1 9218 0.2 9209 0.0 9222
RANDOM BUILDING BLOCK OPERATOR FOR GENETIC ALGORITHMS
59
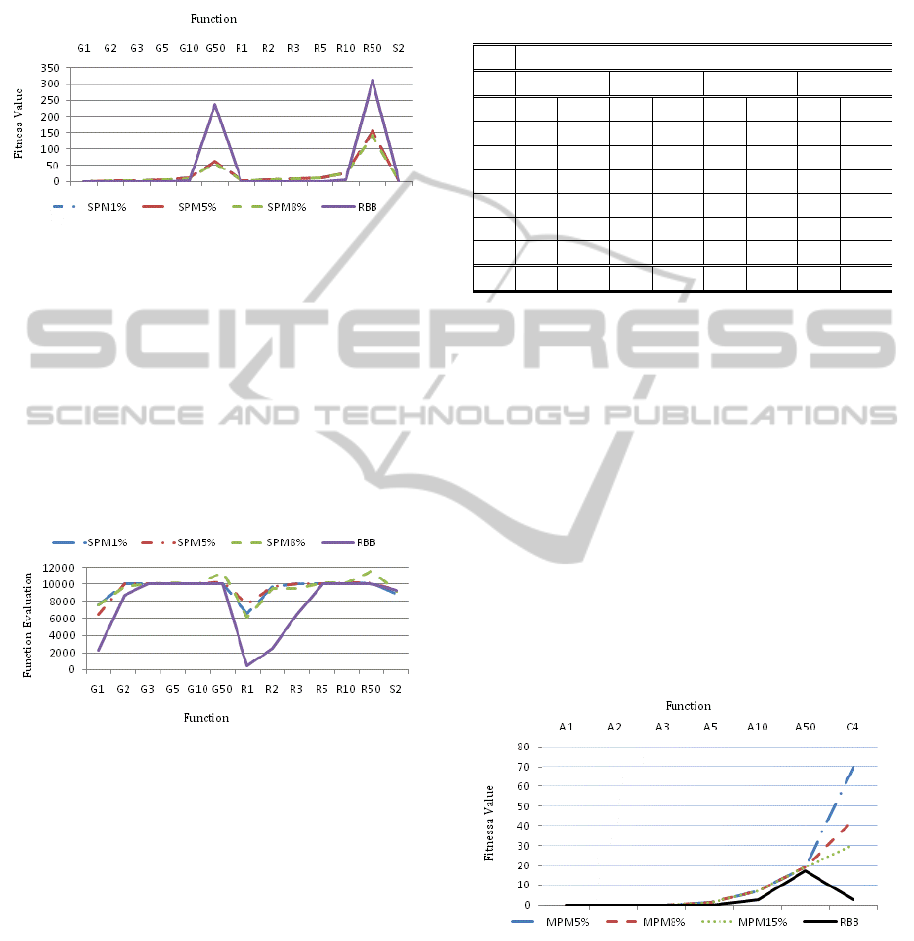
Studying data presented in Table 2 proves that the
random building block operator has been able to
produce significantly better results and in 85% of
test cases. Figure 5 illustrates the same results.
Figure 5: Comparison of the average of the best fitness
values achieved for Griewank’s (G1-G50) and Rastrigin’s
(R1-R50) functions with different variable numbers and
Schaffer’s F6 (S2) function by the single-point mutation
operator with 1%, 5% and 8% mutation rates (SPM1%,
SPM5% and SPM8%) and the random building block
(RBB) operator. The optimal fitness values for all
functions are zero.
The random building block operator achieved better
results in less function evaluations on average.
Figure 6 demonstrates differences in the average
numbers of function evaluations.
Figure 6: Comparison of the average numbers of function
evaluations needed on average by each operator to achieve
the best fitness value for Griewank’s (G1-G50),
Rastrigin’s (R1-R50) and Schaffer’s F6 (S2) functions.
The performance of the random building block
operator was also compared against the multipoint
mutation operator in which several points of the
individual were mutated during each mutation
operator. The number of points to be mutated during
each mutation operation was set to 2 times the
number of variables in the problem. This means that
if a problem had 5 variables, during each mutation
cycle, 10 points of the individual were randomly
selected to be mutated. Clearly, the total number of
mutation points was determined by the mutation
rate, which was 5%, 8% and 15% for different
experimentations.
Table 3: Comparison of best fitness values achieved for
Ackley’s (A1-A50) and Colville’s (C4) functions by
multipoint mutation (MPM) operator with 5%, 8% and
15% mutation rates and the random building block (RBB)
operator. In the table Fn. stands for function, F. for fitness
and FE. for function evaluations.
Fn. Operator
MPM (5%) MPM (8%) MPM (15%) RBB
F. FE. F. FE. F. FE. F. FE.
A1 0.0 6505 0.0 5249 0.0 4966 0.0 889
A2 0.0 10008 0.0 9817 0.0 9929 0.0 4278
A3 0.0 10008 0.0 10004 0.0 10032 0.0 9400
A5 1.1 10008 1.1 10004 1.3 10032 0.0 10008
A10 7.2 10008 6.9 10004 7.1 10032 2.7 10008
A50 19.2 10008 19.2 10004 19.2 10032 16.9 10008
C4 69.9 10000 43.1 9793 30.6 9648 2.8 7225
Comparing results reported in Table 3 proves that
the fitness values achieved by the building block
operator have been clearly better than the ones
achieved by different versions of the multipoint
mutation operator in all cases. Differences between
the average fitness values achieved for Colville
function by the random building block and different
versions of multipoint mutation operator are even
more substantial. The random building block
operator achieved an average fitness value of 2.7833
within average 7225 function evaluations, while the
multipoint mutation operator with 15% mutation rate
has achieved its best average fitness value of 26.66
within up to 9648 function evaluations. Figure 7
demonstrates differences between average fitness
values achieved by different operators.
Figure 7: Comparison of average fitness values achieved
for Ackley’s (A1-A50) and Colville’s (C4) functions by
the multipoint mutation (with 5%, 8% and 15% mutation
rates) and the random building block operator. The
optimal fitness values for all functions are zero.
Moreover, the best fitness values have been
achieved within less function evaluations with the
random building operator. Figure 8 depicts the
summary of differences in the number of function
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
60
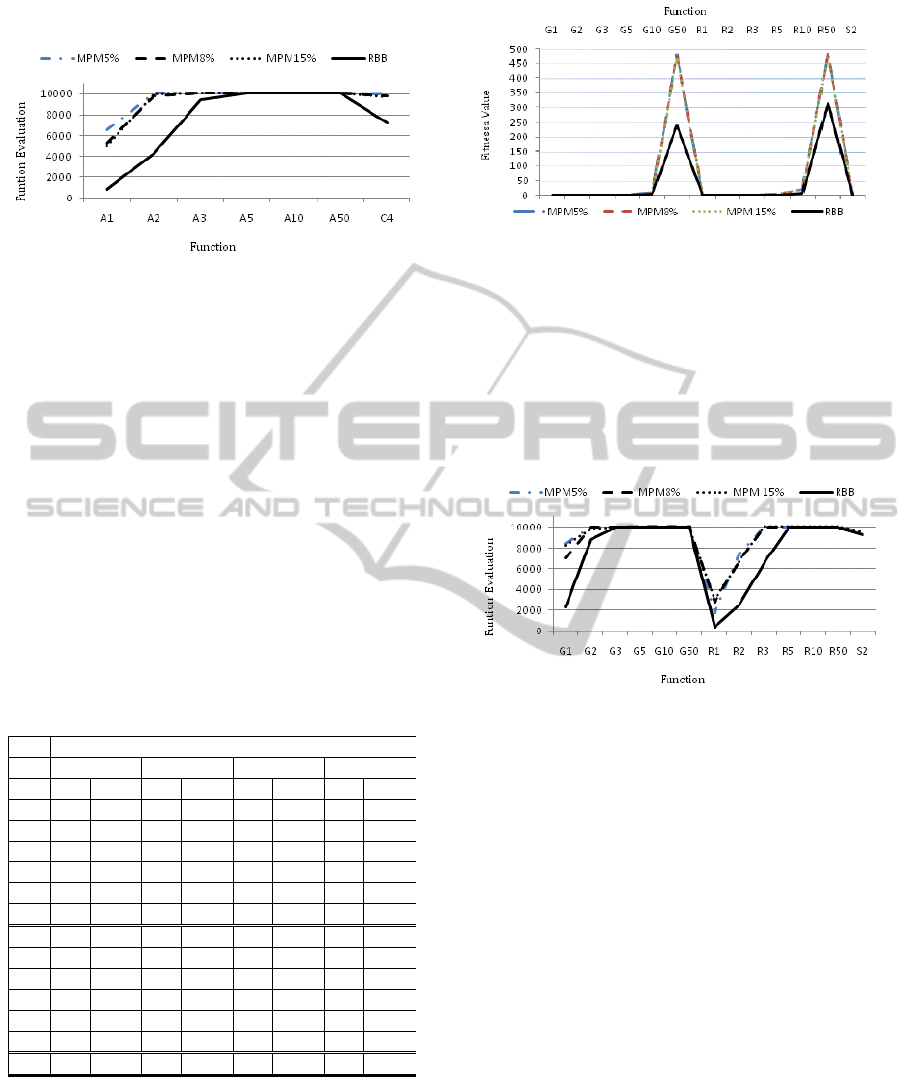
evaluations.
Figure 8: Comparison of the average numbers of function
evaluations needed by each operator to achieve the best
fitness values for Ackley’s (A1-A50) and Colville’s (C4)
functions.
As it can clearly be seen from Figure 8, the random
building block operator has in many cases needed
much less function evaluations to achieve the best
fitness values. The performance of the random
building block operator against the multipoint
mutation operator was also tested on Griewank’s,
Rastrigin’s and Schaffer’s F6 functions. Table 4
summarizes the test results.
Table 4: Comparison of the average of best fitness values
achieved for Griewank’s (G1-G50), Rastrigin’s (R1-R50)
and Schaffer’s F6 (S2) functions by multipoint mutation
(MPM) operator with 5%, 8% and 15% mutation rates and
the random building block (RBB) operator. In the table
Fn. stands for function, F. for fitness and FE. for function
evaluations.
Fn. Operator
MPM (5%) MPM (8%) MPM (15%) RBB
F. FE. F. FE. F. FE. F. FE.
G1 0.0 8490 0.0 7002 0.0 8253 0.0 2273
G2 0.0 10004 0.0 10008 0.0 9759 0.0 8771
G3 0.2 10004 0.1 10008 0.1 10008 0.0 10008
G5 1.0 10008 1.1 10014 0.9 10008 0.1 10008
G10 8.1 10008 6.1 10014 7.1 10008 1.5 10008
G50 479 10008 475 10014 468 10008 237 10008
R1 0.1 1768 0.2 2861 0.3 2973 0.0 431
R2 0.2 7341 0.2 6652 0.2 6630 0.0 2506
R3 0.3 10008 0.3 10008 0.3 10012 0.0 6500
R5 2.1 10008 2.3 10008 2.5 10012 0.0 10008
R10 22 10008 22 10008 22 10012 5 10008
R50 485 10008 485 1008 475 10012 313 10008
S2 0.0 9518 0.0 9383 0.0 9478 0.0 9222
Studying results presented in Table 4 proves that
compared to different versions of the multipoint
mutation operator, the random building block
operator has achieved better fitness values within
less function evaluations on average. These results
can also be observed from Figure 9.
Figure 9: Comparison of average fitness values achieved
for Griewank’s (G1-G50), Rastrigin’s (R1-50) and
Schaffer’s F6 (S2) functions by the multipoint mutation
operator with 5%, 8% and 15% mutation rates (MPM5%,
MPM8% and MPM15%) and the random building block
(RBB) operator. The optimal fitness values for all
functions are zero.
Figure 10 depicts the summary of differences in the
number of function evaluations.
Figure 10: Comparison of the average numbers of function
evaluations needed by each operator to achieve the best
fitness value for Griewank’s (G1-G50), Rastrigin’s (R1-
R50) and Schaffer’s F6 (S2) functions.
Figure 10 clearly indicates that compared to
different versions of multipoint mutation operator,
the random building block operator has needed less
function evaluations to achieve the best fitness
values on average.
5 CONCLUSIONS
In this paper a dynamic mutation operator; random
building block operator for genetic algorithms was
proposed. The operator was described and utilized in
solving five well-known test problems. The operator
was tested in 1020 runs for 34 test cases. For each
test case, the performance of the random building
block operator was tested against single-point
mutation operator with 1%, 5% and 8% mutation
rates and multipoint mutation operator with 5%, 8%
and 15% mutation rates. The maximum limit of the
RANDOM BUILDING BLOCK OPERATOR FOR GENETIC ALGORITHMS
61

function evaluations was set to around 10,000. Each
test case was repeated 30 times and the average of
the best fitness values and the average numbers of
function evaluations required for achieving the best
fitness value were calculated. Comparing test results
revealed that the random building block operator
was capable of achieving better fitness values within
less function evaluations compared to different
versions of single-point and multipoint mutation
operators. The fascinating feature of random
building block is that it is dynamic and therefore
does not require any parameterization. However, for
mutation operators the mutation rate and the number
of mutation points should be set in advance. The
random building block can be used straight off the
shelf without needing to know its best recommended
rate. Hence, it lacks frustrating complexity, which is
typical for different versions of the mutation
operator. Therefore, it can be claimed that the
random building block is superior to the mutation
operator and capable of improving individuals in the
population more efficiently.
5.1 Future Research
The proposed operator can be combined with other
operators and applied to new problems and its
efficiency in helping the search process can be
evaluated more thoroughly with new functions.
Moreover, the random building block operator can
be adopted as part of the genetic algorithm to
compete with other state-of-the-art algorithms on
solving more problems.
REFERENCES
Eiben, A. and J. Smith, 2007. Introduction to Evolutionary
Computing. Natural Computing Series. Springer, 2nd
edition.
Bäck, Thomas, David B. Fogel, Darrell Whitely & Peter
J. Angeline, 2000. Mutation operators. In:
Evolutionary Computation 1, Basic Algorithms and
Operators. Eds T. Bäck, D.B. Fogel & Z.
Michalewicz. United Kingdom: Institute of Physics
Publishing Ltd, Bristol and Philadelphia. ISBN
0750306645.
De Jong, K. A., 1975. An Analysis of the Behavior of a
Class of Genetic Adaptive Systems. Ph.D. thesis,
University of Michigan. Michigan: Ann Arbor.
Eshelman, L. J. & J.D. Schaffer, 1991. Preventing
premature convergence in genetic algorithms by
preventing incest. In Proceedings of the Fourth
International Conference on Genetic Algorithms. Eds
R. K. Belew & L. B. Booker. San Mateo, CA :
Morgan Kaufmann Publishers.
Eiben, G. and M. C. Schut, 2008. New Ways To Calibrate
Evolutionary Algorithms. In Advances in
Metaheuristics for Hard Optimization, pages 153–177.
Holland, J. H., 1975. Adaptation in Natural and Artificial
Systems. Ann Arbor: MI: University of Michigan
Press.
Mengshoel, Ole J. & Goldberg, David E., 2008. The
crowding approach to niching in genetic algorithms.
Evolutionary Computation, Volume 16 , Issue 3 (Fall
2008). ISSN:1063-6560.
Michalewicz, Zbigniew (1996). Genetic Algorithms +
Data Structures = Evolution Programs. Third,
Revised and Extended Edition. USA: Springer. ISBN
3-540-60676-9.
Michalewicz, Zbigniew, 2000. Introduction to search
operators. In Evolutionary Computation 1, Basic
Algorithms and Operators. Eds T. Bäck, D.B. Fogel &
Z. Michalewicz. United Kingdom: Institute of Physics
Publishing Ltd, Bristol and Philadelphia. ISBN
0750306645.
Mitchell, Melanie, 1998. An Introducton to Genetic
Algorithms. United States of America: A Bradford
Book. First MIT Press Paperback Edition.
Moghadampour, Ghodrat, 2006. Genetic Algorithms,
Parameter Control and Function Optimization: A New
Approach. PhD dissertation. ACTA WASAENSIA
160, Vaasa, Finland. ISBN 952-476-140-8.
Mühlenbein, H., 1992. How genetic algorithms really
work: 1. mutation and hill-climbing. In: Parallel
Problem Solving from Nature 2. Eds R. Männer & B.
Manderick. North-Holland.
Smit, S. K. and Eiben, A. E., 2009. Comparing Parameter
Tuning Methods for Evolutionary Algorithms. In IEEE
Congress on Evolutionary Computation (CEC), pages
399–406, May 2009.
Smith, R. E., S. Forrest & A.S. Perelson, 1993.
Population diversity in an immune system model:
implications for genetic search. In
Foundations of
Genetic Algorithms 2. Ed. L.D. Whitely. Morgan
Kaufmann.
Spears, W. M., 1993. Crossover or mutation? In:
Foundations of Genetic Algorithms 2. Ed. L. D.
Whitely. Morgan Kaufmann.
Ursem, Rasmus K., 2003. Models for Evolutionary
Algorithms and Their Applications in System
Identification and Control Optimization (PhD
Dissertation). A Dissertation Presented to the Faculty
of Science of the University of Aarhus in Partial
Fulfillment of the Requirements for the PhD Degree.
Department of Computer Science, University of
Aarhus, Denmark.
Whitley, Darrell, 2000. Permutations. In Evolutionary
Computation 1, Basic Algorithms and Operators. Eds
T. Bäck, D. B. Fogel & Z. Michalewicz. United
Kingdom: Institute of Physics Publishing Ltd, Bristol
and Philadelphia. ISBN 0750306645.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
62
