A NEW METHOD AND METRIC FOR QUANTITATIVE RISK

ANALYSIS

Peng Zhou and Hareton K. N. Leung

Department of Computing, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong

Keywords: Risk prioritization, Risk metrics, Risk exposure, Risk intensity, Risk impact assessment, Risk management.

Abstract: Quantitative risk analysis provides practitioners a deeper understanding of the risks in their projects.

However, the existing methods for impact assessment are inaccurate and the metrics for risk prioritization

also can not properly prioritize the risks for certain cases. In this paper, we propose a method for measuring

risk impact by using AHP. We also propose a new indicator, risk intensity (RI), to prioritize the risks of a

project. Compared with the widely used metric Risk Exposure (RE), the contours of RI show a convex

pattern whereas the contours of RE show a concave pattern. RI allows practitioners weight probability and

risk impact differently and can better satisfy the needs of risk prioritization. Through a case study, we found

that RI could better prioritize the risks than RE.

1 INTRODUCTION

Nowadays, Information Technology (IT) projects

become more and more complicate, and face many

challenges and uncertain factors. To guarantee the

success of IT projects, effective risk management is

necessary. Most of the failed projects are caused by

poor risk management (Sherer, 2004).

As one of the key processes of risk management

model proposed by Project Management Institute

(PMI, 2008), quantitative risk analysis is important

since one can not manage what one does not measure.

One key output of the quantitative risk analysis is a

prioritized list of quantified risks. For accurate risk

prioritization, two preconditions are needed: 1)

accurate assessment of the probability of the

occurrence of risk and the impact of the risk, 2) a

good metric to determine the priority of risks.

There are some easy to use guidelines and

principles for assessing probability. (Mcmanus, 2004;

Pandian, 2007; Ferguson, 2004; Boehm, 1991)

Compared with the assessment of risk probability,

the assessment of risk impact is more complicate

since the impact may affect different aspects of a

project, such as schedule, cost, scope, and quality of

the product and service. Our investigation on the

existing methods for assessing risk impact found that

the existing methods are inaccurate.

Risk Exposure (RE) is a commonly used metric

for quantitative risk analysis and risk prioritization.

However, it can not properly prioritize the risks for

certain cases. Boehm (1989) also pointed out this

problem when he proposed RE.

In summary, in order to properly prioritize the

risks, we need a method for accurately assessing risk

impact and a new way to address the priority of the

risk. In this paper, we will propose a method for

measuring risk impact by using AHP. Then, we

proposed a new indicator, risk intensity (RI), to

prioritize the risks of a project. RI could overcome

the shortcoming of RE in risk prioritizing and

properly address the priority of the risk. The aim of

this paper is to develop a better method and a new

metric that help practitioners to assess the risks

accurately and prioritize the risks properly, thus

supporting more effective risk management.

The rest of the paper is organized as follow. We

present the related work in section 2. Then, we

propose a method for accurately assessing risk

impact and a new metric for properly prioritizing the

risks in section 3 and section 4 respectively. At last,

we draw a conclusion and address the future study in

section 5.

2 RELATED WORK

2.1 Definition of Risk

Glutch (1994) defined risk as:

Zhou P. and Leung H..

A NEW METHOD AND METRIC FOR QUANTITATIVE RISK ANALYSIS.

DOI: 10.5220/0003442200250033

In Proceedings of the 13th International Conference on Enterprise Information Systems (ICEIS-2011), pages 25-33

ISBN: 978-989-8425-55-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Risk is the combination of the probability of an

abnormal event or failure and the consequence(s)

of that event or failure to a system’s operators,

users, or its environment.

Although there are other definitions (Boehm,

1989; Mcmanus, 2004; Pandian, 2007), a risk has

two basic attributes, probability (P), and impact (I),

where probability is the probability of risk

occurrence, and impact is the level of damage if risk

occurs. Recent risk management literatures have

broadened the definition of risk to include

opportunity (PMI, 2008; Kähkönen, 2001).

According to PMI (2008), a project risk is an event

that can have either positive or negative effect on

project objectives. An event offers risk if I > 0, and it

offers opportunity if I < 0.

According to probability theory, P theoretically

ranges in [0, 1]. The range of I does not have any

theoretical boundaries. However, we can assess it on

a relative scale which range from -i to +i, or

normalize the scale to [-1, 1]. In this paper, we assess

the impact with the latter scale.

Not all events can be considered as risks. White

(2006) argues that three kinds of events are not risk.

An event is not a risk if it:

 never happens (P = 0);

 happens without any impact (I = 0);

 surely happens (P = 1).

In summary, we can use R:(P, I) to denote a risk,

where P is a real number in (0, 1), and I is a real

number in [-1, 1] and does not equal to 0 (I

∈

[-1,

∪ (0, 1] ).

For convenient, the risk impact is considered as

negative if we do not specify otherwise. All the

results which are based on the negative impact can

easily extend to the positive impact, since the

formulas can be directly extended from (0, 1] to [-1,

0) and the discussion based on the range of (0, 1] is

also suitable for [-1, 0).

In risk management, those risks with very high

impacts are called hazards. According to Pandian

(2007), in hazard analysis we do not discount a

hazard. Instead we apply Murphy's law: If something

can go wrong, it will go wrong. Similarly, those risks

with high probability are considered as constraints of

the project since there is no surprise element

(Pandian, 2007). In summary, the risks with high

probability or high impact should have a higher

priority than those risks with relatively low

probability and impact (Boehm, 1989; Mcmanus,

2004; Pandian, 2007).

Risk matrix is a widely used qualitative method

for ranking risks (PMI, 2008; Cox, et al, 2005; Cox,

2008). A risk matrix is a table that has several

categories of probability for its rows (or columns)

and several categories of risk impact for its columns

(or rows) respectively. The gray level indicates the

priority of the risks. The deeper gray means higher

risk. The risk level of each region in the risk matrix

should reflect the opinions of stakeholders. Although

people may argue that risk matrix may not rank the

risks accurately (Cox, et al, 2005; Cox, 2008), it can

serve as the basis of quantitative risk analysis. It

provides us the distribution pattern of risks’ priority

at least. Although different projects may use different

risk matrix, the risks with high probability and/or

impact should have high priority. We can use a

typical 5x5 risk matrix to represent this pattern (see

Fig. 1). From Fig. 1, we find that the risk with high

probability or high impact should have a higher

priority than those risks with relatively low

probability and impact. For example, a risk in

(Frequently, Insignificant) region and a risk in

(Seldom, Catastrophic) region should have higher

priority than any risks in the region formed by

(Possible, Unlikely, Seldom) and (Moderate, Minor,

Insignificant).

Frequently

Likely

Possible

Unlikely

Seldom

Probability

Impact

Insignific

ant

Minor Moderate Major Catastrop

hic

Figure 1: A risk matrix.

2.2 Assessment of Risk Impact

One way to assess the risk impact is approximate it

without working out the impacts in different

dimensions, such as time, budget, quality, and scope

(Mcmanus, 2004; Boehm,1991). For example, we

can assess the impacts on a relative scale of (0, 10].

This is commonly used in practice because of its

simplicity. However, this kind of method is

inaccurate.

Very few studies assess the risk impact with due

consideration of the impact of risk in different

dimensions of IT projects. The method proposed by

Ferguson (2004) for assessing risk impact does not

integrate the impact in different dimensions properly.

The basic idea of his method is first divide the risk

impact into 5 levels. Each level associates with a

benchmark and an impact score. The benchmark of

the 5

level is established according to the project.

Then, the benchmarks of lower levels are 1/3 of its

immediate upper level. The impact score is

calculated as

Impact score = 3

eve

-1

)

(1)

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

Each risk can be classified into one impact level

based on practitioners’ judgment and assigned the

impact score of that level. For example, assume a

project, “Project A”, will take 18 months with a

project cost of $3 million, and expect to achieve $1

million revenue in the first year. The benchmark and

the impact score of each level is shown in Table 1.

Then, a risk is assigned an impact score of 9 if it is

classified into level 3.

Table 1: Benchmark and impact score of “Project A”.

Impact

Level

Benchmark

Impact

Score

z Overrun by 18 months.

z Overspend by $3M.

z Lose $1M in revenue.

z Overrun by 6 months.

z Overspend by $1M.

z Lose $333K in revenue.

z Overrun by 2 months.

z Overspend by 333K.

z Lose $111K in revenue.

z Overrun by 3 weeks.

z Overspend by $111K.

z Lose $37K in revenue.

z Overrun by 1 week.

z Overspend by $37K.

z Lose $12K in revenue.

This method has two major problems. First, the

granularity is too big to accurately assess the risk

impact. For example, assume that two risks have

impacts in overrun by 4 months and 8 months

respectively. Although they have significant

difference in overrun, they are assigned the same

impact value of 27. Second, it does not consider the

impacts in different impact dimensions. For example,

assume that one risk has impact in overrun by 6

months and overspend by 500K, and the other has

impact in overrun by 6 months and overspend by

100K. Although their overspendings are significantly

different, they may be classified into the same impact

level of 3 according to their major impact in time

dimension and then are assigned the same impact

value of 27.

2.3 Risk Exposure (RE)

RE was introduced by Boehm (1989), and defined as

the multiplication of probability and impact of the

risk.

EPI=×

(2)

Although RE is widely used and accepted by

most practitioners, we find that RE can not properly

prioritize the risks. Fig. 2 shows RE contours as a

function of probability and impact, where both

probability and impact range from 0 to 1.

Probability

Impact

RE=0.10

RE=0.25

0 1

RE=0.50

Figure 2: Contours of RE.

From Fig. 2, we can find that risks with high

probability and low impact, or high impact and low

probability, have the same RE value as those risks

with relatively low probability and risk. For example,

let’s consider four risks as shown in Table 2. Three

of them, risk

a, b, and c, have the same RE value

0.18. Then, they will have the same priority in risk

response process if we use RE to prioritize risks.

Further, as risk

d has the highest RE value among all

four risks, it has the highest priority. However, risk

and

b should have a higher priority than risk c and d,

because the risks with high probability or high

impact should have a higher priority than those risks

with relatively low probability and impact (Boehm,

1989; Mcmanus, 2004; Pandian, 2007). As

demonstrated in this example, we find that RE can

not properly prioritize the risks for certain cases.

Table 2: Four risks and their RE.

Risk Probability Impact RE

a 0.9 0.2 0.18

b 0.2 0.9 0.18

c 0.4 0.45 0.18

d 0.45 0.45 0.20

2.4 Analytic Hierarchy Process (AHP)

Analytic Hierarchy Process (AHP) has been

extensively studied and refined since it was proposed

twenty years ago (Saaty, 1994; Lipovetsky, 1996;

Lipovetsky and Tishler, 1994; Forman and Gass,

2001). It is a structured technique for decision

making. The AHP is most useful when people work

on complex problems which include different stakes

and involve human perceptions and judgment

(Bhushan and Rai, 2004). It calculates a numerical

value, global rating, for alternatives which can be

processed and compared over the entire range of the

problem. The global rating can also be used to

evaluate objects with multiple dimensions (Bhushan

and Rai, 2004; Forman and Gass, 2001). Note that,

although there are many versions of AHP (Bhushan

A NEW METHOD AND METRIC FOR QUANTITATIVE RISK ANALYSIS

and Rai, 2004), we will use the standard approach in

this paper for its universality.

The users of AHP need to decompose the

problem into a hierarchy of goal, criteria, sub-criteria

and alternatives first. Then, the weighted-sum

method (WSM) is used for evaluating each

alternative. We can get the weighted rating in each

criterion by multiplying the rating of alternatives in

each criterion and the importance of the criterion.

This product is summed over all the criteria to

generate the global ratings of the alternative.

Mathematically,

iijj

Rating rw

∑

(3)

where

Rating

is the rating of the i

alternative, r

the rating of the

alternative in the j

criterion, and

is the weight or importance of the j

criterion.

An important issue in using AHP is how to

weight different criteria. One way to do this is

compare all pairs of combinations. The result of the

comparisons can be represented with a square

decision matrix,

A, which is shown in (4). Each

element in the matrix,

, represents the relative

importance of the

criterion compared with the j

criterion. The measurement scale used by the AHP is

one of 1 – 9 in absolute numbers. The higher value

means higher comparative importance while 1 means

equal importance. For example, if the

criterion is

moderately more important than

criterion, then a

can be assigned 3. On the contrary,

can be

assigned 1/3. Based on decision matrix,

A, we can

calculate the weights of different criteria (Saaty,

1994; Bhushan and Rai, 2004).

12 1

12 2

1/ 1

1/ 1/ 1

⎛⎞

⎜⎟

⎝⎠

#%#

(4)

3 A METHOD TO ASSESS RISK

IMPACT

A risk may have potential impacts on different

dimensions of a project. For example, turnover is a

common risk of many projects. If this risk happens, it

may require some additional schedule time and

additional resource cost to hire and train staff.

Besides that, the quality of product/service may

downgrade since the new team member is not

familiar with the project.

Step 1:

Identify the complete loss for the project in four

risk dimensions: time, budget, quality and scope.

Step 2:

Measure R’s impact in each dimension based on

complete loss of that dimension.

Step 3:

Weight four dimensions and combine the risk

impacts in four dimensions using AHP.

Figure 3: Procedure for assessing risk impact.

A problem of existing methods for risk impact

assessment is they do not combine the impacts in

different dimensions. In order to assess the risk

impact accurately, practitioners can follow our

proposed procedures as shown in Fig. 3.

The first step is identifying what are the complete

loss for a project in its most important four

dimensions, time, budget, quality, and scope (PMI,

2008; Kerzner, 2006). The practitioners should

decide the complete loss in each dimension based on

the constraints and assumptions of the project. As

Jones (1996) reported that “the typical project is 100

percent over budget when it is cancelled”, in many

cases, it is a good choice to set the complete loss of

each dimension to the value that would cause the

project to be cancelled. For example, the complete

loss in the time dimension could be set to 12 months

if the schedule of the project is 12 months.

Practitioners should identify the complete loss

according to specific characteristics of their project.

We use

, k=1,…,4, to denote the complete loss in

time, budget, quality, and scope respectively.

The second step is measuring the risk impact in

each dimension based on the complete loss of that

dimension. We use

, k=1,…,4, to denote the impact

in time, budget, quality, and scope respectively. Then,

the impact of a risk can be represented as a 4-tuple,

(

, I

). For any risk, we use PL

to denote its

potential loss in the

dimension. Then, the ratio of

over CL

, can be used to rank the impact in the

dimension. Note that practitioners should confine

the

in the range of [0, CL

]. If the estimated PL

is bigger than

, practitioners can set PL

equal to

(5)

where,

ranges in [0, 1]. For example, assume a risk

has a potential loss of 6 months in the time

dimension, and the complete loss in this dimension is

18 months. That is

=18 months and PL

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

months

. Then, the risk impact in the time dimension,

= PL

/ CL

=(6 months)/(18 months) = 0.33.

The third step is weighting different impact

dimensions and then calculating the risk impact using

AHP. The practitioners can weight different impact

dimensions based on the characteristics of the project,

enterprise environment factors, past experiences, and

so on. When we use AHP to assess risk impact, the

risks of the project serve as the alternatives in AHP,

the four impact dimensions serve as the criteria in

AHP, and

serves as the rating in the k

criterion.

Then, the risk impact,

I, of a risk is the global rating

of the risk in AHP. If we use

, k=1,…,4, to denote

the weights of four impact dimensions, time, budget,

quality, and scope respectively, the risk impact,

I, is

calculated with (6) in terms of global rating of AHP.

∑

(6)

where, 0≤

≤1, 0< W

<1 and ∑ W

=1.

We next use an example and Table 3 to illustrate

the procedures of assessing risk impact. Assume

there is a project with 12 months schedule and budget

of $200K. The project has 30 quality metrics defined

in requirement and has a size of 100 function points

(FP). We also assume that practitioners found 4 risks

in risk identification. To assess the risk impact of the

risks, the practitioners should define the complete

loss in each dimension based on specific

characteristics of the project first. We assume that the

complete loss in each dimension is overrun by 2

months, overspend by $50K, failed in 5 quality

metrics and missing 30 FP respectively. That is,

=2months, CL

=$50K, CL

=5metrics, CL

=30FP.

Second, practitioners should assess the potential loss

of all risks of the project in each dimension. Assume

that the potential losses of those 4 risks in our

example were already assessed by practitioners. Then,

we can compute their impact in each dimension. The

results of this step are shown in the 5

row to 8

row

of Table 3. Third, practitioners should work out the

decision matrix based on the characteristics of the

project. The decision matrix is shown in Table 4.

This matrix shows that time and quality dimension

have equal importance, both quality and time are

moderately more important than budget and strongly

more important than scope, and budget is moderately

important over scope. Based on the decision matrix,

we can use the method defined in AHP to compute

the weight of each dimension. Practitioners can use

some tools to calculate the weight of each dimension

(For example, an online tool is available at

http://www.isc.senshu-u.ac.jp/~thc0456/EAHP/AHPweb.html.).

The weight of each dimension in this example is

= 0.379,

= 0.140, W

= 0.400, W

= 0.081. After

that, practitioners can calculate the risk impact of

each risk with (6). The results of this step are shown

in the last column of Table 3.

Note that practitioners can use other ways to

measure the complete loss and potential loss in

quality dimension and scope dimension. Our

example assumes that all quality metrics and

functions have the same importance, whereas, in real

project some quality metrics and functions are key

metrics and key functions we can not miss. If a risk

has potential impact on those key metrics and

functions, we should consider the potential loss as a

complete loss.

Note that our method can also be extended to

more dimensions. That is, practitioners can identify

other impact dimensions rather than our proposed

dimensions. To extend our method, practitioners

should identify all impact dimensions first, and then

follow the steps shown in Fig. 3 to assess the risk

impact. The only difference is that practitioners

should consider all identified risk dimensions, not

just our proposed dimensions.

Table 3: Example for assessing risk impact.

Risks

Time Budget Quality Scope

Impact

=2mont

=$50K CL

=5metric

=30FP

IIW

∑

=0.379 W

=0.140 W

= 0.400 W

=0.081

wee

metri

4 0.50 0 0.20 0 0 20 0.67 0.272

0 0 0 0.40 3 0.60 10 0.33 0.323

2 0.25 0 0.20 2 0.40 5 0.17 0.297

0 0 0 0 2 0.40 0 0.33 0.187

Table 4: Decision matrix for the example.

Time Budget Quality Scope

Time 1 3 1 4

Budget 1/3 1 1/3 2

Quality 1 3 1 5

Scope 1/4 1/2 1/5 1

We use AHP to weight different impact

dimensions and combine the impacts of different

dimensions into one single value because of

following reasons. AHP has solid mathematical basis

and “it has been applied literally to hundreds of

examples both real and hypothetical” (Saaty, 2008).

The power and validity of AHP have already been

validated in practices. Compared with the simple

weighted-sum method AHP provides a hierarchy

structure for risk assessment, which is useful when

A NEW METHOD AND METRIC FOR QUANTITATIVE RISK ANALYSIS

we want to divide impact dimensions into sub-

dimensions. It also provides us a useful method for

weighting different impact dimensions based on the

decision matrix.

The proposed method for assessing risk impact is

more accurate than other methods, such as

approximate methods and the Ferguson method,

since we not only measure the impacts of different

dimensions but also integrate them together.

4 A NEW METRIC FOR RISK

PRIORITIZATION

4.1 Risk Intensity

As mentioned earlier, RE can not properly address

the priority of the risks. We propose a new metric,

Risk Intensity (RI), to measure the priority of the risk.

We assume that a project includes a set of

n risks

at time

t, RSet(t) = {R

, R

, …, R

}. Both the

probability and the impact of

, R

∈RSet(t), and the

number of risks may change as time elapse. The new

metric, RI, should satisfy following constrains:

∀ R

:(P

, I

), R

:(P

, I

)∈RSet(t), if P

= P

and

= I

then Pri

= Pri

;

∀ R

:(P

, I

), R

:(P

, I

)∈RSet(t), if P

> P

and

> I

then Pri

> Pri

;

∀ R

:(P

, I

), R

:(P

, I

)∈RSet(t), if P

> P

and

= I

then Pri

> Pri

;

∀ R

:(P

, I

), R

:(P

, I

)∈RSet(t), if P

= P

and

> I

then Pri

> Pri

;

∀ R

:(P

, I

), R

:(P

, I

)∈ RSet(t), if (P

> P

and

< I

) or (P

< P

and I

> I

), the Pri

and

Pri

should approximately match the

pattern of the risk matrix in Fig. 1.

where,

Pri

and Pri

are the priority of risks R

and R

respectively.

A risk can be mapped to a point in the PI

(probability and impact) area (0, 1)×(0 ,1] if we only

focus on risk rather than opportunity. Fig. 4 shows

the mapping of 3 risks and their points in the 2-

dimension PI space. Risks

:(0.5, 0.5), R

:(0.1, 1),

and

:(0.9, 0.2), are mapped to points A, B, and C

respectively.

impact

robability

0 1

:(0.5,0.5)

:(0.1,1)

=1.00

=0.10

=0.92

=0.18

:(0.9,0.2)

=0.71

=0.25

Figure 4: RI and RE of risks.

Frequently

Likely

Possible

Unlikely

Seldom

Probability

Impact

Insignific

ant

Minor Moderate Major Catastrop

hic

convex concave

Figure 5: Contours and the risk matrix.

Most practitioners would accept that the risk with

higher probability and higher impact should have

higher priority. Thus, a risk that is further away from

the original point in PI space should have a higher

priority. Based on this idea and the geometric

meaning of Euclidean distance, we define RI as the

Euclidean distance between the risk point and the

original point.

IPI

+ (7)

where,

P and I are the probability and risk impact of

the risk. RI ranges in (0, 1.41). As shown in Fig. 4,

RI of risks

:(0.5, 0.5), R

:(0.1, 1), and R

:(0.9, 0.2)

are

=0.71, RI

=1, and RI

=0.92 respectively. It is

easy to verify that RI satisfies constraints 1-4. As

shown in Fig. 6, the contours of RI are convex. Thus,

RI also satisfies constraint 5.

Using the risks shown earlier in Table 2 as

example, the RI and RE of these risks are shown in

Table 5. In this example, we find that RI gives high

priority to those risks which have high probability or

high impact whereas RE does not.

Table 5: Decision matrix for the example.

Risk P I RE RI

a 0.9 0.2 0.18 0.92

b 0.2 0.9 0.18 0.92

c 0.4 0.45 0.18 0.60

d 0.45 0.45 0.20 0.64

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

The most important advantage of RI over RE is

that RI matches the risk matrix well while RE not.

Fig. 6 shows contours of RI and RE respectively. It is

easy to find that the RI contours are convex while the

RE contours are concave. RI is more accurate than

RE in risk prioritization when the risk matrix used in

the project shows a convex pattern.

impact

robability

0 1

RE=0.5

RI =1.12

RE=0.25

RI =1.03

RE=0.10

RI =1.01

Figure 6: Contours of RI and RE.

In risk management, we apply different strategies

for dealing with the risks according to the specific

circumstances of the project. Sometimes, the

practitioners may consider the risk impact slightly

more important than probability. For other cases, the

practitioners may consider the probability slightly

more important than impact. However, both RI in (7)

and RE give equal weight to probability and risk

impact. For example, there are two risks, R

:(0.9,

0.2), and R

:(0.2, 0.9). If we want to give a higher

weight for risk impact in prioritizing risks (that is, R

should be assigned a higher priority than R

), both RI

and RE can not distinguish the difference between R

and R

To solve this problem, we can weight probability

and risk impact differently, and (7) can be improved

as (8).

()

IPwI+⋅=

(8)

where,

w is a positive real number and is used to

weight probability and risk impact. Table 6 shows

the functions of

Table 6: Functions of variable w in (8).

Function

Exam

w R

:(0.9, 0.2) R

:(0.2, 0.9)

w>1 I is more important

than P

1.05 RI

=0.924 RI

=0.966

w=1 Both P and I have

the same weight

1.00 RI =0.922 RI

=0.922

0<w<1 P is more important

than I

0.95 RI

=0.920 RI

=0.878

From Table 6, we can find that w can be used to

weight probability and risk impact differently. In

practice, an easy way can be used to determine the

value of

w. Practitioners first assume the weight of

probability,

is 1, and then decide the comparative

weight of risk impact,

, according to the

circumstances of the project, and

w can be derived

from

It’s easy to verify that (8) satisfies constraints 1-4.

Since the introduction of

w only change the range of

I from (0, 1] to (0, w], and does not change the

contours of RI from convex to concave, (8) also

satisfies constraint 5.

According to above analysis, RI not only can

match the risk matrix shown in Fig. 1 well but also

can weight probability and risk impact differently,

whereas RE can not.

To include risk events that offer opportunity, the

definition of RI is enhanced as (9).

() 0

PwIifI

⋅>

−

+⋅ <

⎧

⎪

⎨

⎪

⎩

(9)

4.2 A Case Study

To evaluate RI, we conduct an empirical study on

applying it to a real project. Project A is a project

which enhanced System X to allow customers to

submit documents and related information

electronically via Internet.

The practitioners identified 25 risks after the

project planning and system design phase. Table 7

shows these risks and their probability, impact and

risk level. Both the probability and impact of the risk

are ranked from 0 to 5 (and can be normalized from 0

to 1 as shown in bracket), where a higher probability

value represents a higher chance of occurrence and a

higher impact value represents a higher negative

effect. According to the risk matrix used by the

organization (see Fig. 7), each risk was classified as

Low Risk (L), Medium Low Risk (M-), Medium

Risk (M), Medium High Risk (M+), or High Risk

(H).

In risk prioritization, those risks with the same

probability and impact have the same priority. For

example, Risk 7, 19, 23 and 24 have the same

priority. Thus, we focus on those risks with different

probability and/or impact (Risk 1, 2, 3, 5, 7, 8, 10, 11

and 22) in the following prioritization exercise.

In this project, the practitioners use two rules to

prioritize the risks.

A NEW METHOD AND METRIC FOR QUANTITATIVE RISK ANALYSIS

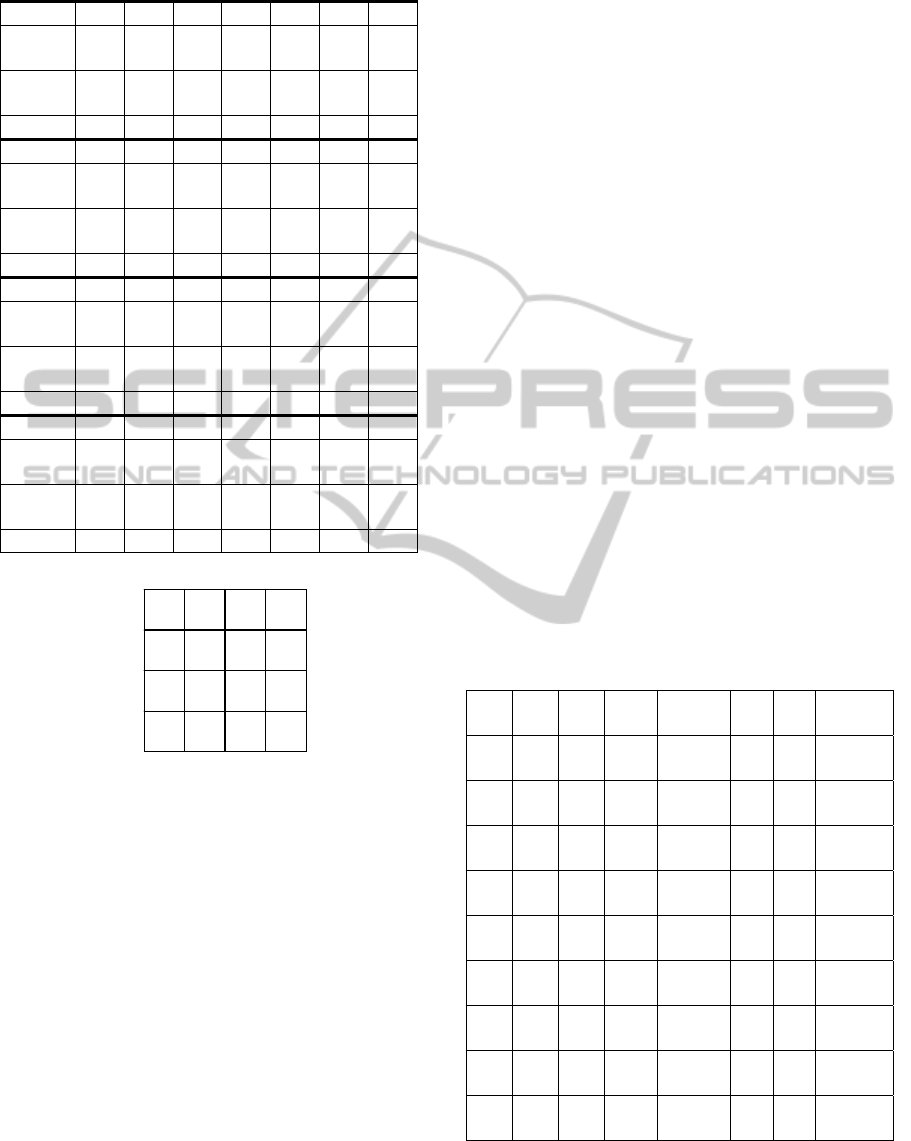
Table 7: Functions of variable w in (8).

Risk No. 1 2 3 4 5 6 7

Probabil

ity

(0.4)

(0.6)

(0.2)

(0.6)

(0.2)

(0.4)

Impact

(0.8)

(0.6)

(0.8)

(0.6)

Level M+ H M- H M M- M

Risk No. 8 9 10 11 12 13 14

Probabil

ity

(0.6)

(0.4)

(0.8)

(0.6)

Impact

(0.6)

(0.8)

(0.6)

(0.8)

(0.6)

Level M+ M+ H H H H M+

Risk No. 15 16 17 18 19 20 21

Probabil

ity

(0.6)

(0.4)

(0.8)

(0.6)

(0.4)

(0.8)

(0.6)

Impact

(0.6)

(0.8)

(0.6)

(0.8)

(0.6)

(0.8)

(0.6)

Level M+ M+ H H M H M+

Risk No. 22 23 24 25

Probabil

ity

(0.4)

(0.6)

Impact

(0.4)

(0.6)

(0.8)

Level M- M M H

0 1 2

3 4

act

M M+ H H

M- M M+ H

L M- M M+

L L M- M

Probability

Figure 7: Risk matrix used by the organization.

First, the risk with higher risk level has higher

priority. Second, for any two risks, R

and R

, in the

same risk level, if (P

and I

), or (P

and

), or (P

and I

) then R

has higher priority

than R

, otherwise the risk with higher impact value

has higher priority as the practitioners pointed out

that “impact is usually easier to be estimated than

probability and people trend to put more efforts on

those higher impact risks”. We prioritize Risk 1, 2, 3,

5, 7, 8, 10, 11 and 22 according to these two rules.

The results are shown in column 5 of Table 8 and this

prioritized list can serve as “standard list” in the

evaluation of RI. Note that the lower priority value

indicates higher priority.

We also compute RE, RI and RI (

w=1.05) with

normalized probability and impact value and

prioritize the risks respectively. The RE, RI and RI

(w=1.05) values of the risks and the priority values

which derived from RE, RI and RI (

w=1.05)

respectively are shown in column 6-8 of Table 8.

Note that priority values are shown in bracket.

In this project, we can find that RE has more

conflicts with the “standard list” than RI. From Table

8, it is easy to find that RI better match the “standard

list” than RE, and RI (

w=1.05) better match the

“standard list” than RI. First, the RE does not

correctly prioritize the risks in different risk levels for

certain cases whereas RI does. For example, Risk 22

with M- risk level should have lower priority than

Risk 5. RE wrongly give them the same priority,

however RI and RI (

w=1.05) prioritize them correctly.

Second, for the risks in the same risk level, RE does

not correctly prioritize them in some cases. For

example, Risk 1 should have higher priority than

Risk 8, and Risk 5 should also has higher priority

than Risk 7. RE wrongly prioritize them, but RI and

RI (

w=1.05) could prioritize them correctly. Further,

in this project, the practitioners view the impact more

important than the probability. Then the RI with w>1

could satisfy the need of the practitioners to a greater

degree. We can find that RI (

w=1.05) could

distinguish Risk 2 and Risk 11, whereas both RE and

RI can not. According to above discussion, we can

draw a conclusion that, in this project, RI is better

than RE in risk prioritization.

Table 8: Priority, RE and RI of 9 risks.

Risk

No.

P I Level Priority RE RI

(w=1.05)

10 4

(0.8)

H 1

0.64

(1)

1.13

(1)

1.16

(1)

2 3

(0.6)

(0.8)

H 2

0.48

(2)

1.03

(2)

11 4

(0.8)

(0.6)

H 3

0.48

(2)

1.02

(3)

1 2

(0.4)

(0.8)

M+ 4

0.32

(5)

0.89

(4)

0.93

(4)

8 3

(0.6)

M+ 5

0.36

(4)

0.85

(5)

0.87

(5)

5 1

(0.2)

(0.8)

M 6

0.16

(7)

0.82

(6)

0.86

(6)

7 2

(0.4)

(0.6)

M 7

0.24

(6)

0.72

(7)

0.75

(7)

3 1

(0.2)

(0.6)

M- 8

0.12

(9)

0.63

(8)

0.66

(8)

22 2

(0.4)

M- 9

0.16

(7)

0.57

(9)

0.58

(9)

Note that RI is not always better than RE. For

example, if there is a Risk26:(4, 1) in the project. It

should have lower priority than Risk5 and Risk7, that

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

is, Risk5> Risk7> Risk26. RE prioritize them as

Risk7> Risk5= Risk26, RI prioritize them as Risk5=

Risk26> Risk7, and RI (

w=1.05) prioritize them as

Risk5> Risk26> Risk7. In this case, none of the

metrics can prioritize the risks correctly.

5 CONCLUSIONS

In this paper, we identified the research gap in

measuring risk impact and some problems with the

common indicator RE for prioritizing risks. To

bridge this gap, we propose a method for measuring

risk impact by using AHP. Then, we propose risk

intensity (RI) to prioritize the risks of a project.

According to our analysis in section III and IV, our

method for assessing risk impact would be more

accurate than other existing methods and RI is better

than RE in prioritizing risks.

Our study has some limitations. First, although the

proposed method for assessing risk impact would be

more accurate than other methods according to our

analysis, it has not been fully evaluated in practice.

Second, we only evaluate RI in one project. The

usefulness of RI needs to be confirmed by applying it

to more projects in the future. We plan to evaluate

the validity of our method for assessing risk impact

and the practical usage of RI with more real-life

projects in the near future.

REFERENCES

Bhushan, N. and Rai, K., 2004. Strategic Decision Making:

Applying the Analytic Hierarchy Process. London,

Springer.

Boehm, B., 1989. Software Risk management, IEEE

Computer Society Press.

Boehm, B., 1991. “Software risk management: principles

and practices”, IEEE software, Vol.8, No.1, pp.32-41.

Cox, L. A., et al, 2005. Huber, “Some limitations of

qualitative risk rating systems”, Risk Analysis, Vol.25

No.3, pp.651-662.

Cox, L. A. 2008, “What's Wrong with Risk Matrices?”,

Risk Analysis, Vol.28, No.2, pp.497-512.

Ferguson, R. W., 2004, “A project risk metric”, CrossTalk:

The Journal of Defense Software Engineering, Vol.17,

No.4, pp.12-15.

Forman, E. H., and Gass, S. I., 2001. "The analytical

hierarchy process-an exposition", Operations

Research, Vol.49, No.4, pp.469-486.

Gluch, D. P., 1994. “A Construct for Describing Software

Development Risks”, SEI Technical Report

CMU/SEI-94-TR-14, SEI, Pittsburgh, PA.

Jones, C., 1996. Patterns of Software Failure and Success,

Boston, MA: International Thompson Computer Press.

Kähkönen, K., 2001. “Integration of Risk and Opportunity

Thinking in Projects”, Presented in Proceedings of 4

European Project management Conference, London,

Jun, PMI Europe 2001.

Kerzner, H., 2006. Project management: a systems

approach to planning, scheduling, and controlling, 9

edition, Hoboken, N.J.

Lipovetsky, S. and Tishler, A., 1994. “Linear methods in

multimode data analysis for decision making”,

Computers and Operations Research, Vol.21, No.2,

pp.169-183.

Lipovetsky, S., 1996. “The synthetic hierarchy method: an

optimizing approach to obtaining priorities in the

AHP”, European Journal of Operational Research, 93,

pp.550-569.

Mcmanus, J., 2004. Risk management in Software

Development Projects, Elsevier, Burlington, MA.

Pandian, C. R., 2007. Applied software risk management:

a guide for software project managers, Auerbach,

Boca Raton, Fla.

PMI, 2008. A guide to the project management body of

knowledge, 4

edition, Project management Institute,

Newtown, PA.

Saaty, T. L., 1994. Fundamentals of Decision Making and

Priority Theory with Analytic Hierarchy Process.

Pittsburgh, RWS.

Saaty, T. L., 2008. "Relative Measurement and its

Generalization in Decision Making: Why Pairwise

Comparisons are Central in Mathematics for the

Measurement of Intangible Factors - The Analytic

Hierarchy/Network Process", RACSAM, Vol.102, No.2,

pp.251-318.

Sherer, S., 2004. “Managing risk beyond the control of IS

managers: the role of business management”,

Proceedings of 37

Hawaii International Conference

on System Sciences, Hawaii, Track 8.

White, B. E., 2006. “Enterprise Opportunity and Risk”,

INCOSE 2006 Symposium Proceedings, Orlando.

A NEW METHOD AND METRIC FOR QUANTITATIVE RISK ANALYSIS