
THE CLASSIFICATION OF TIME SERIES UNDER THE
INFLUENCE OF SCALED NOISE
P. Kroha and K. Kr¨ober
Department of Computer Science, University of Technology Chemnitz, 09107, Chemnitz, Germany
Keywords:
Classification, Market time series, Fractal analysis, Fuzzy technology, Stocks, Market behavior.
Abstract:
In this paper, we propose an improvement of a method for market time series’ classification based on fuzzy
and fractal technology. Usually, the older values of time series will be cut off at a specific time point. We
investigated the influence of the fractal features on the classification result. We compared a normal time series
representation, a representation having a smaller box dimension (achieved by exponential smoothing), and a
representation having a greater box dimension (achieved by addind scaled noise). We used different types of
noises and scales to improve the classification result. Our application concerns time series of stock prices. The
market performance of those approaches is analyzed, discussed, and compared with the system without the
scaled noise component.
1 INTRODUCTION
There are two market hypotheses - the efficient mar-
kets and the hypothesis of inefficient markets. The
hypothesisof efficient markets states that the informa-
tion obtained in the time series describing the stock
prices in the past is worthless to prediction because
the complete information from the past is already
fully evaluated, and contained in the last price value.
The hypothesis of inefficient markets says that there
are some influences not completely evaluated, and re-
spected in the last price, and that these factors can be
used for prediction.
Since the beginning of stock trading, traders and
investors try to predict markets. One group of them
uses technical analysis that developed strategies to
analyse the behaviour of charts by means of techni-
cal indicators (e.g. moving average) and react ac-
cordingly, e.g. Turtle Trading (Faith, 2007). The
other group uses fundamental analysis that developed
strategies based on the economic data of companies
and markets, e.g. Value Investing (Graham, 2006).
We do not try to predict the markets. Our research
hypothesis is based on the hypothesis of inefficient
markets and states that it is possible to classify se-
curities in such classes that some of them have sta-
tistically more chances to profit in the current mar-
ket situation than the others. In our previous research
(Kroha and Lauschke, 2010), we implemented a sys-
tem based on fuzzy and fractal technology that sup-
ported our hypothesis stated above. Fuzzy clustering
and the Takagi-Sugeno inference method have been
used for processing of fractal features of time series.
In this paper, we investigate the influence of time
series fractal features to the classification and describe
the implemented component. We analyze possibili-
ties of this method and compare it with the properties
of processes without this component by their average
performance.
The paper is structured as follows. In Section
2, we discuss the related works. Section 3 explains
shortly the concept of the fuzzy and fractal classifier.
Sections 4 and 5 present why and how we extended
our previous system by different methods of noise
generation and exponential smoothing, and how we
scaled them. Experiments and data used are described
in Section 6. The evaluation and results are given in
Section 7 where we analyze all the approachesregard-
ing their market performance. Finally, we conclude in
Section 8.
2 RELATED WORKS
This paper introduces and investigates a method of
changing fractal features of time series added to ideas
published in our previouspaper (Kroha and Lauschke,
334
Kroha P. and Kröber K..
THE CLASSIFICATION OF TIME SERIES UNDER THE INFLUENCE OF SCALED NOISE.
DOI: 10.5220/0003442903340340
In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 334-340
ISBN: 978-989-8425-77-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

2010) that explained also advantages of fuzzy and
fractal methods in comparizon to traditional methods.
A simple fractal system was published by Castillo
(Castillo and Melin, 2007). Compared to our sys-
tem, it uses a normal distribution of price differences
and does not use any changing of fractal features. In
our previous paper (Kroha and Lauschke, 2010), we
showed that the price differences are not normally dis-
tributed. Unfortunately, a direct comparison between
the two systems is impossible, because Castillo’s and
our system use different test environments (Castillo
and Melin, 2007).
Concerning fuzzy technology, there exist several
other applications of Takagi-Sugeno inference for
time series prediction. For example, the work of An-
dreu and Angelov (Andreu and Angelov, 2010), who
proposed an evolving Takagi-Sugeno algorithm for
time series prediction of NN GCI datasets. NN GCI
is a competition of classification and prediction al-
gorithms. The key difference (aside from the data
they use), is that they use a different rule generation
method. They did not use c-mean clustering but linear
clustering. However, the reason why they used fuzzy
clustering is the same: to achieve data-based rule gen-
eration and to avoid static, upfront rulesets.
The field of stock market prediction is filled with
hundreds of forecasting methods. Not all of those are
scientific or viable, but there exist several approaches
that are backed exactly. One example is the techni-
cal analysis that has also been tested as one of alter-
natives for generating input parameters for clustering
in our previous paper (Kroha and Lauschke, 2010).
Interestingly, in our experiments described in (Kroha
and Lauschke, 2010), the technical analysis module
performed worse than fractal analysis and the fuzzy
logic modules.
To classify the market type, we used a news-based
approach in (Kroha and Nienhold, 2010). We clas-
sified stock market news stories into good, bad, and
neutral news and used then the ratio of these values
for prediction. We used the same approach in (Kroha
et al., 2010) but using a support vector machine for
the classification.
We did not find any previous works concerning the
fractal dimension changes suitable for classification.
3 FUZZY AND FRACTAL
CLASSIFICATION
In this section, we will only very briefly describe the
fuzzy and fractal features that we used in our sys-
tem (Kroha and Lauschke, 2010) before we introduce
the improvement by changing fractal dimension de-
scribed as our contribution in this paper. Our sys-
tem has the following three components: fractal di-
mension module, c-mean clustering algorithm, and
Takagi-Sugeno fuzzy inference module.
The fractal dimension module calculates the frac-
tal features of time series. They describe how chaotic
a given time series is. There are several ways to define
and calculate the fractal dimension. We used box di-
mension and Hurst coefficient according to their def-
initions in (Mandelbrot, 1983). Details concerning
the fractal features of market can be found in (Peters,
1994) and in (Peters, 1996).
In addition, we had to use a correlation coefficient
with a line to indicate whether the time series values
are going up or down.
A fuzzy classifier uses three main components:
fuzzyfication, fuzzy inference and defuzzyfication.
The number of classes need to be defined.
Fuzzyfication is the process of transforming sharp
input data into fuzzy data using a membership func-
tion. The fuzzyfier determines what kind of cluster
is more probable for a given input value describing
the time series. The clustering algorithm c-mean dy-
namically calculates the membership function for the
fuzzyfication process. As the input of the c-mean
clustering of time series, we used a triple consisting of
box dimension, Hurst coefficient, and correlation co-
efficient as mentioned above. Futher, it prepares data
for generation inferrence rules dynamically. More de-
tails can be obtained from (Castillo and Melin, 2003).
Then, using fuzzy inference according to the dy-
namically generated rules, a prediction value is in-
ferred. The rules are generated dynamically on the
basic of the input data. For this purpose, we used
the Takagi-Sugeno inference method (Kluska, 2009).
This function is valid for a certain dataset, it is, how-
ever, dynamic and individually generated for each
dataset.
To interpret the output prediction value, it will be
defuzzified. In our case, its definition interval is di-
vided on three parts because we classify into three
classes. The prediction value membership to a subin-
terval indicates whether the classified time series will
be associated with the class BUY, SELL, or HOLD.
Time series of the class BUY have more common fea-
tures with time series that were going up in the past,
and time series of the class SELL have more common
features with time series that were going down in the
past under similar conditions. The architecture of our
time series classification system is in Fig. 1.
THE CLASSIFICATION OF TIME SERIES UNDER THE INFLUENCE OF SCALED NOISE
335

Figure 1: Our time series classification system.
3.1 Why Changing Fractal Dimension
Makes Sense
Supposing that a part of the future can be predicted
based on the history. Then the question is how much
of the history should be use to predict the future, and
whether all parts of the time series should have the
same weighting.
In stock market forecasting, there are many traders
who believe that older data is not as important as
newer data, e.g. daytraders. Other traders use some
indicators based on long time intervals, e.g. 20-day or
200-day simple moving average. Even though, some
features of a company are durable, many things can
change during 200 days. The administration of a com-
pany may change, its product may become obsolete,
new factories may be built that influence the price of
a product and competition on the market.
The first version of our system was built on the
idea that inside of a specified time interval (we used
30 days for our experiments) each value of the time
series is as important as the other.
Classical methods of technical analysis usually
state a limit of the influence, they cut the influence
sharply (e.g. after 20 days, after 200 days), but all
values in the moving average have the same weight,
i.e. the same influence, like in the case of the simple
moving average.
There are also others models known, like
weighted moving average (more recent values are
more heavily weighted). The commonest type of
weighted moving average is exponential moving av-
erage applied as exponential smoothing. Exponen-
tial moving average (values are assigned to expo-
nentially decreasing weights over time) reacts faster
to recent prices and is used for known technical in-
dicator MACD (moving average convergence diver-
gence). Variable moving average is an exponential
moving average that derives its smoothing percentage
based on market volatility. Triangular moving aver-
age is double smoothed, i.e. it is averaged from sim-
ple moving averages. In such a case, investors using
these moving averages in their trading strategies must
have a special strategy for any kind of the moving av-
erage.
However, time is not the only one important fac-
tor. In (Kroha and Reichel, 2007), we classified tex-
tual market news using supervized learning, i.e. an
investor decided during the training phase which of
news stories is a good or bad story. When using
the trained and tested classifier we stated that the ra-
tio of good stock market news to bad stock market
news build a context, e.g. investors are more enthu-
siastic, and has a predictive quality (Kroha and Nien-
hold, 2010). We experimented with time series fractal
features to influence the results of this classification.
To decrease the box dimension we used exponential
smoothing, to increase the box dimension we used
added, scaled noise as we show in the next sections.
4 INCREASING FRACTAL
DIMENSION
Our original idea is to influence the fractal dimension.
To increase it we use noise. The key thoughts behind
this idea are:
• The addition of (random) noise to a part of time
series makes the time series more chaotic, result-
ing in appropriate fractal dimension changes.
• When noise is added to a time series with a very
distinct trend, the trend may penetrate through the
noise.
• Making a decision based on a noisy time series is
harder, therefore the algorithm will decide more
careful when a certain part of the time series is
noisy.
• If we now selectively noisify parts of the time se-
ries, e.g. the older parts, we enforce careful be-
havior by the algorithm. This selection we called
scaling the noise. It means that the noise ampli-
tude is controlled, scaled by a given function.
Figure 2: White noise.
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
336
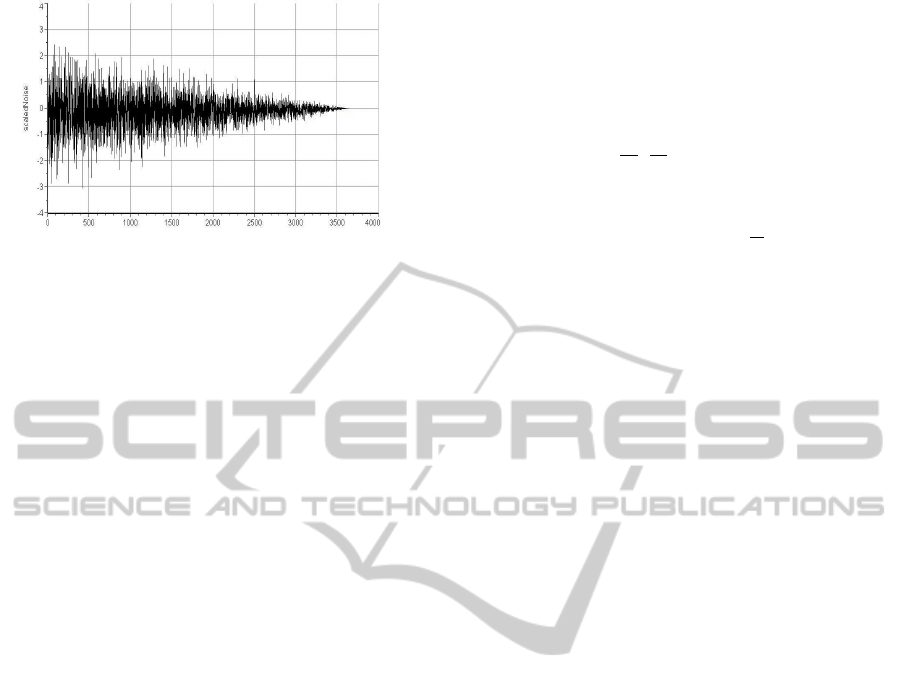
Figure 3: Scaled white noise.
Every noise variant is generated as a sequence
U = (u
1
,u
2
,... ,u
n
). Every scaling variant is gen-
erated as a sequence S = (s
1
,s
2
,... ,s
n
). They both
have the same size n, the size of the original time se-
ries X = (x
1
,x
2
,... ,x
n
) for which they were gener-
ated. Now, we generate a new time series X
′
defined
as (x
1
+ u
1
∗ s
1
,x
2
+ u
2
∗ s
2
,...,x
n
+ u
n
∗ s
n
). In other
words, we scale the noise and add it to the time series.
There exist several different kinds of noise, which
differ by Hurst coefficient. We chose to use white
noise for the first version of our implementation be-
cause it is easy to generate and random. White noise
is a set of uncorrelated random variables with an ex-
pected value of zero and a constant variance. The ran-
dom values should be uniformely distributed. There
are several methods of generating white noise. We
chose to use the Central Limit Theorem (Kuo, 1996)
in our implementation.
The noise is used to influence the fractal calcula-
tions on the data, i.e. we do not influence the data
values. However, we do not want the whole time se-
ries to be noisy, just that parts that follow a certain
(predefined) criteria, e.g. the older parts. Therefore,
as already described above, we had to scale the noise.
We decided to experiment with the noise scaled ac-
cording to linear function, Pareto function, and good
news/bad news function based on results in (Kroha
et al., 2006), (Kroha et al., 2007).
The scaling can be interpreted as a model of in-
fluence probability of historical market prices on the
current price, i.e. the influence of older values weak-
ens accordingly to the scaling function.
Linear scaling takes the form of a linear function
with a dynamically adjusted gradient. The idea is,
that at the beginning of the time series (at time zero),
the linear function intersects the y-axis at exactly 1.
Precisely at the last point of the time series the lin-
ear function should reach 0. The scales are another
sequence of numbers with the same amount of data
points as the time series itself. The scales are defined
as S = (s
1
,s
2
,...,s
n
) with s
i
= 1− S∗ (1/n)∗ i or s
i
= 0
when the equation results in a number below 0. In the
equation S, there is a constant scaling parameter and
is used to influence the gradient of the linear function.
As basis for the Pareto scaling method, we use the
Pareto probability density function. It can be calcu-
lated as such:
f
x
(x) =
α
x
0
(
x
0
x
)
α+1
,α,x
0
> 0 (1)
α and x
0
are both parameters that can be chosen
freely. The Pareto density function equals 0 for all
x < x
0
. Then at x
0
it has the value of
α
x
0
. Afterwards it
declines rapidly and approaches 0 without ever reach-
ing it. Pareto scales can be heavily customized by
changing both the α and the x
0
parameter. Ideally, the
Pareto scales are fitted for each time series, since this
cannot be done all the time, you need to find parame-
ters that work for all your time series. For example, if
you would want to apply Pareto scales to a number of
time series, each consisting of 30 points, you would
need to set an x
0
in the interval [0,30]. Otherwise,
your Pareto scale values would be always 0 or near
zero.
As already discussed above, we wanted to in-
clude not only time dependent methods of scaling but
methods that use prefabricated prediction results from
other systems. As an example, we used our own im-
plemented method - a grammar-based prediction de-
rived from good and bad market news described in
(Kroha and Reichel, 2007).
5 DECREASING FRACTAL
DIMENSION
In the previous part, we described how to increase the
fractal dimension. In this section, we describe how to
decrease fractal dimension.
Exponential smoothing is a well known weighted
moving average for time series analysis. It is used
either for smoothing a time series to appear more aes-
thetically pleasing, or as a simple form of prediction,
based on past samples.
The calculation of a smoothened time series for an
input time series X = (x
1
,... ,x
n
) is done as such:
y
1
= x
1
(2)
y
t
= αx
t
+ (1− α) ∗ y
t− 1
,t > 1 (3)
α is the smoothing factor. If it is 1, each point of
the smoothened time series does not include informa-
tion of the past. When the value is near 0, the past
information is included to the fullest.
The basic idea of exponential smoothing and our
concept of changing fractal features of a time se-
ries using noise is similar. The smoothing process
THE CLASSIFICATION OF TIME SERIES UNDER THE INFLUENCE OF SCALED NOISE
337

Table 1: System without using noise.
variant 1 variant 2 variant 3
Box Dim 1.489 - 1.488
Hurst - 0.418 0.418
correlation 0.288 0.288 0.288
result 2.687 -13.040 0.731
decision 50 0 50
HOLD SELL HOLD
changes fractal features of a curve or a time series.
Older data points are assumed to have an exponen-
tially lesser influence on the future than newer ones
because of the member (1− α)
n
) in the definition. To
present smoothing like an addition of a noise compo-
nent we can imagine that smoothing adds a function
containing ”complementing asperities” to the time se-
ries so that the sum builds a smoothed curve.
6 USED DATA AND
EXPERIMENTAL RESULTS
We used the same input data as used in (Kroha and
Lauschke, 2010) to make it possible to compare the
two systems. This data consists of 53 stocks traded
in Germany. We chose to follow every stock from its
beginning onto the 21.07.2009, the day to which our
data extends. The trading strategy we used is from
our previous work (Kroha and Lauschke, 2010). Ev-
ery 30 days the program analyses this last timespan
(with and without noise) and makes a decision regard-
ing hold, buy or sell. Since our noise-based approach
is experimental, we have to find out the difference to
the noise-free approach.
A calculation for each specific input variable com-
bination (box dimension, Hurst, correlation coeffi-
cient) takes around 20 minutes of computing time, re-
gardless of adding noise or not. We used a PC with the
following features - AMD Athlon Dual Core Proces-
sor 4850e, 2500 MHz (2 cores), 2 GB RAM, SAM-
SUNG SP2504C ATA hard disk.
6.1 Time Series without Changes
To test the existence of a difference, we used the
time series of the Adobe stock from 19.2.2001 to
30.3.2001, amounting to exactly 30 different data
points. There are three variants of possible input pa-
rameters. The first variant consists of box dimension
and correlation coefficient. The second variant con-
sists of Hurst Coefficient and correlation coefficient.
The third variant uses box dimension, Hurst coeffi-
cient and the correlation coefficient.
Table 1 shows the input values of all three com-
binations obtained from the fractal method as well
as the y
res
decision value calculated by the Takagi-
Sugeno fuzzy inference for the Adobe time series.
The discrete decision value is calculated using a sim-
ple border test introduced in (Kroha and Lauschke,
2010). This means that in this particular case 1 all
variants suggest to hold, except the Hurst correlation
variant, which suggests to sell.
6.2 Increased Fractal Dimension
Now, we have to find out what influence the addi-
tion of timescaled noise has on the parameters of
the process. The following experiment was done us-
ing scaled linear noise with a gradient of -2 over
the whole time series. That means at the beginning
the noise is the strongest and afterwards it declines
rapidly. At the middle point of the time series, the
noise stops completely. The decisions were SELL
(Variant 1), HOLD (Variant 2), and HOLD (Variant
3). The box dimension was shifted from 1.5 to 1.7. A
value near 2 means, the time series behaves randomly.
As expected, the addition of timescaled noise (which
is random) makes the time series more random. The
correlation coefficient however, rises from 0.3 to 0.7
and therefore indicates a positive trend. The Hurst
Exponent is rather indecisive with a value near 0.5.
In the case of the news scaled white noise, the de-
cisions were HOLD (Variant 1), BUY (Variant 2), and
HOLD (Variant 3). This is the only test where the al-
gorithm actually proposed to buy stocks.
6.3 Decreased Fractal Dimension
The next experiment used an exponentially smoothed
time series, whereas α = 0.3. As expected, the
Hurst value changed in the direction of trends. Al-
though it is not a big change, the low smoothing fac-
tor only took out the sharpest edges of the time se-
ries. The Box Dimension changed accordingly. It de-
creased, which implies that the new time series con-
tains clearer trends. Correlation became more neu-
tral, it did not detect any positive or negative trends.
As one would expect, smoothing the time series takes
out some of the chaos, this can clearly be seen in the
newly calculated input values. The decisions were
HOLD (Variant 1), SELL (Variant 2), and HOLD
(Variant 3).
On the examples above, we just showed that the
decision signals change when applying scaled noise
on a time series of security prices. The next question
is whether it is in a common case of a time series the
same and how much performance, i.e. profit, it brings.
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
338
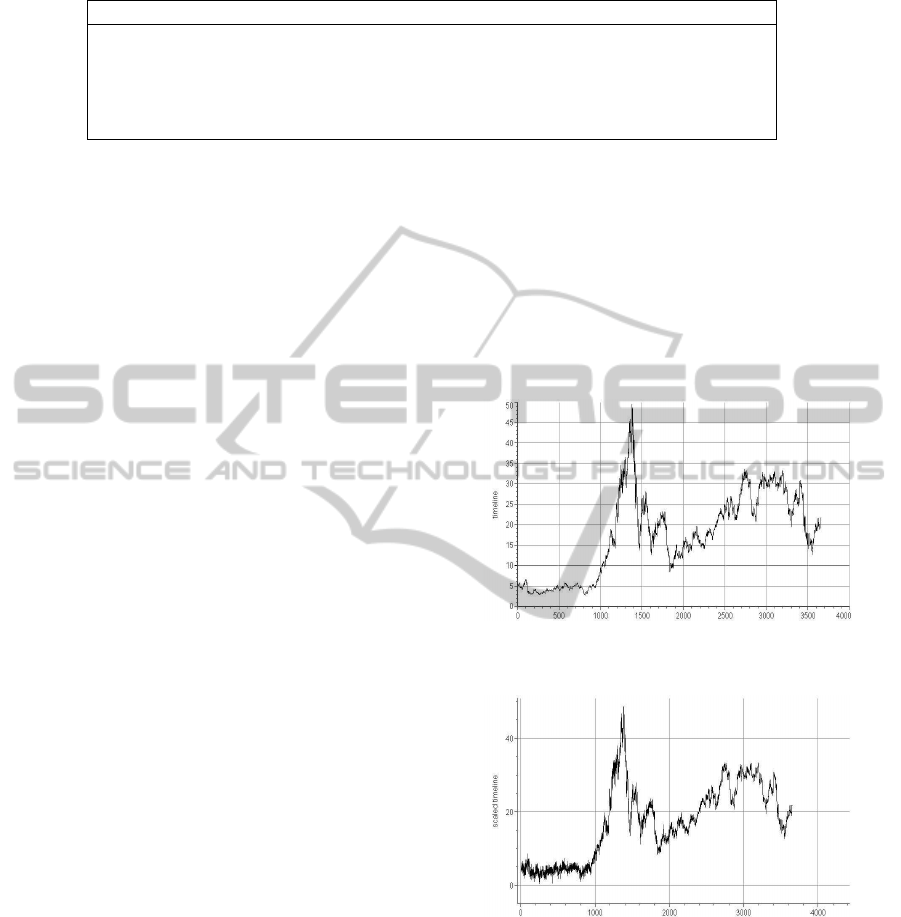
Table 2: Ranked results according to profit earned.
rank profit noise scale
1 175,537 exponential smoothing linear(factor 1)
2 174,386 none none - original values
3 167,688 white noise linear(factor 1)
4 142,388 white noise news controlled scale
5 112,040 none none - 10 day’s simple moving average
This topic is discussed in the next section.
7 EVALUATION AND ACHIEVED
RESULTS
To decide whether the change of fractal features has
brought any significant changes in decision we have
to test how both methods perform in trading. Our ex-
periments and results are shown in this section.
When we try to classify the quality of a prediction
we have to think about the average case. The diffi-
culty is that in the stock market there is no average
situation against which a prediction algorithm could
be measured. So, we decided to process time series of
each of the 53 individual stocks and compare, which
approach performs best. We implemented a simula-
tion in which 10.000 Euros ares invested into each of
the 53 stocks at the beginning and we evaluate the re-
sults at the end of the time interval of 30 days.
The results of the test using the process without
noise show that it was profitable in sum. The variant 1
of input parameters (box dimension/correlation) was
the most profitable with a gain of 174,386. We ex-
perimented also with values of 10 day’s simple mov-
ing average. It leads to practically the same box di-
mension in each part of the time series, but its per-
formance is much worse 2 probably because of the
delay.
Increasing fractal dimension by a linear scaling
factor of 1 for linear scaled noise, the variant 3 ( box
dimension/Hurst/correlation) was the most profitable
one, but with a gain only 167,688. Using factor 2, the
highest gain was 133,065. Using Pareto function (for
α = 0.3 and x
0
= 15), the highest gain was 128,395
for the variant 1. The experiment with news scaled
noise produced a good result, with a gain of roughly
142,000, it ranked 5 in the result comparison (see Ta-
ble 2). This shows that third party scales can be im-
plemented and used in our system.
Decreasing fractal dimension by exponential
smoothing without scaling was less promising. The
method achieved an (only average) gain of rougly
40000 in the first two methods. Using box dimen-
sion, Hurst and correlation resulted in a loss of 1500.
Exponential smoothing seemed at first sight as a good
method to include time information into the fractal
analysis, but performed subpar. We did another test
with linear scaled exponential smoothing. This exper-
iment showed a vast improvement over the unscaled
smoothing. With a gain of rougly 175,000 using vari-
ant 3 (box dimension/Hurst/correlation), this method
performed better than the original approach, if only
by a small amount.
Figure 4: Original time line - Adobe.
Figure 5: Time line with added noise - Adobe.
When dealing with the stock market, there were
several experiments that dealt with choosing stocks
randomly, e.g. using a monkey as an investor. We
also tried this approach to simulate randome deci-
sions. We did several tests, each with other random
number generator seeds. We found that the random
decision achieved a loss of 77,975 under the same
conditions. This means that it vastly underperformed
the fractal analysis approaches. None of the fractal
analysis methods made as big as a loss as the random
method.
THE CLASSIFICATION OF TIME SERIES UNDER THE INFLUENCE OF SCALED NOISE
339
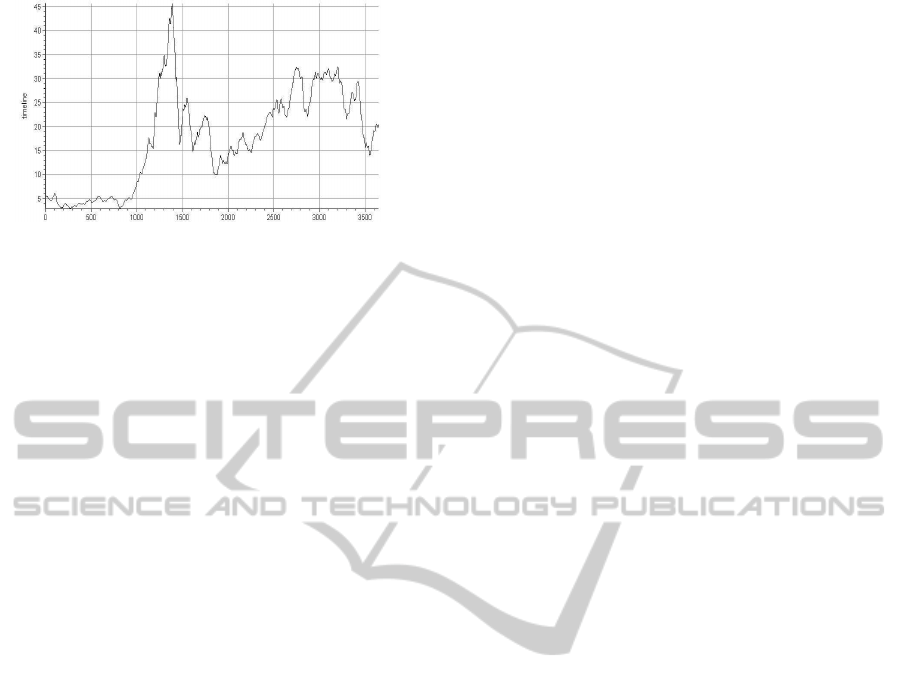
Figure 6: Smoothened time line - Adobe.
8 CONCLUSIONS
As we can see in Table 2, the experiment based on ex-
ponential linear scaled exponential smoothing made
a greater profit than the original approach without
scaled noise, i.e. decreasing fractal dimension influ-
enced the classification positively. In all cases, the
best combination of input values was used. It has
to be mentioned that real life trading has some ad-
ditional aspects. First, investors usually avoid some
stocks that do not have a promissing performance, so
they are not investing in all stocks and may achieve
statistically better performance. Second, we did not
involve fees and taxes paid when trading. This aspect
can worsen the performance very heavily.
However, there are several parameters in the gen-
eration and scaling of noise that can be tuned. For
example, using a time interval of only 20 days, we
obtained much less gain. So, much more experiment-
ing in the future is necessary.
Of course, we are aware of the fact that the pro-
cesses running behing the markets are sometimes
more, sometimes less chaotic, and because of that the
optimization of some features may fail.
Summarized, the answer to the question given in
our hypothesis at the very beginning is: Yes, fractal
dimension decreasing can improve the results at least
in some cases as shown above.
REFERENCES
Andreu, J. and Angelov, P. (2010). Forecasting time-series
for nn gc1 using evolving takagi-sugeno (ets) fuzzy
system with on-line inputs selection. WCCI 2010
IEEE World Congress on Computational Intelligence
CCIB, Barcelona, Spain.
Castillo, O. and Melin, P. (2003). Soft Computing and Frac-
tal Theory for Intelligent Manufacturing. Springer.
Castillo, O. and Melin, P. (2007). Evolutionary design and
applications of hybrid intelligent systems. Interna-
tional Journal of Innovative Computing and Applica-
tions Vol. 1, No. 1.
Faith, C. (2007). The Way of the Turtle: The Secret Methods
that Turned Ordinary People into Legendary Traders.
McGraw-Hill.
Graham, A. (2006). The Intelligent Investor. Collins Busi-
ness Essentials.
Kluska, J. (2009). Analytical Methods in Fuzzy Modeling
and Control. Springer.
Kroha, P., Baeza-Yates, R., and Krellner, B. (2006).
Text mining of business news for forecasting. In
In: Proceedings of 17th International Conference
DEXA’2006, Workshop on Theory and Applications of
Knowledge Management TAKMA’2006, pp. 171-175.
IEEE Computer Society.
Kroha, P., Kroeber, K., and Janetzko, R. (2010). Classifi-
cation of stock market news using support vector ma-
chines. Proceedings of ICSOFT2010 - International
Conference of Software and Data Technologies, Vol.
1, pp. 331-336.
Kroha, P. and Lauschke, M. (2010). Using fuzzy and fractal
methods for analyzing market time series. Proceed-
ings of the International Conference of Fuzzy Com-
puting ICFC’2010, pp. 85-92.
Kroha, P. and Nienhold, R. (2010). Classification of market
news and prediction of market trends. Proceedings of
the International Conference of Enterprise Informa-
tion Systems ICEIS’2010, Vol. 2, pp. 187-192.
Kroha, P. and Reichel, T. (2007). Using grammars
for text classification. Proceedings of the Interna-
tional Conference of Enterprise Information Systems
ICEIS’2007, Vol. Artificial Intelligence and Decision
Support Systems, pp. 259-264.
Kroha, P., Reichel, T., and Krellner, B. (2007). Text mining
for indication of changes in long-term market trends.
In In: Tochtermann, K., Maurer, H. (Eds.): Proceed-
ings of I-KNOW’07 7th International Conference on
Knowledge Management as part of TRIPLE-I 2007,
Journal of Universal Computer Science, pp. 424-431.
Kuo, H.-H. (1996). White Noise Distribution Theory. CRC
Press.
Mandelbrot, B. (1983). Fractal Geometry of Nature. W.H.
Freeman, New York.
Peters, E. (1994). Fractal Market Analysis. Wiley.
Peters, E. (1996). Chaos and Order in the Capital Markets.
Wiley.
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
340
