OBSTACLE AVOIDANCE WITH SIMULTANEOUS

TRANSLATIONAL AND ROTATIONAL MOTION CONTROL

FOR AUTONOMOUS MOBILE ROBOT

Masaki Takahashi, Takafumi Suzuki, Tetsuya Matsumura and Ayanori Yorozu

Dept. of System Design Engineering, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama 223-8522, Japan

Keywords: Service Robot, Obstacle Avoidance, Omni-directional Platform, Fuzzy Potential Method.

Abstract: This paper presents a real-time collision avoidance method with simultaneous control of both translational

and rotational motion with consideration of a robot width for an autonomous omni-directional mobile robot.

In the method, to take into consideration the robot’s size, a wide robot is regarded as a capsule-shaped case

not a circle. With the proposed method, the wide robot can decide the direction of translational motion to

avoid obstacles safely. In addition, the robot can decide the direction of the rotational motion in real time

according to the situation to perform smooth motion. As an example of design method of the proposed

method, novel control method based on the fuzzy potential method is proposed. To verify its effectiveness,

several simulations and experiments using a real robot are carried out.

1 INTRODUCTION

Various obstacle avoidance methods and their

availabilities for mobile robots have described (Du,

2007)-(Dieter, 1997). Most of these studies regard

the robots as points or circles and discuss control

methods of translational motion. In these studies, a

non-circle robot is regarded as a circle robot with

consideration of maximum size of the robot. The

effectiveness of avoiding obstacles by this approach

has been confirmed. However, depending on the

shape of the robot, this approach reduces and wastes

available free space and can decrease the possibility

that the robot reaches the goal. If wide robots, which

are horizontally long, are regarded as circles in

accordance with conventional approaches, they may

not be able to go between two objects due to the

largest radius of the robot, even if they ought to be

able to go through by using their shortest radius.

This suggests the necessity of a suitable orientation

angle at the moment of avoidance. Consequently, to

enable wide robots to avoid obstacles safely and

efficiently, it is necessary to control not only a

translational motion but also a rotational motion. In

our current research, a wide robot with omni-

directional platforms shown in Figure 1 is

developed.

Several studies have focused on the orientation

angle of the robot (Kavraki, 1995)(Wang and

Chirikjian, 2000). In these studies, by convolving the

robot and the obstacle at every orientation and

constructing the C-space, the suitable orientation

angles of the robot for path planning are decided.

However, these methods require an environmental

map and the studies have not shown the

effectiveness for avoidance of unknown obstacles by

autonomous mobile robots. Therefore, to avoid

unknown obstacles reactively with consideration of

the orientation angle, wide robots need an algorithm

that can decide the orientation angle and rotational

velocity command in real time based on current

obstacle information.

This study proposes a control method of both

translational and rotational motion with

consideration of a robot width in order to achieve a

smooth motion. With the proposed method, the

Figure 1: An autonomous robot for hospital use.

Takahashi M., Suzuki T., Matsumura T. and Yorozu A..

OBSTACLE AVOIDANCE WITH SIMULTANEOUS TRANSLATIONAL AND ROTATIONAL MOTION CONTROL FOR AUTONOMOUS MOBILE ROBOT.

DOI: 10.5220/0003443300050013

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 5-13

ISBN: 978-989-8425-75-1

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

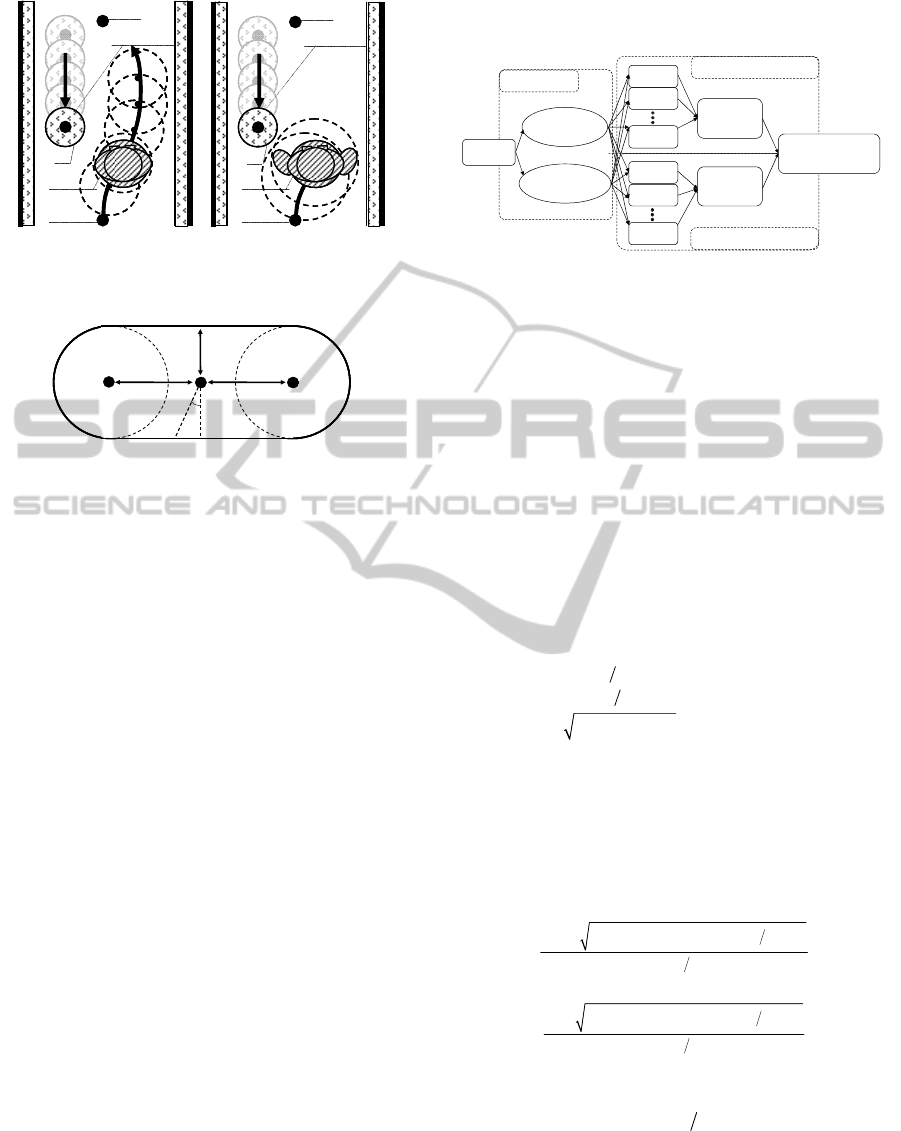
(a) Situation A (b) Situation B

Figure 2: Two robots which are included in respective

circles.

Figure 3: Capsule-shaped case.

orientation angle is controlled easily in real time. To

verify the effectiveness of the proposed method,

several simulations and experiments using our robot

shown in Figure 1 are carried out.

2 SIMULTANEOUS

TRANSLATIONAL

AND ROTATIONAL MOTION

CONTROL

2.1 Problem for Solution

There are various non-circle robots. These are

vertically long robots, or wide robots. These robots

have two arms mounted on a torso with wheels so

these robots can be used for mobility, manipulation,

whole-body activities, and human-robot interaction

(Ambrose, 2004)(Takahashi, 2009). For these wide

robots, conventional obstacle avoidance methods are

incompatible because they regard the robot as a point

or a circle. We are developing a wide robot with a

torso, two arms and a head shown in Figure 1. It not

only moves indoors but also communicates and

interacts with humans through gestures or speech.

When the robot opens one or both of its arms

slightly, as shown in Figure 2(b), it becomes

increasingly difficult to apply conventional obstacle

avoidance methods. If these wide robots are regarded

as circles in accordance with conventional

approaches, it may not be possible for them to go

between two obstacles due to the largest radius of

the robot, even if they

Figure 4: Concept of fuzzy potential method using both

translational and rotational motion with an omni-direction

platform.

ought to go through by using their shortest radius. In

this study, a capsule-shaped case is introduced to

make wide robots move smoothly and safely in an

environment with obstacles.

2.2 Design of Capsule-shaped Case

The capsule-shaped case is modeled by two circles

and two lines tangent to the circles as shown in

Figure 3. This closed contour is defined as

()l

with

the origin at the point

()

() ()

cos

Cif

lC if

XYif

φπ

φφ

≤<

⎧

≤<

⎪

=−

≤<

⎨

⎪

≤<

⎪

⎩

≤<

(1)

where

is clockwise from the back direction of the

robot.

arctan( / ), arctan( / ),

La La

CC CC

φπ

=−

arctan( / ), 2 arctan( / )

aRa

CC CC

πφπ

+=−

()X

and

()Y

are calculated as follows.

()

{}

()

{}

()

222

1tan 2

LLLa

RRRa

CCCC

πφ

φφφ

πφ

φφφ

⎧

−− − − + −

⎪

+−

⎪

≤<

⎪

⎨

⎪

+−− + −

⎪

+−

⎪

≤<

⎪

⎩

(2)

(

)

(

)

(

)

tan 2YX

φπφ

−

(3)

In the proposed method,

,and

are decided

in a way that makes wide robot shape fall within the

capsule-shaped case.

Obstacle

Goal

Start

Robot

Obstacle

Goal

Start

Robot

Obstacle

Goal

Start

Robot

Obstacle

Goal

Start

Robot

PMF 1

PMF 2

PMF i

PMF 1

PMF 2

PMF j

Environment

Own condition

Fuzzy

operation

Fuzzy

operation

Omni-directional

drive system

Rotational motion

Translational motion

Information

Sensors

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

Figure 5: Omni-directional platform with wide body.

2.3 Controller Design

Figure 4 shows a concept of the fuzzy potential

method (FPM) that takes into consideration both

translational and rotational motion. In the

conventional FPM (Tsuzaki, 2003), a command

velocity vector that takes into consideration element

actions is decided. Element actions are represented

as potential membership functions (PMFs), and then

they are integrated by means of fuzzy inference. The

horizontal axis of PMF is directions which are from

−

radians measured clockwise from the front

direction of the robot. The vertical axis of PMF is

the grade for the direction. The grade, direction, and

configured maximum and minimum speeds, are used

to calculate the command velocity vector.

In this research, in addition to conventional

approach the PMFs for translational and rotational

motion are designed respectively based not only on

environmental information but also the robot's

condition. Environmental information and the robot's

condition are treated separately and divided into a

translation problem and a rotational problem. Then

the PMFs of each problem are independently

integrated using fuzzy inference. Finally,

translational and rotational velocity commands,

which are calculated by defuzzification of mixed

PMFs, are realized by an omni-directional drive

system, as shown in Figure 5.

2.4 PMF for Translational Motion

2.4.1 PMF for Obstacles

To enable a wide robot to avoid obstacles safely and

efficiently in real time, a concave shaped PMF

(1,2,,)

= "

shown in Figure 7, which takes into

consideration the capsule case, is generated. This

PMF is specified by depth and width, which are

calculated based on the geometrical relation between

an obstacle and the robot as shown in Figure 6. By

Figure 6: Wide robot and obstacle.

Figure 7: Example of PMF for an obstacle

generating a PMF based on the variables

′

, a and

,ro

in Figure 7, it can choose a safe

direction.

222

PQ PQ PP

arccos .

2PQ PQ

OO LO OL

OO LO

⎛⎞

+−

⎜⎟

⋅

⎜⎟

⎝⎠

JJJJJG JJJJJJGJJJJJG

JJJJJJG JJJJJJG

(4)

222

PQ PQ PP

arccos .

2PQ PQ

OO RO OR

OO RO

⎛⎞

+−

⎜⎟

⋅

⎜⎟

⎝⎠

JJJJJG JJJJJJG JJJJJG

JJJJJJG JJJJJJG

(5)

(

)

()

{}

arcsin P Q P Q .

LO LO

LO s s LO

DifD

dDdifD

⎧

⎪

′

⎨

⎪

−−−≥

⎩

JJJJJG JJJJJJG

(6)

(

)

()

{}

arcsin P Q P Q .

RO RO

RO s s RO

DifD

dDdifD

⎧

⎪

′

⎨

⎪

−−−≥

⎩

JJJJJG JJJJJJG

(7)

As a measure to decide how far the robot should

depart from the obstacle,

is defined as the depth of

the concave PMF.

aif

−

(8)

out

Obstacle

′

,ro

Capsule Case

Goal or Subgoal

,rg

Obstacle

′

,ro

Capsule Case

Goal or Subgoal

,rg

grade

direction [rad]

′

,ro

′

−

OBSTACLE AVOIDANCE WITH SIMULTANEOUS TRANSLATIONAL AND ROTATIONAL MOTION CONTROL

FOR AUTONOMOUS MOBILE ROBOT

where

(r ,r )

ro x y

is the current position vector of

the obstacle relative to the robot. If the current

obstacle position is inside a circle with radius

from the robot position, a PMF for obstacle

avoidance is generated.

is decided to ensure a

safe distance.

ao s

DC r d=++

(9)

C is the minimum size of the capsule case,

r and

d denote respectively the radius of the obstacle and

the safe distance.

,ro

is the angle of the direction to

the obstacle relative to the robot.

arctan(r / r ) .

ro y x

(10)

For safe avoidance, the PMF

is generated for

all the obstacles that the robot has detected. Then,

they are all integrated by calculating the logical

product

tt t t

oo o oj

μμ μ μ

=∧∧⋅⋅⋅∧

(11)

By deciding the depth and the base width of the

concave PMF

is generated.

2.4.2 PMF for a Goal

To head to the goal, a triangular PMF

generated, as shown in Figure 8.

is specified by

,and

,rg

. As a measure to decide how close

to the goal the robot should go,

is defined as the

height of the triangular PMF. As a measure to decide

how much the robot can back away from obstacles,

is defined.

reaches the maximum value as

at an angle of the goal direction relative to the

front direction of the robot

,rg

1.0

⎧

⎪

≤

⎨

⎪

⎩

(12)

(

)

01 .

ηη

=≤<

(13)

where

,rd

is an absolute value of the position

vector of the goal relative to the robot.

and

are

constants. If

,rd

is below

is defined. The

robot can decelerate and stop stably.

Figure 8: Example of PMF for a goal.

Figure 9: Example of mixed PMF for translational motion.

2.4.3 Calculation of a Translational

Command Velocity Vector

The proposed method uses fuzzy inference to

calculate the command velocity vector. The PMFs

and

are integrated by fuzzy operation into a

mixed PMF

mix

as shown in Figure 9.

mix

is an

algebraic product of

and

ttt

mix g o

μμ

=∧

(14)

By defuzzifier, a velocity command vector is

calculated as a traveling direction

out

and an

absolute value of the reference speed of the robot

based on the mixed PMF

mix

out

is decided as the

direction that makes the PMF

()

mix

maximum.

Based on

out

v is calculated as follows.

()( )

out mix out max min min

vvvv .

μϕ

=−+

(15)

where

()

mix out

μϕ

is the mixed PMF for translational

motion corresponding to the

out

max

v and

min

v are

respectively the upper and lower limits of the robot

speed.

,rg

−

grade

direction [rad]

out

(

)

mix out

μϕ

−

grade

direction [rad]

′

,ro

,rg

out

(

)

mix out

μϕ

−

grade

direction [rad]

′

,ro

,rg

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

2.5 PMF for Rotational Motion

2.5.1 PMF for Obstacles

To enable a wide robot to decide the appropriate

angle of the direction for obstacle avoidance in real

time, PMF

is generated.

rrr

oec

μμ

=−

(16)

Figure 10: Example of mixed PMF for rotational motion.

is generated based on the distance from the

center of the robot to obstacles corresponding to all

directions, as shown in Figure 10. The relative

distances are obtained with range sensors such as

laser range finder, ultra sonic sensors or infrared

sensors.

is generated based on the capsule case.

()

(

)

μϕ

(17)

The aim of the PMF

is to search for an

orientation angle of the robot that would maximize

the distance between a point on capsule case and

each obstacle by turning the front or back side of the

robot. By using the capsule case, a PMF design can

deal with the width of the robot for rotational motion.

2.5.2 PMF for a Goal

In order to turn the front of the robot toward the goal

direction or the travelling direction if there is no

obstacle to avoid, PMF for a goal is generated as

This shape is decided in same way as

2.5.3 Calculation of a Rotational Command

Velocity

For the rotational motion, like the translational

motion, the rotational command velocity is derived.

The PMFs

and

are integrated by fuzzy

operation into a mixed PMF

mix

, as shown in

Figure 10.

rrr

mix g o

μμμ

=∧

(18)

By defuzzifier, the command velocity is

calculated as a rotational direction

ori

and an

absolute value of the reference speed of the robot.

ori

is decided as the direction

that makes the

following function

()h

minimum.

() ()

mix

h d

ϕζ

μψψ

−

∫

(19)

where

is the parameter to avoid choosing an

uncertainty

caused by, for example, noise on the

sensor data. On the basis of

ori

is calculated.

Table 1: Parameters in numerical simulations.

L 0.4 m W 1.0 m

0.3 m C

0.3 m

0.3 m r

0.3 m

0.3 m D 0.9 m

4.0 m

0.2

1.0 m a

1.0 m/s

max

1.0 rad/s

min

0.0 rad/s

sgn( )

a ori

ωϕ

(20)

where

is design variable.

2.6 Omni-directional Platform

An omni-directional platform was used for the

autonomous mobile robot's motion. The command

velocity vector was realized by four DC motors and

omni wheels.

cos .

r out out

(21)

sin

r out out

(22)

where

out

v and

are respectively command

translational velocity vector and rotational velocity.

cos sin

δδ

⎡⎤

⎢⎥

−

⎢⎥

−−

⎢⎥

⎣⎦

⎢⎥

−

⎢⎥

⎣⎦

(23)

is an angle of gradient for each wheel.

is half

−

grade

direction [rad]

(

)

mix ori

ori

−

grade

direction [rad]

(

)

mix ori

ori

OBSTACLE AVOIDANCE WITH SIMULTANEOUS TRANSLATIONAL AND ROTATIONAL MOTION CONTROL

FOR AUTONOMOUS MOBILE ROBOT

the distance between two diagonal wheels.

is a

command velocity of each

-thi

wheel.

3 SIMULATION RESULTS

To verify the effectiveness of the proposed method,

numerical simulations were carried out. In

simulations, the robot was presumed to be able to

detect obstacles and to have information about the

relative position vector. The measuring range was

assumed to be 4.0 m in all directions. Each

parameter was shown in Table 1.

(a) Situation I.

(b) Situation II.

Figure 11: Simulation results.

(a) Situation I: robot cannot find the direction between the

two obstacles.

(b) Situation II: robot can find the direction between the

two obstacles.

Figure 12: Aspects of mixed PMF for translational motion

in two different situations.

3.1 Performance of Capsule Case

To verify the effectivenesses of using capsule case

by comparing the results of the chosen direction of

robot motion, simulations in two different situations

regarding the orientation angle for a wide robot were

carried out. In the simulations, the positions of the

robot and two obstacles were immobilized at each

point respectively

(1.0 m, 2.0 m) , (1.5 m, 0.5 m) and

(3.0 m, 2.0 m) , as shown in Figure 11.

Table 2: Position coordinates of start and goal points of the

robot and of obstacles.

In situation I shown in Figure 11(a), the

orientation angle of the robot was fixed to

−

radians clockwise from the x-axis on the absolute

coordinates. Therefore the robot faced the goal.

Figure 12(a) shows the mixed PMF

mix

in this

situation. The chosen direction of the robot motion

was calculated as

1.35

−

radians, which was

clockwise from the front direction of the robot, as

shown in Figure 11(a). As a result, the robot chose a

longer route to the goal.

In situation II shown in Figure 11(b), the

orientation angle of the robot was fixed to

radians on the absolute coordinates. In contract to

situation I, the robot did not face the goal. Figure

12(b) shows the mixed PMF

mix

in this situation.

The chosen direction of the robot motion was

calculated as

1.37

radians, which was clockwise

from the front direction of the robot, as shown in

Figure 11(b). As a result, the robot chose a shorter

route with no collision.

These two results showed the effectiveness of the

capsule case and that the wide robot can decide the

direction of translational motion that takes

consideration with the robot's orientation, the goal

position and the obstacle position simultaneously in

real time.

3.2 Obstacle Avoidance

The effectiveness of the proposed method was

verified by comparing two design methods based on

FPM in three situations. In method I, the wide robot

was regarded as a circle with radius 0.6 m. In

0 1.0 2.0 3.0 4.

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

Goal point

Start point

Obstacle

Robot

mixed PMF :

Selected direction

mix

(

)

4 rad

−

0 1.0 2.0 3.0 4.

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

0 1.0 2.0 3.0 4.

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

0 1.0 2.0 3.0 4.

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

Goal point

Start point

Obstacle

Robot

mixed PMF :

Selected direction

mix

(

)

4 rad

−

0000

0 1.0 2.0 3.0 4.0

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

Goal point

Start point

Obstacle

Robot

mixed PMF :

Selected direction

mix

(

)

4 rad

0 1.0 2.0 3.0 4.0

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

0 1.0 2.0 3.0 4.0

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

0 1.0 2.0 3.0 4.0

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

0 1.0 2.0 3.0 4.0

1.0

2.0

3.0

x-coordinate [m]

y-coordinate [m]

Goal point

Start point

Obstacle

Robot

mixed PMF :

Selected direction

mix

(

)

4 rad

−

()

mix out

μϕ

out

direction

[

rad

]

−

()

mix out

μϕ

out

direction

[

rad

]

−

()

mix out

μϕ

out

direction

[

rad

]

−

()

mix out

μϕ

out

direction

[

rad

]

Start [m] Goal [m]

(2.5, 1.8)− (2.5, 1.2)− (2.5,1.2) (2.5,1.8)(0.0,0.0) (8.0,0.0)

(0.0, 2.0)− (11, 2.0)

Obstacles [m]

(0.0, 2.0)− (11, 2.0)

(4.0, 2.0)− (4.0, 1.4)− (4.0,1.0) (4.0,1.6)

123

(4.0, 2.0)− (4.0, 1.4)− (4.0, 0.4) (4.0,1.0)

−

(4.0, 2.2)

(4.0,1.6)

Start [m] Goal [m]

(2.5, 1.8)− (2.5, 1.2)− (2.5,1.2) (2.5,1.8)(0.0,0.0) (8.0,0.0)

(0.0, 2.0)− (11, 2.0)

Obstacles [m]

(0.0, 2.0)− (11, 2.0)

(4.0, 2.0)− (4.0, 1.4)− (4.0,1.0) (4.0,1.6)

123

(4.0, 2.0)− (4.0, 1.4)− (4.0, 0.4) (4.0,1.0)

−

(4.0, 2.2)

(4.0,1.6)

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

method II, the capsule case was used and the width

and rotational motion of the robot were taken into

consideration. The start and goal positions of the

robot and the obstacles are shown in Table 2.

In situation A, the robot with method I did not

succeed in going between two objects. It did not

collide with the obstacles and did not get to the goal

point as shown in Figure 13. On the other hand, in

method II, the capsule case and real-time control

based on FPM were used. As shown in Figure 14,

the robot performed translational and rotational

motion simultaneously in real time and succeeded in

going between two objects. Figure 15 shows the time

history of the orientation angle on the absolute

coordinate of the robot. The robot changed the

orientation angle according to the situations and

succeeded in getting to the goal with the orientation

angle 0 radian by using PMF for rotational motion.

In situation B, the robot with method II did not

succeeded to going between two objects as shown in

Figure 16. The robot found another way and got to

the goal point. On the other hand, as shown in Figure

17, the robot with method II performed translational

and rotational motion simultaneously in real time.

Figure 13: Simulation result of method I in situation A.

Figure 14: Simulation result of method II in situation A.

Figure 15: Orientation angle of the robot with method II in

situation A.

Figure 16: Simulation result of method I in situation B.

Figure 17: Simulation result of method II in situation B.

Figure 18: Orientation angle of the robot with method II in

situation B.

Figure 19: A simulation result in the situation C by using

method II.

Figure 20: Orientation angle of the robot with method II in

situation C.

The time history of the orientation angle on the

absolute coordinates of the robot is shown in Figure 18.

-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

-2.0

-1.0

1.0

2.0

x-coordinate [m]

y-coordinate [m]

Obstacle

Robot : t = 0.0s

Robot : t = 24.7s

Goal point

x [m]

y [m]

-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

-2.0

-1.0

1.0

2.0

x-coordinate [m]

y-coordinate [m]

Obstacle

Robot : t = 0.0s

Robot : t = 24.7s

Goal point

-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

-2.0

-1.0

1.0

2.0

x-coordinate [m]

y-coordinate [m]

Obstacle

Robot : t = 0.0s

Robot : t = 24.7s

-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

-2.0

-1.0

1.0

2.0

x-coordinate [m]

y-coordinate [m]

Obstacle

Robot : t = 0.0s

Robot : t = 24.7s

Goal point

x [m]

y [m]

-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

-2.0

-1.0

1.0

2.0

x-coordinate [m]

y-coordinate [m]

Obstacle

Robot : t = 0.0s Robot : t = 24.7s

x [m]

y [m]

-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

-2.0

-1.0

1.0

2.0

x-coordinate [m]

y-coordinate [m]

Obstacle

Robot : t = 0.0s Robot : t = 24.7s

-1.0 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

-2.0

-1.0

1.0

2.0

x-coordinate [m]

y-coordinate [m]

Obstacle

Robot : t = 0.0s Robot : t = 24.7s

x [m]

y [m]

time

[

]

0 5 10 15 20 25

orientation angle [rad]

−

time

[

]

0 5 10 15 20 25

orientation angle [rad]

−

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

-coordinate

[

]

y-coordinate [m]

Obstacle

Robot : t = 42.2s

: t = 0.0s

Robot

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

-coordinate

[

]

y-coordinate [m]

Obstacle

Robot : t = 42.2s

: t = 0.0s

Robot

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

-coordinate

[

]

y-coordinate [m]

Obstacle

Robot : t = 42.2s

: t = 0.0s

Robot

: t = 0.0s

Robot

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

-coordinate

[

]

y-coordinate [m]

Obstacle

Robot : t = 31.8s

: t = 0.0s

Robot

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

-coordinate

[

]

y-coordinate [m]

Obstacle

Robot : t = 31.8s

: t = 0.0s

Robot

: t = 0.0s

Robot

[

]

[

]

[

]

[

]

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

x [m]

y [m]

Obstacle

Robot : t = 36.7s

: t = 0.0s

Robot

x-coordinate [m]

y-coordinate [m]

-coordinate [m]

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

x [m]

y [m]

Obstacle

Robot : t = 36.7s

: t = 0.0s

Robot

x-coordinate [m]

y-coordinate [m]

-coordinate [m]

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

x [m]

y [m]

Obstacle

Robot : t = 36.7s

: t = 0.0s

Robot

x-coordinate [m]

y-coordinate [m]

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

x [m]

y [m]

Obstacle

Robot : t = 36.7s

: t = 0.0s

Robot

-1 0 1 2 3 4 5 6 7 8 9 10 11 12

-2

-1

x [m]

y [m]

Obstacle

Robot : t = 36.7s

: t = 0.0s

Robot

: t = 0.0s

Robot

x-coordinate [m]

y-coordinate [m]

-coordinate [m]

time [s]

0 5 10 15 20 25

rientation angle [rad]

−

time [s]

0 5 10 15 20 25

rientation angle [rad]

−

OBSTACLE AVOIDANCE WITH SIMULTANEOUS TRANSLATIONAL AND ROTATIONAL MOTION CONTROL

FOR AUTONOMOUS MOBILE ROBOT

In situation C, the robot with method II took its

own size into consideration using the capsule case

and chose a path that did not go between the two

obstacles.

These results showed that motion control without

a capsule case made it difficult for the robot to go

between two objects due to the largest radius of the

robot, even if it would be able to go through by using

its shortest radius. Applying the capsule case to a

wide robot, the robot can decide the orientation

angle according to the situation. As a result, the

robot can get to the goal point smoothly and safely.

Figure 21: Laser sensor and an omni-directional platform

on an autonomous mobile robot.

(a) Front (b) Side (c) Top

Figure 22: Experimental situation.

(a) Method I (b) Method II

Figure 23: Trajectory of the robot.

4 EXPERIMENTAL RESULTS

To verify the performance of the proposed collision

avoidance method to static obstacles, an experiment

using the real robot were carried out. In order to

recognize the environment, as shown in Figure 21,

the robot has external sensors, such as a stereo

camera, laser range finder and ultrasonic sensors.

However, in this research the robot recognizes the

environment using only laser range finder.

(a) (d)

(b) (e)

Figure 24: Experimental result to static human using fuzzy

potential method without PMF for rotational motion

(method I).

(a) (d)

(b) (e)

Figure 25: Experimental result to static human using fuzzy

potential method with PMF for rotational motion (method

II).

LRF

4.0m

0.23m

+120°

‐120°

Omni Wheeled Platform

MKR-003

LRF

4.0m

0.23m

+120°

‐120°

Omni Wheeled Platform

MKR-003

-1.0

0.0

1.0

2.0

3.0

4.0

5.0

6.0

7.0

8.0

-2.0 -1.0 0.0 1.0 2.0

y-coordinate [m]

x-coordinate [m]

-1.0

0.0

1.0

2.0

3.0

4.0

5.0

6.0

7.0

8.0

-2.0 -1.0 0.0 1.0 2.

y-coordinate [m]

x-coordinate [m]

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

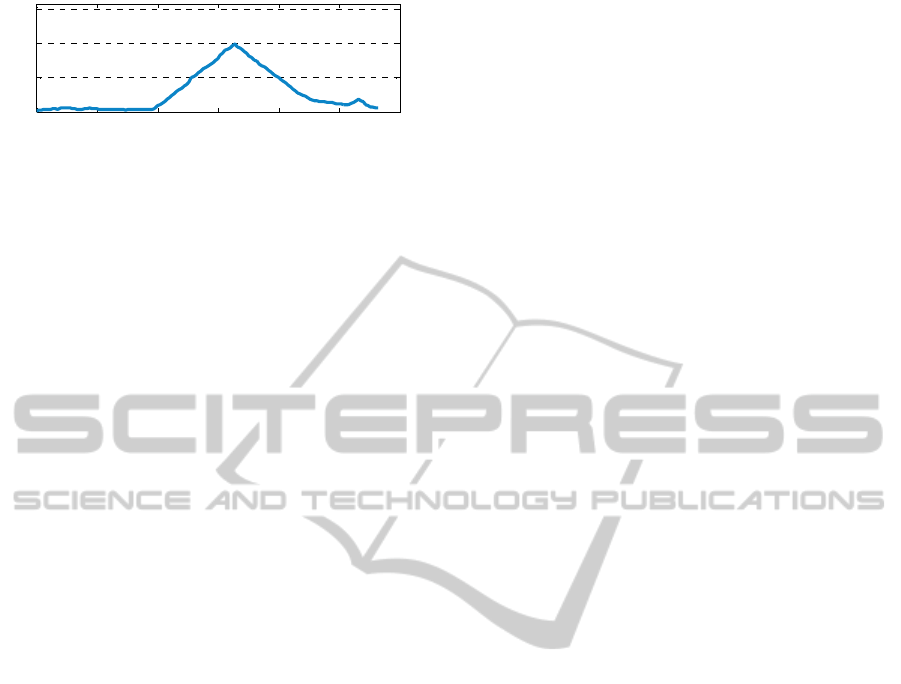
Figure 26: Time history of yaw angle of the robot.

The upper limit of the velocity of the robot was

0.5 m/s. The upper limit of the acceleration of the

robot was 1.0 m/s

. The arm position was set as

shown in Figure 22. Figures 23(a) and 24 showed

that the robot with method I can reach the goal

without colliding with the obstacle. However, the

position of the right arm comes close to the right-

side wall.

On the other hand, it was confirmed in Figures

23(b), 25 and 26 that the robot with the proposed

method (method II) changes the orientation angle of

the robot to keep the safe distance with the right-side

wall and can reach the goal point without colliding

with the obstacle.

5 CONCLUSIONS

In this paper, the real-time collision avoidance

method with simultaneous control of both

translational and rotational motion with

consideration of a robot width for an autonomous

mobile robot, which is horizontally long, has been

proposed. This method used an omni-directional

platform for the drive system and was based on the

fuzzy potential method. The novel design method of

potential membership function, which takes the

robot's size into consideration using the capsule case,

was introduced. With the proposed method, the wide

robot can decide the direction of translational motion

to avoid obstacles safely. In addition, by controlling

rotational motion in real time, the wide robot moves

while keeping a safe distance with surroundings in

narrow space. The effectiveness has been verified by

numerical simulations and experiments. It has been

shown that the proposed method performs

translational and rotational motion simultaneously

according to the situation.

REFERENCES

Kavraki, L., 1995. Computation of Configuration Space

Obstacles Using the Fast Fourier Transform,

IEEE

Trans. on Robotics and Automation

, Vol. 11, No. 3, pp.

408-413.

Wang, Y., Chirikjian, G. S., 2000. A New Potential Field

Method for Robot Path Planning,

Proc. IEEE Int. Conf.

on Robotics and Automation

, San Francisco, CA, pp.

977-982.

Ambrose, R. O., Savely, R. T., Goza, S. M., Strawser, P.,

Diftler, M. A., Spain, I., and Radford, N., 2004.

Mobile manipulation using NASA’s robonaut, Proc.

IEEE ICRA

, pp. 2104-2109.

Du, Z., Qu, D., Yu, F. and Xu, D, 2007. A Hybrid

Approach for Mobile Robot Path Planning in Dynamic

Environments,

Proc. IEEE Int. Conf. on Robotics and

Biomimetics

, pp.1058-1063.

Khatib, O., 1986. Real-time Obstacle Avoidance for

Manipulators and Mobile Robots, Int. J. of Robotics

Research

, Vol.5, No.1, pp.90-98.

Koren, Y., and Borenstein, J., 1991. Potential Field

Methods and Their Inherent Limitations for Mobile

Robot Navigation,

Proc. IEEE Int. Conf. on Robotics

and Automation

, pp.1398-1404.

Borenstein, J., Koren, Y. , 1989. Real-Time Obstacle

Avoidance for Fast Mobile Robots, IEEE Trans. on

Systems, Man, and Cybernetics

, Vol.19, No.5,

pp.1179-1187.

Borenstein, J., Koren, Y., 1991. The Vector Field

Histogram Fast Obstacle Avoidance for Mobile Robots,

IEEE Trans. on Robotics and Automation, Vol.7, No.3,

pp.278-288.

Lumelsky, V. J., Cheung, E. , 1993. Real Time Obstacle

Collistion Avoidance in Teleoperated Whole Sensitive

Robot Arm Manipulators, IEEE Trans. Systems, Man,

and Cybernetics

, Vol.23, No.1, pp.194-203.

Borenstein, J., Koren, Y., 1991. The Vector Field

Histogram Fast Obstacle Avoidance for Mobile Robots,

IEEE Trans. on Robotics and Automation, Vol.7, No.3,

pp.278-288.

Dieter, F., Wolfram, B., Sebastian, T., 1997. The Dynamic

Window Approach to Collision Avoidance,

IEEE

Robotics and Automation

, Vol. 4, No. 1, pp.1-23.

Tsuzaki, R., Yoshida, K., 2003. Motion Control Based on

Fuzzy Potential Method for Autonomous Mobile

Robot with Omnidirectional Vision”.

Journal of the

Robotics Society of Japan

, Vol.21, No.6, pp.656-662.

Takahashi, M., Suzuki, T., 2009. Multi Scale Moving

Control Method for Autonomous Omni-directional

Mobile Robot,

Proc. of the 6th Int. Conf. on

Informatics in Control, Automation and Robotics

0 5 10 15 20 25 30

Time [s]

Yaw angle [rad]

OBSTACLE AVOIDANCE WITH SIMULTANEOUS TRANSLATIONAL AND ROTATIONAL MOTION CONTROL

FOR AUTONOMOUS MOBILE ROBOT