
MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED
MULTIUSER MIMO-OFDM SYSTEMS
Sebastian Aust
1
, Andreas Ahrens
1
and C´esar Benavente-Peces
2
1
Hochschule Wismar, University of Technology, Business and Design, Philipp-M¨uller-Straße 14, 23966 Wismar, Germany
2
Universidad Polit´ecnica de Madrid, Ctra. Valencia. km. 7, 28031 Madrid, Spain
Keywords:
Multiple-Input Multiple-Output System, Orthogonal Frequency Division Multiplexing, Singular-Value
Decomposition, Bit Allocation, Power Allocation, Wireless Transmission.
Abstract:
In order to comply with the demand on increasing available data rates in particular in wireless technologies,
systems with multiple transmit and receive antennas, also called MIMO (multiple-input multiple-output) sys-
tems, have become indispensable for future generations of wireless systems. Due to the strongly increasing
demand in high-data rate transmission systems, frequency non-selective MIMO links have reached a state of
maturity and frequency selective MIMO links are in the focus of interest. In this field, the combination of
MIMO transmission and OFDM (orthogonal frequency division multiplexing) can be considered as an es-
sential part of fulfilling the requirements of future generations of wireless systems. However, single-user
scenarios have reached a state of maturity. By contrast multiple users’ scenarios require substantial further
research, where in comparison to ZF (zero-forcing) multiuser transmission techniques, the individual user’s
channel characteristics are taken into consideration in this contribution. The performed joint optimization of
the number of activated MIMO layers and the number of transmitted bits per subcarrier along with the appro-
priate allocation of the transmit power shows that not necessarily all user-specific MIMO layers per subcarrier
have to be activated in order to minimize the overall BER under the constraint of a given fixed data throughput.
1 INTRODUCTION
The requirements for transmission capacity for
speech, data and multimedia information will proba-
bly increase continuously in the future. With the lim-
itation of available resources such as transmit power
or bandwidth, the demand to increase the spectral ef-
ficiency of future transmission systems is clearly rec-
ognizable.
Multicarrier transmission such as OFDM (orthog-
onal frequency division multiplexing) represents a
suitable method for the digital signal transmission
over linear distorting channels (Bingham, 2000), (van
Nee and Prasad, 2000), (Hwang et al., 2003). The
available transmission bandwidth is decomposed into
a number of narrowband channels in which data
streams are transmitted with reduced speed. Further-
more, it offers a great spectral efficiency which is a re-
quirement in current communication systems to trans-
mit at high data rates over band limited channels, spe-
cially those aimed at transmitting multimedia content.
However, in order to comply with the demand on
increasing available data rates in particular in wire-
less technologies, systems with multiple transmit and
receive antennas, also called MIMO (multiple-input
multiple-output) systems, have become indispensable
and can be considered as an essential part of increas-
ing both the achievable capacity and integrity of fu-
ture generations of wireless systems (Zheng and Tse,
2003), (K¨uhn, 2006).
Since the capacity of MIMO systems increases
linearly with the minimum number of antennas at
both, the transmitter as well as the receiver side,
MIMO schemes have attracted substantial attention
(McKay and Collings, 2005), (Mueller-Weinfurtner,
2002).
With the increasing desire for high-data rate com-
munication, frequency non-selective MIMO links
have reached a state of maturity. By contrast, fre-
quency selective MIMO links require substantial fur-
ther research. Spatial-temporal vector coding (STVC)
introduced by RALEIGH seems to be an appropriate
candidate for broadband transmission channels. Un-
fortunately, such solutions appear to be highly com-
plex (Raleigh and Cioffi, 1998), (Raleigh and Jones,
1999). Therefore, complexity-reduced solutions are
77
Aust S., Ahrens A. and Benavente-Peces C..
MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED MULTIUSER MIMO-OFDM SYSTEMS.
DOI: 10.5220/0003443900770086
In Proceedings of the International Conference on Wireless Information Networks and Systems (WINSYS-2011), pages 77-86
ISBN: 978-989-8425-73-7
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

of great interest, where multicarrier transmission such
as OFDM combined with multiple transmit and re-
ceive antennas seems to be a promising solution to
reduce the complexity significantly.
The combination of MIMO transmission and
OFDM, as investigated in this work, can be consid-
ered as an essential part of fulfilling the requirements
of future generations of wireless systems. However
single-user scenarios have reached a state of maturity.
By contrast multiple users’ scenarios in frequency-
selective channel conditions require substantial fur-
ther research (Ahrens and Benavente-Peces, 2010),
(Liu et al., 2008).
Considering the entirety of the antennas of all mo-
bile terminals at one end and the antennas of the base
station at the other end of the communication link,
state of the art interference cancellation is based on
a central signal processing unit, e. g. a central unit
at the base station, where joint detection can be ap-
plied in the uplink (UL) and joint transmission in the
downlink (DL), respectively (Meurer et al., 2000),
(Choi and Murch, 2004), (Joham et al., 2005). Widely
used linear preprocessing techniques such as Mini-
mum Mean Square Error or Zero Forcing (ZF) have
attracted a lot of research and have reached a state of
maturity, too (Choi and Murch, 2003).
Multiple users’ scenarios in frequency-selective
MIMO channels using STVC were investigated in
(Ahrens and Benavente-Peces, 2010), where, based
on the proposed signal processing, multiuser as well
as multi-antenna interferences are perfectly elimi-
nated. Therein, it was shown that not necessarily all
user-specific MIMO layers have to be activated in or-
der to minimize the overall BER. Furthermore, power
allocation was found to be beneficial for minimizing
the overall BER.
Against this background, in this paper a SVD-
assisted multiuser MIMO-ODFM scheme is investi-
gated, where multiuser interferences as well as multi-
antenna interferences are perfectly eliminated on each
subcarrier. Instead of treating all users’ channels
jointly as in ZF (zero-forcing) multiuser transmission
techniques, the investigated solutions take the indi-
vidual users’ channel characteristics into account (Liu
et al., 2008). The novel contribution of this paper is
that we demonstrate the benefits of amalgamating a
suitable choice of activated MIMO layers and num-
ber of bits per subcarrier along with the appropriate
allocation of the transmit power under the constraint
of a given fixed data throughput.
The remaining part of this paper is organized as
follows: Section 2 introduces the subcarrier-specific
MIMO-OFDM system model, while the proposed so-
lutions of bit and power allocation are discussed in
section 3. The associated performance results are pre-
sented and interpreted in section 4. Finally, section 5
provides some concluding remarks.
2 MIMO-OFDM SYSTEM MODEL
In this section a subcarrier-specific MIMO-OFDM
system model for both single-user and multi-user
scenarios is developed where the arising subcarrier-
specific interferences are perfectly eliminated. The
system model considered in this work consists of a
single base station (BS) supporting K mobile stations
(MSs). The BS is equipped with n
T
transmit antennas,
while the kth (with k = 1,..., K) MS has n
Rk
receive
antennas, i. e. the total number of receive antennas
including all K MSs is given by n
R
=
∑
K
k=1
n
Rk
.
In order to combat the effects of the frequency se-
lective MIMO channel, OFDM is used as transmis-
sion technique (Bahai and Saltzberg, 1999), (Bing-
ham, 2000). Together with a sufficient guard in-
terval length, interferences between the subcarriers
can be avoided and only symbols that are transmit-
ted over the different antennas at same subcarrier can
interfere each other. Thus, the arising multi-antenna
and multiuser interferences between the different data
streams, transmitted over the same subcarrier, re-
quire appropriate subcarrier-specific signal process-
ing strategies.
2.1 Single-user System
Considering a single-user MIMO link (K = 1) com-
posed of n
T
transmit and n
R
receive antennas, the
obtained (n
R
,n
T
)-MIMO-OFDM system transmits an
N-point IFFT (N subchannels) modulated data signal
over every transmit antenna. The subcarrier-specific
system is modelled by
u
(κ)
= H
(κ)
·c
(κ)
+ n
(κ)
. (1)
In (1), the (n
T
×1) vector c
(κ)
contains the complex
input symbols transmitted over the κth subcarrier on
each input. Applying OFDM with a sufficient guard
interval length, the (n
R
×n
T
) matrix H
(κ)
in (1) results
in
H
(κ)
=
h
(κ)
11
··· h
(κ)
1n
T
.
.
.
.
.
.
.
.
.
h
(κ)
n
R
1
··· h
(κ)
n
R
n
T
, (2)
with the elements h
(κ)
νµ
describing the couplings of
the data symbols on the subchannel κ. The elements
can be ascertained calculating the FFT of the chan-
nel impulse response from transmitter µ to receiver
WINSYS 2011 - International Conference on Wireless Information Networks and Systems
78

Figure 1: Resulting single-user SVD-based MIMO-OFDM
system model with guard interval (GI).
ν. Finally, u
(κ)
describes the (n
R
×1) received vector
and n
(κ)
is the (n
R
×1) vector of the Additive, White
Gaussian Noise (AWGN) having a variance of U
2
R
for
both the real and imaginary parts.
The subcarrier-specific interference, introduced
by the non-diagonal matrix H
(κ)
, requires appropri-
ate signal processing strategies. A popular technique
is based on the singular-value decomposition (SVD)
of the matrix H
(κ)
, which can be written as
H
(κ)
= U
(κ)
·V
(κ)
·D
(κ)H
, (3)
where U
(κ)
and D
(κ)
H
are unitary matrices and V
(κ)
is
a real-valued diagonal matrix of the positive square
roots of the eigenvalues of the matrix H
(κ)
H
H
(κ)
sorted in descending order. The transpose and con-
jugate transpose (Hermitian) of D
(κ)
are denoted by
D
(κ)T
and D
(κ)
H
, respectively. Using D
(κ)
as prepro-
cessing matrix at the transmitter side and U
(κ)H
as
postprocessing matrix at the receiver side, the over-
all transmission relationship results in
y
(κ)
= U
(κ)H
H
(κ)
·D
(κ)
·c
(κ)
+ n
(κ)
= V
(κ)
·c
(κ)
+ w
(κ)
. (4)
Thereby, as D
(κ)
and U
(κ)H
are unitary matrices,
neither the transmit power nor the noise power is
enhanced. The resulting single-user SVD-based
MIMO-OFDM system model is represented in Fig. 1.
As a consequence of the processing in (4), the
subcarrier-specific channel matrix H
(κ)
is trans-
formed into independent, non-interfering layers hav-
ing unequal gains. The resulting subcarrier-specific
layer-based MIMO-OFDM system model is high-
lighted in Fig. 2.
c
(κ)
1,ℓ
y
(κ)
1,ℓ
w
(κ)
1,ℓ
q
ξ
(κ)
1,ℓ
Figure 2: Resulting subcarrier-specific layer-based single-
user MIMO-OFDM system model.
The data symbol c
(κ)
1,ℓ
to be transmitted over the
layer ℓ (with ℓ = 1, 2, ... ,min(n
T
,n
R
)) at the subcar-
rier κ (with κ = 1,2,.. .,N) is weighted by the layer-
specific factor
q
ξ
(κ)
1,ℓ
, corresponding to the positive
square root of the eigenvalue in V
(κ)
, and together
with the additivenoise term w
(κ)
1,ℓ
the receiveddata y
(κ)
1,ℓ
results in
y
(κ)
1,ℓ
=
q
ξ
(κ)
1,ℓ
·c
(κ)
1,ℓ
+ w
(κ)
1,ℓ
. (5)
Therein, the number of easily separable layers per
subcarrier L is limited by the minimum numbers of
antennas at both sides, the transmitter as well as the
receiver side, i. e.,
L ≤min(n
T
,n
R
) . (6)
However, it is worth noting that with the aid of
powerful non-linear near Maximum Likelihood (ML)
sphere decoders it is possible to separate n
R
> n
T
number of layers (Hanzo and Keller, 2006).
2.2 Multi-user System
Now, the subcarrier-specific single-user MIMO-
OFDM system model (K = 1) is extended by consid-
ering a single base station (BS) supporting K mobile
stations (MSs). The (n
Rk
×1) user specific symbol
vector c
(κ)
k
to be transmitted by the BS over the sub-
carrier κ is given by
c
(κ)
k
=
c
(κ)
k,1
,c
(κ)
k,2
,. .. ,c
(κ)
k,n
Rk
T
. (7)
The vector c
(κ)
k
is preprocessed before its transmis-
sion by multiplying it with the (n
T
×n
Rk
) subcarrier-
specific DL preprocessing matrix R
(κ)
k
and results in
the (n
T
×1) user-specific transmit vector
s
(κ)
k
= R
(κ)
k
c
(κ)
k
. (8)
After subcarrier-specific DL transmitter preprocess-
ing, the n
T
-component signal s
(κ)
transmitted by the
BS specific antennas over the subcarrier κ to the K
MSs results in
s
(κ)
=
K
∑
k=1
s
(κ)
k
= R
(κ)
c
(κ)
, (9)
with the (n
T
×n
R
) preprocessing matrix
R
(κ)
=
R
(κ)
1
,R
(κ)
2
,. .. ,R
(κ)
K
. (10)
In (9), the overall (n
R
×1) transmitted DL data vector
c
(κ)
combines all K DL transmit vectors c
(κ)
k
(with k =
1,2,. .., K) and is given by
c
(κ)
=
c
(κ)T
1
,c
(κ)T
2
.. ., c
(κ)T
K
T
. (11)
MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED MULTIUSER MIMO-OFDM SYSTEMS
79

At the receiver side, the (n
Rk
×1) vector u
(κ)
k
of the
kth MS is given by
u
(κ)
k
= H
(κ)
k
s
(κ)
+ n
(κ)
k
= H
(κ)
k
R
(κ)
c
(κ)
+ n
(κ)
k
. (12)
and can be expressed by
u
(κ)
k
= H
(κ)
k
R
(κ)
k
c
(κ)
k
+
K
∑
i=1,i6=k
H
(κ)
k
R
(κ)
i
c
(κ)
i
+ n
(κ)
k
,
(13)
where the MSs received signals at the subcarrier κ
(with κ = 1,2,. .., N) experience both multi-user and
multi-antenna interferences. In (12), the (n
Rk
×n
T
)
subcarrier-specific channel matrix H
(κ)
k
connects the
n
T
BS specific transmit antennas with the n
Rk
receive
antennas of the kth MS.
The subcarrier-specific interference, which is in-
troduced by the off-diagonal elements of the channel
matrix H
(κ)
k
, requires appropriate signal processing
strategies. A popular technique is based on the SVD
of the system matrix H
(κ)
k
. Upon carrying out the
SVD of H
(κ)
k
with n
T
≥n
R
and assuming that the rank
of the matrix H
(κ)
k
equals n
Rk
, i.e., rank(H
(κ)
k
) = n
Rk
,
we get
H
(κ)
k
= U
(κ)
k
·V
(κ)
k
·D
(κ)H
k
, (14)
with the (n
Rk
× n
Rk
) unitary matrix U
(κ)
k
and the
(n
T
× n
T
) unitary matrix D
(κ)H
k
, respectively. The
(n
Rk
×n
T
) diagonal matrix V
(κ)
k
can be decomposed
into a (n
Rk
×n
Rk
) matrix V
(κ)
ku
containing the non-
zero square roots of the eigenvalues of H
(κ)H
k
H
(κ)
k
,
i. e.,
V
(κ)
ku
=
q
ξ
(κ)
k,1
0 ··· 0
0
q
ξ
(κ)
k,2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ···
q
ξ
(κ)
k,n
Rk
, (15)
and a (n
Rk
×(n
T
−n
Rk
)) zero-matrix V
(κ)
kn
according
to
V
(κ)
k
=
V
(κ)
ku
V
(κ)
kn
=
V
(κ)
ku
0
. (16)
Additionally, the (n
T
×n
T
) unitary matrix D
(κ)
k
can be
decomposed into a (n
T
×n
Rk
) matrix D
(κ)
ku
constituted
by the eigenvectors corresponding to the non-zero
eigenvalues of H
(κ)H
k
H
(κ)
k
and a (n
T
×(n
T
−n
Rk
)) ma-
trix D
(κ)
kn
constituted by the eigenvectors correspond-
ing to the zero eigenvalues of H
(κ)H
k
H
(κ)
k
. The decom-
position of the matrix D
(κ)H
k
results in
D
(κ)H
k
=
D
(κ)H
ku
D
(κ)H
kn
!
. (17)
Finally, the subcarrier-specific downlink received sig-
nal u
(κ)
k
of the kth MS may be expressed as
u
(κ)
k
= U
(κ)
k
V
(κ)
ku
D
(κ)H
ku
R
(κ)
c
(κ)
+ n
(κ)
k
, (18)
with the vector n
(κ)
k
of the Additive, White Gaussian
Noise (AWGN). Taking all MSs received DL signals
u
(κ)
k
into account, the (n
R
×1) receive vector results
in
u
(κ)
=
u
(κ)T
1
,u
(κ)T
2
,. .. ,u
(κ)T
K
T
. (19)
The overall DL signal vector u
(κ)
including the re-
ceived signals of all K MSs can be expressed by
u
(κ)
= U
(κ)
V
(κ)
u
D
(κ)H
u
R
(κ)
c
(κ)
+ n
(κ)
, (20)
with the overall (n
R
×1) noise vector
n
(κ)
=
n
(κ)T
1
,n
(κ)T
2
,. .. ,n
(κ)T
K
T
, (21)
the (n
R
×n
R
) block diagonal matrix U
(κ)
U
(κ)
=
U
(κ)
1
0 ··· 0
0 U
(κ)
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· U
(κ)
K
, (22)
the (n
R
×n
R
) block diagonal matrix V
(κ)
u
V
(κ)
u
=
V
(κ)
1u
0 ··· 0
0 V
(κ)
2u
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· V
(κ)
Ku
, (23)
and the (n
T
×n
R
) matrix D
(κ)
u
which is given by
D
(κ)
u
=
D
(κ)
1u
,D
(κ)
2u
,. .. ,D
(κ)
K u
. (24)
In order to suppress the DL multiuser interferences
(MUI) at the subcarrier κ perfectly, the DL prepro-
cessing matrix R
(κ)
has to be designed to satisfy the
following condition
D
(κ)H
u
R
(κ)
= P
(κ)
, (25)
with the real-valued (n
R
×n
R
) diagonal matrix P
(κ)
taking the transmit-power constraint into account. In
order to satisfy (25), R
(κ)
can be defined as follows
R
(κ)
= D
(κ)
u
D
(κ)H
u
D
(κ)
u
−1
P
(κ)
. (26)
WINSYS 2011 - International Conference on Wireless Information Networks and Systems
80
Taking the ZF design criterion for the DL prepro-
cessing matrix into account, the matrix P
(κ)
simpli-
fies to an (n
R
× n
R
) diagonal matrix, i. e. P
(κ)
=
p
β
(κ)
I
n
R
×n
R
, with the parameter
p
β
(κ)
describing
the transmit-power constraint. When taking the DL
preprocessing matrix, defined in (26), into account,
the overall subcarrier-specific received vector of all K
MSs, defined in (20), can be simplified to
u
(κ)
= U
(κ)
V
(κ)
u
P
(κ)
c
(κ)
+ n
(κ)
. (27)
Therein, the (n
R
×n
R
) block diagonal matrix P
(κ)
is
given by
P
(κ)
=
P
(κ)
1
0 ··· 0
0 P
(κ)
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· P
(κ)
K
. (28)
In (27), the user-specific (n
Rk
×1) vector u
(κ)
k
can be
expressed as
u
(κ)
k
= U
(κ)
k
V
(κ)
ku
P
(κ)
k
c
(κ)
k
+ n
(κ)
k
, (29)
with the user-specific (n
Rk
×n
Rk
) power allocation
matrix
P
(κ)
k
=
q
p
(κ)
k,1
0 ··· 0
0
q
p
(κ)
k,2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ···
q
p
(κ)
k,n
Rk
.
(30)
As long as the transmit power is uniformly distributed
over the number of activated MIMO layers per sub-
carrier, the matrix P
(κ)
k
simplifies to
P
(κ)
k
=
q
β
(κ)
I
n
Rk
×n
Rk
. (31)
After postprocessing of the received signal vectors
u
(κ)
k
with the corresponding unitary matrix U
(κ)H
k
, the
user-specific decision variables at the subcarrier κ re-
sult with U
(κ)H
k
n
(κ)
k
= w
(κ)
k
in
y
(κ)
k
= U
(κ)H
k
u
(κ)
k
= V
(κ)
ku
P
(κ)
k
c
(κ)
k
+ w
(κ)
k
, (32)
or alternatively for the whole system with
U
(κ)H
n
(κ)
= w
(κ)
in
y
(κ)
= U
(κ)H
u
(κ)
= V
(κ)
u
P
(κ)
c
(κ)
+ w
(κ)
, (33)
where subcarrier-specific interferences between the
different antenna data streams as well as MUI im-
posed by the other users are avoided. The resulting
multiuser SVD-based MIMO-OFDM system model
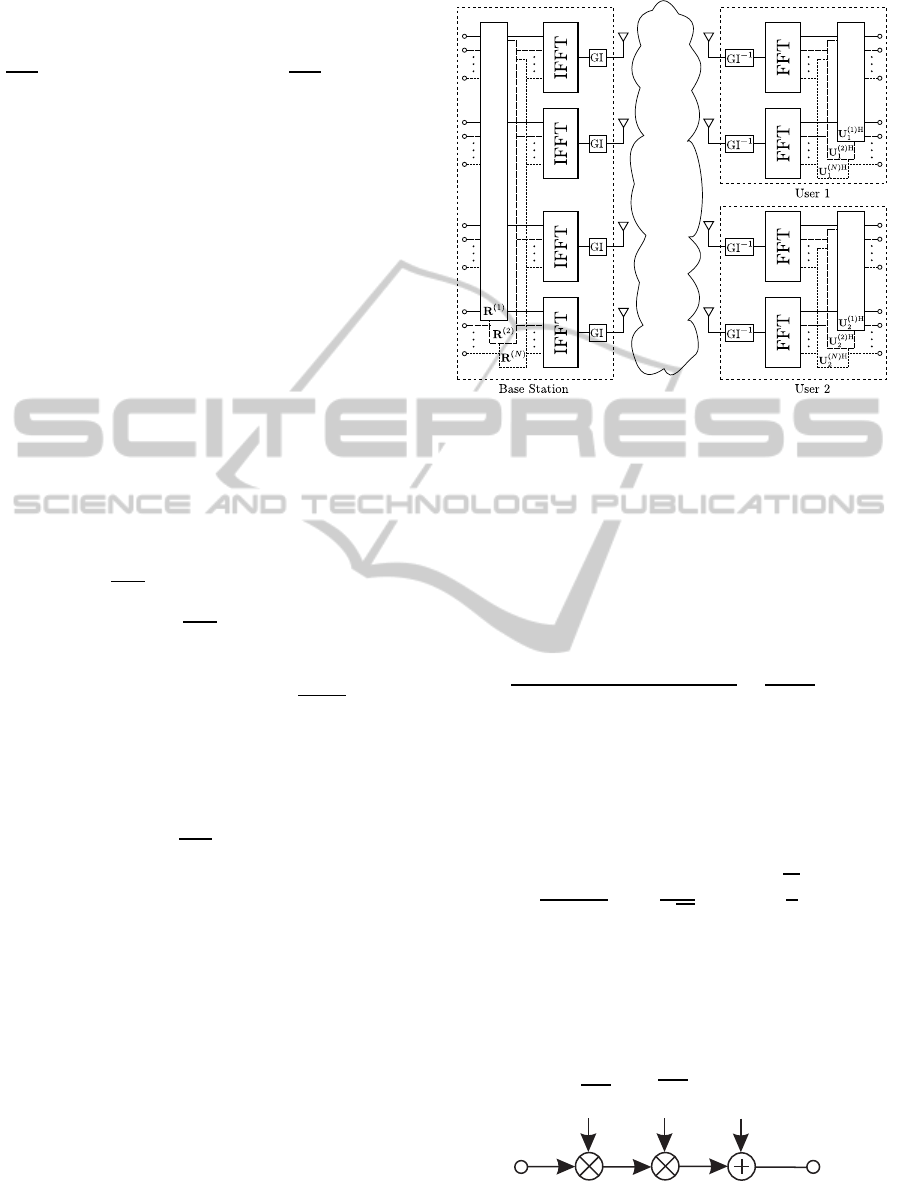
is represented in Fig. 3, whereas the resulting layer-
specific system model is depicted in Fig. 4
Figure 3: Resulting multiuser SVD-based MIMO-OFDM
system model with guard interval (GI).
3 OPTIMIZATION OBJECTIVES
In general, the user-specific quality of data transmis-
sion can be informally assessed by using the signal-
to-noise ratio (SNR) at the detector’s input defined by
the half vertical eye opening and the noise power per
quadrature component according to
ρ =
(Half vertical eye opening)
2
Noise Power
=
(U
A
)
2
(U
R
)
2
, (34)
which is often used as a quality parameter (Ahrens
and Lange, 2008). The relationship between the
signal-to-noise ratio ρ = U
2
A
/U
2
R
and the bit-error
probability evaluated for AWGN channels and M-ary
Quadrature Amplitude Modulation (QAM) is given
by (Proakis, 2000)
P
BER
=
2
log
2
(M)
1−
1
√
M
erfc
r
ρ
2
. (35)
When applying the proposed system structure for the
kth user, depicted in Fig. 4, the applied signal pro-
cessing leads to different eye openings per activated
MIMO layer ℓ (with ℓ = 1, 2,.. .,L and L ≤ n
Rk
de-
scribing the number of activated user-specific MIMO
c
(κ)
k,ℓ
y
(κ)
k,ℓ
w
(κ)
k,ℓ
q
ξ
(κ)
k,ℓ
q
p
(κ)
k,ℓ
Figure 4: Resulting kth user system model per MIMO
layer ℓ (with ℓ = 1,2,. . . ,n
Rk
) on subcarrier κ (with κ =
1,2,.. ., N).
MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED MULTIUSER MIMO-OFDM SYSTEMS
81

layers) and per subcarrier κ (with κ = 1,2,.. .,N) ac-
cording to
U
(κ)
Akℓ
=
q
p
(κ)
k,ℓ
·
q
ξ
(κ)
k,ℓ
·U
(κ)
skℓ
, (36)
where U
(κ)
skℓ
denotes the kth user and κth subcar-
rier specific half-level transmit amplitude assuming
M
ℓ
-ary QAM,
q
ξ
(κ)
k,ℓ
represents the corresponding
subcarrier-specific positive square roots of the eigen-
values of the matrix H
(κ)H
k
H
(κ)
k
and
q
p
(κ)
k,ℓ
represents
the corresponding power allocation weighting param-
eters (Fig. 4). Together with the noise power per
quadrature component, introduced by the additive,
white Gaussian noise (AWGN) vector w
(κ)
k
in (32),
the kth user-specific SNR per MIMO layer ℓ and sub-
carrier κ becomes
ρ
(κ)
kℓ
=
U
(κ)
Akℓ
2
U
2
R
. (37)
Realizing a parallel transmission over L MIMO layers
and taking all N subcarriers into account, the overall
mean user-specific transmit power becomes
P
sk
=
N
∑
κ=1
L
∑
ℓ=1
P
(κ)
skℓ
. (38)
Considering QAM constellations, the average user-
specific transmit power P
(κ)
skℓ
per MIMO layer ℓ and
subcarrier κ may be expressed as (Proakis, 2000)
P
(κ)
skℓ
=
2
3
U
(κ)
skℓ
2
(M
(κ)
kℓ
−1) . (39)
Combining (37) and (39) together with (36), the layer-
specific SNR at the subcarrier κ results in
ρ
(κ)
kℓ
= p
(κ)
k,ℓ
ξ
(κ)
k,ℓ
3
2(M
(κ)
kℓ
−1)
P
(κ)
skℓ
U
2
R
. (40)
Assuming that the user-specific transmit power is
uniformly distributed over the number of activated
MIMO layers and subcarriers, the quality on each
subcarrier is affected by both, the choice of the QAM-
constellation sizes per layer and the layer-specific
weighting factors. In order to transmit at a fixed data
rate while maintaining the best possible integrity, i. e.,
bit-error rate, an appropriate number of user-specific
MIMO layers has to be used, which depends on the
specific transmission mode, as detailed in Table 1 for
the exemplarily investigated two-user MIMO-OFDM
system (n
Rk
= 4 (with k = 1,2),K = 2,n
R
= n
T
= 8).
An optimized adaptive scheme would now use
the particular transmission modes on each subcarrier,
Table 1: Investigated user-specific transmission modes per
subcarrier.
throughput layer 1 layer 2 layer 3 layer 4
8 bit/s/Hz 256 0 0 0
8 bit/s/Hz 64 4 0 0
8 bit/s/Hz 16 16 0 0
8 bit/s/Hz 16 4 4 0
8 bit/s/Hz 4 4 4 4
e.g., by using bit auction procedures (Wong et al.,
1999), that results in the lowest BER for each MIMO-
OFDM data vector. However, this would lead to a
high signaling overhead. Therefore, in order to avoid
any signalling overhead, fixed transmission modes are
used in this contribution regardless of the channel
quality.
However, it is worth mentioning that in systems
where channel state information is available at the
transmitter side, the knowledge about how the sym-
bols are attenuated by the channelcan be used to adapt
the transmit parameters. In this context, power allo-
cation (PA) can be used to balance the bit-error prob-
abilities in the number of activated MIMO layers.
Applying PA, the information about how the sym-
bols are attenuated by the channel, i. e., the singular-
values, has to be sent via a feedback channel to the
transmitter side and leads to a signalling overhead that
is contradictory to the fix transmission modes that re-
quire no signalling overhead. However, as shown in
(Ahrens and Lange, 2009) a vector quantizer (VQ)
can be used to keep the signalling overhead moderate.
Here, a VQ for the power allocation parameters in-
stead of the singular values guarantees a better adap-
tion at a given codebook size, since the power level
vectors has less or equal dimensions than the singular-
value vectors (Ahrens and Lange, 2009). Moreover,
its elements are much smaller digits ranged from 0
to 1, rather than from 0 to +∞ in the singular-value
vector case. Hence, the entropy of the power level
vectors is smaller, which benefits the quantization ac-
curacy and the feedback overhead.
Therefore, besides the choice of the transmission
modes, PA can be used to adjust the bit-error proba-
bilities in the activated user-specific MIMO layers and
has been widely investigated in the literature (Kron-
gold et al., 2000), (Ahrens and Lange, 2008), (Jang
and Lee, 2003).
Analysing the considered MIMO-OFDM system,
the user-specific BER of the MIMO-OFDM system
is dominated by the specific layers having the low-
est SNR’s. As a remedy, a MIMO-layer transmit PA
scheme is required for minimizing the overall BER
WINSYS 2011 - International Conference on Wireless Information Networks and Systems
82
under the constraint of a limited total MIMO transmit
power.
The proposed PA scheme scales the kth user half-
level transmit amplitude U
(κ)
skℓ
of the ℓth MIMO layer
on the subcarrier κ by the factor
q
˜p
(κ)
k,ℓ
. This re-
sults in a MIMO layer-specific transmit amplitude of
U
(κ)
skℓ
q
˜p
(κ)
k,ℓ
for the QAM symbol of the transmit data
vector transmitted at the subcarrier κ over the MIMO
layer ℓ. Together with the DL preprocessing design,
the layer-specific power allocation parameter at the
subcarrier κ results in:
q
p
(κ)
k,ℓ
=
q
β
(κ)
q
˜p
(κ)
k,ℓ
. (41)
PA has been widely investigated in the literature,
where optimum solutions tends to be highly complex
(Ahrens and Lange, 2007). In this work a subopti-
mum solution is presented which focusses on the user-
specific subcarriers.
A natural choice is to opt for a PA scheme, which
results in an identical signal-to-noise ratio
ρ
(κ)
PAkℓ
=
U
(κ)
PAkℓ
2
U
2
R
= ˜p
(κ)
k,ℓ
3ξ
(κ)
k,ℓ
β
(κ)
LN (M
(κ)
kℓ
−1)
E
s
N
0
(42)
for all activated user-specific MIMO layers as shown
in (Ahrens and Lange, 2007), i.e., in
ρ
(κ)
PAkℓ
= constant (43)
for ℓ = 1,2,.. .,L and κ = 1,2,. .., N. In this particu-
lar case, nearly the same BER can be achieved on all
activated user-specific MIMO layers and subcarriers
(Ahrens and Lange, 2007).
The proposed suboptimum PA scheme focusses
on the arguments of the complementary error function
and neglects the transmission mode specific factors in
front of the complementary error function. However,
their influence, introduced by the layer-specific QAM
constellation sizes, is by far too small to generate re-
markable differences in the performance as shown in
(Ahrens and Lange, 2007).
4 RESULTS
In this contribution the efficiency of fixed user-
specific transmission modes on each subcarrier is
studied regardless of the channel quality. Assum-
ing predefined transmission modes, a fixed data rate
can be guaranteed. In order to obtain numerical re-
sults for the analyzed subcarrier-specific signal pro-
cessing strategies, a two-path channel model is in-
vestigated under time-variant conditions between any
10 15 20 25
10
−8
10
−6
10
−4
10
−2
10 ·log
10
(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0,0) QAM
(64,4,0,0) QAM
(16,16,0,0) QAM
(16,4,4,0) QAM
(4,4,4,4) QAM
Figure 5: BER without PA when using the transmission
modes introduced in Tab. 1 and transmitting 8 bit/s/Hz per
subcarrier.
given transmit and receive antenna combination. The
exemplary impulse response between the µth transmit
and νth receive antenna as a function of the multicar-
rier symbol duration T
s
is given by
g
(νµ)
k
(t,τ) = g
k,0
(t) ·δ(τ) + g
k,1
(t) ·δ(τ−3/2T
s
) ,
(44)
whereby the time-variant behaviour is described by
g
k,0
(t) and g
k,1
(t), respectively. It is assumed that the
path amplitudes have the same averaged power and
undergo a Rayleigh distribution (P¨atzold, 2002). Fur-
thermore, a block fading channel model is applied,
i. e., the channel is assumed to be time invariant for
the duration of one MIMO-OFDM data vector includ-
ing a guard interval length of T
g
= T
s
/2. The number
of subcarrier of the investigated OFDM system was
exemplarily chosen to be N = 4.
4.1 Single-user System
Considering a single-user MIMO-OFDM link (K = 1)
composed of n
T
= 4 transmit and n
R
= 4 receive an-
tennas, the corresponding calculated BER curves are
depicted in Fig. 5 for the different subcarrier-specific
QAM constellation sizes and MIMO configurations
of Table 1, when transmitting at a fixed bandwidth ef-
ficiency of 8 bit/s/Hz per subcarrier.
Assuming a uniform distribution of the transmit
power over the number of activated MIMO layers per
subcarrier, it still turns out that not all subcarrier-
specific MIMO layers have to be activated in order
to achieve the best system performance.
However, the lowest BERs can only be achieved
by using bit auction procedures leading to a high sig-
nalling overhead (Wong et al., 1999). Analyzing the
probability of choosing subcarrier-specific transmis-
sion modes by using optimal bitloading, as depicted
MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED MULTIUSER MIMO-OFDM SYSTEMS
83

in Table 2, it turns out that only an appropriate num-
ber of subcarrier-specific MIMO layers has to be ac-
tivated to reach the best results, e.g., the (16,4, 4, 0)
QAM configuration. Therefore, the results, obtained
by using bit auction procedures, justify the choice of
fixed subcarrier-specific transmission modes regard-
less of the channel quality as investigated in this con-
tribution.
Table 2: Probability of choosing subcarrier-specific trans-
mission modes at a fixed data rate by using optimal bitload-
ing (10·lg(E
s
/N
0
) = 10 dB and κ = 3).
mode (16,4,4, 0) (16,16,0,0) (64,4, 0,0) (4,4,4,4)
pdf 0.722 0.261 0.016 0.000
Further improvements can be achieved by taking
PA into account. Adaptive power allocation has been
widely investigated in the literature (Krongold et al.,
2000), (Jang and Lee, 2003), (Park and Lee, 2004),
(Ahrens and Lange, 2008) and can be used to balance
the bit-error probabilities in the different number of
activated user-specific MIMO layers. Using power al-
location, the resulting subcarrier-specific layer-based
single-user MIMO-OFDM system model is depicted
in Fig. 6.
c
(κ)
1,ℓ
y
(κ)
1,ℓ
q
p
(κ)
1,ℓ
w
(κ)
1,ℓ
q
ξ
(κ)
1,ℓ
Figure 6: Resulting subcarrier-specific layer-based single-
user MIMO-OFDM system model using Power Allocation.
A common strategy is to use the Lagrange mul-
tiplier method in order to find the optimal value of
q
p
(κ)
1,ℓ
for each MIMO layer ℓ and subcarrier κ,
which often leads to excessive-complexity optimiza-
tion problems (Ahrens and Lange, 2007). There-
fore, suboptimal power allocation strategies having a
lower complexity are of common interest (Ahrens and
Lange, 2007), (Park and Lee, 2004).
A natural choice is to opt for a PA scheme, which
results in an identical signal-to-noise ratio
ρ
(κ)
PA1ℓ
=
U
(κ)
PA1ℓ
2
U
2
R
= ˜p
(κ)
1,ℓ
3ξ
(κ)
1,ℓ
LN (M
(κ)
1ℓ
−1)
E
s
N
0
(45)
for all activated MIMO layers ℓ and subcarriers κ,
i. e., in
ρ
(κ)
PA1ℓ
= constant , (46)
for ℓ = 1,2,. .., L and κ = 1, 2, ... ,N. The power to
be allocated to each activated MIMO layer ℓ and sub-
arrier κ can be shown to be calculated by inverting
10 15 20 25
10
−8
10
−6
10
−4
10
−2
10 ·log
10
(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0,0) QAM
(16,16,0,0) QAM
(16,4,4,0) QAM
(4,4,4,4) QAM
Figure 7: BER with PA (dotted line) and without PA (solid
line) when using the transmission modes introduced in
Tab. 1 and transmitting 8 bit/s/Hz per subcarrier.
the layer-specific part ξ
(κ)
1,ℓ
/(M
(κ)
1ℓ
−1) and taking the
transmit power constraint into account as presented in
(Ahrens and Lange, 2007). In this case for each sym-
bol of the transmitted MIMO-OFDM symbol vector
the same half vertical eye opening can be guaranteed,
i. e.,
U
(κ)
PA1ℓ
= constant . (47)
for all activated MIMO layers ℓ (with ℓ = 1,2,.. .,L)
and all subcarrier κ (with κ = 1,2,. .., N). When
assuming an identical detector input noise variance
for each channel output symbol, the above-mentioned
equal quality scenario (46) is encountered. The only
difference between an optimum PA and the here con-
sidered equal quality scenario is the consideration of
the factor
1−1/
q
M
(κ)
1ℓ
(48)
in front of the complementary error function by the
optimum PA. However as shown by (Ahrens and
Lange, 2007) their influence is by far too small to gen-
erate remarkable differences in the performance.
Analyzing (46) for a given MIMO-OFDM data
block, nearly the same BER can be achieved on all ac-
tivated MIMO layers and subcarriers. However, tak-
ing the time-variant nature of the transmission chan-
nel into account, different BERs arise for different
MIMO-OFDM data blocks. Therefore, the BER of
the MIMO-OFDM system is mainly dominated by the
data blocks having the lowest SNRs. In order to over-
come this problem, the number of transmit or receive
antennas has to be increased, or coding overthe differ-
ent data blocks should be used (Ahrens et al., 2008).
As shown in Fig. 7, taking all subcarrier into ac-
count, unequal PA is only effective in conjunction
with the optimum number of MIMO layers and at
high SNR.
WINSYS 2011 - International Conference on Wireless Information Networks and Systems
84

10 15 20 25
10
−2
10
−1
10 ·log
10
(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0,0) QAM
(64,4,0,0) QAM
(16,16,0,0) QAM
(16,4,4,0) QAM
(4,4,4,4) QAM
Figure 8: SVD-based user-specific BERs without PA when
using the transmission modes introduced in Table 1 and
transmitting 8 bit/s/Hz per subcarrier.
4.2 Multi-user System
The parameters of the analyzed two-users MIMO sys-
tem are chosen as follows: P
sk
= 1V
2
, n
Rk
= 4 (with
k = 1,2), K = 2,n
R
= n
T
= 8. In this contribution a
power with the dimension (voltage)
2
(in V
2
) is used.
At a real constant resistor this value is proportional to
the physical power (in W).
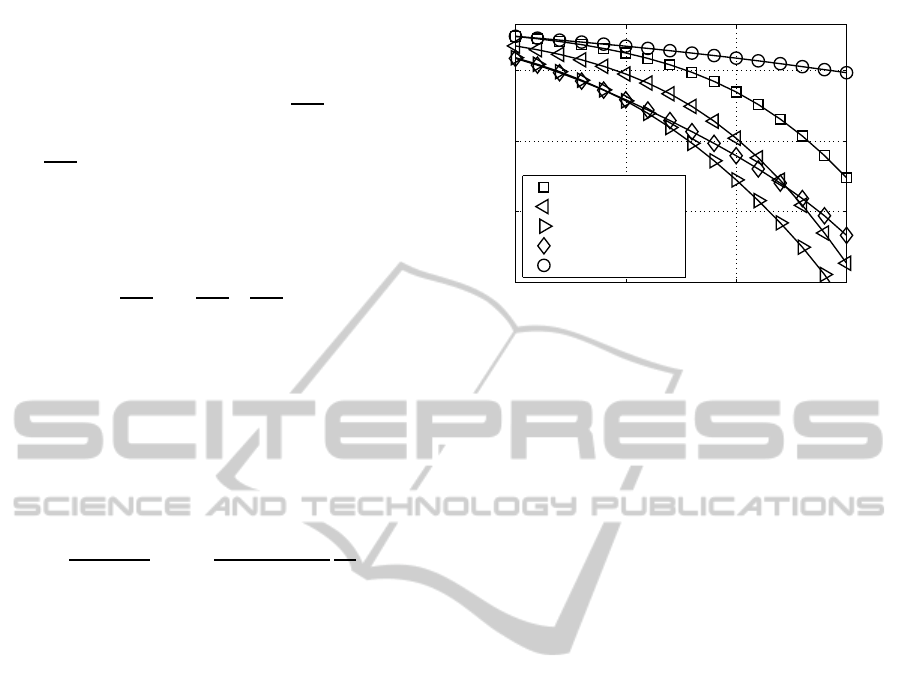
The obtained user-specific BER curves are de-
picted in Fig. 8 for the different subcarrier-specific
QAM constellation sizes and MIMO configurations
of Table 1 and confirm the obtained results within the
single-user MIMO-OFDM system (K = 1). Based on
the higher total subcarrier-specific throughput within
the given bandwidth compared to the single-user
system, the gap between the different transmission
modes becomes smaller.
Assuming a uniform distribution of the transmit
power over the number of activated MIMO layers,
it still turns out that not all MIMO layers per sub-
carrier have to be activated in order to achieve the
best BERs. This can still be confirmed by analyzing
the probability of choosing user-specific transmission
modes within the multiuser DL MIMO-OFDM sys-
tem by using optimal bitloading (Wong et al., 1999),
as depicted in Table 3.
The partitioning of the transmit power to the sub-
Table 3: Probability of choosing user-specific transmission
modes (K = 2) per subcarrier at a fixed data rate by using
optimal bitloading (10·log
10
(E
s
/N
0
) = 10 dB and κ = 3).
mode (16,4,4, 0) (16,16,0,0) (64,4, 0,0) (4,4,4,4)
pdf 0.950 0.010 0.000 0.039
10 15 20 25
10
−2
10
−1
10 ·log
10
(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0,0) QAM
(16,4,4,0) QAM
(4,4,4,4) QAM
Figure 9: SVD-based user-specific BERs with PA (dotted
line) and without PA (solid line) when using the transmis-
sion modes introduced in Table 1 and transmitting 8 bit/s/Hz
per subcarrier.
channels is a degree of freedom in the multiuser sys-
tem too and has to be done in such a manner, that
for the whole system a maximum performance with
respect to a given quality criterion and given bound-
ary conditions can be achieved (e. g. minimum bit-
error rate with limited transmit power). In the pro-
posed multiuser MIMO-OFDM system, user-specific
PA can be done, i. e., the available transmit power per
user P
sk
= 1V
2
can be distributed over all activated
user-specific layers on all subcarrier. The obtained
BER curves are depicted in Fig. 9.
As developed within the single-user MIMO-
OFDM system, unequal PA based on the proposed
equal-quality scenario is only effective in conjunc-
tion with the optimum number of MIMO layers and at
high SNR. At the low SNR, as depicted in Fig. 9, the
proposed equal-quality scenario doesn’t lead to any
improvement. Here our results suggest that a uniform
distribution of the transmit power seems to be a good
choice for minimizing the overall BER.
5 CONCLUSIONS
In this paper, the DL performance of a multiuser
MIMO-OFDM system is investigated theoretically
and by software simulation. Frequency selective
MIMO channels are considered and conditions to
eliminate multiuser and multi-antenna interferences
on each subcarrier are established using the SVD of
the individual user subcarrier-specific channel matrix.
Furthermore, bit and power allocation in multiuser
MIMO-OFDM systems were investigated for con-
stant data throughput per subcarrier. Here, it turned
out that the choice of the number of bits per symbol
MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED MULTIUSER MIMO-OFDM SYSTEMS
85

as well as the number of activated MIMO layers per
subcarrier substantially affects the performance of a
MIMO-OFDM system, suggesting that not all user-
specific MIMO layers per subcarrier have to be acti-
vated in order to achieve the best BERs. Addition-
ally, unequal PA was found to be effective in conjunc-
tion with the optimum number of MIMO layers for
the overall performance at the high SNR.
REFERENCES
Ahrens, A. and Benavente-Peces, C. (2010). Modulation-
Mode and Power Assignment for SVD-assisted and
Iteratively Detected Downlink Multiuser MIMO Sys-
tems. In International Conference on Wireless Infor-
mation Networks and Systems (WINSYS), pages 107–
114, Athens (Greece).
Ahrens, A., K¨uhn, V., and Weber, T. (2008). Iterative De-
tection for Spatial Multiplexing with Adaptive Power
Allocation. In 7th International Conference on Source
and Channel Coding (SCC), Ulm.
Ahrens, A. and Lange, C. (2007). Transmit Power Alloca-
tion in SVD Equalized Multicarrier Systems. Inter-
national Journal of Electronics and Communications
(AE
¨
U), 61(1):51–61.
Ahrens, A. and Lange, C. (2008). Modulation-Mode and
Power Assignment in SVD-equalized MIMO Sys-
tems. Facta Universitatis (Series Electronics and En-
ergetics), 21(2):167–181.
Ahrens, A. and Lange, C. (2009). Modulation-Mode and
Power Assignment in SVD-assisted MIMO Systems
with limited Feedback. In First Asian Conference on
e-Business and Telecommunications (CeBT), pages 1–
18, Changhua City (Taiwan).
Bahai, A. R. S. and Saltzberg, B. R. (1999). Multi-Carrier
Digital Communications – Theory and Applications of
OFDM. Kluwer Academic/Plenum Publishers, New
York, Boston, Dordrecht, London, Moskau.
Bingham, J. A. C. (2000). ADSL, VDSL, and Multicarrier
Modulation. Wiley, New York.
Choi, R. L. and Murch, R. D. (2003). New Transmit
Schemes and Simplified Receivers for MIMO Wire-
less Communication Systems. IEEE Transactions on
Wireless Communications, 2(6):1217–1230.
Choi, R. L. and Murch, R. D. (2004). A Transmit Prepro-
cessing Technique for Multiuser MIMO Systems us-
ing a Decomposition Approach. IEEE Transactions
on Wireless Communications, 3(1):20–24.
Hanzo, L. and Keller, T. (2006). OFDM and MC-CDMA.
Wiley, New York.
Hwang, T. J., Hwang, H. S., and Balik, H. K. (2003). Adap-
tive OFDM with Channel Predictor over Frequency-
Selective and Rapid Fading Channel. In Personal,
Indoor and Mobile Radio Communications (PIMRC),
pages 859–863, Bejing (China).
Jang, J. and Lee, K. B. (2003). Transmit Power Adapta-
tion for Multiuser OFDM Systems. IEEE Journal on
Selected Areas in Communications, 21(2):171–178.
Joham, M., Utschick, W., and Nossek, J. A. (2005). Lin-
ear Transmit Processing in MIMO Communications
Systems. IEEE Transactions on Signal Processing,
53(8):2700–2712.
Krongold, B. S., Ramchandran, K., and Jones, D. L.
(2000). Computationally Efficient Optimal Power Al-
location Algorithms for Multicarrier Communications
Systems. IEEE Transactions on Communications,
48(1):23–27.
K¨uhn, V. (2006). Wireless Communications over MIMO
Channels – Applications to CDMA and Multiple An-
tenna Systems. Wiley, Chichester.
Liu, W., Yang, L. L., and Hanzo, L. (2008). SVD Assisted
Joint Transmitter and Receiver Design for the Down-
link of MIMO Systems. In IEEE 68th Vehicular Tech-
nology Conference (VTC), pages 1–5, Calgary.
McKay, M. R. and Collings, I. B. (2005). Capacity
and Performance of MIMO-BICM with Zero-Forcing
Receivers. IEEE Transactions on Communications,
53(1):74– 83.
Meurer, M., Baier, P. W., Weber, T., Lu, Y., and Papathanas-
siou, A. (2000). Joint Transmission: An Advanta-
geous Downlink Concept for CDMA Mobile Radio
Systems using Time Division Duplexing. Electronics
Letters, 36(10):900–901.
Mueller-Weinfurtner, S. H. (2002). Coding Approaches for
Multiple Antenna Transmission in Fast Fading and
OFDM. IEEE Transactions on Signal Processing,
50(10):2442–2450.
Park, C. S. and Lee, K. B. (2004). Transmit Power Alloca-
tion for BER Performance Improvement in Multicar-
rier Systems. IEEE Transactions on Communications,
52(10):1658–1663.
P¨atzold, M. (2002). Mobile Fading Channels. Wiley, Chich-
ester.
Proakis, J. G. (2000). Digital Communications. McGraw-
Hill, Boston.
Raleigh, G. G. and Cioffi, J. M. (1998). Spatio-Temporal
Coding for Wireless Communication. IEEE Transac-
tions on Communications, 46(3):357–366.
Raleigh, G. G. and Jones, V. K. (1999). Multivariate
Modulation and Coding for Wireless Communication.
IEEE Journal on Selected Areas in Communications,
17(5):851–866.
van Nee, R. and Prasad, R. (2000). OFDM for Wireless
Multimedia Communications. Artech House, Boston
and London.
Wong, C. Y., Cheng, R. S., Letaief, K. B., and Murch, R. D.
(1999). Multiuser OFDM with Adaptive Subcarrier,
Bit, and Power Allocation. IEEE Journal on Selected
Areas in Communications, 17(10):1747–1758.
Zheng, L. and Tse, D. N. T. (2003). Diversity and
Multiplexing: A Fundamental Tradeoff in Multiple-
Antenna Channels. IEEE Transactions on Information
Theory, 49(5):1073–1096.
WINSYS 2011 - International Conference on Wireless Information Networks and Systems
86
