IDENTIFICATION AND CONTROL OF AN ELECTRO

HYDRAULIC ROBOT PARTICLE SWARM

OPTIMIZATION-NEURAL NETWORK(PSO-NN) APPROACH

M. Taylan Daş

Roketsan Missile Company, Elmadağ-Ankara, Turkey

L. Canan Dülger, Sadettin Kapucu

University of Gaziantep, Department of Mechanical Engineering, Gaziantep, Turkey

Keywords: Particle Swarm Optimization, Electro-Hydraulic Robot, Neural Networks (NNs), System Identification (SI).

Abstract: This paper proposes a novel approach based on the training of the Neural Network method with Particle

Swarm Optimization (PSO-NN) for identification of a hydraulic servo robot. The robot is considered to

have two degrees of freedom; one is rotational and the other is translational. A feed forward NN is designed

for the problem and the weights of the network are trained using Particle Swarm Optimization (PSO)

algorithm. In order to demonstrate the performance of PSO-NN, the designed network is also trained and

tested with the Back Propagation (BP-NN) algorithm. Test results validated that the performance of PSO-

NN is better than BP-NN algorithm both in convergence speed and in convergence accuracy. The results

also illustrate that PSO-NN algorithm is an applicable and effective method for identification and control of

a robotic system.

1 INTRODUCTION

Neural network (NN) is a powerful tool for complex

applications including robotics and industry process,

and optimization. NNs can be used to approximate

any linear or nonlinear function. The NN controllers

hold out the potential for control systems that mimic

the human capacity for learning and how to provide

the correct input signals that result in a desired

response without detailed knowledge of the system

dynamics. A trained neural network can be thought

of as an "expert" in the category of information it

has been given to analyze. This new situation gives

an opportunity to obtain new projections of system

response (Hong et al., 2002), (Van Den Bergh,

Engelbrecht, 2000).

NNs are extensively used in the literature for

different robotic applications. Generally, NN

learning and tests are applied to forward or inverse

kinematics simulation results. (Lewis, 1996) has

introduced a NN controller design algorithms for

rigid robot arms, force control and parallel-link

robot arms. (He and Sepehri, 1999) have presented a

model and predicted the performance of hydraulic

servo actuators with experimental data. Levenberg-

Marquardt (LM) algorithm was applied to train the

network. (Abdelhameed, 1999) has developed an

adaptive NN controller for robot trajectory tracking

problem. The results for a polar robot manipulator

were presented to demonstrate the effectiveness of

proposed system. (Hong et al., 2002) have used a

multi-layer NN based on LM training algorithm for

the tracking control problem of the electro-hydraulic

servo system. (Ghobakhloo and Eghtesad, 2005)

have developed a multi-layer BP-NN algorithm to

solve the forward kinematics problem of a redundant

hydraulic shoulder having three degrees of rotational

freedom.

PSO is a population based stochastic

optimization technique developed by Dr. Eberhart

and Dr. Kennedy in 1995, inspired by social

behaviour of bird flocking or fish schooling

(Kennedy and Eberhart, 1995). Up to date, PSO

applied to many different problems. (Zhang et al.,

2000) have studied on new evolutionary system for

evolving artificial neural networks, which is based

on the PSO. The results of PSO-NN harmonize the

Taylan Da¸s M., Canan Dülger L. and Kapucu S..

IDENTIFICATION AND CONTROL OF AN ELECTRO HYDRAULIC ROBOT PARTICLE SWARM OPTIMIZATION-NEURAL NETWORK(PSO-NN)

APPROACH.

DOI: 10.5220/0003447600490055

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 49-55

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

architecture and weights of NN. (Liu et al., 2004)

have studied a different variable neighbourhood

model ‘vbest’ in PSO search method for NN

learning, instead of ‘gbest’ and ‘lbest’. (Zhang et al.,

2006) have developed a hybrid PSO-BP algorithm

for feed forward NN training. Recently, (Das and

Dulger, 2007) have recently designed a PSO

algorithm for optimizing the parameters of the PD

controller which is applied on position control of a

four bar mechanism system. Many researchers were

used NNs and their variants with PSO for different

dynamic systems.

Several studies have also been reported on

identification of hydraulic servo systems also

identification and control of dynamic systems using

NNs. It is not possible to include all applications

which NNs have been applied A few research study

is included where our study is based on them.

(Narendra and Parthasamathy, 1990) have used the

NNs for the identification and control of nonlinear

dynamic systems. (Kapucu, 1994) has performed a

study on identification of a hydraulic robot, named

as ARTISAN which will originate the study

presented here. He has taken a SISO model with

assumption of the independent joint dynamics.

Following that, MIMO model is studied to trace a

circle using finite difference equations. However,

PSO-NN algorithm is not seen any theoretical and

experimental application of a hydraulic robot system

in a literature study.

This study addresses the identification of the

hydraulic robot with PSO-NN where PSO has been

used to train the NNs. A feed forward NN based

PSO algorithm is proposed for identification a

hydraulic robot. NNs approximate arbitrary input-

output mappings to identify the unknown function.

Identification of the hydraulic robot is given in

Section 2. A brief overview on the PSO algorithm

and the application of the algorithm for the robot

identification are presented in Section 3. The

experimental system is explained in Section 4. Test

results and their validation are then presented in

Section 5. Finally conclusions are included with

comparisons on methods, PSO-NN and BP-NN

algorithm.

2 IDENTIFICATION OF

ELECTRO HYDRAULIC

ROBOT

Determining the nonlinear motion equations of

hydraulic robot is a complex process. In system

identification, mathematical models are built from

the systems experimental data. This model can be

expressed mathematically relation with the outputs

to the inputs. In this study, the problem becomes

identification of a nonlinear system to get better

control on the trajectory requirement. Initially a NN

model for the plant is developed for the system

identification. This NN plant model is then used

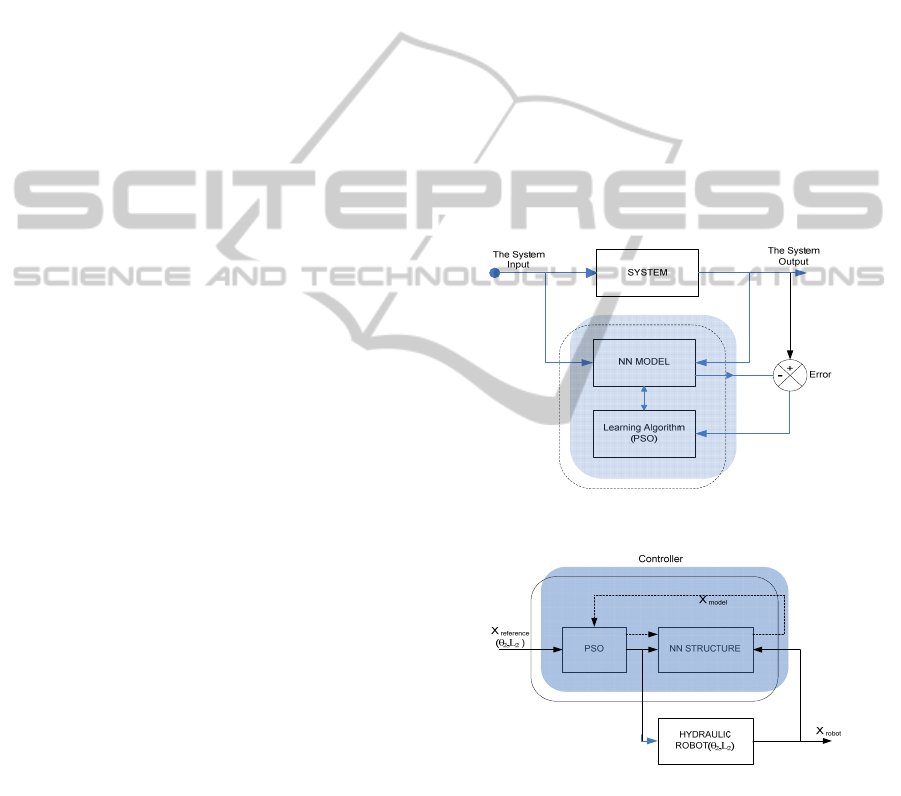
with PSO algorithm to train the controller. Referring

to (Narendra and Parthasamathy, 1990), Figure 1 can

be presented for the structure of system

identification. So the system error between the

system output and the NN output, is used the NN

training signal.

The following block diagram, Figure 2 illustrates

the control process for the robot. The NN model and

the PSO block are included in the controller. This

process can be performed for each axis of the

hydraulic robot, θ

and L

respectively in RP

configuration.

Figure 1: System Identification

Figure 2: The Control Block Diagram of the electro

hydraulic robot with PSO-NN.

3 CONTROL ALGORITHMS

3.1 Particle Swarm Optimization

The PSO algorithm includes a swarm of particles

moving in the n-dimensional problem space where

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

each particle is evaluated by a fitness function to be

optimized. Each particle in the swarm has a position

and a velocity. The particles fly through the problem

space by following the current optimum particles

(Kennedy and Eberhart, 1995). PSO is initialized

with a group of random particles (solutions) and

then searches for the optimum by updating

generations. Each particle is updated by following

two "best" values. The first one is the best solution

best

that a particle has achieved so far. The other one

is the global best value g

best

that is obtained by any

particle in the population so far. After finding the

two best values, the particle updates its velocity and

positions with following equations.

)()(

2211

ibest

best

xgrcxprcwvv −+−+=

(1)

11 ++

vxx

(2)

is the particle velocity, x

is the current

particle (solution), p

best

is the best solution value

among the particle found in the current iteration, g

best

is the global best solution achieved so far, r

, r

are

random numbers between (0, 1), c

are the

learning factors usually taken as c

=2.

The performance of the PSO algorithm depends

on many parameters; the number of particles and the

maximum velocity parameter. This parameter affects

the run-time significantly; a balance between more

particles (variety) and fewer particles (speed) should

be evaluated in the swarm. The maximum velocity

parameter effects the convergence speed of the

algorithm limits the maximum jump that a particle

can make in one step. Thus a too large value for this

parameter will result in oscillations, while a too

small value could cause the particle to become

trapped in local minima (Bose and Liang, 1996).

3.2 Back Propagation NNs

Both Multi-layer and single perceptions are mostly

trained with BP algorithm in supervised learning. BP

is one of the most common neural network

structures, as it is easy to implement and efficiency

is good. Therefore BP is selected to compare with

the proposed algorithm. BP algorithm uses gradient

descent method to minimize the total squared error

of output. A BP net is a multilayer, feed forward

network that is trained by back propagating errors

using generalized delta rule (Krose and Van der

Smart, 1996). The whole back-propagation process

is very clear. When a learning pattern is clamped,

the activation values are propagated to the output

units, and the actual network output is compared

with the desired output values. It usually ends up

with an error where requirement is to bring zero in

each one of the output units.

3.3 The Proposed Algorithm

For the solution of the problem a NN structure that

the input layer N has two nodes (N=2), hidden layer

J with twenty nodes (J=20) and output layer L with

two nodes (L=2) are used. The structure of the

network can be seen in Figure 3. Pseudo-code of the

proposed algorithm is given in Table 1.

The proposed NN structure is trained with PSO

which offers a simple and effective way as a search

algorithm. Both, the hidden and the output transfer

functions are both assumed as sigmoid function. The

output of the hidden node is calculated as;

5,..,2,1))),(exp(1/(1 f(j)

=−⋅−+=

∑

jxw

nnj

θλ

(3)

Input Layer Hidden Layer Output Layer

Figure 3: General Neural Network structure of PSO-NN

algorithm.

Where w

n j

is the weights between the n

node of

input layer and j

node of hidden layer, θ

is the

threshold of the hidden layer, x

is the n

input and λ

is the activation gain. The desired output d of the l

output layer d

is;

2,1,)( =−⋅=

∑

ljfwd

lljl

(4)

Where w

is the weight from the j

hidden node

to the l

output node, θ

is the threshold of the output

layer. The error E[n] is the sum of squares of the

error over all output units; n is the set of trained

example.

)]()([

)(

∑

−=

desiredactual

ndndnE

(5)

where,

∑

nEE

)(

actual

is the actual output value taken from the

system, d

desired

is the desired output value in each

PSO

IDENTIFICATION AND CONTROL OF AN ELECTRO HYDRAULIC ROBOT PARTICLE SWARM

OPTIMIZATION-NEURAL NETWORK(PSO-NN) APPROACH

iteration and E

is the total error. This error is

accepted as the fitness function of a particle that can

be calculated by

)(

∑

−

desiredactual

EparticleFitness

(6)

The weights between the n

node of input layer

and j

node of hidden layer (w

, w

,…,w

, w

) and

the j

node of hidden and l

node of the output layer

, w

,…,w

, w

) are represented as a vector.

The obtained weight vector is accepted as the

dimensions of a particle. The particle is defined as:

particle

= (w

14,

)

Table 1: The proposed PSO-NN algorithm.

Step 1: Initialization of the network

Choose the number of nodes for the

input, output and hidden layers

Step 2: Determine the Initial value of

weights between -1.0 and 1.0

Choose a learning rate between 0

and 1.0

Step3: Learning step and calculation

of the weight values.

Define PSO parameters (c

, c

,w, r

, r

)

Initialize Population

Calculate fitness value of Each

particle

While (error criteria is not attained)

{Calculate p

best

value

Calculate g

best

value

Update velocity and position

Vector of each particle Evaluate}

End Criteria (maximum iterations)

Step4: Test the accuracy of the

network on a test database.

Step5: If the accuracy is less than

the desired error rate, then

give new parameters to the

network and start again.

4 THE EXPERIMENTAL SYSTEM

The PSO-NN algorithm is applied on the spherical

hydraulically driven robot which is available at

Department of Mechanical Engineering, Dynamic

Systems Laboratory, Gaziantep University, and is

called as ‘ARTISAN’. In the literature, different

studies have been performed for the control of the

ARTISAN electro-hydraulic robot. Firstly, (Kapucu,

1994) performed a study on adaptive control of this

robot by visual data. Later, (Kirecci et al., 2003)

applied self tuning method for controlling this robot

for better trajectory tracking and presented

experimental results.

Figure 4 shows a photograph of the manipulator

which originally has 3 degrees of freedom. Two

revolute and one prismatic joint are included to

represent RRP (Revolute-Revolute-Prismatic)

configuration (Kapucu, 1994).

Figure 4: The Electro-Hydraulic Robot. (ARTISAN).

During the tests on the application of the

algorithm, its rotational joint moving perpendicular

to the horizontal plane is fixed and other joints

representing RP (Revolute-Prismatic) configuration

are controlled by servo valves in closed loop

operating in vertical plane. The experimental system

consists of a hydraulically driven spherical

manipulator, PC, an interface card for required

communication, hydraulic actuators and servo

amplifier with position transducers fitted each joint.

Block diagram for the hydraulic system is given

in Figure 5 with negative feedback. The manipulator

links are controlled by Bosch regulator valves of

0811404-028 type in a closed loop with rotary

potentiometer to obtain desired motion for each

joint. The supply of hydraulic pressure and flow to

the servo valves are provided by 22 kW hydraulic

power units which can supply up to 95 lt/min at 0.12

MPa.

Figure 5: The block diagram of system.

Three dimensional representation of the robot is

given in Figure 6. The robot end-point positions are

specified in terms of the chosen coordinates as: the

base rotation θ

, the elevation angle θ

the reach L

Forward kinematics is applied to as P

, P

and P

calculate end point positions by using configuration

of ARTISAN given Figure 6.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

022

sin

sincos

coscos

θθ

(7)

Figure 6: Configuration of ARTISAN Robot.

4.1 Test Results and Validation

Test results of the proposed PSO-NN algorithm are

presented in this section. The input values of the

joints (θ

, L

) are applied to the network as the input

1 and the input 2. Similarly, the responses of joints

are accepted as output1 and output 2. Different test

trajectories are employed to show validation of

results. In order to normalize the experimental data

to the range [0, 1], the value y(x) at each (x) point

was normalized to according to the equation given

for all input and output points.

minmax

min

)(

−

(8)

Where; y(x) is the normalized value (between 0

and 1), y is the reference value, y

min

is the minimum

allowed value {taken as (-18 degrees for the output1,

), (69cm for the output2, L

)}, y

max

is the

maximum allowed value {taken as (18 degrees for

the output1), (154cm for the output2)}

Two examples are implemented and presented

for the validation stage here. A population of 45

particles is used for the PSO-NN algorithm.

Numbers of particles and hidden layers have been

tried on the system in different in various training.

Learning factors c

and c

are set to 2.0. Both the

PSO-NN and BP-NN algorithm is trained for 5000

iterations. Learning rate and momentum rate is

chosen between 0 and 1. The initial weight values

have importance on training results if a priori

knowledge is available for weights. Initial weights

of the both algorithms are chosen between -1 and 1

randomly. Both algorithms are started with the same

initial weight values. The performance of the

proposed algorithm is tried with many different

initial weights. However, the convergence rate of the

algorithm did not change. The algorithms are coded

in C and run on a P4 with 2.4 GHz. After training

the network with the training values, the chosen test

values are fed into the trained algorithms. The

performances of PSO-NN algorithm and BP-NN

algorithm are compared with respect to the mean

squared error.

In the first example, 120 data have been recorded

experimentally in total. It represents an arbitrary

trajectory chosen for identification purpose. Half of

these data have been used for training and the rest of

the data have been used in the test session. The

position curves for the electro-hydraulic robot on the

rotational coordinate, θ

and the translational

coordinate, L

with the given signal and the output

values obtained for the test values by PSO-NN and

BP-NN algorithm are given in Figures 7(a) and 7(b).

One axis, the rotational is shown by radians and the

other axis is shown by meters, in 2 degrees of

freedom configuration (RP).

In the second example, 240 data have been

recorded experimentally. A circular trajectory is

traced in the second test by giving the coordinates of

a circle to a hydraulic robot, again representing RP

configuration. Similar to the above example, half of

these data have been used for the training and the

rest of the data have been used in the test session

Test values for circular trajectory are given in

Figures 8(a) and 8(b). In both results, Figures 7 and

8 show the reference signal with the tested

controller. The system follows the reference signal

with some error at some points. It can be seen that

PSO-NN algorithm produces better output values

than BP-NN algorithm in both examples. This error

can obviously be reduced by using more training

data, yielding increase in computation in the

network

The overall correction rate of the test results of

PSO-NN and BP-NN algorithms can be seen in

Table 2. Average rates are represented in Table 2,

additionally; PSO-NN gives better results in most

cases. The proposed PSO-NN algorithm converges

faster than BP-NN algorithm during the tests on the

electro-hydraulic system according to the reference.

Table 2 can be explained as the following. The value

of total error rate is found as 0.010995 for PSO-NN;

however total error rate of BP-NN algorithm is

0.042751 at the end of the 5000 iteration. In an

overall view, PSO-NN passed the total value of BP-

IDENTIFICATION AND CONTROL OF AN ELECTRO HYDRAULIC ROBOT PARTICLE SWARM

OPTIMIZATION-NEURAL NETWORK(PSO-NN) APPROACH

NN after the 388

iteration in the example with any

more computation. The convergence rate of both

algorithms can be seen in Figure 9.

Table 2: PSO-NN and BP-NN test results.

The 1

Test

PSO-NN

Correction Rate

(CR) (%)

BP-NN CR (%)

Output 1(θ

) 96.425 93.0746

Output 2(L

) 90.2669 88.1498

The 2

Test PSO-NN CR (%) BP-NN CR (%)

Output 1(θ

) 96,407 89.321

Output 2(L

) 95,574 86,4

5 CONCLUSIONS

In this paper, PSO-NN algorithm is proposed for the

tracking problem of the electro-hydraulic servo

robot with highly nonlinear characteristics. The

PSO-NN algorithm is compared with BP-NN

algorithm for solving the problem of identification.

For the solution of the problem, a NN structure

having the input layer N with two nodes (N=2),

hidden layer J with twenty nodes (J=20) and output

layer L with two nodes (L=2) is used. The designed

network is also trained and tested with the BP-NN

algorithm. Test results showed that the performance

of PSO-NN is better than the BP-NN algorithm in

convergence speed and in convergence accuracy.

The quality of the results illustrate that PSO-NN

algorithm is applicable and effective for the

identification of the hydraulic servo robot. The

control error for both examples converges fast. The

results can be improved by increasing the number of

data points used as the inputs and the outputs during

training. In the application of the optimization

method, it has also seen that, increasing the number

of swarms increase the number of error function

evaluations. PSO-NN gets less computation time and

higher training and test accuracies than BP-NN

algorithm.

Figure 7(a): The Translational axis (L

-0,2

0,2

0,4

0,6

0,8

1,2

0204060

Number Of Inputs

Joint1 Response(ra

Reference

PSO - NN

Figure 7(b): The Rotational axis (θ

0,2

0,4

0,6

0,8

1,2

0 20406080100120

Number of inputs

Joi nt2 Response (m)

Reference

PSO-NN

Figure 8(a): The Translational Axis (L

0,2

0,4

0,6

0,8

1,2

0 20406080100120

Number of inputs

Joi nt1 response (rad)

Reference

PSO-NN

Figure 8(b): The Rotational Axis (θ

0,2

0,4

0,6

0,8

1,2

1,4

0 1000 2000 3000 4000 5000 6000

Number of iteration

Total error rate

BP error rate

PSO-NN error rate

Figure 9: Convergence rates of proposed Algorithms.

REFERENCES

Hong Z., Kaifang D., Tingqi L., 2002. “A Online-Trained

Neural Network Controller for Electro-hydraulic

Servo System”, Proceedings of the 4

World Congress

on Intelligent Control and Automation. Shanghai,

China, pp. 2983-2986.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

Van Den Bergh F., Engelbrecht A. P., 2000. “Cooperative

Learning in Neural Networks using Particle Swarm

Optimizers”. SACJ/SART, no 26, pp. 1-8.

Lewis F. L., 1996. “Neural Network Control of Robot

Manipulators”. IEEE Expert Special track on

“Intelligent Control”, ed. K.Passino and U. Ozguner,

pp. 64-75.

He S., Sepehri N., 1999. “Modeling and Prediction of

Hydraulic Servo Actuators with Neural Networks”.

Proceedings of the American Control Conference, San

Diego, California. pp. 3708-3712.

Abdelhameed M. M., 1999. “Adaptive Neural Network

Based Controller for Robots”. Mechatronics, vol.9, pp.

147-162.

Ghobakhloo A., Eghtesad M., 2005. “Neural Network

Solution for The Forward Kinematics Problem of A

Redundant Hydraulic Shoulder”. 32

Annual

Conference of IEEE Industrial Electronics Society,

IECON2005, pp. 1999-2004.

Kennedy J., Eberhart R. C., 1995. “Particle Swarm

Optimization”. Proceedings of IEEE International

Conference on Neural Networks, Piscataway, NJ, pp.

39-43.

Zhang C., Shao H., Li Y., 2000. Particle Swarm

Optimisation for Evolving Artificial Neural Network”,

Proceedings of the IEEE International Conference on

Systems, Man. and Cybernetics 2000, pp. 2487-2490.

Liu H., Tang Y., Meng J., Ji Y., 2004. “Neural Networks

Learning Using Vbest Model Particle Swarm

Optimisation”, Proceedings of the 3

International

Conference on Machine Learning and Cybernetics,

Shanghai, China. pp. 3157-3159.

Zhang J. R., Zhang J., Lok T-M., Lyu M. R., 2006. “A

Hybrid Particle Swarm Optimization-Back

Propagation Algorithm for Feedforward neural

Network Training”. Applied Mathematics and

Computation.

Das M. T., Dulger L. C., 2007. “Control of a Four Bar

Mechanism by applying particle swarm optimization”.

National Machine Theory Symposium,

UMTS2007, Sivas, Türkiye.

Narendra K. S., Parthasamathy K., 1990. ‘Identification

and Control of Dynamical Systems Using Neural

Networks’, IEEE Transactions on Neural Networks,

Vol.1, No.1, pp. 4-27.

Kapucu S., 1994. “Adaptive Control of a Robot

Manipulator by visual data”. A Ph.D. Thesis,

Gaziantep University, Mechanical Engineering

Department.

Bose N. K., Liang P., 1996. “Neural Network

Fundamentals with Graphs, Algorithms, and

Applications”. McGraw-Hill series in electrical and

computer engineering. ISBN 0-07-114064-6.

Krose B., Van der Smart P., 1996. “An Introduction to

Neural Network”, 8

edition.

Kirecci A., Eker İ., Dülger L. C., 2003. “Self Tuning

Control as Conventional Method”, Electrical

Engineering, 85, pp. 101-107.

Bosch Regulator Valves, 1987. Robert Bosch GmbH,

Germany, 761302-1987.

IDENTIFICATION AND CONTROL OF AN ELECTRO HYDRAULIC ROBOT PARTICLE SWARM

OPTIMIZATION-NEURAL NETWORK(PSO-NN) APPROACH