COLLECTIVE CLASSIFICATION FOR UNKNOWN MALWARE

DETECTION

Igor Santos, Carlos Laorden and Pablo G. Bringas

Lab, DeustoTech - Computing Deusto Institute of Technology, University of Deusto

Avenida de las Universidades 24, 48007, Bilbao, Spain

Keywords:

Security, Computer viruses, Data-mining, Malware detection, Machine learning.

Abstract:

Malware is any type of computer software harmful to computers and networks. The amount of malware is

increasing every year and poses as a serious global security threat. Signature-based detection is the most

broadly used commercial antivirus method, however, it fails to detect new and previously unseen malware.

Supervised machine-learning models have been proposed in order to solve this issue, but the usefulness of

supervised learning is far to be perfect because it requires a signiﬁcant amount of malicious code and benign

software to be identiﬁed and labelled in beforehand. In this paper, we propose a new method that adopts a

collective learning approach to detect unknown malware. Collective classiﬁcation is a type of semi-supervised

learning that presents an interesting method for optimising the classiﬁcation of partially-labelled data. In this

way, we propose here, for the ﬁrst time, collective classiﬁcation algorithms to build different machine-learning

classiﬁers using a set of labelled (as malware and legitimate software) and unlabelled instances. We perform

an empirical validation demonstrating that the labelling efforts are lower than when supervised learning is

used, while maintaining high accuracy rates.

1 INTRODUCTION

Commercial anti-malware solutions are based on sig-

nature databases for the detection of known malicious

executables (Morley, 2001). However, there are sev-

eral problems that make the signature-based methods

less than completely reliable: ﬁrst they cannot cope

with code obfuscations and second cannot detect pre-

viously unseen malware. In this paper, we are going

to focus on the second problem: detecting previously

unseen malware.

Machine-learning-based approaches train classiﬁ-

cation algorithms that detect new malware (this type

of malware is usually called ‘in the wild’ by the anti-

malware industry and research community), relying

on datasets composed of several characteristic fea-

tures of both malicious and benign software. Schultz

et al. (Schultz et al., 2001) were the ﬁrst to intro-

duce the concept of applying machine-learning algo-

rithms for the detection of malware based on their re-

spective binary codes. They applied different clas-

siﬁers to three types of feature sets: (i) program

headers, (ii) strings and (iii) byte sequences. Later,

Kolter et al. (Kolter and Maloof, 2004) improved

Schulz’s results by applying n-grams (i.e., overlap-

ping byte sequences) instead of non-overlapping se-

quences. This approach employed several algorithms,

achieving the best results with a boosted

decision

tree. Substantial research has focused on n-gram dis-

tributions of byte sequences and machine-learning al-

gorithms (Moskovitch et al., 2008; Zhou and Inge,

2008; Santos et al., 2009).

Nevertheless, machine-learning classiﬁers require

a high number of labelled executables for each of the

classes (i.e., malware and benign). It is quite difﬁcult

to obtain this amount of labelled data for a real-world

problem such as the malicious code analysis. To gen-

erate these data, a time-consuming process of analysis

is mandatory and, in the process, some malicious exe-

cutables can avoid detection. Within the full scope of

machine-learning, several approaches have been pro-

posed to deal with this issue. Semi-supervised learn-

ing is a type of machine-learning technique that is

specially useful when a limited amount of labelled

data exists for each class (Chapelle et al., 2006).

In particular, collective classiﬁcation (Neville and

Jensen, 2003) is an approach that uses the relational

Boosting is a machine-learning technique that builds a

strong classiﬁer composed of a high number of weak clas-

siﬁers (Schapire, 2003).

251

Santos I., Laorden C. and G. Bringas P..

COLLECTIVE CLASSIFICATION FOR UNKNOWN MALWARE DETECTION.

DOI: 10.5220/0003452802510256

In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2011), pages 251-256

ISBN: 978-989-8425-71-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

structure of the combined labelled and unlabelled

data-set to enhance classiﬁcation accuracy. With re-

lational approaches, the predicted label of an example

will often be inﬂuenced by the labels of related ex-

amples. The idea behind collective classiﬁcation is

that the predicted labels of a test-example should also

be inﬂuenced by the predictions made for the related

test-examples. In some cases, it is interesting to de-

termine the topic of not just a single evidence, but to

infer it for a collection of unlabelled evidences. Col-

lective classiﬁcation tries to collectively optimise the

problem taking into account the connections present

among the executables’ machine code. This is a semi-

supervised technique, i.e., uses both labelled and un-

labelled data – typically a small amount of labelled

data and a large amount of unlabelled data – that re-

duces the labelling work.

Given this background, in a previous work (San-

tos et al., 2011), we proposed the adoption of LLGC,

a semi-supervised approach, for malware detection.

Here, we propose the ﬁrst approach that employs col-

lective classiﬁcation algorithms for the detection of

unknown malware that improves our previous results.

These methods are able to learn from both labelled

and unlabelled data. For the representation of ex-

ecutables, we chose the byte n-gram distribution, a

well-known technique that has achieved signiﬁcant

results with supervised machine learning (Kolter and

Maloof, 2004; Moskovitch et al., 2008; Santos et al.,

2009; Devesa et al., 2010). However, the presented

collective methodology is scalable to any representa-

tion susceptible to be represented as a feature vector.

Summarising, our main ﬁndings in this paper are:

(i) we describe how to adopt collective classiﬁcation

for unknown malware detection, (ii) we determine

the optimal number of labelled instances and evalu-

ate how this parameter affects the ﬁnal accuracy of

the models and (iii) we show that labelling efforts can

be reduced in the industry, while still maintaining a

high rate of accuracy.

2 BYTE N-GRAM

REPRESENTATION

Byte n-grams frequencies distribution is a well-

known approach for training machine-learning classi-

ﬁers to detect unknown malicious code (Schultz et al.,

2001; Kolter and Maloof, 2004; Moskovitch et al.,

2008; Shaﬁq et al., 2008; Zhou and Inge, 2008; San-

tos et al., 2009). To obtain a representation of the

executables by the use of byte n-grams, we need to

extract every possible sequence of bytes and their ap-

pearance frequency.

Speciﬁcally, a binary program P can be rep-

resented as a sequence of ℓ bytes b as P =

,...,b

ℓ−1

ℓ

}. A byte n-gram sequence g

is deﬁned as a subset of consecutive bytes within an

executable ﬁle where g ⊆ P and it is made up of

bytes b, such as g = (b

,...,b

n−1

) where

n is the length of the byte n-gram g. Therefore,

a program P is composed of byte n-grams such as

P = (g

,...,g

ℓ−1

ℓ

) where ℓ is the total number

of possible n-grams of a ﬁxed length n.

We use ‘term frequency - inverse document fre-

quency’ (t f − id f) (McGill and Salton, 1983) to ob-

tain the weight of each byte n-gram, whereas the

weight of the i

n-gram in the j

executable, denoted

by weight(i, j), is deﬁned by: weight(i, j) = t f

i, j

·id f

where the term frequency t f

i, j

(McGill and Salton,

1983) is deﬁned as: t f

i, j

∑

k, j

where m

i, j

is the

number of times the n-gram t

i, j

appears in an exe-

cutable e, and

∑

k, j

is the total number of n-grams

in the executable e.

On the other hand, the inverse document fre-

quency id f

is deﬁned as: id f

|E |

|E :t

∈e|

where |E |

is the total number of executables and |E : t

∈ e| is

the number of executables containing the n-gram t

Finally, we can obtain a vector ~v com-

posed of byte n-grams frequencies, ~v =

((g

,weight

),...,(g

m−1

,weight

m−1

),(g

, weight

)),

where g

is the byte n-gram and weight

is the value

of t f − id f for that particular n-gram.

3 COLLECTIVE

CLASSIFICATION

Collective classiﬁcation is a combinatorial optimiza-

tion problem, in which we are given a set of doc-

uments, or nodes, D = { d

,...,d

} and a neigh-

bourhood function N, where N

⊆ D \ {D

}, which

describes the underlying network structure (Namata

et al., 2009). Being D a random collection of docu-

ments, it is divided into two sets X and Y where X

corresponds to the documents for which we know the

correct values and Y are the documents whose val-

ues need to be determined. Therefore, the task is to

label the nodes Y

∈ Y with one of a small number

of labels, L = {l

,...,l

}. We use the Waikato En-

vironment for Knowledge Analysis (WEKA) (Garner,

1995) and its Semi-Supervised Learning and Collec-

tive Classiﬁcation plugin

which provides the follow-

ing collective classiﬁers:

Available at: http://www.scms.waikato.ac.nz/~fracpete/

projects/collectiveclassiﬁcation

SECRYPT 2011 - International Conference on Security and Cryptography

252

• CollectiveIBk: It uses internally WEKA’s classic

IBk algorithm, implementation of the K-Nearest

Neighbour (KNN), to determine the best k on the

training set and builds then, for all instances from

the test set, a neighbourhood consisting of k in-

stances from the pool of train and test set (either a

na¨ıve search over the complete set of instances or

a k-dimensional tree is used to determine neigh-

bours), which are sorted according to their dis-

tance to the test instance they belong to. For every

unlabelled test instance with the highest rank, the

class label is determined by majority vote. This

is performed until no further unlabelled test in-

stances remain. The classiﬁcation terminates by

returning the class label of the instance that is

about to be classiﬁed.

• CollectiveForest: It uses WEKA’s implementa-

tion of RandomTreeas base classiﬁer to divide the

test set into folds containing the same number of

elements. The ﬁrst iteration trains using the orig-

inal training set and generates the distribution for

all the instances in the test set. The best instances

are then added to the original training set (being

the number of instances chosen the same as in a

fold). The next iterations train with the new train-

ing set and generate then the distributions for the

remaining instances in the test set.

• CollectiveWoods & CollectiveTree: Collective-

Woods works like CollectiveForest using Collec-

tiveTree instead of RandomTree. Collective tree

splits the attribute at that position that divides the

current subset of instances (training and test in-

stances) into two halves. The process ﬁnishes if

one of the following conditions is met: (i) only

training instances would be covered (the labels

for these instances are already known), (ii) only

test instances in the leaf, case in which distribu-

tion from the parent node is taken and (iii) only

training instances of one class, case in which all

test instances are considered to have this class. To

calculate the class distribution of a complete set

or a subset, the weights are summed up according

to the weights in the training set, and then nor-

malised. The nominal attribute distribution corre-

sponds to the normalised sum of weights for each

distinct value and, for the numeric attribute, distri-

bution of the binary split based on median is cal-

culated and then the weights are summed up for

the two bins and ﬁnally normalised.

• RandomWoods: It works like WEKA’s classic

RandomForest but using CollectiveBagging (clas-

sic Bagging, a machine learning ensemble meta-

algorithm to improve stability and classiﬁcation

accuracy, extended to make it available to col-

lective classiﬁers) in combination with Collec-

tiveTree in contrast to RandomForest, which uses

Bagging and RandomTree.

4 EXPERIMENTAL RESULTS

The research question we seek to answer through this

empirical validation is the following one: What is the

minimum number of labelled instances required to as-

sure a suitable performance using collective classi-

ﬁcation? To this end, we collected a dataset com-

prising 1,000 malicious executables and 1,000 benign

ones. For the malware, we gathered random samples

from the website VxHeavens

, which has assembled

a malware collection of more than 17,000 malicious

programs, including 585 malware families that repre-

sent different types of current malware such as Tro-

jan horses, viruses and worms. Although they had al-

ready been labelled according to their family and vari-

ant names, we analysed them using Eset Antivirus

conﬁrm this labelling. For the benign dataset, we col-

lected legitimate executables from our own comput-

ers. We also performed an analysis of the benign ﬁles

using Eset Antivirus to conﬁrm their legitimacy.

By means of this dataset, we conducted the fol-

lowing methodology to answer the research question

and thus, evaluate the proposed method:

1. Byte N-gram Extraction. We extracted the byte

n-gram representation for each ﬁle in the dataset

for n = 2. This speciﬁc length was chosen because

it is the number of bytes that an operation repre-

sented by an operational code needs in machine

code, a widely-used n-gram length in the literature

(Schultz et al., 2001; Kolter and Maloof, 2004).

2. Feature Extraction. Because the total number

of features we obtained was high, we applied a

feature selection step based on a Document Fre-

quency (DF) measure, which counts the number

of documents in which a speciﬁc n-gram appears,

selecting the 5,000 top ranked byte n-grams. This

concrete number of features was chosen because

it provides a balance between efﬁciency and ac-

curacy and it has been proven to be effective

(Moskovitch et al., 2008).

3. Training and Test Generation. We constructed

an ARFF ﬁle (Holmes et al., 1994) (i.e., At-

tribute Relation File Format) with the resultant

vector representations of the executables to build

the aforementioned WEKA’s classiﬁers. Next,

Available at: http://vx.netlux.org/

Available at: http://www.eset.com/

COLLECTIVE CLASSIFICATION FOR UNKNOWN MALWARE DETECTION

253

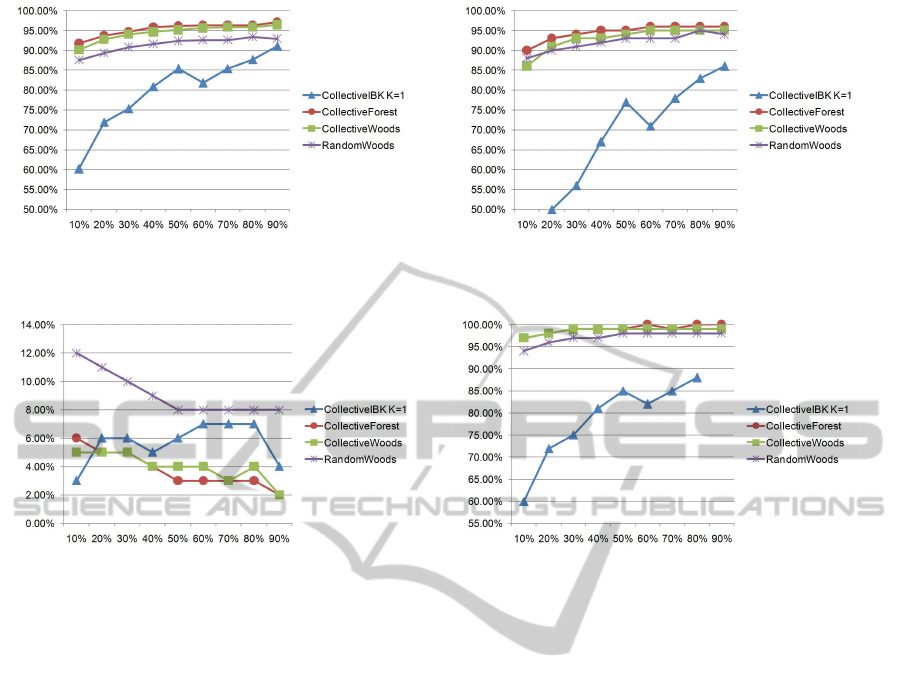
(a) Accuracy results. The X axis represents the amount of labelled

data (training dataset) whereas the Y axis represents the accuracy

of the different collective classiﬁers.

(b) TPR results. The X axis represents the amount of labelled

data (training dataset) whereas the Y axis represents the TPR of

the different collective classiﬁers.

data (training dataset) whereas the Y axis represents the FPR of

the different collective classiﬁers.

(d) AUC results. The X axis represents the amount of labelled

data (training dataset) whereas the Y axis represents the AUC of

the different collective classiﬁers.

Figure 1: The results of our collective-classiﬁcation-based malware detection method. Collective Forest was the classiﬁer

with the highest accuracy, TPR and AUC, and the lowest value of FPR. Our results outline that, obviously, the higher the

number of labelled executables are in the dataset the better results are achieved.

we split the dataset into different percentages of

training and tested instances. In other words, we

changed the number of labelled instances from

10% to 90% to measure the effect of the num-

ber of labelled instances on the ﬁnal performance

of collective classiﬁcation in detecting unknown

malware. In particular, we used the collective

classiﬁcation implementations provided by the

Semi-Supervised Learning and Collective Clas-

siﬁcation package for the well-known machine-

learning tool WEKA (Garner, 1995). All the clas-

siﬁers were tested with their default parameters.

4. Testing the Models. To test the approach, we

measured the True Positive Ratio (TPR), i.e., the

number of malware instances correctly detected

divided by the total number of malware ﬁles:

TPR = (TP)/(TP+ FN) where TP is the number

of malware cases correctly classiﬁed (true posi-

tives) and FN is the number of malware cases

misclassiﬁed as legitimate software (false nega-

tives). We also measured the False Positive Ra-

tio (FPR), i.e., the number of benign executa-

bles misclassiﬁed as malware divided by the total

number of benign ﬁles: FPR = (FP)/(FP+ TN)

where FP is the number of benign software cases

incorrectly detected as malware and TN is the

number of legitimate executables correctly clas-

siﬁed. Furthermore, we measured accuracy, i.e.,

the total number of hits of the classiﬁers divided

by the number of instances in the whole dataset:

Accuracy = (TP + TN)/(TP + FP + TP + TN)

Finally, we measured the Area Under the ROC

Curve (AUC), which establishes the relation be-

tween false negatives and false positives (Singh

et al., 2009). The ROC curve is obtained by plot-

ting the TPR against the FPR. All the these mea-

sures refer to the test instances.

Figure 1 shows the obtained results in terms of ac-

curacy, AUC, TPR and FPR. Figure 1(a) shows the ac-

curacy results of our proposed method. As one may

think in beforehand, the higher the number of train-

ing instances the higher the accuracy of the different

models. In particular, the best overall results were ob-

tained by Collective Forest, achieving results higher

than 90% for every possible conﬁguration and higher

than 95% when half of the instances were used for

SECRYPT 2011 - International Conference on Security and Cryptography

254

training. On the other hand, Collective IBK obtained

the lowest accuracy results, achieving an accuracy

higher than 80% only when more than the 50% of the

instances were employed. Figure 1(b) shows the ob-

tained results in terms of correctly classiﬁed malware

executables. Collective Forest was also the best, de-

tecting more than the 90% of the malware executables

for every tested conﬁguration. Figure 1(c) shows the

FPR results. Every classiﬁer obtained results lower

than the 10%. In particular, the lowest FPR was of

2%, achieved by CollectiveForest using the 90% of

the instances for training. However, in order to guar-

antee results of FPR lower than 5%, Collective Forest

only needs to be trained with a minimum of 20% of

the dataset. Finally, regarding AUC (shown in Fig-

ure 1(d)), Collective Forest was the best with results

higher than 97% for every conﬁguration.

5 DISCUSSION

The obtained results validate our initial hypothesis

that building an unknown malware detector based on

collective classiﬁcation is feasible. The classiﬁers

achieved high performance in classifying unknown

malware, improving our previous results using LLGC

(Santos et al., 2011), which achieved a 86% of ac-

curacy in its best conﬁguration. Therefore, we be-

lieve that our results will have a strong impact in the

area of unknownmalware detection, which usually re-

lies on supervised machine learning (Schultz et al.,

2001; Kolter and Maloof, 2004). Training the model

through supervised machine-learning algorithms can

be a problem itself because supervised learning re-

quires each instance in the dataset to be properly la-

belled. This demands a large amount of time and

resources. We have dealt with this problem by us-

ing a collective approach that only needs a certain

amount of data to be labelled. In this way, we tried

to ﬁnd among our results the number of labelled mal-

ware that is needed to assure a certain performance in

unknown malware detection. In particular, we found

out that if we label the 10% of the the total corpus,

our method can achieve an accuracy and a F-measure

greater than 90%. Nevertheless, there are several con-

siderations regarding the viability of this method.

First, because of the static nature of the proposed

method, it cannot counter packed malware. Packed

malware is the result of cyphering the payload of the

executable and deciphering it when the executable is

ﬁnally loaded into memory. One solution to solve this

obvious limitation of our malware detection method is

the use of a generic dynamic unpacking schema such

as PolyUnpack (Royal et al., 2006), Renovo (Kang

et al., 2007), OmniUnpack (Martignoni et al., 2007)

or Eureka (Sharif et al., 2008). These methods exe-

cute the sample in a contained environment and ex-

tract the actual payload, allowing further static or dy-

namic analysis of the executable.

Second, our method can be considered as a statis-

tical representation of executables. Therefore, an at-

tacker can surpass this method of detection by adding

several ‘good’ byte sequences. For example, in the

ﬁeld of spam ﬁltering (spam is deﬁned as unsolicited

bulk mail), Good Word Attack is a method that mod-

iﬁes the term statistics by appending a set of words

that are characteristic of legitimate e-mails, thereby

bypass spam ﬁlters. Nevertheless, we can adapt to this

malware detector some of the methods that have been

proposed in order to improve spam ﬁltering , such as

Multiple Instance Learning (MIL) (Zhou et al., 2007).

MIL will divide an executable or a vector in the tra-

ditional methods into several sub-instances and will

classify the original vector or classiﬁer based on the

sub-instances.

Finally, in our experiments, we used a training

dataset that is very small in comparison to commercial

antivirus databases. Whenever the dataset size grows,

the issue of scalability becomes a concern. This

problem produces excessive storage requirements, in-

creases time complexity and impairs the general ac-

curacy of the models (Cano et al., 2006). To reduce

disproportionate storage and time costs, it is neces-

sary to reduce the size of the original training set

(Czarnowski and Jedrzejowicz, 2006). To solve this

issue, data reduction is normally considered an ap-

propriate preprocessing optimisation technique (Pyle,

1999; Tsang et al., 2003). Data reduction can be im-

plemented in two ways. Instance selection (IS) seeks

to reduce the number of evidences (i.e., number of

rows) in the training set by selecting the most rele-

vant instances or by re-sampling new ones (Liu and

Motoda, 2001). Feature selection (FS) decreases the

number of attributes or features (i.e., columns) in the

training set (Liu and Motoda, 2008).

Future work will be oriented on three main di-

rections. First, we will extend our study of collec-

tive learning by applying more algorithms to this is-

sue. Second, we will use different features for train-

ing these kind of models. Third, we will face packed

executables with a hybrid dynamic-static approach.

REFERENCES

Cano, J., Herrera, F., and Lozano, M. (2006). On the combi-

nation of evolutionary algorithms and stratiﬁed strate-

gies for training set selection in data mining. Applied

Soft Computing Journal, 6(3):323–332.

COLLECTIVE CLASSIFICATION FOR UNKNOWN MALWARE DETECTION

255

Chapelle, O., Sch¨olkopf, B., and Zien, A. (2006). Semi-

supervised learning. MIT Press.

Czarnowski, I. and Jedrzejowicz, P. (2006). Instance reduc-

tion approach to machine learning and multi-database

mining. In Proceedings of the Scientiﬁc Session orga-

nized during XXI Fall Meeting of the Polish Informa-

tion Processing Society, Informatica, ANNALES Uni-

versitatis Mariae Curie-Skłodowska, Lublin, pages

60–71.

Devesa, J., Santos, I., Cantero, X., Penya, Y. K., and

Bringas, P. G. (2010). Automatic Behaviour-based

Analysis and Classiﬁcation System for Malware De-

tection. In Proceedings of the 12

International Con-

ference on Enterprise Information Systems (ICEIS),

pages 395–399.

Garner, S. (1995). Weka: The Waikato environment for

knowledge analysis. In Proceedings of the New

Zealand Computer Science Research Students Confer-

ence, pages 57–64.

Holmes, G., Donkin, A., and Witten, I. H. (1994). Weka: a

machine learning workbench. pages 357–361.

Kang, M., Poosankam, P., and Yin, H. (2007). Renovo:

A hidden code extractor for packed executables. In

Proceedings of the 2007 ACM workshop on Recurring

malcode, pages 46–53.

Kolter, J. and Maloof, M. (2004). Learning to detect ma-

licious executables in the wild. In Proceedings of

the 10

ACM SIGKDD international conference on

Knowledge discovery and data mining, pages 470–

478. ACM New York, NY, USA.

Liu, H. and Motoda, H. (2001). Instance selection and con-

struction for data mining. Kluwer Academic Pub.

Liu, H. and Motoda, H. (2008). Computational methods of

feature selection. Chapman & Hall/CRC.

Martignoni, L., Christodorescu, M., and Jha, S. (2007).

Omniunpack: Fast, generic, and safe unpacking of

malware. In Proceedings of the 23

Annual Com-

puter Security Applications Conference (ACSAC),

pages 431–441.

McGill, M. and Salton, G. (1983). Introduction to modern

information retrieval. McGraw-Hill.

Morley, P. (2001). Processing virus collections. In Proceed-

ings of the 2001 Virus Bulletin Conference (VB2001),

pages 129–134. Virus Bulletin.

Moskovitch, R., Stopel, D., Feher, C., Nissim, N., and

Elovici, Y. (2008). Unknown malcode detection via

text categorization and the imbalance problem. In

Proceedings of the 6

IEEE International Conference

on Intelligence and Security Informatics (ISI), pages

156–161.

Namata, G., Sen, P., Bilgic, M., and Getoor, L. (2009). Col-

lective classiﬁcation for text classiﬁcation. Text Min-

ing, pages 51–69.

Neville, J. and Jensen, D. (2003). Collective classiﬁca-

tion with relational dependency networks. In Proceed-

ings of the Workshop on Multi-Relational Data Min-

ing (MRDM).

Pyle, D. (1999). Data preparation for data mining. Morgan

Kaufmann.

Royal, P., Halpin, M., Dagon, D., Edmonds, R., and Lee,

W. (2006). Polyunpack: Automating the hidden-code

extraction of unpack-executing malware. In Proceed-

ings of the 22

Annual Computer Security Applica-

tions Conference (ACSAC), pages 289–300.

Santos, I., Nieves, J., and Bringas, P. (2011). Semi-

supervised learning for unknown malware detection.

In Abraham, A., Corchado, J., Gonzlez, S., and

De Paz Santana, J., editors, International Symposium

on Distributed Computing and Artiﬁcial Intelligence,

volume 91 of Advances in Intelligent and Soft Com-

puting, pages 415–422. Springer Berlin / Heidelberg.

Santos, I., Penya, Y., Devesa, J., and Bringas, P. (2009).

N-Grams-based ﬁle signatures for malware detection.

In Proceedings of the 11

International Conference

on Enterprise Information Systems (ICEIS), Volume

AIDSS, pages 317–320.

Schapire, R. (2003). The boosting approach to machine

learning: An overview. Lecture Notes in Statistics,

pages 149–172.

Schultz, M., Eskin, E., Zadok, F., and Stolfo, S. (2001).

Data mining methods for detection of new malicious

executables. In Proceedings of the 22

d IEEE Sympo-

sium on Security and Privacy., pages 38–49.

Shaﬁq, M., Khayam, S., and Farooq, M. (2008). Embedded

Malware Detection Using Markov n-Grams. Lecture

Notes in Computer Science, 5137:88–107.

Sharif, M., Yegneswaran, V., Saidi, H., Porras, P., and Lee,

W. (2008). Eureka: A Framework for Enabling Static

Malware Analysis. In Proceedings of the European

Symposium on Research in Computer Security (ES-

ORICS), pages 481–500.

Singh, Y., Kaur, A., and Malhotra, R. (2009). Compara-

tive analysis of regression and machine learning meth-

ods for predicting fault proneness models. Interna-

tional Journal of Computer Applications in Technol-

ogy, 35(2):183–193.

Tsang, E., Yeung, D., and Wang, X. (2003). OFFSS: op-

timal fuzzy-valued feature subset selection. IEEE

transactions on fuzzy systems, 11(2):202–213.

Zhou, Y. and Inge, W. (2008). Malware detection using

adaptive data compression. In Proceedings of the 1st

ACM workshop on Workshop on AISec, pages 53–60.

ACM New York, NY, USA.

Zhou, Y., Jorgensen, Z., and Inge, M. (2007). Combating

Good Word Attacks on Statistical Spam Filters with

Multiple Instance Learning. In Proceedings of the 19

IEEE International Conference on Tools with Artiﬁ-

cial Intelligence-Volume 02, pages 298–305.

SECRYPT 2011 - International Conference on Security and Cryptography

256