COMPREHENSIBLE MODEL OF AMPLITUDE

NONLINEARITIES IN PIEZORESISTIVE-FORCE SENSORS

L. Paredes-Madrid and P. Gonzalez de Santos

Centre for Automation and Robotics UPM-CSIC, Ctra. Campo Real Km 0,2, 28500 Arganda del Rey, Madrid, Spain

Keywords: Piezoresistive, force, Sensor, Nonlinear, Model, Tanh, Piezocapacitive, Flexiforce.

Abstract: This article upgrades the RC linear model presented for the piezoresistive-force sensors. Amplitude

nonlinearity was found in sensors conductance, and a characteristic equation was formulated for modeling

it. By using such equation, it is possible to determine sensor sensitivity for any driving voltage below 1V.

This model considerable improves the plug-and-play capability of the sensor. However, sensor conductance

is unsatisfactory modeled by such equation when the input voltage goes over 1V. We present an approach

for such driving condition.

1 INTRODUCTION

Piezoresistive force sensors have demonstrated to be

a good solution for applications demanding non-

invasive force readings (Kong et al., 2008; Monroy

et al., 2009). However, the relative low repeatability

and considerable hysteresis of such sensors,

compared to load cells (Vecchi et al., 2000), limit

their use to applications where accuracy is not as

relevant as the size of the sensor involved (Lebosse

et al., 2008).

On the other hand, load cells have demonstrated

to be a trustable-force-measurement device in many

different systems (Muller et al., 2010) demanding

high reliability and accuracy, i.e., force control

applications (Sijs et al., 2008) and rehabilitation

(Goto et al., 2005). There are several reasons,

besides high repeatability, for using load cells: they

are available in different sizes and force ranges, they

can perform force readings in multiple axes and can

withstand overload forces without suffering

damages. Dynamic response of load cells is also

exceptional, while exhibiting negligible time drift.

The main disadvantages of load cells are based in

their large bulk and heavy weight, requiring that

when a new robot or force control system is under

design, load-cell bulk and weight must be taken into

account from the early stages of design, since load-

cell mass is usually comparable with the system

mass where it is used.

In certain research fields as biomechanics,

biomedical engineering and haptics, it is necessary

to perform non-invasive force readings which are

not possible to carry out by using the

abovementioned-bulky load cells. Whether if it is

necessary to measure contact force on a knee joint

(Sawaguchi et al., 2009), or measure grasp force of a

human hand (Castro & Cliquet Jr, 2002), within

many other applications (Kazerooni et al., 2005;

Ahroni et al., 1998), a low profile, light-weight

sensor must be used in order to meet the limited

space requirements of the task. Piezoresistive force

sensors are the best solution since they can be fitted

in many applications without requiring substantial

changes in the mechanical layout. However, as

mentioned previously, they lack of good

repeatability and exhibit considerable hysteresis

compared to load cells. We are interested in

improving piezoresistive-sensors performance with

the aim of using them in tele-operation devices

specially those devoted to remote handling activities

for the maintenance and repair of nuclear fusion

installations (Ibarra et al., 2010)

Previous works (Paredes-Madrid, Torruella et al.,

2010; Paredes-Madrid, Emmi et al., 2010) have

demonstrated that the repeatability of piezoresistive

force sensor may be increased by performing

capacitance readings under AC sourcing. The

method detailed in (Paredes-Madrid, Torruella et al.,

2010) consists in reading sensor’s conductance and

capacitance by applying DC and sine waveforms,

thereby; it is possible to perform a multivariable

estimation of force which dramatically reduces force

estimation errors.

In (Paredes-Madrid, Emmi et al., 2010), a RC-

parallel-electrical model was identified for the

405

Paredes-Madrid L. and Gonzalez de Santos P..

COMPREHENSIBLE MODEL OF AMPLITUDE NONLINEARITIES IN PIEZORESISTIVE-FORCE SENSORS.

DOI: 10.5220/0003453604050410

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 405-410

ISBN: 978-989-8425-74-4

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Piezoresistive Force Sensor (PFS) model

FlexiForce® A201-100, also, the sensor exhibited a

nonlinear response when the frequency of the

driving signal went over a determined limit

conveniently named as the divergent frequency.

However, we have recently found that the sensor

exhibits additional nonlinearities related with the

amplitude of the driving signal, and thus the RC

model and the corresponding equations must be

adjusted to embrace the newly-found-amplitude

nonlinearity.

This paper reviews the RC model for the A201-

100 force sensor which will be referred from now on

as PFS. This device was chosen for the study

because the manufacturer has developed many

specific sensor for research (Culjat et al., 2008),

medical (R. A. Lee et al., 2009) industrial and

service tasks (Tekscan, 2011), but the results here

reported are extendable to other similar devices.

Later, amplitude nonlinearity is identified in the

sensor and an equation is deducted from

experimental data. The feasibility of such equation

for modeling sensor conductance is fully tested and

demonstrated for driving voltages below 1V.

However, it is shown later that the model becomes

unsuitable when the sourcing voltage goes over 1V,

and so, it is presented an approach for modeling

sensor conductance under such driving condition.

2 REVIEW OF THE RC MODEL

FOR THE PFS

Previously, the PFS from Fig. 1a was characterized

in terms of frequency and transient response to

input-sine waves and square waves, respectively.

Test results yielded to a RC-parallel-electrical model

(see Fig. 1b) for the PFS and consequently a set of

equations were presented to model its behavior;

however, when the frequency of the driving signal

went over a determined value, conveniently named

as the divergent point, sensor resistance started to

drop as frequency was increased, and the RC model

became no longer valid.

a b c

Figure 1: Piezoresistive sensor under study. (a) Picture of

the PFS (b) Electrical model of the PFS. (c) Conditioning

circuit for measuring forces in the PFS.

This behavior splits sensor response in two

differentiated regions: one linear region, when

operating below the divergence frequency, where we

can model and predict sensor response in terms of

phase shift and output amplitude according to the

RC theoretical equations, and a nonlinear region,

when operating over the divergent frequency, where

phase shift and output amplitude become

unpredictable.

The typical driving circuit for the PFS is depicted

in Fig. 1c. When the sine wave, V

, is selected as

input; the following set of equations taken from

(Paredes-Madrid, Torruella et al., 2010) describes

sensor response within its linear region of operation.

First, a differential equation can be deduced from

the circuit depicted in Fig. 1c with V

as input:

VdVV

dt R

+=−

(1)

where R

and C

are sensor Resistance and

Capacitance respectively from the model in Fig.1b,

is the feedback resistor in the driving circuit of

Fig. 1c with V

as the output voltage. Given the

input:

(

)

sin 2

VA ft

(2)

The output voltage, V

, can be expressed as:

(

)

()

sin 2

-2cos2

osg s

VAR fC ft

ππ

⎛⎞

⎜⎟

⎝⎠

(3)

Second, equation (3) may be rewritten in terms

of phase shift, θ, and output amplitude, A

, as below:

(

)

sin 2

VA ft

(4)

At last, joining (3) and (4) result in:

cos( )

(5)

()

Asin

(6)

Equation (6) was previously used in (Paredes-

Madrid, Torruella et al., 2010) to measure

capacitance changes as force increases. This yielded

to demonstrate that the PFS exhibits a

piezocapacitive property which is useful for

reducing force estimation errors.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

406

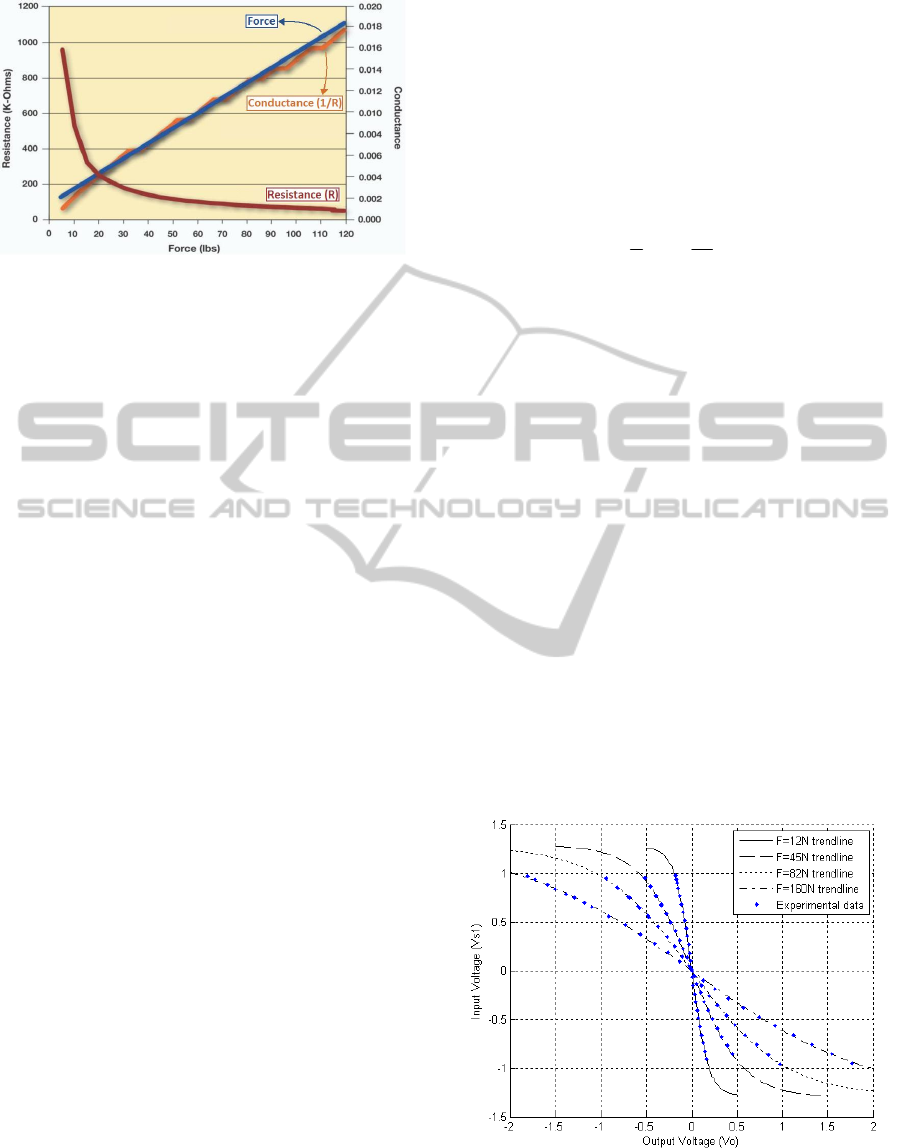
Figure 2: Typical variation of resistance and conductance

for an A201-100 FlexiForce® Sensor, image taken from

(Tekscan, 2009a). The image legend was modified for

better comprehension.

3 AMPLITUDE NONLINEARITY

OF THE PFS UNDER DC

SOURCING

Besides the already identified frequency

nonlinearity, the PFS exhibits amplitude

nonlinearity. Initially, we only study such

nonlinearity for input voltages within the range

(-1V, 1V), and then we present an approach for

higher input voltages. The analysis of amplitude

nonlinearity must be split in two because the sensor

exhibits quasi-different responses depending on the

input voltage applied.

3.1 Modelling Amplitude Nonlinearity

for Input Voltages below 1V

If we choose the DC source, V

, as the input of the

driving circuit in Fig. 1c we obtain a DC output

voltage, V

, which changes linearly, see Fig. 2

(Tekscan Inc, 2009a) , as the applied force on the

sensor increases. This response has been thorough

described by sensor manufacturer (Tekscan Inc,

2009b) and in many research articles (Lebosse et al.,

2008; Vecchi et al., 2000); this behavior corresponds

to the piezoresistive property of the sensor.

However, to our knowledge, there is not information

available about how the output voltage changes, for

a fixed force, when the DC voltage is varied.

In order to study such behavior, we swept the

input voltage, V

, starting at -1V up to 1V and plot

de output voltage, V

, while keeping constant the

applied force. In practice, the voltage sweep was

made by sourcing the sensor with a low frequency

triangle signal of 0.4Hz with peak amplitude of 1V

and no offset. The frequency must be kept as low as

possible in order to avoid phase-lag effects due to

the built-in-sensor capacitance. Forces within the

range from 0N to 250N were applied to one PFS

device while the output voltage, V

was recorded.

Figure 3 shows the output voltage for randomly

chosen forces of 12N, 45N, 82N and 160N. We have

found that the best function that relates the input

voltage, V

, to the corresponding sensor response,

, is:

atanh( )

=−

(7)

where k and q are constants. However, it is not

convenient to fit k and q in the form presented in (7)

because it may yield to complex values in V

, since

the atanh domain is restricted to (-1, 1). Thus, it is

better, for fitting purposes, to rewrite (7) in terms of

the tanh function as below:

tanh( )

Vk qV=−

(8)

The minus sign in (7) and (8) comes from the

negative gain in the inverting amplifier (see Fig. 1c)

which is used to drive the sensor. The axes in Fig. 3

are intentionally switched to represent: V

in the x-

axis and V

in the y-axis with the aim of fitting the

data points with (8) instead of with (7). The fitting

process is highly confident with a coefficient of

determination, R

, of at least R

=0.9992 for every

applied force and an average value of R

=0.9995.

Parameters k and q were set to adjust

independently for every applied force; however, the

independent fitting processes returned values of k

almost constant regardless of the exerted force, F,

Figure 3: V

vs. V

for the PFS for driving voltages below

1V and four different-exerted forces of 12N, 45N, 82N

and 160N. The trendline used for each individual fit was a

hyperbolic tangent function (8).

COMPREHENSIBLE MODEL OF AMPLITUDE NONLINEARITIES IN PIEZORESISTIVE-FORCE SENSORS

407

whereas q has shown to be hyperbolically dependant

on the exerted force; in other words, 1/q is a linear

function of F. Figure 4 show the variation of k and

1/q for different applied forces within the range from

0N to 250N resulting from independent-fitting

processes.

Several facts may be taken out from Fig. 3 and

Fig. 4 but first, it is necessary to relate (8) with F in

order to get a whole view of sensor behavior. For

such purpose, we must remember that the sensor

exhibits a piezoresistive behavior and thus its

conductance, 1/R

, may be modeled in terms of the

applied force, F, as:

mF b=+

(9)

Equation (9) is not explicitly stated in the PFS

datasheet (Tekscan Inc, 2009b); however, the sensor

manufacturer declares that a linear interpolation

between the conductance values and the applied

forces can be done. Also, by looking at the

conductance curve in Fig. 2, it can be easily

deducted that (9) is a valid fit for 1/R

. Considering

the inverting-amplifier, with feedback resistor R

which is used to drive the PFS, it is possible to link

(9) with the amplifier characteristic equation:

=−

(10)

to obtain:

()

mF b

=− +

(11)

We must clarify that (11) is not explicitly stated

in the PFS datasheet (Tekscan Inc, 2009b). Only

(10) is stated in (Tekscan Inc, 2009b), but the

manufacturer suggests that sensor sensitivity, m, can

be changed by either replacing the feedback resistor,

, or by changing the driving voltage, V

According to (11) we may think that changes in

produce direct-proportional changes in sensor

sensitivity, however experimental results plotted in

Fig. 3 yield to different conclusions because the

trendline used to fit the experimental data points is

not a line.

With the aim of demonstrating that (11) is an

approximate expression for fitting the data points

from Fig. 3, we take the 1/q curve from Fig. 4 and

represent it, as linearly dependent on the applied

force.

1/ qmFb

′′

(12)

The 1/q curve is analogous to the conductance

curve of Fig. 2. From now on, we refer to m’ and b’

Figure 4: Graph representing the variation of sensor

parameters

k and q for different exerted forces within the

range from 0N to 250N.

as the generalized-sensor parameters, because we

demonstrate in the next section that they can predict

sensor sensitivity for any input voltage within the

range (-1V, 1V). Equation (12) can be substituted

into (7) yielding to:

()

atanh

VmFb

′′

=− +

⎛⎞

⎜⎟

⎝⎠

(13)

Nevertheless, we can not state (13) in the same

way as (11) because the input voltage, V

, is part of

the atanh argument, but if we take only the first term

of the atanh-taylor series we yield to the following

approximate expression:

()

mF b

−

′

(14)

Equation (14) is a non-exact expression of sensor

response since it can not model amplitude

nonlinearity, likewise (11) is too. The 1/k factor, in

(14), is analogous to R

in (11), in the same way that

m is analogous to m’, b to b’ and 1/R

to 1/q. In fact,

(11) is valid if, and only if, the input voltage remains

constant during the measurement process; this

condition matches for the recommended driving

conditions by the manufacturer (Tekscan Inc,

2009b). In case V

is changed during the

measurement process, it is necessary to recalculate

the new values of m and b in order to estimate the

applied force via (11). But, since neither (11) nor

(14) account for the amplitude nonlinearity of the

PFS, the new values of m and b would be erroneous.

Instead, it is necessary to use the exact expression

(13) to correctly estimate the new sensor parameters

resulting from the new input voltage.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

408

3.2 Effect of Feedback Resistor in

Sensor Response

The effect of feedback resistor R

in the driving

circuit of Fig. 1c and consequently in (13) can be

deducted if we notice that R

only changes the

feedback gain of the amplifier without affecting

sensor current, thus, changing R

will produce

direct-proportional changes in the output voltage as

below:

()

atanh

ref

VmFb

′′

=− +

⎛⎞

⎜⎟

⎝⎠

(15)

where R

ref

is the feedback resistor used during the

characterization to obtain the values of m’, b’ and k.

In case the feedback resistor is changed after the

characterization process, the output voltage is

multiplied by the ratio R

ref

where R

is the new

feedback resistor. Replacing the feedback resistor

produces a direct-proportional change in the output

voltage because the amplifier is inherently linear,

whereas sensor resistance is not. In fact, by linking

(7), (10) and (12), we get an expression which shows

the non-linear behavior of sensor conductance to

changes in the input voltage.

()

atanh /

ssg

mF b

RVR

′′

(16)

However, note from (16) that sensor

conductance is always linear to force changes as the

manufacturer states (Tekscan Inc, 2009b) and the

Fig. 2 shows.

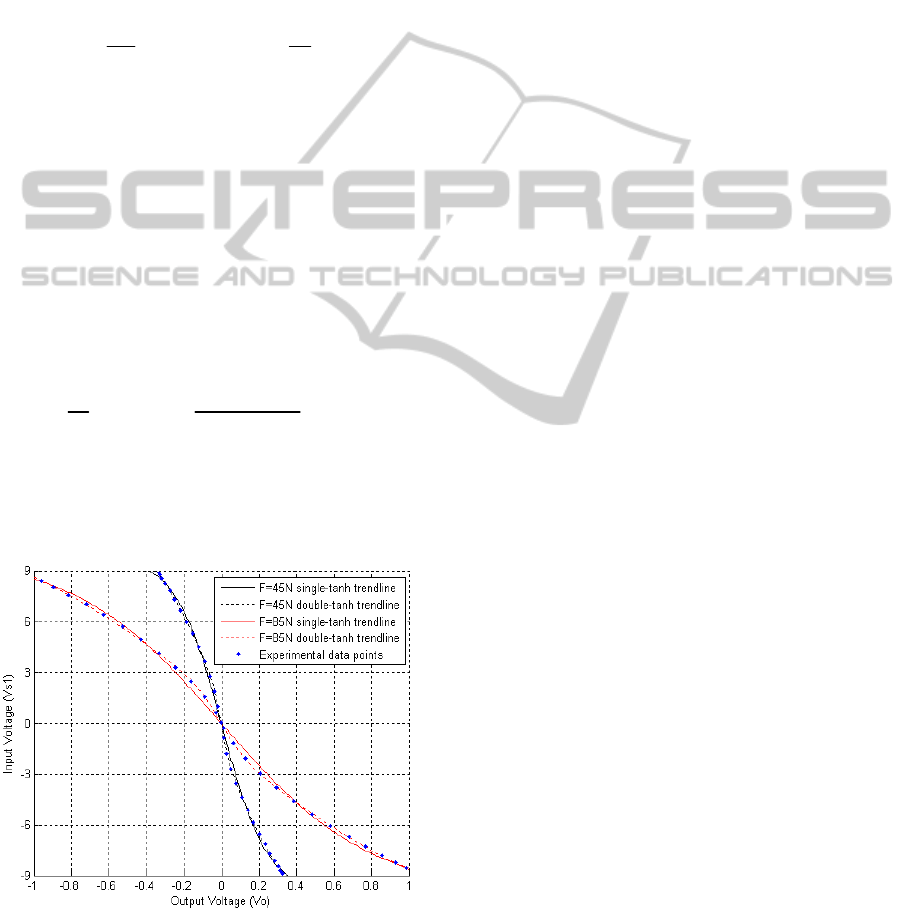
Figure 5: Graph representing the relation of V

vs. V

for

input amplitudes over 1V and forces of 45N and 85N.

Two different trendlines are shown, single (8) and double

tanh (17).

Equation (15) is the final expression we propose

for modeling sensor conductance because it accounts

for changes in V

, as well as to changes in the

feedback resistor R

. By using (15) it is possible to

estimate sensor sensitivity under any driving

voltages below 1V, or derive an appropriate set of

driving conditions (V

and R

) to obtain a target

sensitivity in the system.

3.3 An Approach to Modeling the

Amplitude Nonlinearity for Input

Voltages over 1V

In order to study the amplitude nonlinearity for input

amplitudes over 1V, it was followed the same

procedure described in section 3.1, but now V

was

restricted to a broader range (-9V, 9V). Figure 5

shows the output and input voltages for such

condition, but only the responses for two different

forces of 45N and 85N are shown for better

comprehension.

Initially, the experimental data points were fit in

the same way as in section 3.1; this implies using (8)

as trendline, but the coefficient of determination did

not result as good as before. We propose, as an

initial approach, the following curve as a general fit

for the data points resulting from V

over 1V:

11 1 2 2

tanh( ) tanh( )

so o

Vk qVk qV=−+−

(17)

Trendlines resulting from (8) and (17) are both

shown in Fig. 5 for comparison purposes. Note that

the data points are pretty close to either trendline,

single (8) or double-tanh (17), but it is clear that (17)

is a better fit specially for the data points which

satisfy the condition |V

|<3V. However, in order to

use (17) as a valid model, it is necessary a more

detailed study with the aim of understanding how

the coefficients k

, k

, q

and q

change with every

exerted force.

The main problem of proposing (17) as a valid fit

for the sensor is based in the large number of

coefficients to find and thus the multiple solutions

available. We have observed that k

remains more or

less constant around 1V, whereas k

increases with

the applied force. But a consistent variation of q

and q

has not been found yet.

4 CONCLUSIONS

A comprehensive model for the conductance of

piezoresistive-force sensors has been developed and

tested for input voltages below 1V.

COMPREHENSIBLE MODEL OF AMPLITUDE NONLINEARITIES IN PIEZORESISTIVE-FORCE SENSORS

409

A nonlinear response was identified in sensor

conductance corresponding to a hyperbolic tangent

function. For voltages over 1V, an approximate

model for sensor conductance has been presented

but additional tests are required for refining and

simplifying it.

ACKNOWLEDGEMENTS

This work has been supported by Madrid

Community through the project TECHNOFUSION

(S2009/ENE-1679).

REFERENCES

Ahroni, J.H., Boyko, E. J., Forsberg, R., 1998. Reliability

of F-scan in-shoe measurements of plantar pressure.

Foot & ankle international/American Orthopaedic

Foot and Ankle Society [and] Swiss Foot and Ankle

Society, 19(10), 668.

Castro, M. C., Cliquet Jr, A., 2002. A low-cost

instrumented glove for monitoring forces during

object manipulation. Rehabilitation Engineering,

IEEE Transactions on, 5(2), pp. 140–147.

Culjat, M. O., King, C. H., Franco, M. L., Lewis, C. E.,

Bisley, J. W., et al., 2008. A tactile feedback system

for robotic surgery. En Engineering in Medicine and

Biology Society, 2008. EMBS 2008. 30th Annual

International Conference of the IEEE. pp. 1930–1934.

Goto, E., Ohnishi, K., Miyagawa, H., Saito, Y., 2005.

Field test of a force control rehabilitation system for

quantitative evaluation of the disorder in the upper

extremities. En Rehabilitation Robotics, 2005. ICORR

2005. 9th International Conference on. pp. 82–85.

Ibarra, A., Perlado, M., Aracil, R., Blanco, D., Ferre, M.,

et al., 2010. TechnoFusión, a relevant facility for

fusion technologies: The remote handling area. Fusion

Engineering and Design.

Kazerooni, H., Fairbanks, D., Chen, A., Shin, G., 2005.

The magic glove. En Robotics and Automation, 2004.

Proceedings. ICRA'04. 2004 IEEE International

Conference on. pp. 757–763.

Kong, Y. K., Lowe, B. D., Lee, S. J., Krieg, E. F., 2008.

Evaluation of handle shapes for screwdriving. Applied

Ergonomics, 39(2), pp. 191–198.

Lebosse, C., Bayle, B., de Mathelin, M., Renaud, P., 2008.

Nonlinear modeling of low cost force sensors. En

Robotics and Automation, 2008. ICRA 2008. IEEE

International Conference on. pp. 3437–3442.

Lee, R. A., van Zundert, A. A., Maassen, R. L., Willems,

R.J., Beeke, L.P., et al., 2009. Forces applied to the

maxillary incisors during video-assisted intubation.

Anesthesia & Analgesia, 108(1), 187.

Monroy, M., Ferre, M., Barrio, J., Eslava, V., Galiana, I.,

2009. Sensorized thimble for haptics applications. In

Mechatronics, 2009. ICM 2009. IEEE International

Conference on. pp. 1–6.

Muller, I., de Brito, R., Pereira, C., Brusamarello, V.,

2010. Load cells in force sensing analysis–theory and

a novel application. Instrumentation & Measurement

Magazine, IEEE, 13(1), pp. 15–19.

Paredes-Madrid, L., Emmi, L., de Santos, P., 2010.

Improving the performance of piezoresistive force

sensors by modeling sensor capacitance. En Industrial

Electronics (ISIE), 2010 IEEE International

Symposium on. Industrial Electronics (ISIE), 2010

IEEE International Symposium on. pp. 458-463.

Paredes-Madrid, L., Torruella, P., Solaeche, P., Galiana,

I., Gonzalez de Santos, P., 2010. Accurate modeling of

low-cost piezoresistive force sensors for haptic

interfaces. In Robotics and Automation (ICRA), 2010

IEEE International Conference on. pp. 1828–1833.

Sawaguchi, N., Majima, T., Ishigaki, T., Mori, N.,

Terashima, T., et al., 2009. Mobile-Bearing Total

Knee Arthroplasty Improves Patellar Tracking and

Patellofemoral Contact Stress: In Vivo Measurements

in the Same Patients. The Journal of Arthroplasty.

Sijs, J., Liefhebber, F., Romer, G.W., 2008. Combined

Position & Force Control for a robotic manipulator. En

Rehabilitation Robotics, 2007. ICORR 2007. IEEE

10th International Conference on. pp. 106–111.

Tekscan Inc, 2011. Automotive Door Mounting. Available

at: http://www.tekscan.com/automotive-door-

mounting-pressure [February 2011].

Tekscan Inc, 2009a. E-book: Force Sensors for Design.

Available at: http://www.tekscan.com/flexiforce/force-

sensors-for-design [February 2009].

Tekscan Inc, 2009b. FlexiForce®: Single Button FSR.

Available at: http://www.tekscan.com/pdf/FlexiForce-

Sensors-Manual.pdf [February 2009].

Vecchi, F., Freschi, C., Micera, S., Sabatini, A. M., Dario,

P., et al., 2000. Experimental evaluation of two

commercial force sensors for applications in

biomechanics and motor control. In 5th Ann. Conf. of

Int. FES.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

410