ESTIMATION-DECODING ON LDPC-BASED 2D-BARCODES

W. Proß

, M. Otesteanu

and F. Quint

Faculty of Electronics and Telecommunications, Politehnica University of Timisoara, Timisoara, Romania

Faculty of Electrical Engineering and Information Technology, University of Applied Sciences, Karlsruhe, Germany

Keywords:

2D-Barcode, LDPC Code, Estimation-Decoding, Hidden-Markov-Model.

Abstract:

In this paper we propose an extension of the Estimation-Decoding algorithm for the decoding of our Data

Matrix Code (DMC), which is based on Low-Density-Parity-Check (LDPC) codes and is designed for use in

industrial environment. To include possible damages in the channel-model, a Markov-modulated Gaussian

channel (MMGC) was chosen to represent everything in between the embossing of a LDPC-based DMC and

the camera-based acquisition. The MMGC is based on a Hidden-Markov-Model (HMM) that turns into a two-

dimensional model when used in the context of DMCs. The proposed ED2D-algorithm (Estimation-Decoding

in two dimensions) is implemented to operate on a 2D-LDPC-Markov factor graph that comprises of a LDPC

code’s Tanner-graph and a 2D-HMM. For a subsequent comparison between different barcodes in industrial

environment, a simulation of typical damages has been implemented. Tests showed a superior decoding be-

havior of our LDPC-based DMC decoded with the ED2D-decoder over the standard Reed-Solomon-based

DMC.

1 INTRODUCTION

In 1952 the ﬁrst barcode system was patented by J.

N. Woodland and B. Silver (Woodland and Silver,

1949). Today one dimensional barcodes are more and

more replaced by their two dimensional (2D) succes-

sors. They offer a high information-density as well

as an integrated error-correction capability in most

cases. One of the most successful 2D-barcodes is

the Data Matrix Code (DMC) which is internationally

standardized in (ISO/IEC, 2000). A DMC is formed

by the three major components, as shown in Figure

1. The ﬁnder-pattern is comprised of the solid bor-

der and the broken border. The L-shaped solid bor-

der helps in locating the DMC whereas the alternating

pattern of the broken border allows to determine the

DMC’s size. The data region contains the encoded in-

formation. Thereby a binary one is represented by a

black squared module and a binary zero by a white

squared module. This is only true if the DMC is

printed black on a white surface. When used in in-

dustrial environment the codes get stamped, milled

and laser-etched on different kinds of material. Fur-

thermore there are different kinds of interferences that

may disturb the barcode. Thereby decoding is much

more challenging.

2 LDPC-BASED DMC

Considering the application in industrial environment,

a 2D-barcode based on Low-Density-Parity-Check

(LDPC) codes was developed. The outer appearance

of our barcode is similar to that of the DMC since

the ﬁnder-pattern that surrounds a DMC has been

adopted.

PEG-LDPC Codes: The information is encoded

in our barcode by use of a regular PEG-LDPC

code unlike the standard DMC that is based on

Reed-Solomon (RS) codes. The ﬁrst introduction of

LDPC codes has already been in 1962 by Gallager

(Gallager, 1962). Since the rediscovery of LDPC

codes by MacKay and Neal in 1995 (MacKay

and Neal, 1995), many further developments have

been published, making LDPC codes a serious

competitor to RS codes and the more recent Turbo

codes for many ﬁelds of application. One important

contribution was the introduction of the Progressive-

Edge-Growth (PEG) construction of the LDPC codes

underlying Parity-Check-Matrix (Hu et al., 2005) that

made LDPC codes attractive for short block length

applications as well. A single LDPC codeword is

used to ﬁll the data region of the DMC because it is

well known that the decoding performance of LDPC

codes increases with the codeword-length.

Proß W., Otesteanu M. and Quint F..

ESTIMATION-DECODING ON LDPC-BASED 2D-BARCODES.

DOI: 10.5220/0003457400340039

In Proceedings of the International Conference on Signal Processing and Multimedia Applications (SIGMAP-2011), pages 34-39

ISBN: 978-989-8425-72-0

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Complete

Solid Border

Data Region

Broken Border

Figure 1: Three major parts of a DMC.

Symbol-placement: The procedure of placing the

LDPC codeword’s symbols within the available grid

of the DMC’s data region is done with respect to typ-

ical interferences that may occur in industrial envi-

ronment. The probability that damages caused by

dirt, rust, scratches, unequal illumination etc. affect

a contiguous part of the DMC is very high. Con-

sidering this, the symbol-nodes connected to the same

check-node in the LDPC code’s Tanner graph (Tan-

ner, 1981) are placed as far as possible from each

other in the data region under the constraint of the

limited area occupied by the code. This way each

check-node is affected by the fewest possible number

of disturbed symbol-nodes. The placement procedure

is based on an optimization process and is explained

in detail in (Proßet al., 2010). As an example, Figure 2

depicts the symbol-placement of three symbol-nodes

connected to the same check-node.

Image-processing: For the localization of the DMC,

the already known standard procedures are applied.

In contrast to the RS code used by the original DMC,

the LDPC decoder uses soft-decisions (SDs) as an in-

put. For the computation of these SDs a correlation

coefﬁcient r

i j

is calculated for each module in row i

and column j of the DMC as follows:

i j

∑

k=1

∑

l=1

i j

− ¯x

i j

)(y

− ¯y)

√

∑

k=1

∑

l=1

i j

− ¯x

i j

)

∑

k=1

∑

l=1

− ¯y)

(1)

k and l are the indices for the h horizontal and v

vertical pixels in each module respectively. Consider-

ing one module in row i and column j of the DMC,

i j

denotes one pixel in row k and column l of the

module. y

stands for one pixel in the reference mod-

ule. The reference module is generated based on an

averaging of all modules that belong to the DMC’s

ﬁnder-pattern and represent a binary one. ¯y and ¯x

i j

are the means of all the pixels referring to the refer-

ence module and the module in row i and column j of

the DMC, respectively.

3 DESIGN OF THE DECODER

The choice of an appropriate channel-model is es-

sential for the decoding success of the new designed



Tanner-

graph



= $



+ $



LDPC-based DMC

Figure 2: Symbol placement.

LDPC-based DMC. The channel-model has a high

impact on:

1. The design of the employed LDPC code;

2. The computation of the SDs passed to the LDPC

decoder;

3. The decoding procedure.

Therefore one has to study the DMC environment and

carefully choose an appropriate channel-model to rep-

resent everything in between the embossing and the

capturing of a DMC.

3.1 Channel-model in Absence of

Damages

In order to describe the distribution of the correlation-

coefﬁcients computed by equation (1), one has to

ﬁnd an appropriate channel-model. The correlation-

coefﬁcients are separated into two data-sets referring

to one-modules and zero-modules respectively. Then

one has to choose a Probability-Density-Function

(PDF) for each of the two data-sets that together de-

scribe the channel.

The distribution is mainly affected by the

embossing-technique, the material and the camera-

based system. Thus various pictures of DMCs milled

on different types of material like aluminum, copper,

steel, brass and different colored plastic have been

analyzed. Thereby several cutting depths have been

considered as well. Dependent on the material, the

acquisition of the codes was done in a bright or a dark

ﬁeld. This can be seen in the two examples in Fig-

ure 3. In Figure 3(a) the DMC was milled on a plate

of steel and the illumination setting caused the cavi-

ties to reﬂect the light directly into the camera’s lens.

Opposed to that the surface reﬂects the light into the

camera in Figure 3(b) where the DMC was milled into

a white plate of plastic.

The test of the null hypotheses that the one-

samples and the zero-samples belong to a Gaussian

distribution was done based on a 5% Shapiro-Wilk

(SW) test as well as a 5% Anderson-Darling (AD)

test. Only in a few cases the null hypotheses have

not been rejected. Furthermore this was only true for

ESTIMATION-DECODING ON LDPC-BASED 2D-BARCODES

(a) Dark ﬁeld (b) Bright ﬁeld

Figure 3: DMC milled on a) steel b) white plastic.

the zero-modules. Because of that, another analysis

was done by use of the Johnson distribution (Johnson,

1949) (Johnson et al., 1994) that provides a system

of curves with the ﬂexibility of covering a wide vari-

ety of shapes. Although the ﬁtting to lots of different

shaped samples works very good, the Gaussian ap-

proximation was chosen in the context of DMCs. The

reason for that is explained using the example of Fig-

ure 3(b) and the corresponding histograms shown in

Figure 4. Figure 4(a) shows the histogram of the zero-

modules and the one-modules of the DMC under the

situation of correct labeling of the modules. Accord-

ing to the employed SW-test and the AD-test the zero-

modules belong to a Gaussian-distribution whereas

the hypothesis for a Gaussian distribution of the one-

modules has been rejected. Thus the histogram of the

zero-modules on the left side in Figure 4(b) has been

approximated by a Gaussian curve whereas the curve

on the right side stems from a Johnson ﬁtting to the

histogram of the one-modules. It is well seen that the

two histograms as well as their ﬁtted curves overlap

each other.

In contrast to the above, the codeword is

not known when considering a common decoding-

process of a DMC. For the purpose of estimating the

PDF of the two types of modules we provisionally

separate the modules into two classes by applying a

threshold to the correlation coefﬁcients. The only dif-

ference between Figure 4(b) and Figure 4(c) is that

the ﬁtting curve to the histogram of the one-modules

in Figure 4(b) is obtained by a Johnson ﬁtting whereas

the approximation in Figure 4(c) has been done by us-

ing a Gaussian ﬁtting. The zero-samples have been

approximated by a Gaussian-PDF in both cases as

the hypothesis-test has been successful. As seen in

Figure 4(b), the approximation of the histogram with

the Johnson PDF leads to an overﬁtting. This sug-

gest a good conﬁdence for correlation values just be-

low the tentative threshold to belong to zero-modules.

In reality, this is not the case since the histograms of

the two classes heavily overlap. The suggested high

conﬁdence leads to large log-likelihood ratios (LLRs)

which are used in the subsequent decoding algorithm.

In this case the advantage of soft-decoding is lost.

Furthermore, when calculating the LLRs based on a

−0.4 −0.2 0 0.2 0.4 0.6 0.8

(a) Real distribution

−0.4 −0.2 0 0.2 0.4 0.6 0.8

(b) Fitted with Gauss & Johnson

−0.4 −0.2 0 0.2 0.4 0.6 0.8

Figure 4: Histograms of correlation-coefﬁcients separated

into one-modules and zero-modules.

Gaussian approximation, the histogram-skewness that

in many cases is responsible for the failure of the hy-

pothesis test, does not have a critical effect.

3.2 Channel-model for Damaged DMCs

The situation changes a lot when taking possible

damages into account. In industrial environment,

these are typically blots, scratches, dirt and rust as

well as effects caused by unequal illumination or

soiled camera-lenses. This leads to a change of the

gray-value distributions. In most cases one can ob-

serve a stretching of the histograms that refer to ones

and zeros respectively. Because of that a two-state

Markov-channel is utilized that includes possible ef-

fects caused by damages. The resulting channel-

model can be seen in Figure 5. The two states of the

Hidden-Markov Model (HMM) represent the follow-

ing two sub-channels:

Good Channel: This sub-channel is an Additive

White Gaussian Noise (AWGN) channel as described

in Section 3.1. This channel does not consider the

above mentioned damages and thus is referred to as

good channel.

Bad Channel: The second sub-channel is denoted as

bad channel and takes damages into account. It turns

out to be an AWGN channel as well, but with larger

variances compared to the good channel.

Thus the whole model represents a channel with

memory whose behavior is dependent on the current

underlying channel state. Moreover it is a Markov-

modulated Gaussian channel (MMGC) since it can be

SIGMAP 2011 - International Conference on Signal Processing and Multimedia Applications

 − 



Good

Channel

Bad

Channel





 − 

!!



!!

Figure 5: Channel-model based on a two-state hidden-

markov model.

16 vertical Markov-Chains

vertical Markov

Chains

16 horizontal Markov-Chains

16 horizontal Markov

Chains

Figure 6: Two-dimensional HMM.

described as a memoryless AWGN channel parame-

terized by the noise variances. The probabilities for

a transition from the good to the bad sub-channel and

vice versa are denoted as P

bad

and P

good

respectively.

3.3 ED2D-algorithm

The random-like connection of symbol-nodes with

check-nodes in a LDPC-code’s Tanner graph can

be interpreted as a build in interleaver. In tradi-

tional approaches channel interleavers are used to

obtain a channel which is assumed to be memory-

less. However, it has been shown (Wadayama, 2000)

(Garcia-Frias, 2004) (Ratzer, 2002) (Eckford, 2004)

that signiﬁcant improvement is obtained by use of an

Estimation-Decoding (ED) algorithm that takes the

channel’s memory into account.

The ED-algorithm is based on the so called

Markov-LDPC factor graph which comprises two

subgraphs, namely the LDPC code’s Tanner-graph

and the Markov chain. On the Markov-subgraph a

state-estimation is computed by use of the Forward-

Backward algorithm that is similar to the BCJR-

algorithm (Bahl et al., 1974). This algorithm is

bit-wise connected with the Belief-Propagation -

algorithm (BPA) (Gallager, 1962) on the LDPC-

subgraph to form the ED-algorithm. So far ED of

LDPC codes has only been applied to time dependent

and thus one-dimensional systems.

Considering the application of Estimation-

Decoding on DMCs the one-dimensional timescale

turns into a geometry of two dimensions. This leads

to a replacement of one Markov-chain by several

Markov-chains. In our Estimation-Decoding in two

dimensions (ED2D), we assign a sub-Markov-chain

to each row and each column of the DMC’s data

region as depicted in the example in Figure 6. This

way the state-estimation referring to a single module

is based on a horizontal Markov-chain and a vertical

Markov-chain. The complete 2D-Markov-LDPC

factor graph that the ED2D-algorithm is based on

is depicted in Figure 7 and the messages of one

sector are shown in Figure 8. For clarity purposes

only the messages for the horizontal Markov-chain

are depicted. r and c are the indices for the rows

and columns of the 2D-Markov-subgraph. The

check-nodes

and the symbol-nodes

are part of

the LDPC-subgraph whereas the state-nodes s and

the channel-nodes (black squares) belong to the

Markov-subgraph. The soft-decisions (SDs), that the

ED2D-algorithm receives from our image-processing

part (Section 2) are denoted by y. The noise added

to the binary value of a DMC-module in row r and

column c is assumed to stem either from the good

sub-channel or the bad sub-channel of the MMGC

which is dependent on the state that the state-node s

r,c

is estimated to be in. S = {G, B} is the set of states

a state-node s

r,c

can be in, where G and B represent

the good and the bad sub-channel respectively. The

forward and backward messages are represented

by α and β respectively. The channel-message ζ is

send from the 2D-Markov-subgraph to the LDPC-

subgraph. χ is the extrinsic information passed from

the LPDC-subgraph to the 2D-Markov-subgraph.

The messages of the 2D-Markov-subgraph are

computed as follows.

Forward-message α:

r,c+1

) =

∑

r,c

∈S

Pr(s

r,c+1

| s

r,c

)α

r,c

)

∑

r,c

∈{0,1}

Pr(x

r,c

| χ

r,c

)Pr(y

r,c

| x

r,c

, s

r,c

)

(2)

Backward-message β:

r,c

) =

∑

r,c+1

∈S

Pr(s

r,c+1

| s

r,c

)β

r,c+1

)

∑

r,c

∈{0,1}

Pr(x

r,c

| χ

r,c

)Pr(y

r,c

| x

r,c

, s

r,c

)

(3)

where Pr(s

r,c+1

| s

r,c

) is one of the four transition

probabilities of Figure 5. The computation of the

messages α

and β

for the vertical Markov-chains of

Figure 6 are likewise. The channel-message ζ passed

to the LDPC-subgraph is computed based on the mes-

ESTIMATION-DECODING ON LDPC-BASED 2D-BARCODES

Figure 7: 2D-Markov-LDPC factor graph.

sages α

and β

of the horizontal Markov-Chain and

the messages α

and β

of the vertical Markov-Chain:

r,c

=log

Pr(x

r,c

= 0 | α

r,c

)β

r,c+1

))

Pr(x

r,c

= 1 | α

r,c

)β

r,c+1

))

+log

Pr(x

r,c

= 0 | α

r,c

)β

r+1,c

))

Pr(x

r,c

= 1 | α

r,c

)β

r+1,c

))

(4)

with

Pr(x

r,c

= 0 | α

r,c

), β

r,c+1

)) =

∑

r,c

∈S

∑

r,c+1

∈S

Pr(y

r,c

| x

r,c

= 0, s

r,c

)

· Pr(s

r,c+1

| s

r,c

)α

r,c

)β

r,c+1

)

(5)

h and v refer to horizontal and vertical rows respec-

tively. Concerning the application of the ED2D-

algorithm in the context of DMCs, the DMC’s ﬁnder-

pattern offers another advantage next to the original

purpose. Since the values of the ﬁnder-pattern are al-

ways known, the corresponding messages χ do not

change during the iterative ED2D-decoding so that

Pr(x

r,c

| χ

r,c

) =

{

0 , x

r,c

= 0

1 , x

r,c

= 1

∀x

r,c

∈ F

(6a)

and

Pr(x

r,c

| χ

r,c

) =

{

1 , x

r,c

= 0

0 , x

r,c

= 1

∀x

r,c

∈ F

(6b)

with F

={one-modules of the ﬁnder-pattern} and

={zero-modules of the ﬁnder-pattern}. The

channel-message ζ and the extrinsic message χ re-

present the interface from the 2D-Markov-subgraph

to the LDPC codes Tanner-graph on which the mes-

sages are computed based on a common BPA (Gal-

lager, 1962).



,



,

,#$

,

,#$

,

(

,

)

,

,

(

LDPC –

subgraph

Markov –

subgraph

Horizontal

Markov-Chain

Figure 8: Local messages in the 2D-Markov-LDPC factor

graph.

4 IMPLEMENTATION & TEST

The ED2D-algorithm has been tested based on a

DMC of size 26 × 26. The data has been encoded

with a rate 0.61 regular PEG-LDPC code of length

n = 576. The ﬁnder-pattern that surrounds the 24 ×24

size data region and the code rate referring to the

DMC size have been chosen conforming to standard

(ISO/IEC, 2000). The 576 bits of the LDPC codeword

have been placed in the data region using the opti-

mization technique described in (Proßet al., 2010).

For comparison purposes the new designed

LDPC-based DMC and the original RS-based version

have been milled one next to the other on three differ-

ent kinds of material. For both versions, the informa-

tion to be encoded, the DMC-size and the code rate

have been chosen identically. In addition, the condi-

tions of the following acquisition and image process-

ing were exactly the same for all DMC-pairs. To in-

clude possible damages, a simulation of water drops

and oil drops was integrated. The simulation en-

sured that both versions of the DMC were interfered

with identical damages. An example of the damage-

simulation can be seen in Figure 9. For this test plates

of brass, aluminum and grey plastic have been used.

Each DMC was interfered with 10 simulated versions

of oil drops and water drops respectively. Thus, for

each material there have been two DMC versions pair-

wise interfered with 20 different disturbances. All in

all 60 interfered LDPC-based DMCs were compared

with 60 RS-based DMCs affected by exactly the same

damages.

The test results are shown in Figure 10. Success-

ful decodings are counted according to the material

and the type of damages. The last line shows the cu-

mulative percentage of succeeded decodings. With a

success rate of 92% our LDPC-based DMC decoded

with the ED2D-decoder clearly outperforms the stan-

dard DMC of which only 53% succeeded in decoding.

SIGMAP 2011 - International Conference on Signal Processing and Multimedia Applications

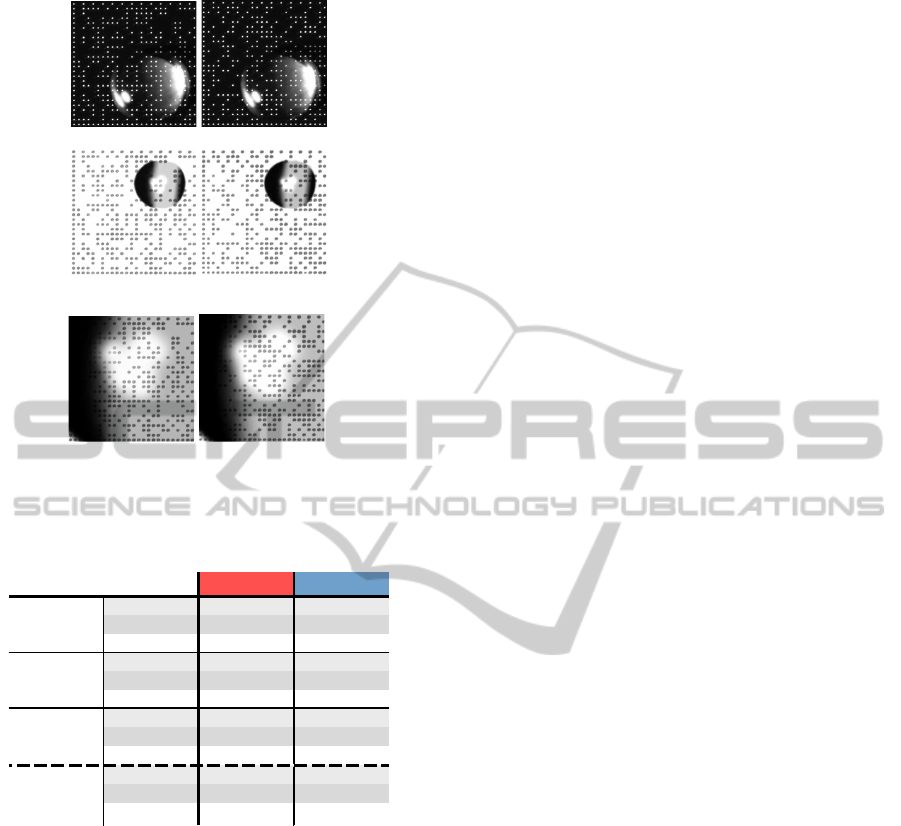
(a) LDPC DMC (b) Original DMC

(e) LDPC DMC (f) original DMC

Figure 9: DMC-pairs milled on the same plate of brass

and interfered with simulated water drop (a and b) and alu-

minum and interfered with simulated oil drop of size larger

than the DMC (c, d, e and f).

ED2D RS

water 9 4

oil 8 4

total 17 8

water 10 7

oil 10 10

total 20 17

water 10 4

oil 8 3

total 18 7

water 97% 50%

oil 87% 57%

Total 92% 53%

Plastic

Total

Successfully decoded

Aluminum

Brass

Figure 10: comparison results of 60 tests.

5 CONCLUSIONS

For the decoding of LDPC-based DMCs an algo-

rithm called ED2D-algorithm was established. This

decoding-algorithm is an extension of the one-

dimensional ED-algorithm. ED2D-decoding is based

on a two-dimensional Hidden-Markov-Model that has

been constructed in order to include possible dam-

ages into the underlying channel-model. Two types

of damages that are typical in industrial environment

were simulated. Based on the damage-simulation

a testing showed a superior decoding behavior of

our LDPC-based DMCs decoded with the ED2D-

algorithm compared to the standard RS-based DMC.

ACKNOWLEDGEMENTS

This work is part of the project MERSES and has been

supported by the European Union through its Euro-

pean regional development fund(ERDF) and by the

German state Baden-W

urttemberg. We would like to

thank the reviewers for helpful comments.

REFERENCES

Bahl, L. R., Cocke, J., Jelinek, F., and Raviv, J. (1974). Op-

timal decoding of linear codes for minimizing symbol

error rate. IEEE Transactions on Information Theory,

20(2):284–287.

Eckford, A. W. (2004). Low-density parity-check codes for

Gilbert-Elliott and Markov-modulated channels. PhD

thesis, University of Toronto.

Gallager, R. G. (1962). Low density parity check codes.

IRE Transactions on Information Theory, 1:21–28.

Garcia-Frias, J. (2004). Decoding of low-density parity-

check codes over ﬁnite-state binary markov channels.

IEEE Transactions on Communications, 52(11):1841.

Hu, X. Y., Eleftheriou, E., and Arnold, D. M. (2005).

Regular and irregular progressive edge-growth tanner

graphs. IEEE Transactions on Information Theory,

51(1):386–398.

ISO/IEC (2000). 16022:2000(e) information technology —

international symbology speciﬁcation — data matrix.

Johnson, N. L. (1949). Systems of frequency curves gen-

erated by methods of translation. Biometrika,36(1-

2):149.

Johnson, N. L., Kotz, S., and Balakrishnan, N. (1994). Con-

tinuous univariate distributions. A Wiley-Interscience

publication. Wiley, New York, 2. ed. edition.

MacKay, D. and Neal, R. (1995). Good codes based on very

sparse matrices. Cryptography and Coding, pages

100–111.

Proß, W., Quint, F., and Otesteanu, M. (2010). Using peg-

ldpc codes for object identiﬁcation. In Electronics and

Telecommunications (ISETC), 2010 9

, pages 361-

364.

Ratzer, E. A., editor (2002). Low-density parity-check codes

on Markov channels, Proceedings of 2nd IMA Con-

ference on Mathematics and Communications, Lan-

caster, U.K.

Tanner, R. M. (1981). A recursive approach to low com-

plexity codes. IEEE Transactions on Information The-

ory, 27:533–547.

Wadayama, T., editor (2000). An iterative decoding algo-

rithm of low density parity check codes for hidden

Markov noise channels, Proceedings of International

Symposium on Information Theory and Its Applica-

tions, Honolulu, Hawaii, USA.

Woodland, J. N. and Silver, B. (1949). U.S. Patent No.

2,612,994. Washington, DC: U.S. Patent and Trade-

mark Ofﬁce.

ESTIMATION-DECODING ON LDPC-BASED 2D-BARCODES