BUILDING VISUAL MAPS WITH A SINGLE OMNIDIRECTIONAL

CAMERA

Arturo Gil, David Valiente, Oscar Reinoso, Lorenzo Fern´andez and J. M. Mar´ın

Departamento de Ingenier´ıa de Sistemas y Autom´atica, Miguel Hern´andez University

Avda. de la Universidad s/n, Alicante, Elche, Spain

Keywords:

SLAM, Visual SLAM, Omni-directional images.

Abstract:

This paper describes an approach to the Simultaneous Localization and Mapping (SLAM) problem using a

single omnidirectional camera. We consider that the robot is equipped with a catadioptric sensor and is able

to extract interest points from the images. In the approach, the map is represented by a set of omnidirectional

images and their positions. Each omnidirectional image has a set of interest points and visual descriptors

associated to it. When the robot captures an omnidirectional image it extracts interest points and ﬁnds corre-

spondences with the omnidirectional images stored in the map. If a sufﬁcient number of points are matched, a

translation and rotation can be computed between the images, thus allowing the localization of the robot with

respect to the images in the map. Typically, visual SLAM approaches concentrate on the estimation of a set of

visual landmarks, each one deﬁned by a 3D position and a visual descriptor. In contrast with these approaches,

the solution presented here simpliﬁes the computation of the map and allows for a compact representation of

the environment. We present results obtained in a simulated environment that validate the SLAM approach.

In addition, we present results obtained using real data that demonstrate the validity of the proposed solution.

1 INTRODUCTION

Many applications in the ﬁeld of mobile robots re-

quire the existence of a map that represents the en-

vironment. Thus, the construction of a map is a key

ability for an autonomous vehicle. In order to build

the map the robot must explore the environment to

gather data and compute a coherent map. Commonly,

the pose of the robot during the exploration process is

unknown, leading to the problem of Simultaneous Lo-

calization and Mapping (SLAM). In these situations,

the robot needs to build a map incrementally, while,

simultaneously, computes its location inside the map.

To date, due to their precision, laser range sensors

have been used to build maps (Stachniss et al., 2004;

Montemerlo et al., 2002). Typically, these applica-

tions use directly the laser measurements to build 2D

occupancy grid maps (Stachniss et al., 2004), or they

extract features from the laser measurements (Monte-

merlo et al., 2002) to build 2D landmark-based maps.

During the last years, a great number of ap-

proaches propose the utilisation of cameras as the

main sensor in SLAM. These applications are usually

denoted as visual SLAM. Compared to laser ranging

systems, cameras are typically less expensiveand pro-

vide a huge quantity of 3D information (projected on

a 2D image), whereas typical laser range systems al-

low to collect distance measurements only on a 2D

plane. However, vision sensors are generaly less pre-

cise than laser sensors and require a signiﬁcant com-

putational effort in order to ﬁnd usable information

for the SLAM process.

Different approaches to SLAM using vision sen-

sors have been classiﬁed under the name of visual

SLAM. In these group, we can ﬁnd stereo-based ap-

proaches in which two calibrated cameras are used to

build a 3D map of the environment, which is repre-

sented by a set of visual landmarks referred to a com-

mon system, being each landmark accompanied by

a visual descriptor computed from its visual appear-

ance. Other approaches use a single camera to build

a map of the environment. For example in (Civera

et al., 2008) a single camera is used to build a 3D

map of the environment of visual landmarks extracted

with the Harris corner detector (Harris and Stephens,

1988). The camera is moved by hand. When viewed

from different viewpoints separated with a sufﬁcient

baseline, the 3D position of the landmarks can be es-

timated. The trajectory of the camera and the position

145

Gil A., Valiente D., Reinoso O., Fernández L. and M. Marín J..

BUILDING VISUAL MAPS WITH A SINGLE OMNIDIRECTIONAL CAMERA.

DOI: 10.5220/0003459701450154

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 145-154

ISBN: 978-989-8425-75-1

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

of the landmarks can be estimated up to a scale factor.

The performance of the single-camera SLAM is im-

proved when using a wide ﬁeld of view lens (Andrew

J. Davison et al., 2004), which suggests that using

an omni-directional camera would be advantageous

in visual SLAM, since the horizontal ﬁeld of view is

maximum.

We consider the case in which a mobile robot is

equipped with a single omni-directional camera, as

shown in Figure 1(a). Each image is processed to ex-

tract interest points that can be matched from differ-

ent viewpoints. We consider that the robot captures

an omnidirectional image. Next, the robot moves and

captures a different omnidirectional image. If we as-

sume that a set of signiﬁcant points can be extracted

and matched in both images, the relative movement

between the images can be computed (Scaramuzza

et al., 2009). In particular, the rotation between im-

ages can be univoquely computed, as well as the

translation (up to a scale factor). To obtain these

measurements between images we rely on a modiﬁca-

tion of the Seven Point Algorithm (Scaramuzza et al.,

2009). In Figure 1(b) we present two omnidirectional

images, where some correspondences have been in-

dicated. The transformation between both reference

systems is shown. In the experiments we rely on the

SURF features for the detection and description of the

points. In the SLAM infrastructure presented here,

the image I

will be named a view, in order to differ-

entiate from the commonly used visual landmarks. In

this sense, a view is an image captured from a pose

in the environment that is associated with a set of bi-

dimensional points extracted from it. It is worth not-

ing that a visual landmark corresponds to a physical

point, such as a corner on a wall. However, the view

represents the visual information that is obtained from

a particular pose in the environment.

In this paper we propose a different representa-

tion of the environment in the visual SLAM problem.

Instead of estimating the position of a set of visual

landmarks in the environment we consider the posi-

tion and orientation of a set of views in the environ-

ment. When the robot moves in the neighbourhood of

the view and captures an image with the camera, a set

of interest points will be matched between the current

image and the view, thus allowing to localize the robot

with respect to it. When the robot moves away from

the image, the appearance of the scene will vary and it

may be difﬁcult to ﬁnd corresponding points. In this

case, a new view will be created at the currentposition

of the robot with an uncertainty. The new view will al-

low the localization of the robot around its neighbour-

hood. It is worth noting that this representation has

been previously used in the context of localization.

(a)

(b)

Figure 1: Figure 1(a) shows the sensor setup used during the

experiments. Figure 1(b) presents two real omnidirectional

images acquired, with some correspondences indicated.

For example, in (Fernandez et al., 2010) a set of om-

nidirectional images acquired at certain points in the

environment are used to localize the environment us-

ing a Monte-Carlo algorithm and a global appearance-

based comparison of the images. In (Konolige et al.,

2010) a view-based map is proposed. Connections

between different stereo views are formed by consis-

tent geometric matching of their features. The map is

estimated with a graph optimization technique. How-

ever, in the approach presented here, an omnidirec-

tional camera is used instead, which allows us to rep-

resent the environment with a low number of omni-

directional images. In addition, the transformation

between views can only be computed up to a scale

factor, thus the restrictions between views cannot be

geometric.

The approach proposed in this paper presents

some advantages over previous visual SLAM ap-

proaches. The most important is the compactness of

the representation of the environment. For example,

in (AndrewJ. Davison et al., 2004; Civera et al., 2008)

an Extended Kalman Filter (EKF) is used to estimate

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

146

the position of the visual landmarks, as well as the po-

sition and orientation of the camera. In (Civera et al.,

2008) 6 variables are used to represent each landmark,

thus the state vector in the EKF grows rapidly with

the number of landmarks in the environment. This

fact poses a challenge for most existing SLAM ap-

proaches. In opposition with these, in the algorithm

presented here, only the pose of a reduced set of views

is estimated. Thus, each view encapsulates informa-

tion of a particular area in the environment, in the

form of several interest points detected in the image.

Typically, as will be shown in the experiments, a sin-

gle view may retain a sufﬁcient number of interest

points so that the localization in its neighbourhood

can be performed.

The main disadvantage of the presented approach,

is, nevertheless, the computational cost of determin-

ing a metric transformation between two omnidirec-

tional images. However, in Section 4 we present an

algorithm that can be used to process images at a fast

rate and can be used for online SLAM. In this case,

the computation of the transformation between two

images depends only on the number of matches, that

can be easily adjusted to provide both speed and pre-

cise results.

We present a series of results obtained in simula-

tion and with real omnidirectionalimages that demon-

strate the validity of the approach. We ﬁrst compute

a gaussian observation noise model for the measure-

ments between images. Based on this model, we

present a series of experiments in a simulated envi-

ronment. Finally, we present results using real images

captured in an ofﬁce-like environment.

The rest of the paper is organized as follows. First,

Section 2 presents some related work in the ﬁeld of vi-

sual SLAM. Next, Section 3 describes the SLAM pro-

cess in this kind of architecture. The algorithm used

to estimate the transformation between two omnidi-

rectional images is described in Section 4. Finally,

Section 5 presents experimental results.

2 RELATED WORK

We can classify the different visual SLAM ap-

proaches with respect to:

• The sensor used, mainly: stereo cameras, a single

camera or omnidirectional camera.

• The detection of signiﬁcant points or regions: that

is the method used to extract robust points that

can be matched accross images. For example the

Harris corner detector has been extensively used

in the visual SLAM ﬁeld (Davison and Murray,

2002; Gil et al., 2010b).

• The visual description of the points: the visual

landmarks are commonly described in order to

be distinguished and associated in the map. The

SIFT (Lowe, 2004) and SURF (Bay et al., 2006)

have been used extensivelyin the contextof visual

SLAM.

• The representation of the map: commonly the

map is represented by a set of visual landmarks.

Each visual landmark is a point-feature in the en-

vironment that can be easily detected in the im-

ages. In the map, each landmark is stored as a 3D

position along with a visual descriptor, partially

invariant to view changes.

• The SLAM algorithm: such as an EKF-based ap-

proach, Rao-Blackwellized particle ﬁlters, etc.

For example, in (Se et al., 2001) stereo vision is

used to extract 3D visual landmarks from the envi-

ronment. During exploration, the robot extracts SIFT

features from stereo images and calculates relative

measurements to them. Landmarks are then inte-

grated in the map with a Kalman Filter associated to

each one. In (Gil et al., 2006) a Rao-Blackwellized

particle ﬁlter is used to estimate simultaneously the

map and the path of a single robot exploring the envi-

ronment. A single low-cost camera is used in (Davi-

son and Murray, 2002) to estimate a map of 3D visual

landmarks and the 6 DOF trajectory of the camera

with an EKF-SLAM algorithm. The interest points

are detected with the Harris corner detector (Harris

and Stephens, 1988) and described with a grey level

patch. Since distance cannot be measured directly

with a single camera, the initialization of the XYZ

coordinates of a landmark poses a problem. This fact

inspired the inverse depth parametrization exposed

in (Civera et al., 2008). A variation of the Information

Filter is used in (Joly and Rives, 2010) to estimate a

visual map using a single omnidirectional camera and

an inverse depth parametrization of the landmarks.

Finally, in (Jae-Hean and Myung Jin, 2003) two om-

nidirectional cameras are combined to obtain a wide

ﬁeld of view stereo vision sensor. In (Scaramuzza

et al., 2009), the computation of the essential matrix

between two views allows to extract the relative mo-

tion between two camera poses, which leads to a vi-

sual odometry.

3 SLAM

In this section we describe in detail the representa-

tion of the environment as well as the creation of the

map. The visual SLAM problem is solved in a dual

manner. Instead of estimating the position of a set of

BUILDING VISUAL MAPS WITH A SINGLE OMNIDIRECTIONAL CAMERA

147

visual landmarks, we propose the estimation of the

position and orientation of a set of views obtained

from the environment. Thus, the map is formed by

a set of omnidirectional images obtained from differ-

ent positions in the environment. In opposition with

other solutions, the landmarks do not correspond to

any physical element in the environment (e.g. a cor-

ner, or the trunk of a tree). In our case, a landmark

(renamed view) will be constituted by an omnidirec-

tional image captured at the pose x

= (x

,θ

) and

a set of interest points extracted from that image.

In our opinion, the SLAM architecture presented

in this paper is suitable for different kind of SLAM al-

gorithms, online methods such as, EKF, FastSLAM or

ofﬂine, such as, for example, Stochastic Gradient De-

scent (Grisetti et al., 2007). In this paper we present

the application of the EKF to the map representation

proposed and show how to obtain correct results using

real data.

In addition we consider that the map representa-

tion and the measurement model can be also be ap-

plied using standard cameras. The reason for using

omnidirectional images is their ability to acquire a

global view of the environment in a single image.

3.1 Map Representation

We propose the estimation of the pose x

,θ

)

of a mobile robot at each time t as well as

the pose of N views. Each view i is constituted by its

pose x

= (x

,θ

)

, its uncertainty P

and a set of

M interest points p

expressed in image coordinates.

Each point is associated with a visual descriptor d

j = 1, . . . , M.

This map representation is shown in Figure 2,

where the position of several views is indicated. For

example, the view A is stored with a particular pose

= (x

,θ

)

in the map and has a set of M

points detected in it. The view A allows the localiza-

tion of the robot in the corridor. The view B represents

the ﬁrst room, whereas the viewC represents a second

room 2, and allows the robot to localize in it.

The augmented state vector is thus deﬁned as:

x =







···







(1)

where N is the number of views that exist in the map.

3.2 Map Building Process

We present an example of map building in an ofﬁce-

like indoor environment, also described in Figure 2.

Figure 2: The ﬁgure presents the basic idea in map cre-

ation. The robot starts the exploration from the point A and

stores a view I

at the origin. Next, the robot moves. When

no matches are found between the current image and I

, a

new view is created at the current position of the robot B.

The process continues until the whole environment is rep-

resented

We consider that the robot starts the exploration at

the origin denoted as A, placed at the corridor. At

this point, the robot captures an omnidirectional im-

age I

, that will be used as a view. We assume that,

when the robot moves inside the corridor, several cor-

respondences can be found between I

and the current

omni-directional image. When the robot enters the

ﬁrst room, the appearance of the images vary signif-

icantly, thus, no matches are found between the cur-

rent image and image I

. In this case, the robot will

initiate a new view named I

at the current robot posi-

tion. Finally, the robot goes into a different room and

creates a new view named I

3.3 Observation Model

In the following we describe the observation model

proposed. We assume that there exist two omnidi-

rectional images obtained from two different poses in

the environment. One of the images is stored in the

map and the other is the current image captured by

the robot. We assume that given two images we are

able to extract a set of signiﬁcant points in both im-

ages and obtain a set of correspondences. Next, as

will be described in Section 4, we are able to obtain

the observation z





arctan(

−y

−x

) − θ

− θ

(2)

where the angle φ is the bearing at which the view

n is observed and β is the relative orientation be-

tween the images. The landmark n is represented by

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

148

= (x

,θ

), whereas the pose of the robot is de-

scribed as x

= (x

,θ

). Both measurements (φ, β)

are represented in Figure 1(a).

3.4 New View Initialization

A new omnidirectional image is included in the map

when the number of matches found in the neighbour-

ing views is low. In particular, we use the following

ratio:

R =

+ n

(3)

that computes the similarity between views A and B,

being m the total number of matches between A and B

and n

the number of detected points in images

A and B respectively. The robot decides to include

a new view in the map whenever the ratio R drops

below a pre-deﬁned threshold. In order to initialize a

new view, the pose of the view is obtained from the

current estimation of the robot pose. The uncertainty

in the pose of the landmark equals in this case the

uncertainty in the pose of the robot.

3.5 Data Association

The data association problem in a feature-based

SLAM algorithm can be posed in the following way:

given a set of observations z

= {z

t,1

t,2

,... , z

t,B

} ob-

tained at time t, compute the landmarks in the map

that generated those observations. Thus, the result

of the data association is a vector of B indexes H =

{ j

, j

,... , j

}, where each index j

∈ [1,N + 1] de-

notes one of the landmarks in the map, being N the

total number of landmarks. If the observation z

t,i

does not correspond to any of the landmarks in the

map, a new one is initialized with index N + 1. Find-

ing the correct data associations is crucial in SLAM,

since false data associations may cause the SLAM ﬁl-

ter to diverge. Finding the correct data association

can be complex if the landmarks are close together

and this fact has inspired solutions such as the Joint

Compatibility Test (Neira and Tard´os, 2001). In the

approach presented here the data association process

can be tackled in a more simple way. Consider, for

example, that at time t the robot captures an omnidi-

rectional image I

and extracts a set of interest points.

To ﬁnd the data association, we proceed in the follow-

ing way: First, we select a subset of candidate views

from the map. The selection is based on the Euclidean

distance:

− x

)

· (x

− x

). (4)

The view i is included in the candidate set if D

< δ,

where δ is a pre-deﬁned threshold. Higher values of δ

allow the loop closure with a higher accumulated er-

ror in the pose, but need a higher computational cost.

Next, we look for a set of matching points between the

current image I

and each of the images in the candi-

date set {I

,... , I

}. We can compute an observa-

tion z

= (φ, β) to any of the images in the candidate

set if the number of matches is sufﬁcient. As will be

explained in Section 4 we are able to compute an ob-

servation with only 4 matches. However, in practice,

we require a higher number of matches in order to re-

ject false correspondences. In addition, we compute

the ratio R deﬁned in Equation 3 and initialize a new

view whenever this ratio goes below 0.5.

4 TRANSFORMATION BETWEEN

OMNI-DIRECTIONAL IMAGES

In this section we present a method to obtain the rel-

ative angles β and φ between two omni-directional

images, as represented in Figure 1(b). These angles

reveal the relative pose of the robot and allow for its

localization. This poses the problem of detecting fea-

ture points in both images and ﬁnding the correspon-

dences between images in order to recover a certain

camera rotation and translation by applying epipolar

constains. Traditional schemes, such as (Kawanishi

et al., 2008; Nister, 2003; Stewenius et al., 2006)

solve the problem in the general 6 DOF case, whereas

in our case, according to the speciﬁc motion of the

robot on a plane, we are able to reduce it to 4 vari-

ables, thus the resolution is simpliﬁed in terms of

computational cost. The obtention of the relative an-

gles between two poses of the robot takes approxi-

mately t = 0.4msec, which conﬁrms the capability to

work in real-time.

4.1 Signiﬁcant Point Detection and

Matching

We are using SURF features (Bay et al., 2006) in or-

der to ﬁnd interest points in the images. According

to (Gil et al., 2010a), SURF features are able to out-

perform other detectors and descriptors in terms of

robustness of the detected points and invariance of

the descriptor. Moreover in (Murillo et al., 2007)

SURF points detection succeed with omnidirectional

images. We transform the omnidirectional images

into a panoramic view in order to increase the num-

ber of valid matches between images due to the lower

appearance variation obtained with this view. The

method to obtain robust correspondences of SURF

points across images has been based on keypoint

BUILDING VISUAL MAPS WITH A SINGLE OMNIDIRECTIONAL CAMERA

149

matching ratios reported in (Lowe, 2004). Then, the

process is inverted to recover the coordinates into the

original omnidirectional view.

4.2 Computing the Transformation

Once SURF points are detected and matched in two

images it appears the necessity to establish a process

to retrieve relative angles β and φ.

4.2.1 Epipolar Geometry

The epipolar condition stablishes the relationship be-

tween two 3D points seen from different views.

′T

Ep = 0 (5)

where the matrix E is denoted as the essential ma-

trix and can be computed from a set of corresponding

points in two images. The same point detected in two

images can be expressed as p = [x, y,z]

in the ﬁrst

camera reference system and p

′

= [x

′

]

in the

second camera reference system. In our case, since

only one camera is employed, images are taken from

two unknown poses without knowledge about the dis-

tance between them. This fact leads to a lack of depth

information, and the solution can only be recovered

up to a scale factor ρ. In addition, essential matrix

E, represents a speciﬁc rotation R and a translation T

(up to a scale factor) between the two image reference

systems, with E = R· T

. Thus the desired angles can

be recovered from the decomposition of E. Please

note that Epipolar Geometry can be used with omni-

directional images since we back-project 2D image-

plane system to 3D using a modelled hyperbolic cam-

era’s mirror, which is provided by means of a previous

calibration step (Scaramuzza et al., 2006). Because of

the depth ambiguity, we denote ~p and

′

in 3D, as the

unitary vectors that indicate the direction of the points

in the two reference systems, since the 3D position

cannot be completely deﬁned with only one view of

the scene.

To accomplish the objective of obtaining β and φ,

we have considered the approach (Hartley and Zis-

serman, 2004) which suggests retrieving directly the

projection matrix P, that also deﬁnes the transforma-

tion between images. This method has been adopted,

since it provides a simple way to compute the four

possible solutions to the problem. First, we apply the

epipolarity constrain ~p

′T

· E · ~p = 0 to N points, and

solve the resulting Equation D· E = 0. Next we apply

SVD decomposition to E:

[U|S|V] = SVD(E) (6)

that allows to compute:

= [UV

W] (7)

= [UV

] (8)

T = [UZU

] (9)

being W and Z auxiliary matrices (Hartley and Zis-

serman, 2004) and both possible rotations (R

)

and translations (T

,−T

). To obtain the four pos-

sible P-matrices, we compute:

= [R

], P

= [R

| − T

= [R

], P

= [R

| − T

], (10)

In our case, the projection matrices have the fol-

lowing form:







cos(β) −sin(β) 0 ρcos(φ)

sin(β) cos(β 0 ρcos(φ)

0 0 1 0

0 0 0 1







(11)

Notice that β, φ and ρ may take different values that

satisfy the epipolar condition (5) due to the undeter-

mined scale factor ρ. This poses the problem of se-

lecting one of the four possible solutions described in

Equation (10), which will be detailed in the following

subsection.

4.2.2 Selecting a Solution

In order to ﬁnd the correct solution, an inverse pro-

cedure has to be carried out. We multiply

′

by the

inverse of the four projection matrixes P

, obtaining

four estimations of ~p. The less deviated one respect

to~p is assumed to have been obtained through the cor-

rect solution. Finally, β and φ are directly recovered

from the elements of P as deﬁned in Equation (11).

Since we are estimating a rotation and a transla-

tion of a planar motion on the XY plane, only N = 4

correspondences sufﬁce to solve the problem. It is

easy to show that the matrix E has only 4 non-zero

elements. However, in order to obtain a better so-

lution in the presence of noise and false correspon-

dences, we process more points in the computation

and use RANSAC for outlier rejection (Nist´er, 2005).

In particular, it is worth noticing that the SURF fea-

tures can be tuned to obtain a reduced set of highly

robust points. In consequence, we obtain a reduced

set of matches, thus leading to a fast computational

time.

5 RESULTS

We present three diferent experimental sets. First,

in Section 5.1 we present results obtained in simula-

tion that validate the SLAM approach proposed here.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

150

Next, Section 5.2 presents the results using real data

captured with a Pioneer P3-AT indoor robot. The

robot is equipped with a ﬁrewire 1280x960 camera

and a hyperbolic mirror. The optical axis of the cam-

era is installed approximately perpendicular to the

ground plane, as described in Figure 1(a), in conse-

quence, a rotation of the robot corresponds to a rota-

tion of the image with respect to its central point. In

addition, we used a SICK LMS range ﬁnder in order

to compute a ground truth using the method presented

in (Stachniss et al., 2004).

5.1 SLAM Results in Simulation

We performed a series of experiments in simulation

in order to test the suitability of the proposed SLAM

scheme. Please note the importance of assuring the

convergenceof an EKF-based SLAM algorithm when

a new observation model is introduced. Figure 3(a)

presents the simulation environment 1. The true path

followed by the robot is shown with continuous line,

whereas the odometry is represented in dashed line.

A set of views have been placed randomly along the

trajectory and shown with a dot. Please note that the

placement of the views depends of the appearance of

the images and the ratio R selected. In the simulation

we have placed the views randomly with distances

similar to the real case.

The robot starts the SLAM process at the origin

and performs two turns along the trajectory. The

range, i.e. the capability of computing the observation

= (φ, β)

at a given distance is shown with a dash-

dotted line. The observations obtained by the robot

have been simulated using the observation model pre-

sented in Equation 2 with an added gaussian noise

with σ

= σ

= 0.1rad. Figure 3(b) presents the sim-

ulation environment 2, which emulates a typical in-

door environment, where the computation of the ob-

servations is restricted by the walls. We performed

a series of experiments when varying the range of

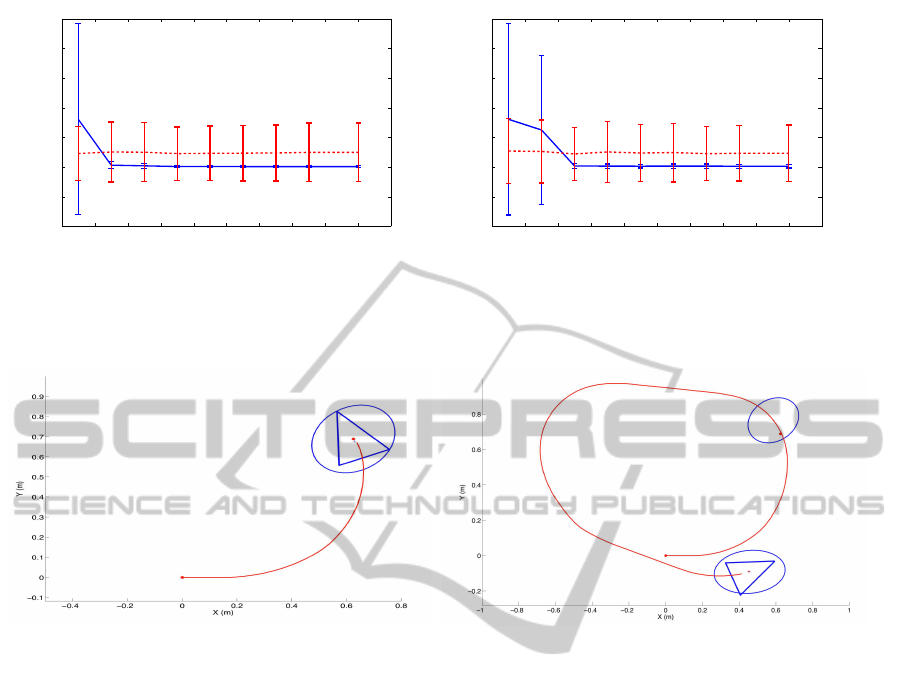
the observed views. The results are presented in Fig-

ure 4(a) and 4(b), where we present the RMS error in

the trajectory when the range of the sensor is varied.

We compare the EKF solution (continuous line) to the

odometry (dashed line) when compared to the laser-

based ground-truth. We generated different odometry

sets randomly and repeated the experiment 50 times.

In Figure 4(a) we present the mean and 2σ intervals.

As can be observed in Figure 4(a) when the range is

0.5m the uncertainty in the pose grows without bound

and the ﬁlter is not able to converge. It can be ob-

served that the RMS error decreases when the sensor

range goes beyond 3m. A similar result is presented

in Figure 4(b), which corresponds to the simulation

environment 2. In this case, nice results are obtained

when the range is over 9m, since the walls restrict the

visibility of the views an makes the convergence of

the ﬁlter more difﬁcult. Please note that the results

depend strongly on the placement of the views, plac-

ing more viewsallows to compute a more precise map

and trajectory, however it requires a higher computa-

tional cost.

−5 0 5 10 15 20 25

−5

X (m)

Y (m)

(a)

−5 0 5 10 15 20

X (m)

Y (m)

(b)

Figure 3: Figure 3(a) represents the simulation environment

1. The location of the different views in the map is repre-

sented by dots. Figure 3(b) presents the simulation environ-

ment 2.

5.2 SLAM with Real Data

In this section we present SLAM results that val-

idate the approach presented here. The robot is

guided through the environment and captures omnidi-

rectional images along the trajectory and laser range

data. Again, in order to compare the results, we use a

laser-based SLAM algorithm, as described in (Stach-

niss et al., 2004). The robot starts by initializing an

omnidirectional image at the origin, as indicated in

Figure 5(a). Next, it starts to move along the trayec-

tory while capturing omnidirectional images. A new

view is initialized a few steps later, as indicated in

Figure 5(a) with an error ellipse. While mapping, the

current image is compared with the rest of the views

in the map, and a set of correspondences is found. In

BUILDING VISUAL MAPS WITH A SINGLE OMNIDIRECTIONAL CAMERA

151

4 6 8 10 12 14 16 18 20 22 24

−20

−10

RMS error in position vs. sensor range

RMS error xy (m)

Sensor range (m)

(a)

4 6 8 10 12 14 16 18 20 22 24

−10

−5

RMS error in position vs. sensor range

RMS error xy (m)

Sensor range (m)

(b)

Figure 4: Figure 4(a) presents the results obtained in the simulation environment 1. Figure 4(b) presents the results obtained

in the simulation environment 2.

(a) (b)

Figure 5: Figure 5(a) and 5(b) present two initial steps in the creation of the map shown in Figure 6.

addition, the similarity ratio (3) is computed. When-

ever the similarity of the current image drops below

= 0.5 a new view is created and initialized at the

current robot position. In Figure 5(b) we present the

occurrence of this event, where a third view is initial-

ized. Finally, the robot performs the trajectory shown

in Figure 6(a), where we show with dots the rest of the

poses where the robot decided to initialize a new im-

age. We present with a dashed line the ground truth,

whereas the EKF estimation is drawn with continu-

ous line. The odometry is represented with a dash-

dotted line. It is worth noting that the robot continues

to move inside the same room and is able to compute

observations of the views initialized before. In our

case, the threshold δ

was selected experimentally in

order to have a reduced set of views that represent the

environment in a compact manner. If a lower δ

selected, less images are initialized in the map. On

the contrary, if a greater value of δ

is selected (i.e.

0.9), the ﬁnal map will have a large number of views.

As can be seen in Figure 6(a) once the fourth view is

initialized, no more views are initialized, thus leading

to a compact representation of this environment. In

Figure 6(b) we compare the estimated trajectory with

the ground truth and the odometry at every step of the

trajectory. We present the error in the estimated tra-

jectory (dashed line) with 2σ interval and the error in

the odometry (dash-dotted line).

Figure 7 presents another experiment. In this case,

the robot explores a room, travels through a corri-

dor, goes into a different room and returns. The to-

tal traversed distance is 45m. Figure 7(a) presents

the ground-truth trajectory (dashed line), the odom-

etry (dash-dotted line) and the estimation (continuous

line). The location of the views and its associated un-

certainty is indicated with error ellipses. On Figure

7(b) we present the error in the pose at every step of

the SLAM process with 2σ intervals.

6 CONCLUSIONS

We have presented and approach to the Simultaneous

Localization and Mapping (SLAM) problem using a

single omnidirectional camera. We propose a differ-

ent representation of the environment. Instead of es-

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

152

(a)

0 100 200 300 400 500 600 700 800 900

−1

Error in X (m)

0 100 200 300 400 500 600 700 800 900

−1

−0.5

0.5

Error in Y (m)

0 100 200 300 400 500 600 700 800 900

−1.5

−1

−0.5

0.5

Step

Error in θ (m)

(b)

Figure 6: Figure 6(a) presents the results of SLAM using real data with ground-truth (dashed), estimation (continuous) and

the odometry (dash-dotted). The position of the views is presented with error ellipses. Figure 6(b) presents the error in X, Y

and θ at each time step of the estimation (dashed) and the odometry (dash-dotted).

(a)

0 200 400 600 800 1000 1200

−2

−1

Error in X (m)

0 200 400 600 800 1000 1200 1400

−2

−1

Error in Y (m)

0 200 400 600 800 1000 1200

−0.4

−0.2

0.2

0.4

Step number

Error in θ (rad)

(b)

Figure 7: Figure 7(a) presents the results of SLAM using real data with ground-truth (dashed), estimation (continuous) and

the odometry (dash-dotted). The position of the views is presented with error ellipses. Figure 7(b) presents the error in X, Y

and θ at each time step of the estimation (dashed) with a 2σ interval.

Figure 8: The ﬁgure presents the occupancy grid map cre-

ated during the experiment shown in Figure 7.

timating the 3D position of a set of visual landmarks

in the environment, we only estimate the position and

orientation of a set of omnidirectional images. Each

omnidirectional image has a set of interest points and

visual descriptors associated to it and describes in a

compact way the environment. Each omnidirectional

image allows the localization of the robot around its

neighbouring. Given two omnidirectional images and

a set of corresponding points, we are able to com-

pute the rotation and translation (up to a scale fac-

tor) between the images. This allows us to propose

an observation model and compute a map and a tra-

jectory. We present localization and SLAM results

using an EKF-based SLAM algorithm, however, we

consider that different SLAM strategies may be used.

We present results obtained in a simulated environ-

ment that validate the SLAM approach. In addition,

we have shown the validity of the approach by using

real data captured with a mobile robot.

BUILDING VISUAL MAPS WITH A SINGLE OMNIDIRECTIONAL CAMERA

153

REFERENCES

Andrew J. Davison, A. J., Gonzalez Cid, Y., and Kita, N.

(2004). Improving data association in vision-based

SLAM. In Proc. of IFAC/EURON, Lisboa, Portugal.

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). SURF:

Speeded up robust features. In Proc. of the ECCV,

Graz, Austria.

Civera, J., Davison, A. J., and Mart´ınez Montiel, J. M.

(2008). Inverse depth parametrization for monocular

slam. IEEE Trans. on Robotics.

Davison, A. J. and Murray, D. W. (2002). Simultaneous lo-

calisation and map-building using active vision. IEEE

Trans. on PAMI.

Fernandez, L., Gil, A., Paya, L., and Reinoso, O. (2010).

An evaluation of weighting methods for appearance-

based monte carlo localization using omnidirectional

images. In Proc. of the ICRA, Anchorage, Alaska.

Gil, A., Martinez-Mozos, O., Ballesta, M., and Reinoso, O.

(2010a). A comparative evaluation of interest point

detectors and local descriptors for visual slam. Ma-

chine Vision and Applications.

Gil, A., Reinoso, O., Ballesta, M., Juli´a, M., and Pay´a, L.

(2010b). Estimation of visual maps with a robot net-

work equipped with vision sensors. Sensors.

Gil, A., Reinoso, O., Martnez-Mozos, O., Stachniss, C., and

Burgard, W. (2006). Improving data association in

vision-based SLAM. In Proc. of the IROS, Beijing,

China.

Grisetti, G., Stachniss, C., Grzonka, S., and Burgard, W.

(2007). A tree parameterization for efﬁciently com-

puting maximum likelihood maps using gradient de-

scent. In Proc. of RSS, Atlanta, Georgia.

Harris, C. G. and Stephens, M. (1988). A combined corner

and edge detector. In Proc. of Alvey Vision Confer-

ence, Manchester, UK.

Hartley, R. and Zisserman, A. (2004). Multiple View Geom-

etry in Computer Vision. Cambridge University Press.

Jae-Hean, K. and Myung Jin, C. (2003). Slam with omni-

directional stereo vision sensor. In Proc. of the IROS,

Las Vegas (Nevada).

Joly, C. and Rives, P. (2010). Bearing-only SAM using a

minimal inverse depth parametrization. In Proc. of

ICINCO, Funchal, Madeira (Portugal).

Kawanishi, R., Yamashita, A., and Kaneko, T. (2008). Con-

struction of 3D environment model from an omni-

directional image sequence. In Proc. of the Asia Inter-

national Symposium on Mechatronics 2008, Sapporo,

Japan.

Konolige, K., Bowman, J., Chen, J., and Mihelich, P.

(2010). View-based maps. IJRR.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision.

Montemerlo, M., Thrun, S., Koller, D., and Wegbreit, B.

(2002). Fastslam: a factored solution to the simulta-

neous localization and mapping problem. In Proc. of

the 18th national conference on Artiﬁcial Intelligence,

Edmonton, Canada.

Murillo, A. C., Guerrero, J. J., and Sag¨u´es, C. (2007). SURF

features for efﬁcient robot localization with omnidi-

rectional images. In Proc. of the ICRA, San Diego,

USA.

Neira, J. and Tard´os, J. D. (2001). Data association in

stochastic mapping using the joint compatibility test.

IEEE Trans. on Robotics and Automation.

Nister, D. (2003). An efcient solution to the ﬁve-point rela-

tive pose problem. In Proc. of the IEEE CVPR, Madi-

son, USA.

Nist´er, D. (2005). Preemptive RANSAC for live structure

and motion estimation. Machine Vision and Applica-

tions.

Scaramuzza, D., Fraundorfer, F., and Siegwart, R. (2009).

Real-time monocular visual odometry for on-road ve-

hicles with 1-point RANSAC. In Proc. of the ICRA,

Kobe, Japan.

Scaramuzza, D., Martinelli, A., and Siegwart, R. (2006).

A toolbox for easily calibrating omnidirectional cam-

eras. In Proc. of the IROS, Beijing, China.

Se, S., Lowe, D., and Little, J. (2001). Vision-based mobile

robot localization and mapping using scale-invariant

features. In Proc. of the ICRA, Seoul, Korea.

Stachniss, C., Grisetti, G., Haehnel, D., and Burgard, W.

(2004). Improved Rao-Blackwellized mapping by

adaptive sampling and active loop-closure. In Proc.

of the SOAVE, Ilmenau, Germany.

Stewenius, H., Engels, C., and Nister, D. (2006). Recent de-

velopments on direct relative orientation. ISPRS Jour-

nal of Photogrammetry and Remote Sensing.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

154